宽温域下电静液作动器的液压缸活塞格莱圈动密封性能分析

韩小霞， 冯永保， 谢 建， 魏小玲， 李 良

(火箭军工程大学 导弹工程学院， 陕西 西安 710025)

引言

电静液作动器(Electro-hydrostatic Actuators，EHA)是典型的高度集成化和小型化电液控制系统， 其在减小体积和重量的同时，减小了散热面积，大大降低了自身散热能力，使得一部分热量滞留在EHA的密闭腔体内，从而导致EHA系统的油温快速上升[1-3]，影响运行安全。在实际应用中，EHA系统中液压油液的温度变化尤其明显，使得其主要部件液压缸的活塞密封结构的泄漏流量和启动摩擦力发生变化，从而导致EHA系统表现出变死区特性。

液压缸活塞密封件一般选用填料组合式动密封，即格莱圈密封。格莱圈是O形圈与方形圈的组合密封形式，方形圈材料为聚四氟乙烯，更加耐磨，与金属之间的摩擦力更低，方形圈弥补了O形圈不耐磨且摩擦力大的缺点，而橡胶O形圈具有高弹性，可自补偿方形圈的磨损[4]。密封件失效是高压高温电液控制系统产生故障的主要原因之一。在高温下密封件发生热膨胀，压缩应力显著提高，长时间暴露在高温之下，密封件发生永久变形，当温度保持不变时，密封件仍可起到密封作用，但当温度降低时，密封件很快收缩，脱离密封表面，产生泄漏，从而造成液压缸有效输出流量死区，影响EHA的控制性能。因此，研究宽温域下液压缸活塞格莱圈动密封性能对EHA的高精度控制具有实际意义。

针对填料密封圈已有不少研究，主要包括密封性能分析和结构参数优化。其中，针对O形密封圈的研究较多[5-11]：文献[5]分析了原油高温热采工具O形橡胶圈在高温高压下的密封性能，研究表明，当温度升高时O形圈最大接触应力和最大剪切应力均相应减小，而最大Von Mises应力明显减小；文献[6]为了定量计算高精度电液伺服马达的内泄漏，提出了一种基于有限元的油膜控制方程数值解法，并分析了O形圈预压缩量、介质压力、油温等参数对泄漏量和摩擦力的影响，研究结果表明，长时间高频工作状态下，电液伺服马达的泄漏量和摩擦力会随着温度的升高而降低，但密封的磨损量将会增加；文献[7]针对液压缸活塞杆O形圈密封结构，研究了摩擦热对O形圈密封性能的影响，结果表明，当密封接触面发热严重时，密封圈变软，密封间隙无法自补偿，使得油液泄漏量增加，密封性能下降。

文献[12]针对航空液压作动器中组合密封件，分析了不同压合量、温度和油压对泄漏量和摩擦力的影响，发现当温度升高时，泄漏量减小，但摩擦力增大；通过改变方形圈结构减小了泄漏量；文献[13]研究了格莱圈在不同O形圈压缩量和材料硬度、方形圈厚度下的动密封性能，并基于响应曲面法，以最大接触压力和最小启动摩擦力为优化目标，对格莱圈的密封参数进行了优化；文献[14]分析了组合密封件在偏置状态下的密封性能变化规律。综上分析，虽然已有大量关于格莱圈(组合密封圈)的研究，但对宽温域下液压缸活塞格莱圈密封性能研究较少。

本研究通过数值分析不同介质压力和温度时液压缸活塞格莱圈性能，获得密封接触面上的接触压力，利用逆解一维雷诺方程获得密封面间的油膜厚度，建立考虑油液黏温特性时最大启动压力和泄漏流量的数学模型，分析活塞单行程运行过程中最大启动压力和泄漏流量随介质压力和温度的变化规律，为EHA的液压缸活塞格莱圈的设计和选型提供参考。

1 模型建立

1.1 几何模型建立

图1所示为EHA组成及其液压缸活塞用格莱圈密封的几何模型。安装时的预压缩量决定着泄漏流量和启动压力的大小，密封结构及格莱圈参数如表1所示。

图1 液压缸活塞格莱圈密封结构几何模型

表1 几何模型参数

1.2 有限元计算模型

采用ABAQUS软件建立图1所示格莱圈的二维轴对称有限元模型。其中O形圈材料是硬度为邵氏70°的丁腈橡胶，方形圈材料为聚四氟乙烯(PTFE)。O形圈与密封面触处的摩擦系数为0.25，丁腈橡胶的热膨胀系数设为175×10-6℃-1，聚四氟乙烯的热膨胀系数设为11.4×10-5℃-1。

橡胶属于超弹性材料，本研究分析中采用的橡胶模型是Mooney-Rivlin模型，应变能函数为：

W=C10(I1-3)+C01(I2-3)

(1)

式中，W—— 应变能密度

C10,C01—— 材料Mooney常数

I1,I2—— 第一、第二应变张量不变量

2 液压缸活塞密封结构数学模型

2.1 最大启动压力模型

EHA工作过程中，液压缸的启动压力主要源自密封件和配合面之间相对运动产生的摩擦力。该启动压力既给液压缸带来好处也产生危害。好处在于启动压力的存在形成液相薄膜，出现流体润滑现象；且在带有负载的情况下EHA运行更加平稳。危害是启动压力使密封件磨损破坏而缩短其使用寿命，并且摩擦生热使油液黏度降低从而导致泄漏量增大。

设摩擦系数为f，滑动润滑密封面上剪切应力为τ，由活塞格莱圈密封结构所引起的启动摩擦力F可表示为：

(2)

式中，D—— 液压缸缸体内径

L—— 密封接触面宽度

活塞壁面剪切应力为[15]：

(3)

式中， dp/dx—— 液相薄膜间的压力梯度

h—— 密封面间液膜厚度

把式(3)代入式(2)可得：

(4)

设最大启动压力为pm，则pm为：

(5)

式中，A—— 液压缸加载腔活塞有效作用面积

从式(5)可以看出，活塞密封结构的启动压力大小与密封接触面宽度、加载腔活塞有效作用面积、缸体内径、活塞运动速度和液相薄膜压力分布有关，而密封面间的液相薄膜压力分布梯度与液压缸活塞密封结构参数密切相关。

由于液压油液黏度μ值的大小随油液压力和温度的变化而变化，根据文献[16]，温度对μ的影响较大，且随着温度的升高，μ值减小。当忽略压力对油液的黏度μ的影响时，可得：

μ=μ0e-α(T-T0)

(6)

式中,μ0—— 油液在1个大气压、T0温度下的动力黏度，Pa·s，T0取20 ℃

α—— 油液黏温系数

T—— 油液温度，℃

将式(6)代入式(5)可得：

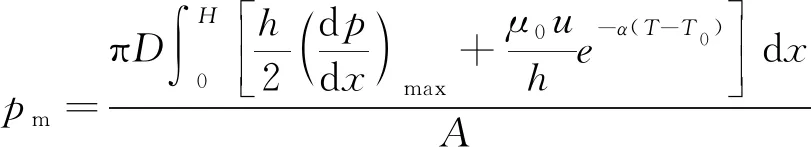
(7)

2.2 往复密封泄漏流量模型

液压缸活塞密封结构相对缸筒做往复运动，在密封面之间形成了一层薄薄的液相薄油膜。这层液相薄膜的形态直接影响液压缸活塞密封结构的密封性能。在恒定流情况下，设活塞沿x轴方向相对缸筒以速度u运动，密封面间液膜厚度可以采用一维稳态条件下的雷诺方程来求解：

(8)

式中，p—— 液膜压力(密封面间接触压力)

h—— 液膜厚度

ho—— ∂p/∂x=0时的液膜厚度

μ—— 油液黏度

u—— 活塞运动速度

从式(8)可以看出，密封面间流体形成动力润滑的条件是液膜必须呈收敛的楔形，即液膜厚度h沿x方向呈收敛的楔形变化。当h为常数，则右边为0，无法建立流体动压力。此外，密封面间必须存在相对运动，且油液必须有一定的黏度。

(9)

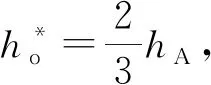
(10)

(11)

此时的内泄漏量为活塞伸出时黏附在活塞上的油流量。假设活塞直径为D，外行程时液压缸活塞密封结构的内泄漏量计算如下：

(12)

式中，D—— 活塞直径

L—— 活塞杆行程

uo—— 活塞杆伸出时的速度

(13)

在dp/dx=0处，也就是最大压力点处， 液相薄膜的流动速度分布从ui线性减小到0。在界面外的油压侧，液相薄膜具有匀速ui。 因此，其液相薄膜的高度hi为hi*的1/2，计算公式如下：

(14)

此时的内泄漏量为活塞缩回时黏附在活塞上的油流量。内行程时内泄漏量计算如下：

(15)

因此液压缸往复运动一次时的净内泄漏量为：

(16)

将式(6)代入式(16)可得:

Q=Qo-Qi

(17)

式(15)表明，密封面间液相薄膜压力分布与液压缸活塞密封单行程内泄漏量之间为反比关系。在活塞直径、活塞行程和速度已知的条件下，只要能够得到dp/dx大小，即可得到液压缸活塞密封结构的内泄漏量大小，本研究借助ABAQUS软件求取接触压力p的曲线，从而得到dp/dx的最大值。

3 计算结果分析

有限元几何模型的参数如表1所示，外形程和内行程速度均为1 m/s，环境温度变化范围为 (-20～100 ℃)，环境温度为20 ℃ 时油液黏度μ=0.07048 Pa·s，行程长度为30 mm，分别在介质压力为1， 7， 16 MPa时分析EHA活塞密封性能。

3.1 格莱圈内部Von Mises应力和接触压力

不同介质压力和环境参数下，对密封圈的性能要求不同。在密封圈材料和安装参数不变的情况下，当活塞行程为30 mm，活塞的运动速度为1 m/s时分别分析低(1 MPa)、 中(7 MPa)和高(16 MPa)介质压力下，格莱圈内部Von Mises应力和接触压力在宽温域(-20～80 ℃)内随温度的变化规律。

如图2～图4所示，为低、中和高压时，不同温度下格莱圈内部Von Mises应力τv分布云图，图5为不同介质压力下最大Von Mises应力随温度变化的曲线。从图2可以看出，低介质压力下，温度为-20 ℃时，最大Von Mises应力主要集中在方形圈内部，O形圈中心区域的Von Mises 应力较大；可明显看出低温下橡胶密封圈的可压缩性变差；随着温度的升高，O形圈的变形量增大，O形圈和方形圈内部区域最大Von Mises 应力也逐渐增大，方形圈内部Von Mises应力集中更明显，分布更均匀。从图3和图4可以看出，在中高介质压力下，随着温度的升高，格莱圈内部的Von Mises应力逐渐增大，最大Von Mises应力位于方形圈，在靠近介质一侧和密封间隙处出现Von Mises应力集中。从图5可以看出，不论低、中和高介质压力下，随着温度的升高，密封圈最大Von Mises应力增大；低压下，Von Mises应力随温度升高而增大的更为明显。

图2 介质压力1 MPa时，不同温度下格莱圈内部Von Mises应力云图

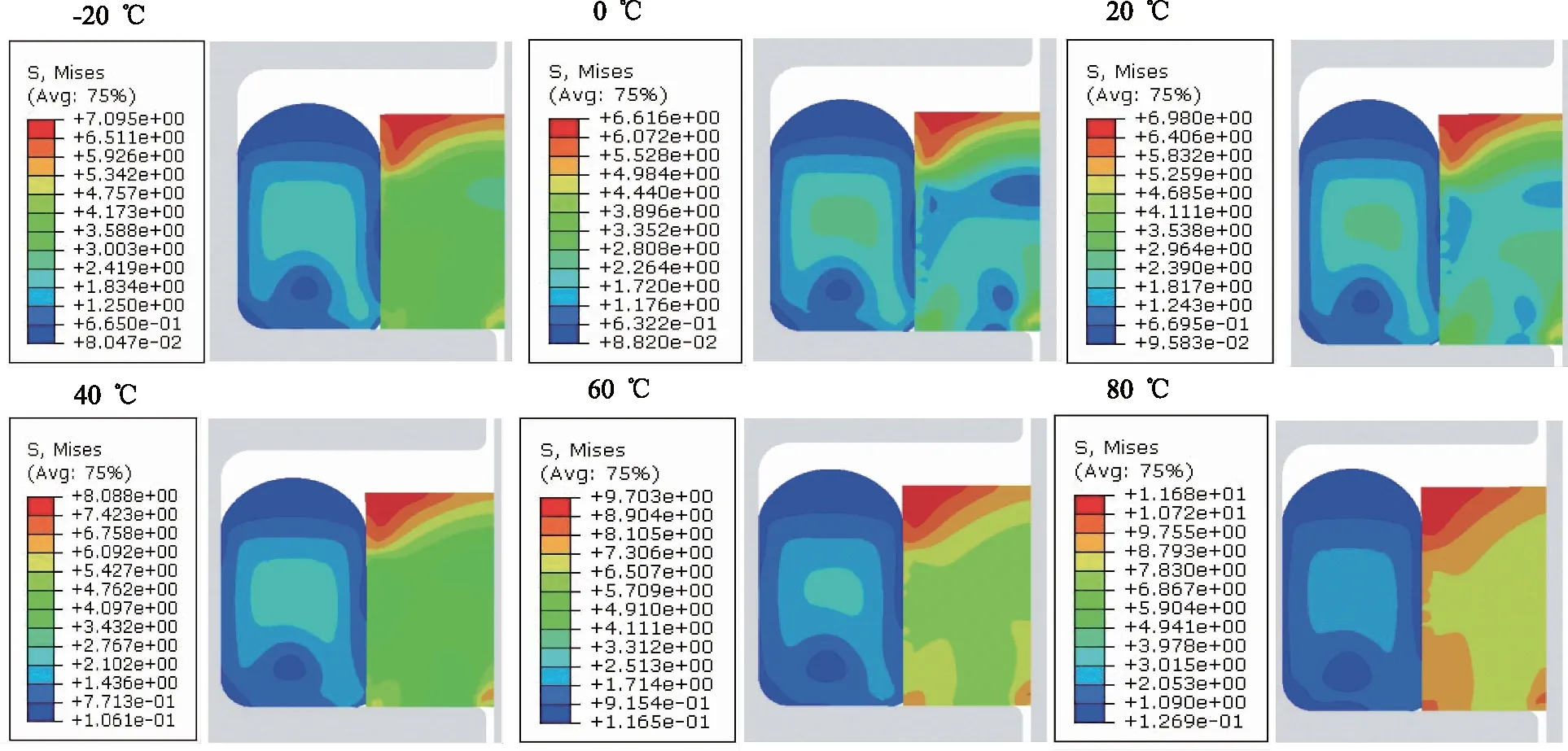
图3 介质压力7 MPa时，不同温度下格莱圈内部Von Mises应力云图

图4 介质压力16 MPa时，不同温度下格莱圈内部Von Mises应力云图

图5 不同介质压力下格莱圈内部最大Von Mises应力

综上分析，低压下，O形圈出现了Von Mises 应力集中；中高压力下，最大Von Mises应力集中于方形圈。总的来说，温度的升高增加了格莱圈失效的风险。

如图6所示为不同介质压力下，液压缸活塞格莱圈密封的密封面间接触压力随温度的变化曲线，表2为不同介质压力和温度下最大接触压力值。从图6和表2可以看出，低介质压力下，随着密封圈温度的升高，接触压力明显增大，温度为-20 ℃时的最大接触压力大于1 MPa， 温度为80 ℃时的最大接触压力约为-20 ℃时的3倍左右，几种不同温度工况下格莱圈可以起到密封作用。介质压力为7 MPa，温度从-20 ℃逐渐增大时，密封面间的接触压力也逐渐增大，但不及低介质压力下增加幅值大，温度为80 ℃时的最大接触压力约为-20 ℃的1.3倍左右，几种不同温度工况下的最大接触压力均大于7 MPa，格莱圈可以起到密封作用。高介质压力16 MPa下，温度为-20 ℃时，密封面间的最大接触压力小于介质压力，此时格莱圈密封失效；在温度逐渐升高时，密封面间的接触压力也逐渐增大，0 ℃时最大接触压力大于介质压力，即温度大于0 ℃时格莱圈可以起到密封作用。通过以上分析可以看出，随着介质压力的升高，密封圈密封有效的温度范围变小，即低中介质压力下，液压缸活塞密封有效的温域更宽；高介质压力下，0 ℃以下的低温域工况对液压缸活塞橡胶密封的要求更高。

图6 不同介质压力和温度下密封面间最大接触压力

表2 不同介质压力和温度下最大接触压力

3.2 最大启动压力和泄漏流量变化规律分析

基于3.1节中利用ABAQUS软件求出的接触压力曲线，即可求得(dp/dx)max的变化规律如表3所示。

使用HLM46号抗磨液压油，油液温度为20 ℃时，μo=0.07048 Pa·s，黏温系数α取1/23，方形圈与液压缸筒内壁的摩擦系数取0.03。根据表1所示几何结构参数和表3所示(dp/dx)max值，从而得到介质压力1, 7, 16 MPa时，单行程泄漏流量大小变化规律如表4和图7所示，最大启动压力变化规律如表5和图8所示。

表3 不同介质压力和温度下最大接触压力梯度(dp/dx)max

从表4和图7可以看出，由于橡胶材料的热胀冷缩现象，不论低中高介质压力下，单个行程的泄漏流量均随温度的升高而减小；相同温度下，随着介质压力的升高，泄漏流量逐渐减小。从表5和图8可以看出，同一介质压力下，随着温度的升高，液压缸活塞最大启动压力pm逐渐减小；相同温度下，随着介质压力的升高，pm逐渐增大。当介质压力相同时，温度每增加20 ℃，泄漏流量减小量不低于25%，最大启动压力减小量不低于15%。

图8 不同介质压力下，启动压力随温度变化曲线

表5 不同介质压力和温度下最大启动压力

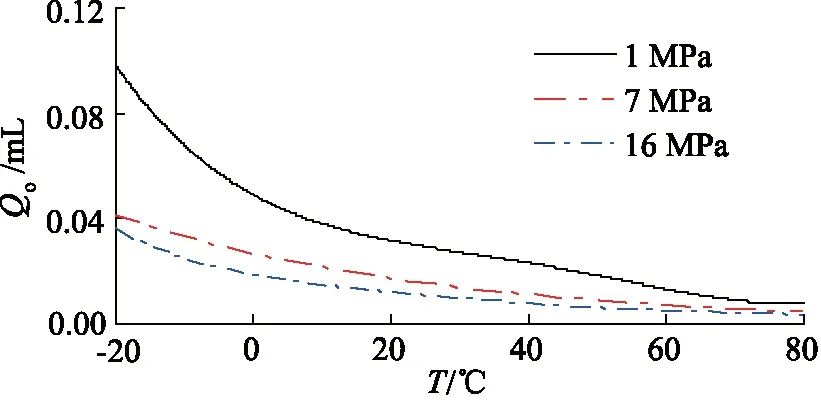
图7 不同介质压力下，单行程泄漏流量随温度变化曲线

表4 不同介质压力和温度下单行程泄漏流量

综上分析可知，当液压缸密封结构的参数不变，相同温度工况下，密封结构的泄漏流量与活塞最大启动压力大小呈负相关，符合实际应用；相同介质压力工况下，密封结构的泄漏流量与活塞最大启动压力均呈现逐渐减小的变化趋势，这与丁腈橡胶材料的热胀冷缩和易变形的特性有关。值得注意的是，液压缸活塞往复运行过程中，温度的适当升高有利于提高活塞密封结构的密封性能，但当温度超过80 ℃时，O形圈发生永久变形和老化的风险会大大增加，并且高温下橡胶密封圈变得更软，在液压缸活塞往复动密封中容易发生沿周向的扭转现象，这都将大大缩短液压缸活塞密封的使用寿命，从而增加了液压缸使用的故障率。

4 结论

(1) 不论低、中和高介质压力下，温度适当升高有利于降低最大启动压力和泄漏流量，然而增加了格莱圈失效的风险；

(2) 随着介质压力的升高，密封圈密封有效的温度范围变小，即低中介质压力下，活塞密封有效的温域更宽；高介质压力下，0 ℃以下的低温域工况对EHA活塞橡胶密封件的品质要求更高；

(3) EHA活塞格莱圈密封结构的泄漏流量随温度升高而减小，随介质压力升高而增大；最大启动压力随温度升高而降低，随介质压力升高而增大。过高的温度将增加格莱圈中O形圈永久变形的风险和老化程度，且在液压缸活塞往复动密封中容易发生沿周向的扭转现象，将大大缩短液压缸活塞密封的使用寿命，增加了EHA使用的故障率。