电液振动台正弦振动自适应控制方法

李昭阳， 关广丰， 熊 伟， 王海涛

(大连海事大学 船舶与海洋工程学院， 辽宁 大连 116026)

引言

电液振动台在振动实验中发挥的作用越来越关键。正弦振动是振动实验的重要组成部分，通常有定频、扫频两种实验模式。由于在产品有效性检验中具备重要作用，其在汽车、船舶、航空航天等各个领域的应用日益普及[1-3]。

虽然电液振动实验台输出力矩大、响应速度快，但受液压系统频宽的限制，正弦振动实验中加速度输出信号跟踪精度较低。同时，系统中存在的死区、摩擦力等因素，导致加速度输出信号波形失真度较大，这极大降低了正弦振动的控制精度[4]。针对波形跟踪精度低的问题，VASILIS K等[5]基于LMS算法设计自适应逆控制器，进行了波形再现实验研究；PLETT G L[6]对LMS算法稳定性、收敛性以及权值方程更新等进行了研究；沈刚等[7]基于滤波-x LMS算法进行了单轴电液振动台随机波再现实验研究； 何尧[8]对通过幅相控制补偿相位滞后的问题进行了研究。上述研究均采用基于LMS算法的控制策略，能够有效提高参考信号的跟踪精度，但算法收敛速度较慢，算法迭代系数需人为选取, 导致系统控制精度主要取决于操作员的熟练程度。RLS算法利用输入信号自相关矩阵的逆代替LMS算法中的迭代系数，实现了迭代步长的自动选取，且将算法收敛速度提高了一个数量级[9]。通过RLS算法构建自适应逆控制器，有助于进一步提高波形跟踪精度。

针对正弦波形失真度问题，很多学者对谐波抑制控制策略进行了研究。赵勇[10]以LMS算法及其变形为基础，进行了自适应谐波抑制控制器设计。姚建均[11-12]将谐波辨识技术应用于谐波抑制中，基于广义卡尔曼滤波对加速度谐波进行动态跟踪，但要求系统非线性不能过大。现有研究多为单次谐波抑制，在收敛速度和精度上仍旧有提升空间。HAYKIN S[13]提出快速块LMS算法，其理论基础源自快速傅里叶变换算法，能够实现卷积和其他相关算法的快速运算。该算法相较于一般LMS算法，具备计算量少、收敛速度快等优点。

本研究提出自适应逆控制及谐波抑制复合控制策略，通过带遗忘因子的RLS算法构建自适应逆控制器，提高正弦波形的跟踪精度。基于快速块LMS算法构建双次自适应谐波抑制控制器，减小系统加速度输出信号波形失真度。

1 自适应逆控制及谐波抑制复合控制策略

针对正弦振动控制中存在的波形跟踪精度差、失真度大问题，本研究提出自适应逆控制及谐波抑制复合控制策略，其基本原理如图1所示。

图1 正弦振动自适应逆控制及谐波抑制复合控制原理图

在伺服控制回路中，采用三状态反馈控制器提高系统阻尼，采用三状态顺馈控制器拓展加速度系统频宽， 控制器设计过程可参见文献[14]。系统加速度输出信号作为自适应逆控制器和自适应谐波抑制控制器的输入，提高波形跟踪精度，抑制谐波，提高正弦振动控制精度。

2 自适应逆控制器设计

自适应逆控制器利用自适应算法在线辨识系统的模型及逆模型，并利用逆模型对输入信号进行滤波修正，以提高响应信号的跟踪精度，自适应逆控制器原理如图2所示。

图2 自适应逆控制基本原理图

(1)

yR=ωR(n-1)u(n)

(2)

eR(n)=dR(n)-yR(n)

(3)

ωR(n)=ωR(n-1)+KH(n)eR(n)

(4)

P(n)=λ-1P(n-1)-λ-1k(n)uH(n)P(n-1)

(5)

式中，u(n) —— 滤波器输入信号

dR(n) —— 滤波器期望信号

yR(n) —— 滤波器输出信号

eR(n) —— 误差信号

H —— 共轭转置符号

λ—— 遗忘因子，其取值范围一般在0.98～0.995之间

ωR(n) —— 权向量

K(n) —— 增益向量

P(0)=δ-1I， 当系统信噪比较高时， 可取δ=

1×10-6。

3 基于快速块LMS算法双次谐波抑制控制器设计

谐波抑制的基本原理是通过指定频率的参考信号对自适应陷波器的陷波频率进行调节，进而利用陷波器实现指定频率的谐波抑制。单次谐波抑制只需给定一路参考输入信号，而双次谐波抑制需要设定两路不同频率的参考输入信号，双次谐波抑制控制器原理图如图3所示。

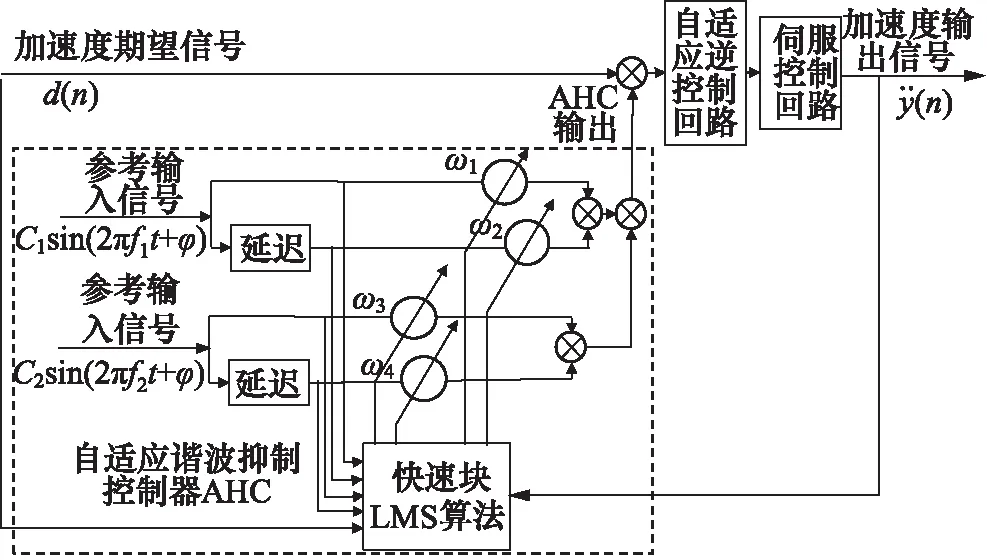
图3 自适应谐波抑制控制器原理图

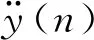
自适应谐波抑制控制器基于快速块LMS算法构建，快速块LMS算法计算公式为[13]

n=kN+i

(6)

(7)

(8)

ωL(k)=(1-μα)ωL(k+1)-f(uL(n),eL(n),μ)

(9)

(10)

式中,uL(n) —— 参考输入信号

yL(n) —— 滤波器输出信号

eL(n) —— 误差信号

ωL(n) —— 权向量

k—— 迭代次数

N—— 滤波器长度

α—— 权值遗忘因子

μ—— 步长

i—— 每个块中的迭代变量，0≤i≤N-1

快速块LMS算法原理图如图4所示。

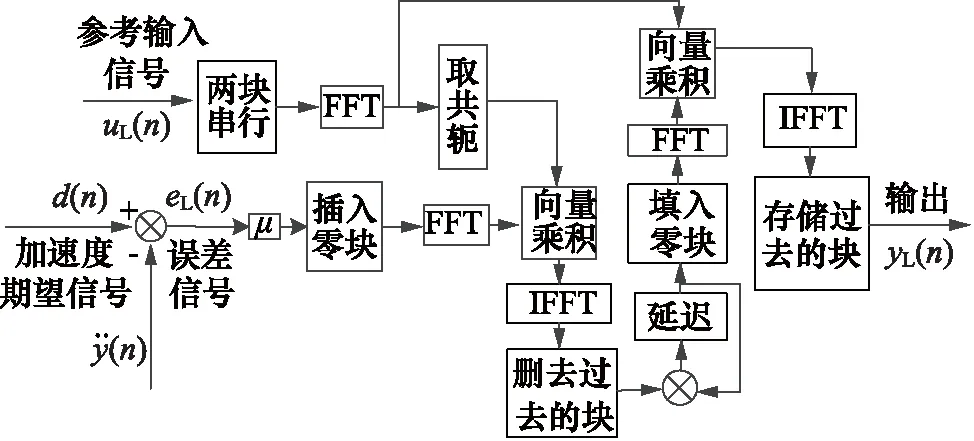
图4 快速块LMS算法原理图

图4中，FFT表示快速傅里叶变换；IFFT表示快速逆傅里叶变换。双次谐波抑制中, 快速块LMS算法有两路参考输入信号及其延迟总计4路输入信号。因此，实际运行过程中共有4路并行快速块LMS算法。

4 实验分析

利用图5所示六自由度电液振动台的5号缸进行正弦振动实验研究, 检验控制策略的有效性，图中编号1～6均为振动台的液压缸，振动台参数如表1所示。

表1 振动台参数

图5 电液振动台照片

4.1 波形失真度评价指标

依据液压振动台国标，以THD为加速度波形失真度评价标准[15]。取5次以内的谐波分量计算THD，计算公式为：

(11)

式中，A1—— 基波幅值

Ai—— 各次谐波幅值，i=2,3,4,5

4.2 实验结果分析

取正弦输入信号幅值为0.2g，频率为10 Hz，进行3组实验研究。第一组仅采用三状态控制策略，第二组采用三状态控制和自适应逆控制策略，第三组采用三状态控制、自适应逆控制及谐波抑制复合控制策略。

实验中，自适应逆控制器带遗忘因子的RLS算法的λ取为0.995，ωR(0)=0。谐波抑制控制器中快速块LMS算法的α取为0，μ取为1×10-4，滤波器长度取为32阶。

第一组实验中加速度a波形跟踪曲线和加速度输出信号幅值谱L(ω)如图6、图7所示。

由图6可知，输出正弦信号峰峰值为0.265g，10 Hz 处的幅频特性为-3.58 dB，存在波形滞后问题，波形跟踪精度较低。

图6 第一组实验加速度波形跟踪曲线

基于图7，根据式(11)计算可得第一组实验中的THD值为18.37%，波形失真比较严重。

图7 第一组实验加速度输出信号幅值谱

第二组实验中加速度波形跟踪曲线和加速度输出信号幅值谱如图8、图9所示。

由图8可知，输出正弦信号峰峰值为0.404g，10 Hz 处的幅频特性为0.09 dB，波形跟踪精度得到明显提高。

图8 第二组实验加速度波形跟踪曲线

由图9可计算第二组实验中的THD值为22.33%，虽然提高了跟踪精度, 但相比于第一组实验的波形失真度变大。

由图9可知, 4次和5次谐波幅值较大，第三组实验中针对4次和5次谐波进行抑制。谐波抑制控制器参考输入信号为sin(2π40t)、sin(2π50t)，同时抑制4次、5次谐波。加速度波形跟踪曲线和加速度输出信号幅值谱如图10、图11所示。

图9 第二组实验加速度输出信号幅值谱

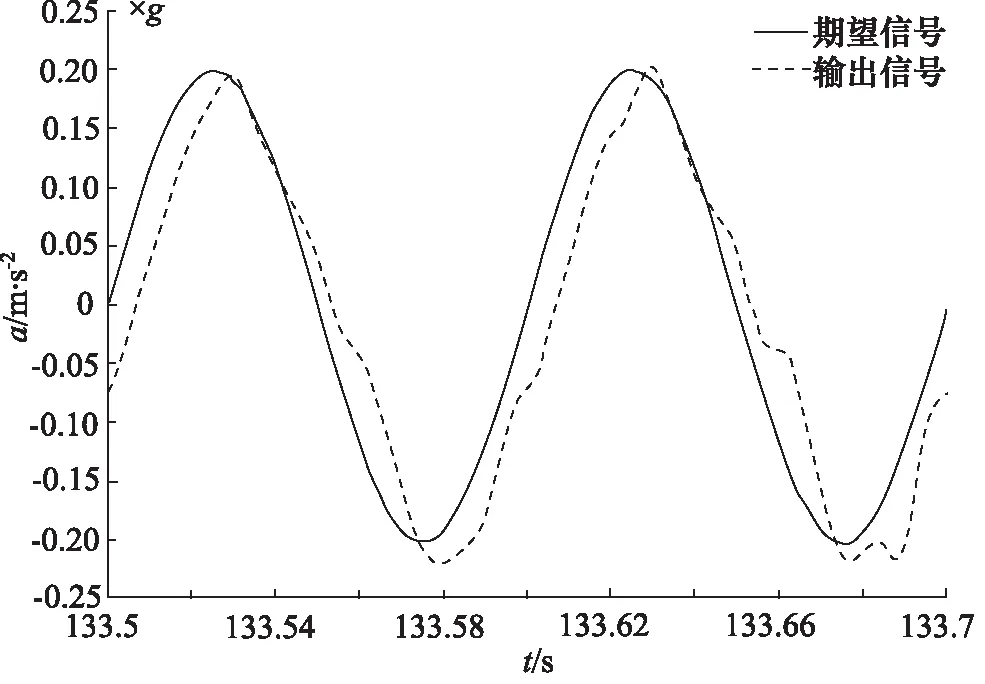
图10 第三组实验加速度波形跟踪曲线

由图10可知，输出正弦信号峰峰值为0.409g，10 Hz 处的幅频特性为0.20 dB，波形跟踪精度较高。

由图11可知，第三组实验加速度输出信号中4次和5次谐波基本完全消除，实现了双次谐波抑制。该组实验中加速度输出信号的THD值为11.79%，加速度输出信号波形失真度明显减小。

图11 第三组实验加速度输出信号幅值谱

5 结论

为了提高正弦振动的控制精度，提出了自适应逆控制及谐波抑制复合控制策略。基于带遗忘因子的RLS算法构建自适应逆控制器， 将10 Hz处的幅频特性由-3.58 dB提高至0.20 dB，明显提升了波形跟踪精度；基于快速块LMS算法构建双次自适应谐波抑制控制器，THD值由18.37%降低至11.79%，有效的抑制了双次谐波。实验研究表明，本研究提出的复合控制策略能够明显提高正弦振动实验的控制精度。