超压工况主蒸汽阀站先导阀的动态特性研究

刘 闯， 臧家林， 姚怀宇， 陈时健， 朱京梅， 金瑞兴， 钱锦远，5

(1.浙江大学 化工机械研究所， 浙江 杭州 310027； 2. 核电运行研究(上海)有限公司， 上海 200120；3.中核苏阀科技实业股份有限公司， 江苏 苏州 215129； 4.中国核电工程公司， 北京 100840； 5.浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州 310027)

引言

核电站的安全是核电站稳定运行的基础[1]。主蒸汽阀站作为核电站二回路中的三级超压保护设备之一，位于安全壳外，对主蒸汽系统的安全可靠运行起关键作用。主蒸汽阀站是由主蒸汽快速隔离阀、大气释放阀前置隔离阀(简称：前置隔离阀)以及监测主蒸汽安全阀和工作主蒸汽安全阀组成的阀组。主蒸汽阀站中的各个主阀均采用先导控制方式，利用系统自身介质压力来实现主阀自紧式密封。当系统压力超出安全范围时，即超压工况，阀内流体推动先导结构开启卸压，进而带动主阀开启，使系统压力恢复正常。随后，先导结构逐渐关闭使主阀恢复关闭状态[2]。因此，先导结构的动态特性直接决定整个阀门的响应性能。

对先导阀动态特性的研究焦点目前放在了结构参数上。陈雨洋等[3]利用AMESim软件对先导式水击卸压阀搭建了仿真模型，模拟了实际水击现象，分析得到节流阀直径、阻尼孔直径、主阀阀芯锥角对阀门的压力超调量、启闭时间有较大影响。任恒等[4]通过正交试验与仿真分析的方法，得出影响先导式比例减压阀动态综合特性的3个因素的顺序为主阀芯阻尼孔直径、先导流量稳定器阻尼孔直径和弹簧刚度。于德勇等[5]采用动网格技术对某核电厂的大气释放阀前置隔离阀开启特性进行研究，得出先导式阀门开启总时间主要是由卸压排放时间决定的。

由于先导阀是通过进口压力提供的推力进行运动，因此进口边界条件对先导阀动态特性的影响较大，但当前对于进口边界条件的关注较少。SONG等[6]利用动网格方法模拟了与压力容器连接的直动式安全卸压阀的启闭过程，发现减小压力容器进口容积会使响应时间延迟，振荡加剧。QIAN等[7]利用CFD方法对先导控制截止阀的流动和空化特性进行了数值模拟，研究表明，气体体积分数在靠近出口管的阀座处达到峰值，入口速度越高或阀芯位移越小，气蚀损伤越大。李树勋等[8]通过对水击卸压阀在不同超压比下的数值模拟发现，随着阀前超压比例的增加，阀芯运动到额定位移的时间相应缩短，阀芯速度、泄放量及阀芯所受液动力变化幅度会相应增大。

由于试验成本较高，理论分析难度较大，目前阀门动态特性的研究主要采用数值模拟方法。陈志杰等[9]使用不同湍流模型计算了核级定压止回阀在不同调节范围下的压力损失，并与试验值进行对比，结果表明标准κ-ε和Realizableκ-ε模型计算结果与试验值偏差较小。叶志烜等[10]基于动网格技术对中线蝶阀启闭过程中的流场进行数值模拟，得到了不同开度下阀后流场涡旋的演化规律。陈俊翔等[11]针对先导式电液比例阀的主阀芯在运动过程中动静态特性存在较大差异的问题进行研究，并提出了一种非对称控制策略及变增益死区补偿算法。刘梦瑶等[12]利用Fluent和用户自定义特征(User Defined Feature，UDF)，模拟了某核电止回阀在高压工况下开启过程中的内部流动，分析总结了阀体和阀芯在不同开度下的应力分布及变形情况。

本研究利用CFD动网格技术模拟了主蒸汽阀站中的主蒸汽安全阀先导阀的瞬态开启过程，并研究了在不同的线性入口静压力增加速度，即超压速度下先导阀的响应时间、瞬态力等关键动态参数随时间的变化情况，为主蒸汽阀站中先导阀的性能提升和国产化提供了理论参考。

1 计算模型

1.1 几何模型

主蒸汽阀站的几何模型如图1所示，先导阀安装在工作主蒸汽安全阀上。为了模拟先导阀的开启过程，进口压力应达到先导阀的整定压力。在此工况下，主蒸汽快速隔离阀保持关闭，隔离上下游管道。而前置隔离阀和监测主蒸汽安全阀的整定压力小于工作主蒸汽安全阀，所以保持全开。先导阀是由NICO和VS66 2个先导阀相互连接组成的，结构如图2所示。NICO进口与主阀阀芯上腔相连通，而VS66与主阀阀体内腔相连通。

1.主蒸汽快速隔离阀 2.前置隔离阀 3.监测主蒸汽安全阀 4.工作主蒸汽安全阀

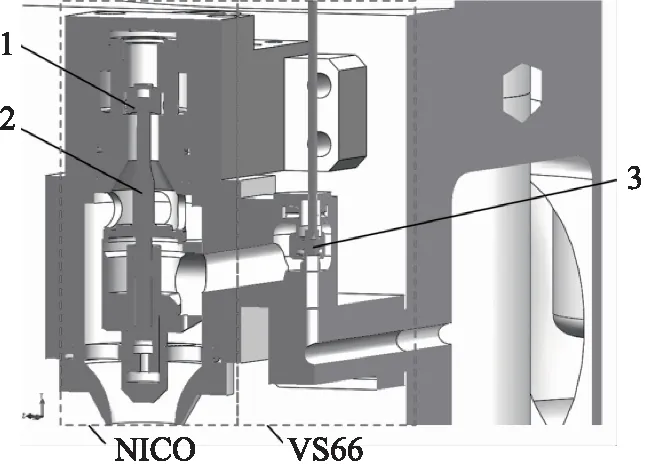
1.NICO套筒 2.NICO阀杆 3.VS66阀杆

先导阀控制主阀是通过进口超压流体推动VS66先导阀阀杆移动后，使NICO阀杆与VS66先导阀形成的腔内压力升高，进而推动NICO先导阀阀杆移动，使主阀上腔流体通过NICO先导阀卸压。主阀阀芯受力逐渐增加，主阀开启卸压。

1.2 网格模型

将几何模型封闭后抽取流道， 并使用WorkBench Mesh进行网格划分，如图3所示。

图3 主蒸汽阀站网格模型

对流道模型进行网格无关性验证，如表1所示。当网格数量达到1000万时能保证计算的精确性，并节省计算成本。具体采用5 mm的平均网格尺寸划分先导阀区域，采用20 mm全局平均网格尺寸，30 mm最大体网格尺寸划分主蒸汽阀站其余流道结构，并对局部区域进行网格加密，网格最小正交质量在0.1附近。对除阀体外的管道区域采用六面体网格进行划分，以提高计算速度和计算精度。对于整个主蒸汽阀站流道模型划分边界层以提高计算精度。

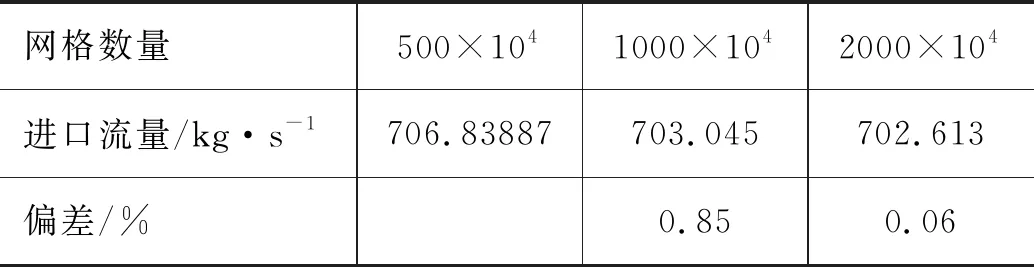
表1 不同数量的网格无关性验证

1.3 运动模型

整个瞬态开启过程中的运动部件有2个，分别为VS66阀杆和NICO阀杆。利用Fluent提供的动网格功能和UDF功能对阀杆的运动方式进行定义，并基于式(1)来编写不同的UDF文件：

dv=dt*(fy-fr-ky)/m

(1)

式中，fr—— 阀杆重力

ky—— 弹簧阻力，弹簧刚度k与阀杆在每一时刻的总上升高度y的乘积

dv—— 指阀杆在每个时间步的运动速度变化

dt—— 指时间步长

fy—— 流体推力

使用用户自定义函数读取所有流道与运动部件接触的网格内的压力值p与网格面表面积的乘积。

进口压力值作为本研究的变量，分别设置3种线性超压速度值进行模拟，如式(2)、式(3)所示。

ps=psi+x*t

(2)

pt=pti+x*t

(3)

式中，ps—— 进口静压力

psi—— 流场的初始压力，8.43 MPa

pt—— 进口总压力

pti—— 流场的初始总压力

x—— 超压速度，分别设置为1，2，3 MPa/s

t—— 流动总时间

1.4 分析模型

用Fluent软件建立分析模型。由于流动介质是过热蒸汽，将其看作理想可压缩气体，采用理想气体模型。选择基于密度的求解器，通过能量方程和Realizableκ-ε湍流模型进行求解，边界条件如表1所示。在UDF文件中，通过设置提高速度来实现进口静压力线性增长；同时，为了使进口动压不发生变化，需要将压力进口边界条件中的总压同样设置为随时间变化。为了保证瞬态计算结果，将稳态计算结果作为初始流场进行计算。

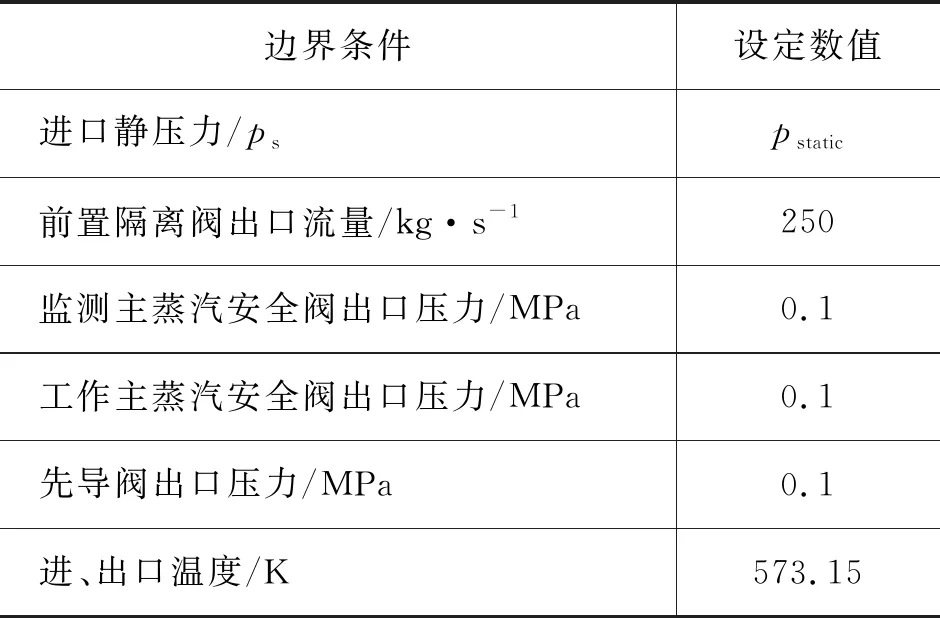
表2 主蒸汽阀站边界条件

2 计算结果与讨论

2.1 响应时间分析

VS66阀杆在不同进口超压速度下的运动曲线如图4所示，VS66的开启运动过程整体呈曲线上升状态，刚开启时的波动幅度较大，随着开启高度逐渐增加，波动幅度逐渐变小。当进口静压力随时间线性增长时，VS66阀杆的波动幅度和波动次数均大于进口压力恒定时。提高超压速度会减小VS66阀杆在开启过程中的波动幅度，以及缩短波动时间。

图4 不同超压速度下VS66阀杆运动曲线

此外，到达最大开度的响应时间在进口压力恒定时，均小于线性增长情况。提高超压速度能缩短VS66先导阀的总开启时间。超压速度由1 MPa/s提高到2 MPa/s 过程中，在开度到达一半之前的运动曲线几乎完全重合，随后才逐渐分离。当超压速度小于2 MPa/s 时，对于波动幅度、波动时间的影响很小，但会使阀杆开启高度达到1.25 mm后的开启速度略微增加，VS66的总开启时间略微缩短，缩短程度为41%。当超压速度由2 MPa/s 提升至3 MPa/s时，VS66的总响应时间显著缩短。

NICO阀杆运动过程如图5所示，与进口压力恒定时相比，开启过程运动趋势并没有太大变化，开启过程没有波动， 均为抛物线式上升。进口压力恒定时的总开启时间和最初开启时间均小于存在超压速度时。这意味着在实际工况中，若上游压力继续增大，可能会引起主蒸汽阀站超时响应。在超压速度由1 MPa/s提高到2 MPa/s时，NICO的开启曲线几乎没有变化，而在超压速度提升至3 MPa/s时，提高超压速度会略微缩短NICO的总开启时间，以及显著减小NICO的最初开启时间，使其由1 MPa/s时的0.008 s缩短至0.006 s，缩短了25%。NICO的最初开启时间与VS66的开启过程有关，由于超压速度为1 MPa/s和2 MPa/s时，VS66运动曲线几乎不变，因此，NICO运动曲线也几乎不变。

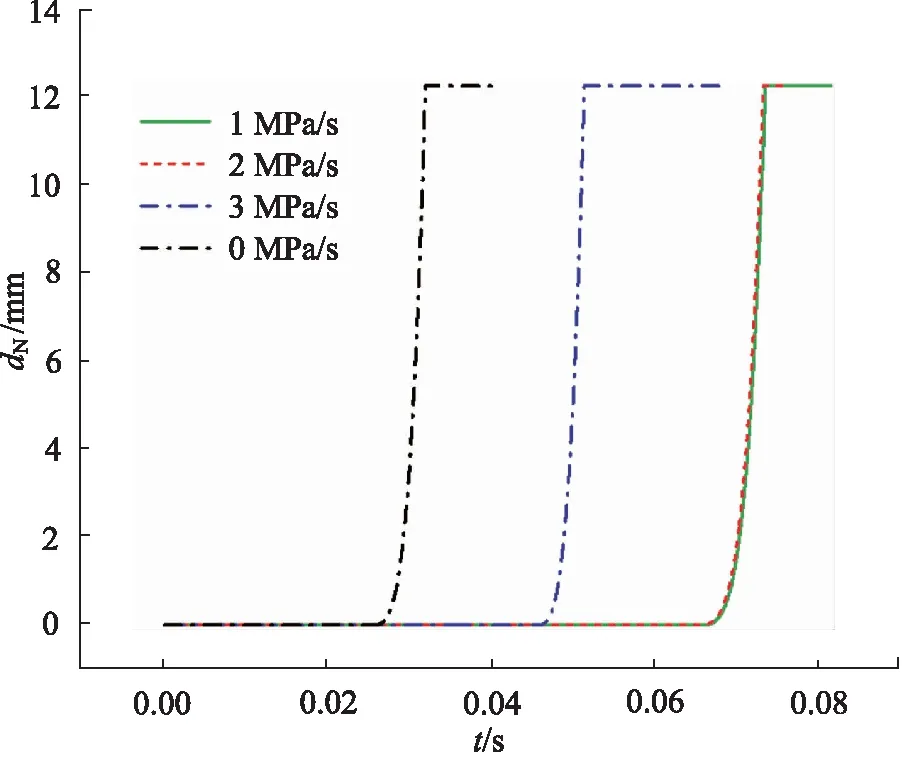
图5 不同超压速度下NICO阀杆运动曲线

进口压力线性增加时，会改变2个先导阀之间的开启延迟时间，且超压速度越大，开启延迟越小。可以看出，在超压速度逐渐增加时，NICO达到最大开度的时刻所对应的VS66开度逐渐增加，分别对应1.774，1.874， 2.000 mm。这是由于超压速度的增大导致VS66到达最大开度的时刻提前，从而导致NICO到达最大开度的时刻相对延后。

2.2 阀杆受力分析

VS66和NICO阀杆在运动过程中的最大受力值发生在阀杆到达最大开度的时刻，具体值如表3所示。可以看出，超压速度为3 MPa/s时，VS66和NICO阀杆的最大受力值超过其余3个工况。在超压速度为0，1，2 MPa/s时，VS66阀杆最大受力值类似。而超压速度为0 MPa/s时的NICO阀杆的最大受力值大于超压速度为1和2 MPa/s时。

表3 先导阀阀杆运动过程中的最大受力值

VS66阀杆在不同超压速度下的受力随时间的变化曲线如图6所示，阀杆所受推力的变化也代表着运动加速度的变化。有超压速度的受力曲线与未有超压速度时的阀杆受力曲线变化趋势大致相同。在受力刚开始增加达到2500 N附近时，阀杆受力突然下降，随后又快速增大。改变超压速度并不会改变此刻的波动幅度和波动时间，但会使该波动过程略微提前。随后阀杆受力增大到4700 N附近时，增大速度逐渐变缓。

图6 不同超压速度下VS66阀杆受力曲线

两者受力曲线的区别在于，进口压力线性变化时，受力大于4700 N后的平均增加速度均小于进口压力恒定时；且进口压力增加速度越快，受力的平均增加速度也越快，受力的波动时间越短，到达最大开度时刻的受力值也越大，这也是阀杆运动总时间逐渐缩短的原因。但超压速度由从1 MPa/s提高到2 MPa/s时，整体改变效果不大。

NICO阀杆在不同超压速度下的受力变化曲线如图7所示，有超压速度的受力曲线与未有超压速度时的阀杆受力曲线变化趋势大致相同， 均存在2个突变点，分别对应NICO先导阀开启时刻和到达最大开度时刻。

图7 不同超压速度下NICO阀杆受力曲线

两者受力曲线区别在于，所有超压速度下的受力变化曲线的变化速度均小于进口压力恒定时。在NICO先导阀最初开启时刻的受力值均大致相同，这是由NICO先导阀的整定压力决定的。当超压速度为0，1，2，3 MPa/s时，NICO先导阀到达最大开度时的受力值分别为24359，23674，23715，25036 N。因此，当超压速度由2 MPa/s提高到3 MPa/s时，NICO到达最大开度时的受力值大于进口压力恒定时。提高超压速度均会增大NICO阀杆的受力提高速度，这使得NICO阀杆最初开启时间和达到最大开度的时间略微提前。从曲线中可看出，超压速度从1 MPa/s提高到2 MPa/s时，整体改变效果不大，2条曲线几乎重合。超压速度由2 MPa/s 提高到3 MPa/s时，曲线整体变化较大，阀杆受力的提高速度更大，开启时间也略微提前。

2.3 先导阀响应延迟原因分析

存在超压速度时，2个先导阀的响应时间均大于进口压力恒定时。为分析超压速度的影响原因，在NICO阀杆受力为0 N的时刻，即运动时刻为0.02556 s 时，可视化2个先导阀对称面处的压力分布，如图8所示。

图8 先导阀压力分布对比(运动时刻为0.02556 s)

从图8中可以看出，同一时刻下，超压速度存在使VS66先导阀阀腔内的压力升高速度变慢，同时，从VS66先导阀内流向NICO先导阀阀杆下底面的流体减少，NICO下底面的压力升高速度减慢。

当超压速度为3 MPa/s时，NICO阀杆受力为0 N的时刻为0.0456 s，在该时刻不同超压速度影响下，压力分布的变化如图9所示。

图9 先导阀压力分布对比(运动时刻为0.0456 s)

可以看出，当NICO阀杆受力为0 N时，超压速度为3 MPa/s时的压力分布与未有超压速度时几乎相同，这是因为NICO的开启压力不变。当超压速度由3 MPa/s下降至2 MPa/s时，VS66阀杆外腔的压力升高速度减慢，导致NICO阀杆下底面的压力升高速度减慢，因此2个先导阀到达最大开度时间都同时延后。

3 结论

分析了主蒸汽阀站的先导阀开启过程中的动态特性，对不同超压速度下的响应时间和瞬态受力进行分析，得出如下结论：

(1) 超压速度提高时VS66和NICO先导阀的响应时间均会更短，表现能力更好，但均弱于进口压力恒定时的情况。进口压力线性变化，可能使主蒸汽阀站响应时间超过恒定进口压力时；

(2) 超压速度在3 MPa/s时，NICO和VS66阀杆的最大受力值均大于其余3个工况。在0，1，2 MPa/s时，VS66阀杆的最大受力值近似相等。而在0 MPa/s时，NICO阀杆的受力值大于1和2 MPa/s时的受力值；

(3) 超压速度会加剧VS66阀杆在开启过程中的波动幅值，延长波动时间，但对NICO的开启过程曲线走势以及NICO的总开启时间影响不大。本研究中的工况条件已经是主蒸汽阀站所使用的最极端工况，在实际运行中要避免其发生，因此在阀站其余阀门的泄放作用下，当超压速度过大(超过3 MPa/s)时，超压工况出现的概率较小。