比例电磁铁推拉储能式PWM功放电路

强 彦， 杨丹丹， 孙 辉， 赵保才， 邹洪波， 魏列江

(1.兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050；2.江苏汇智高端工程机械创新中心有限公司， 江苏 徐州 221004；3.杭州电子科技大学 自动化学院， 浙江 杭州 310018)

引言

为满足高性能电液比例控制系统中工业装备整机功率不断加大、控制系统精度与响应速度不断提高的应用需求，电液比例阀正朝着大流量、高频响、控制智能化的方向发展[1-3]，而大功率高频响比例电磁铁作为大流量高频响电液比例阀的电-机械转换器，其响应速度是影响比例阀动态特性的重要因素[4-5]。对于确定参数的比例电磁铁，其功放电路的性能决定了电磁铁线圈充、放电时间的长短，从而限制了比例电磁铁的响应速度[6-9]。现有比例电磁铁线圈均采用PWM开关式功放电路驱动，主要有单管调制式[10-11]和反接卸荷式[11-14]：单管调制式功放电路结构简单，功耗较低，但线圈充、放电速度均较慢；反接卸荷式功放电路在比例电磁铁线圈放电时将电源电压反接在线圈两端，针对额定电流为1A的比例电磁铁线圈，放电时间与单管调制式功放相比缩短了80%。1998年，德国力士乐[11]提出了高电压驱动法，通过提高母线电压来加快电流的上升速度。2010年，聂勇[11]在反接卸荷式功放电路的基础上提出一种三态调制式功放电路，通过改进PWM信号的调制方式在一定程度上提高了比例电磁铁的动态性能。2017年，徐兵等[13]建立了反接卸荷式功放电路的非线性数学模型，并提出新型电流控制器用以消除零位滞后现象。2020年，刘宁等[14]提出了一种双边驱动电路，应用其对应的控制逻辑，可避免断流现象。一些研究人员通过改善高速电磁阀线圈的续流方法及激励电压施加方式来加快其动态响应[15-17]。于正同等[18-19]在电磁阀的驱动电路中增加了接口保护电路，并采用分组电流控制方法，提高了电磁阀的响应速度。以上研究均针对小功率低电流电磁铁功放电路的不同方面进行了设计与改进，但对于大流量高频响阀，例如力士乐4WRLD系列、4WRPH6系列等阀的比例电磁铁线圈，其额定电流往往不小于2.5 A，且该类阀对线圈的充放电速度要求更高，而上述功放电路在该方面仍存在不足。

针对传统功放电路难以满足大电流高频响比例电磁铁线圈快速充放电要求的问题，本研究提出一种推拉储能式PWM功率放大电路。通过在比例电磁铁的功放电路中设置储能模块，使线圈需要快速放电时，利用储能模块将线圈存储的能量进行回收，缩短比例电磁铁线圈的放电时间；线圈需要快速充电时，储能模块释放能量，补充电源电流输出，缩短线圈的充电时间，由此加快了比例电磁铁的响应速度，且该驱动电路的输出电流动静态性能良好。

1 推拉储能式PWM功放理论分析

1.1 工作原理

图1为推拉储能式PWM功放原理图，推拉储能式功放包括储能模块与非对称桥臂模块，储能模块由升压储能单元及过压保护单元组成，其中升压储能单元主要包括储能电容与稳压二极管，该单元可根据所驱动比例电磁铁的不同，灵活改变电容与二极管之间的连接形式，如多电容串联提高耐压值以达到目的高压，多电容并联增大容值来存储更多能量等，从而实现最佳驱动。非对称桥臂模块由2个功率MOS管Q1，Q2和2个续流二极管D4，D5组成。非对称桥臂中间连接比例电磁铁，两桥臂上的功率管与二极管交替导通与截止，实现比例电磁铁线圈的充电与放电，该功放电路存在开关函数F：

图1 推拉储能式PWM功放原理图

(1)

当F=1时，形成比例电磁铁线圈的充电回路，储能模块释放能量；当F=0时，形成电磁铁线圈的放电回路，储能模块吸收能量。

1.2 工作过程

以图2储能形式为例，对推拉储能式PWM功放的具体工作过程进行说明，电路做如下简化：

(1) 忽略比例电磁铁的非线性电感，将其等效为电感-电阻串联的L-R模型[20-22]，L为比例电磁铁等效电感，R为比例电磁铁等效电阻；

(2) 功率管及二极管的导通电阻相对于负载非常小，故认为各状态下这些电阻相等，均为RS。

设ion(t)为比例电磁铁线圈充电状态下的电流，ioff(t)为比例电磁铁线圈放电状态下的电流，τ=L/R为比例电磁铁时间常数，VCC_1为电源电压，T为PWM信号的周期，D为PWM信号的占空比，0≤D≤1。

1) 状态1，t∈[0,DT]

状态1为比例电磁铁线圈初始充电过程。控制信号PWM_HO与PWM_LO均为高电平，Q1，Q2导通，D4，D5截止，此时形成2条充电回路，如图2a所示，回路1：电源电压VCC_1经D1，D2向储能电容C1充电；回路2：电源电压VCC_1经二极管D1，D2对比例电磁铁线圈充电，线圈电流逐渐上升到稳态值。根据基尔霍夫电压定律，可得：

(2)

解得：

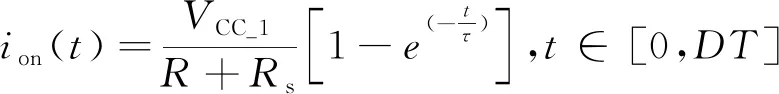
(3)

2) 状态2，t∈[(k+D)T,(k+1)T]，k=0,1,2，…，n

状态2为比例电磁铁线圈的放电过程，即推拉储能的“拉”状态。控制信号PWM_HO与PWM_LO均为低电平，Q1，Q2截止，D4，D5在线圈等效电感的续流效应下导通，形成如图2b所示的放电回路，线圈存储的能量经该回路进入储能电容中，电压迅速增高。推拉储能式功放电路在线圈放电状态下等效回路为二阶电路，根据基尔霍夫电压定律可得：

(4)

解得：

ioff(t)=ioff(0)e-αtcos(ωdt)+

t∈[(k+D)T,(k+1)T],k=0,1,2，…，n

(5)

uC1—— 储能电容上的电压

3) 状态3，t∈[kT，(k+D)T],k=1,2,3，…，n

状态3为比例电磁铁线圈的非初始充电过程，即推拉储能结构的“推”状态。PWM_HO与PWM_LO均为高电平，Q1，Q2开启，D4，D5截止，该状态也形成2条充电回路，如图2c所示，回路1：电源电压VCC_1经D1，D2对比例电磁铁线圈充电； 回路2： 储能电容C1

图2 推拉储能式功放工作过程

上的电压加载到比例电磁铁线圈上。当电压下降到与电源电压相等时，回路1开始工作，在回路1与回路2的共同作用下，线圈电流迅速“推”升到稳态值。推拉储能式功放电路在状态3中分为2个阶段：

(1) 阶段1，uc1>VCC_1该阶段储能电容向比例电磁铁供电，根据基尔霍夫电压定律(KVL)可得到：

(6)

解得：

ion(t)=iL(kT)e-αtcos(ωdt)+

t∈[kT,(k+D)T],k∈N，且uC1>VCC_1

(7)

式中，iL—— 比例电磁铁等效电感上的电流。

(2) 阶段2，uc1≤VCC_1该阶段由电源电压VCC_1向比例电磁铁充电，因此可得到：

(8)

解得：

t∈[kT,(k+D)T],k=1,2,3,…,n,且uC1≤VCC_1

(9)

通过以上分析可以看出，比例电磁铁推拉储能式PWM功放电路进行工作时，先经过状态1，再在状态2和状态3之间互相转换，利用线圈存储的能量并借助储能电容实现了比例电磁铁线圈电流快速跟随给定信号，进而完成功率放大的作用。

1.3 功放电路阶跃响应对比

推拉储能式与反接卸荷式两种功放电路的PWM信号与线圈电流的对应关系，如图3所示，PWM信号为高电平时，比例电磁铁线圈充电，PWM信号为低电平时，比例电磁铁线圈放电。在比例电磁铁线圈充电时，两种功放对PWM上升阶跃信号的响应表述为：

图3 PWM信号产生的比例电磁铁线圈电流

(10)

对PWM下降阶跃信号的响应表述为：

(11)

进而得到比例电磁铁线圈的充电与放电速度如式(12)、式(13)所示。在时间t一定时，线圈的充放电速度取决于加载到比例电磁铁两端的电压，电压越高，充放电速度越快。而推拉储能式PWM功放电路中储能模块的存在，使得线圈能量存储到储能电容C1时，电压uC1升高，当uC1>VCC_1时，推拉储能式线圈充电速度快于反接卸荷式，推拉储能式线圈放电速度快于反接卸荷式。在推拉储能式功放中，比例电磁铁线圈的充放电速度均优于传统功放，因此阶跃响应更迅速。

(12)

(13)

2 仿真研究

为验证推拉储能原理的有效性，本研究在Multisim软件中搭建了推拉储能式PWM功放电路的仿真模型，并对其仿真结果进行了分析，仿真参数如表1所示。

表1 功放电路主要参数

对推拉储能式PWM功放电路做0～3.2 A的上升阶跃和3.2～0 A的下降阶跃仿真，并与单管调制式和反接卸荷式两种功放电路进行比较，仿真结果如图4与图5所示，上升阶跃响应中，反接卸荷式功放电路的上升时间约为38 ms，推拉储能式功放电路的上升时间则为28.4 ms，推拉储能式功放的电流上升速度得到了显著提升，上升到线圈稳态电流所需时间更短，推拉储能式PWM功放相较于反接卸荷式功放电流阶跃响应时间缩短了近25%；在下降阶跃响应中，与反接卸荷式功放电路相比，推拉储能式功放电路的电流衰减时间也明显缩短， 反接卸荷式功放的电流衰减时间约为3.5 ms，而推拉储能式功放仅为1.9 ms，电流衰减时间相比反接卸荷式缩短了46%左右。由此可见，推拉储能式功放电路明显缩短了线圈的充放电时间，加快了比例电磁铁的响应。

图4 上升阶跃响应仿真波形

图5 下降阶跃响应仿真波形

3 实验验证

3.1 功放电路实验装置

依据本研究提出的推拉储能原理，设计了推拉储能式PWM功放电路的原型样机，并进行实验研究。实验装置如图6所示，其中直流稳压电源提供+24 V直流电压，示波器采集并记录比例电磁铁电流波形及数据，功率驱动板所需PWM控制信号由开发板给出，比例电磁铁型号为GP63S。

1.PC机 2.示波器 3.直流稳压电源 4.开发板 5.推拉储能式功放原型样机 6.比例电磁铁

对比实验包括比例电磁铁线圈的上升阶跃与下降阶跃响应实验，并将实验结果与仿真结果进行比较。

3.2 实验结果分析

图7和图8分别为推拉储能式与反接卸荷式功放电路0～3.2 A的上升阶跃与3.2～0 A下降阶跃响应实验波形。其中，PWM信号峰值为3.3 V，频率为5 kHz，通过测量采样电阻R0两端电压间接获取比例电磁铁的输出电流。从上升与下降阶跃的实验波形可以看出，反接卸荷式功放电路的上升阶跃时间(上升到稳态电流的90%)约为39.4 ms，而推拉储能式功放电路上升到稳态电流的速度加快，上升时间为29.9 ms，相比之下电流上升时间缩短24%。从图8可以看出。反接卸荷式功放电路的下降时间为4 ms，推拉储能式功放电路的下降时间为2.2 ms，相比反接卸荷式功放，推拉储能式功放电路的下降阶跃响应时间缩短了45%。将仿真结果与实验结果汇总并进行比较，结果见表2，可以看出两种功放电路的阶跃响应时间仿真与实验结果基本吻合。

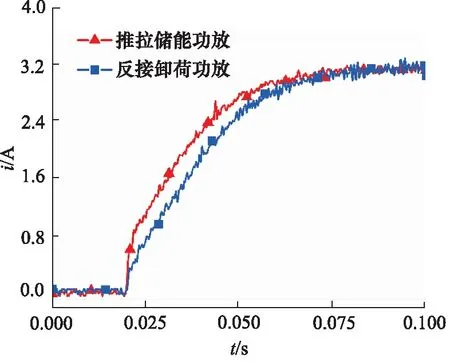
图7 上升阶跃响应实验波形

图8 下降阶跃响应实验波形

表2 阶跃响应仿真及实验结果

4 结论

本研究提出并实现了一种基于推拉储能原理的比例电磁铁PWM功放电路，通过对电路模型的仿真与原型样机的实验对该功放电路进行了分析验证，仿真与实验结果表明推拉储能式功放电路具有以下特点：

(1) 在比例电磁铁功放电路中设置储能模块，储能模块在电磁铁线圈放电时吸收线圈存储的能量，并在线圈放电时将其释放，利用该能量转化成的高电压加快了比例电磁铁线圈的充放电速度，缩短了线圈充放电时间；

(2) 上升阶跃响应中，推拉储能式功放电路的比例电磁铁线圈充电时间相比传统反接卸荷式功放电路缩短了24%，下降阶跃响应中，线圈放电时间相比反接卸荷式缩短了45%，推拉储能式功放电路显著提高了比例电磁铁的响应速度；

(3) 将比例电磁铁线圈能量通过储能模块进行回收，并再次用于比例电磁铁驱动，实现了能量的二次利用可对比例电磁铁的功放电路设计提供一定的参考。