谐波齿轮传动系统柔轮应力的数值建模与分析

2022-10-14穆塔里夫阿赫迈德张伟国孙光耀陶兴伟

机床与液压 2022年1期

穆塔里夫·阿赫迈德，张伟国，孙光耀，陶兴伟

(1.新疆大学机械工程学院，新疆乌鲁木齐 830047；2.新疆大学电气工程学院，新疆乌鲁木齐 830047)

0 前言

谐波齿轮传动是一种依靠弹性变形运动来实现齿轮间啮合的新型机构，主要由柔轮、刚轮和波发生器三部分组成，具有结构简单、零件少、体积小、质量轻、同时啮合齿数多、传动平稳、转动惯量小、侧隙小、精度高、承载力高、噪声低和同轴性好的特点，广泛应用于航空航天、汽车、精密光学设备和医疗器械等工业领域[1-2]。在运转过程中，椭圆形的波发生器使柔轮发生较大变形且与刚轮接触，而柔轮和刚轮的每个轮齿都要进行啮合[3]。由于谐波齿轮传动具有循环周期性，在啮合过程中，柔轮的齿根部位会随着周期性的啮合而容易发生疲劳破坏。因此，研究齿根的疲劳强度很有必要。为研究柔轮齿根的疲劳强度，需要对其齿根的应力进行实验测量。测量过程中，由于谐波齿轮结构的复杂性，测量的精度很难保证[4]。许多学者也对此进行了研究。牟如强[5]对谐波齿轮圆柱形齿轮进行应力分析，发现柔轮的变形量和最大应力越小、过盈量越小，谐波齿轮的使用寿命越长。陈茜等人[6]研究了在制造谐波齿轮时，各种误差对柔轮齿面应力的影响问题，提出了不同的补偿方案。陈晓霞等[7]研究了渐开线谐波齿轮的装配应力。蒋倩倩等[8]研究谐波齿轮传动齿廓对柔轮应力的影响。邱建喜等[9]对谐波减速器柔轮存在的疲劳问题进行了分析，并对其性能进行优化，提高了柔轮的使用寿命。

本文作者以柔性轴承波发生器杯型柔轮谐波齿轮传动系统为对象，对波发生器滚球、外圈和柔轮内圈的油膜进行模型简化并对其进行三维数值建模；对柔轮和刚轮在不同啮合深度时添加接触单元，用商用分析软件FAST进行应力分析，并与实验测试数据进行对比。计算结果与实验值在定性和定量方面吻合性较好。

1 谐波齿轮系统数值建模

1.1 谐波齿轮系统的结构

杯型谐波齿轮传动系统剖面图如图1所示，在系统的中间，柔性轴承波发生器是椭圆形状，其外圈与柔轮接触，接触面有一层较薄的油膜。在波发生器的长轴处，柔轮与波发生器的轴承外圈紧密接触；在短轴处，发生器与柔轮不接触且有许多滚球环绕。在系统中，波发生器存在3种主要的接触：通过轴承的滚球与轴承的内圈接触、滚球的外圈通过油膜与柔轮接触、柔轮与刚轮接触。本文作者主要对柔轮与刚轮接触进行建模和数值计算。

图1 谐波齿轮传动系统的剖面图

1.2 滚球的计算模型

谐波齿轮的转矩是通过波发生器轴承的滚球与柔性齿轮的内外圈接触传递的，可以将此传递转矩的模型简化成弹簧进行建模计算。弹簧的弹性系数可以通过赫兹弹性接触理论进行估值计算，弹性系数的值与接触载荷有关。邱建喜等[9]通过多次实验证明滚球的接触载荷幅值变化不明显，故可取其均值以确定弹性模量，弹簧模型的位移表达式为

F=-k(d-Δ)

(1)

式中：F为弹簧的力；k为弹簧常数；d为弹簧的位移；Δ为轴承的径向间隙。

1.3 油膜的计算模型

在对油膜进行数值建模时，采用16节点的等参数单元法，这是因为柔轮与刚轮只有在接触时该单元才从模型插入，分离时该单元将移除。采用此节点法,参数单元、节点总数和节点顺序不会因为油膜层单元的接触而发生改变。该单元只在油膜的法向传递法向力，不传递剪切力。故可采用空间极坐标系，对材料常数进行确定[10],如式(2)所示：

(2)

式中：Err为径向弹性模量；Eθθ为周向弹性模量；Grθ为剪切弹性模量。

1.4 刚轮与柔轮的接触单元

在刚轮和柔轮相互啮合时插入接触单元，并计算啮合过程中齿轮所受的总法向力，用它来评估齿轮在啮合过程中的柔轮应力情况。若计算的总法向力为负值，则表示柔轮与刚轮相啮合；若为正值，则表示不接触，即研究的某对柔轮与刚轮没有啮合。假设该单元的弹性模量E=206 GPa。柔轮的转动会使柔轮与刚轮在啮合时的接触区域发生改变。图2所示为柔轮与刚轮在不同啮合深度时对接触单元的影响。由于刚轮尺寸较厚，可认为刚轮为刚体，故认为刚轮的接触变形可忽略不计。即刚轮的变形位移可设为0,则可简化模型以方便计算。

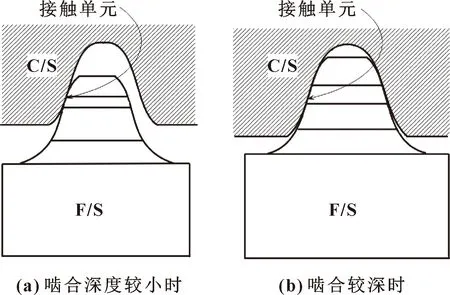
图2 插入接触单元时柔轮与刚轮不同啮合深度时的情况

1.5 谐波齿轮系统有限元模型

简化后的杯型谐波齿轮传动系统三维模型如图3所示。当输入不同的转矩时，轴承的滚球接触个数不同。当输入转矩为0时，接触滚动球的个数为9；当转矩为329 N·m时，共有13个球与之接触。故可以将滚球简化成一条线，将椭圆形的波发生器作为轴承内圈的边界条件。

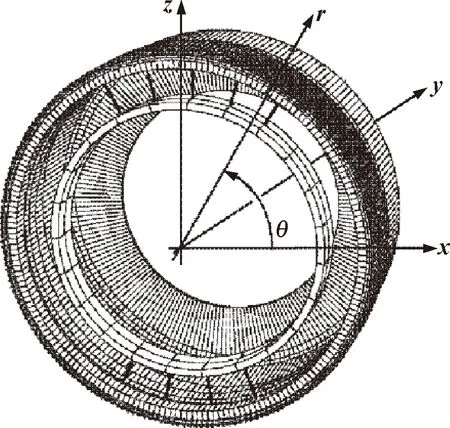
图3 谐波齿轮的简化模型

2 计算结果与分析

通过分析谐波齿轮传动系统中柔轮与刚轮之间插入的接触单元，可知在两轮间插入接触单元之前，两轮轮齿间有重叠；插入接触单元之后，两轮齿无重叠且接触平滑。

对柔轮长轴及其周围的变形情况进行研究，如图4所示，不考虑接触单元时柔轮的半径大于考虑接触单元时的半径。如果不考虑接触问题，则柔轮将自由变形而不受刚轮的约束。通过引入接触单元，柔轮的变形将受到刚轮的限制而变小，有接触单元时的变形量与实验结果吻合较好。图5所示为输入转矩为329 N·m时，柔轮长轴附近的应力分布情况。可知：在柔轮长轴左侧产生了较大的拉应力，而在右侧则出现了压应力，这是该类结构件的典型特征，与实验测量结果相吻合。随着波发生器的转动，柔轮的应力呈周期性变化，即拉应力到压应力呈对称性，这样很容易引起谐波齿轮系统的零件产生疲劳，并最终失效。在柔轮的开口部，拉、压应力都会达到最大值，该部位疲劳情况非常严重。

图4 柔轮长轴周围半径

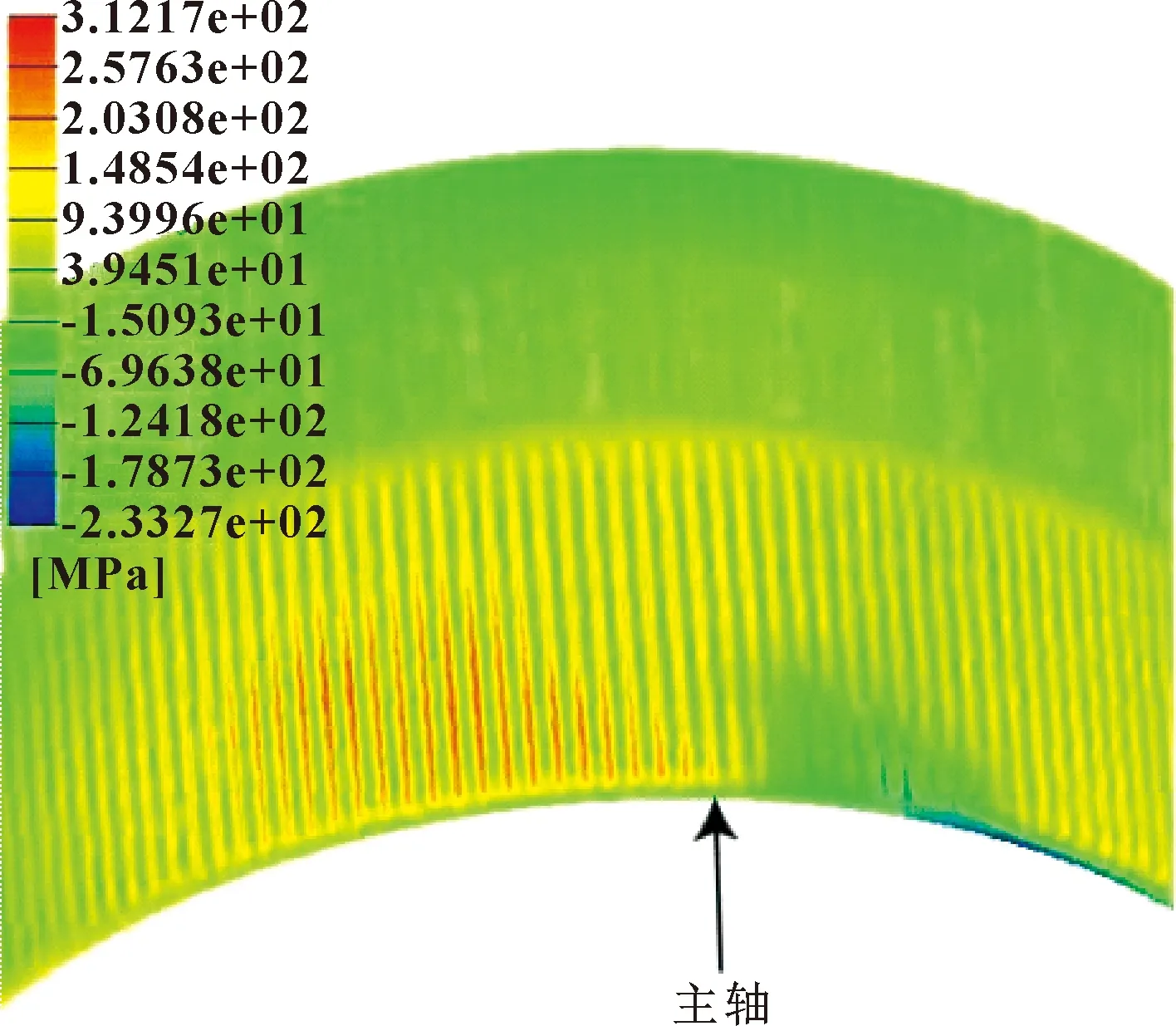
图5 柔轮的周向应力分布

图6所示为在柔轮上半部0～180°内，当输入转矩为329 N·m时，通过实验测量和数值计算所得的柔轮齿根部周向应力分布情况，其下半部的应力分布与图6对称。可知：实验测得的周向应力在柔轮长轴(角度为90°时)两边形成2个波峰，最大值大约为450 MPa，在110°线附近；而数值计算结果中，周向应力在110°线附近也有2个波峰，其最大值约为400 MPa，与实验结果很相近。这表明，有限元方法能够定量地估算柔轮的应力分布。

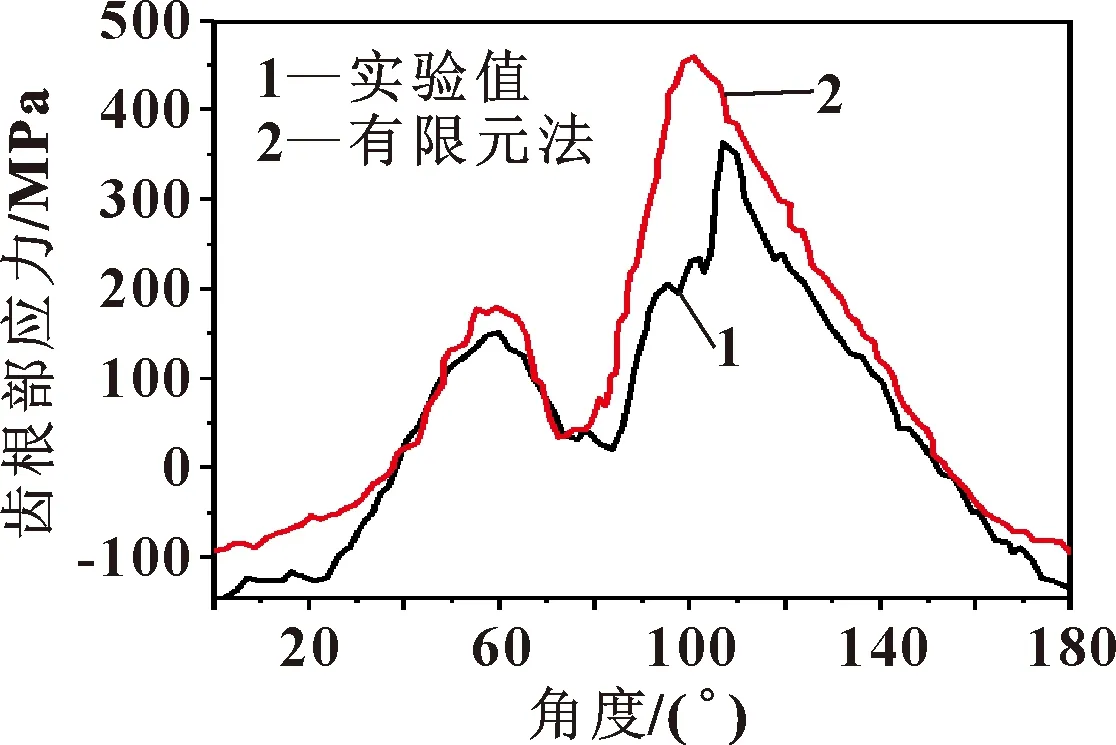
图6 柔轮轮齿根部的周向应力分布

采用同样的方法进行计算，发现当输入转矩增加时，所得到的柔轮齿根应力变化规律与图6所示的应力分布极为相似。当输入转矩达到极限值时，虽然此时的应力分布情况也很相似，但其应力值却有较大提升。在这种临界状态下，用实验的方法来测量柔轮齿根部的应力分布非常困难，然而用数值模拟的方法估算任意载荷下柔轮的应力状态却非常容易。