切换网络控制系统鲁棒H∞容错控制

赵千钧，付兴建

(北京信息科技大学，北京 100192)

0 前言

随着科学的发展、技术的进步，控制理论、计算机技术和现代网络通信技术迅猛发展，加上各学科领域之间的相互交叉渗透，使控制系统越来越复杂、被控对象越来越多元化。网络控制系统(NCS)得到了迅猛的发展，但网络的引入会带来网络诱导时延、数据丢包、量化、通信约束等问题。时延和丢包的存在不仅降低了系统的性能而且可能破坏系统的稳定性，因此，对网络控制系统时延和丢包的研究具有十分重要的理论和实际意义[1-2]。

由于数据传递过程中丢包现象的出现具有不确定性和难以预测性，所以对于丢包问题的解决具有相对复杂性。迄今为止，对于丢包问题的研究也取得众多成就。文献[3]中研究了带有随机丢包的基于采样数据T-S模糊网络控制系统的均方可镇定性问题。文献[4]中研究了双边丢包的系统，利用伯努利分布的相关知识提出满足观测器指数稳定的分析方法。文献[5]中为了减少网络通信对网络控制系统的影响，提出了一种在前向和反馈信道中具有随机丢包的网络无模型自适应预测控制方案。

近年来，网络控制系统的容错控制取得了一些研究成果[6-8]。文献[9]中针对不同的外部噪声类型,选取不同的性能指标,逐步深入地对分布时滞网络控制系统鲁棒控制器设计问题展开研究。文献[10]中研究了传统容错控制方法难以保证非线性系统在执行器和传感器多故障并发情形下的稳定性问题。

目前研究一般都分别针对执行器和传感器故障设计容错控制器以保障系统稳定[11]。然而在复杂的实际控制系统中, 多处执行器和传感器故障完全可能同时并存, 因此针对单一类型故障设计得到的容错控制器不一定能够稳定多类别故障并发系统, 存在较大安全隐患。文献[12]中考虑了状态不可测时一类网络切换系统的鲁棒H∞控制问题，针对既有传感器失效、又有执行器失效的故障情况，设计了一种无记忆状态反馈控制器。

本文作者针对含有数据丢包和时延的网络控制系统，将服从伯努利丢包的网络控制系统视为以一定速率切换的开关，建立了针对系统故障的数学模型。结合Lyapunov理论和异步动态系统理论以及状态反馈的有关知识，得出满足传感器和执行器均出现故障但仍能稳定运行的条件，并通过LMI工具箱计算出关于状态反馈的系数，设计出有效的具有鲁棒特性的容错控制器。通过算例仿真证明方法的可行性。

1 系统描述

1.1 含时延和丢包的NCS建立

首先考虑无丢包情况下的离散系统：

x(k+1)=Adx(k)+Bd0(τk)Kx(k)+Bd1(τk)Kx(k-1)

(1)

由于定义τk时延满足：

τk∈[τmin,τmax],0≤τmin≤τmax≤T

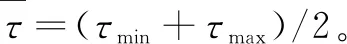
则:

Bd0(τk)=B0+D0F(τk)E0

(2)

同理可得：

Bd1(τk)=B1+D1F(τk)E1

(3)

其中：

现做如下假设:

(1)执行器和传感器同时发生故障。

(2)系统的采样周期为T,传感器使用时钟驱动方式，执行器与控制器都使用事件驱动的方式，将数据封装在单个数据包向网络进行传送。

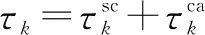
具有不确定时延的网络控制系统为

(4)

服从伯努利丢包的网络控制系统看作按一定速率切换的开关，将传感器和控制器的网络看作S1，控制器和执行器的网络看作S2。 具有时延和丢包的NCS结构如图1所示。

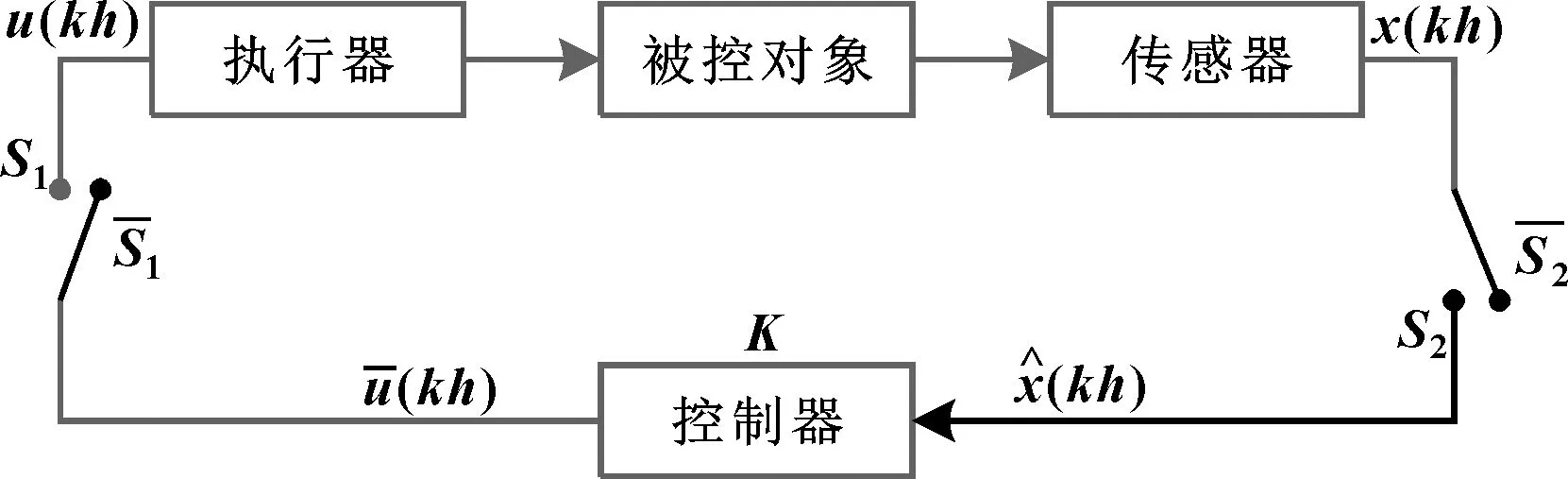
图1 具有时延和丢包的NCS结构

当开关在S1、S2时：

(5)

(6)

(7)

(8)

具有不确定时延和丢包的网络控制系统可描述为

Z(k+1)=φiZ(k)

(9)

其中：

1.2 多故障并发系统的建立

若系统有m个执行器，考虑执行器可能发生故障情况，引入开关矩阵L，并将其放在输入阵和反馈增益之间，其形式为L=diag{l1,l2,…,lm},其中:

式中:L∈Ω,Ω为执行器开关矩阵L的对角元素任取0或1的各种组合，表示所有可能的执行器故障模式的集合。

若系统有j个传感器，考虑传感器可能发生故障情况，引入开关矩阵G，并将其放在反馈增益和输入矩阵之间，其形式为G=diag{g1,g2,…,gj},其中:

式中:G∈Γ,Γ为执行器开关矩阵G的对角元素任取0或1的各种组合，表示所有可能的执行器故障模式的集合。

当执行器和传感器同时出现故障时，具有不确定时延和丢包的网络控制系统可描述为

(10)

其中：

2 容错控制器的设计

针对执行器和传感器故障并存时，不确定时延网络控制系统的鲁棒容错控制的目标是求得状态反馈增益矩阵K，使得闭环系统对于所有执行器和传感器故障并存在L∈Ω和G∈Γ，网络控制系统是渐近稳定的。为了得出验证结果，需要以下引理:

s=1,2,…,N。此异步动态系统是指数稳定的，衰减率为α。

引理2[13]:给定常数矩阵A、P、Q，当P=PT>0,Q=QT,就有ATPA+Q<0

当且仅当

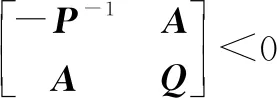
引理3[13]：当有适当维数矩阵Q=QT、H、E，则QT+HF(t)E+ETFT(t)HT<0要满足FT(t)F(t)≤I的F(t)都可以成立的充要条件是有正数ε>0使得下式成立：

Q+ε-1HHT+εETE<0

(11)

定理1：对于系统(10)，假设传感器到执行器及控制器到执行器的数据丢包率分别为r1、r2，对任意可能发生的执行器和传感器同时故障的情况L∈Ω、G∈Γ,若存在标量ε>0，矩阵T和正定对称矩阵X、Y、Z以及标量α1、α2、α3、α4满足：

(12)

(13)

(14)

(15)

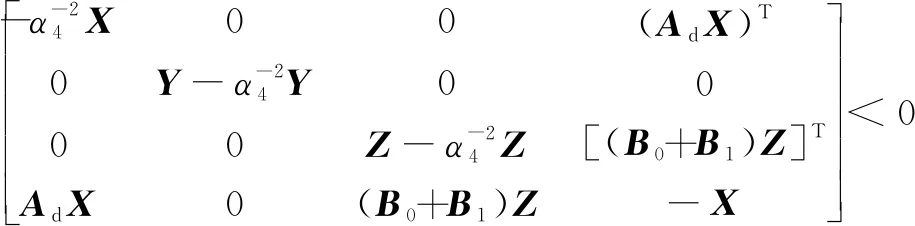
(16)

系统在执行器故障和传感器故障时可保持渐近稳定有一定的容错能力，状态反馈控制器为K=TX-1。

证明：构造Lyapunov泛函

uT(k-1)Ru(k-1)

其中:P和R均为正定对称矩阵。当开关在S1、S2时：

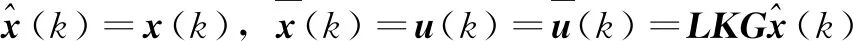
则:

D1FE1LKG)]x(k-1)+xT(k-1)[(B1LKG+D1FE1LKG)TP(Ad+B0LKG+D0FE0LKG)]x(k)+xT(k-

式中:

φ12=(B1LKG+D1FE1LKG)TP(Ad+B0LKG+D0FE0LKG)

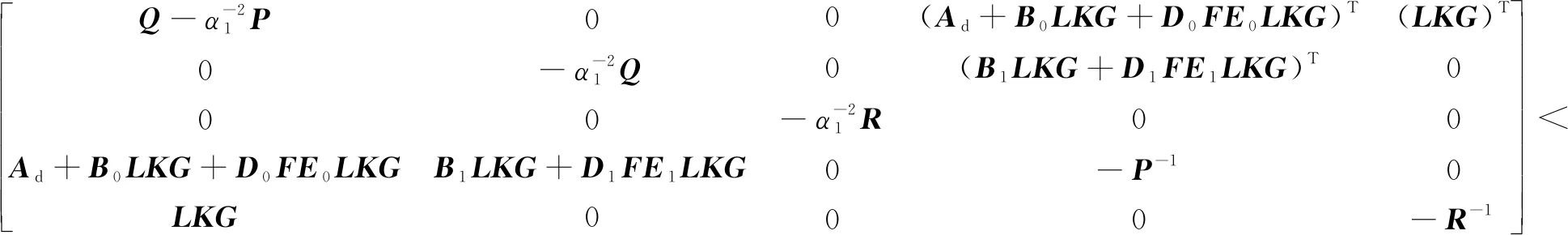
(17)

将F=F(τk)代入上式可得：

(18)

由引理2.2上面的式子等价于:

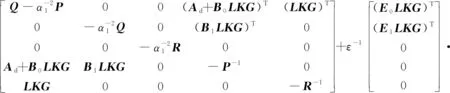
(19)

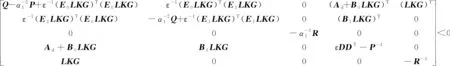
(20)

再一次对上面的式子应用引理2.2:

(21)

但是由于上式是非线性不等式，因此，要将其转化成线性不等式。在不等式的左右两端同时乘以一个具有对角化的矩阵，即diag{P-1,P-1,P-1,I,I,I}，令P-1QP-1=Y,T=KX,Z=R-1,P-1=X，得：

(22)

证毕。同理可证另外3个不等式。

3 算例仿真

考虑不确定NCS，参数的设定如下：

设采样周期T=0.05 s，时延τk∈[τmin,τmax]并取τmin=0,τmax=0.05，令数据传输成功率r1=0.900,α1=1.152 3,α2=0.980 0,λ=1.000,σmax[F(τk)]≤δ=0.030 6。

根据定理1，给定K=TX-1，取ε=1，运用LMI工具箱求得一组X、T的可行解，得到:

考虑表1故障类型,表中：数字1表示传感器2和执行器2同时出现故障的情况，数字2表示传感器1和执行器2同时出现故障的情况，数字3表示传感器2和执行器1同时出现故障的情况，数字4表示传感器1和执行器1同时出现故障的情况。下面对4种情况进行实例仿真。

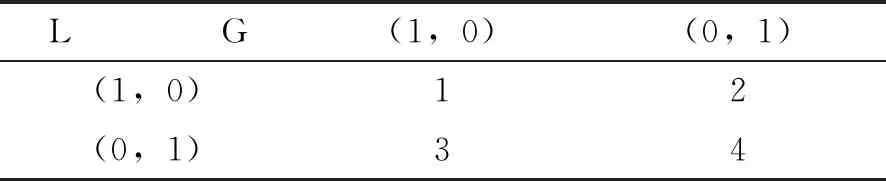
表1 故障类型

系统的状态响应仿真曲线如图2—图5所示。可以看出：状态x1和状态x2的响应曲线都能到达收敛，最终稳定并趋于零值，所以设计得到的NCS容错控制器具有很好的控制效果，可以使系统在收到不确定时延、数据包丢失以及传感器和执行器同时出现故障的情况下依然达到稳定的状态。

图2 基于故障类型1的状态响应曲线 图3 基于故障类型2的状态响应曲线

图4 基于故障类型3的状态响应曲线 图5 基于故障类型4的状态响应曲线

4 结束语

针对执行器和传感器同时失效的故障情况，建立了一类同时具有不确定时延和丢包的网络控制系统故障模型;通过Lyapunov理论和异步动态系统理论，对网络控制系统的鲁棒容错控制进行了分析，给出了控制系统渐近稳定的充分条件;并设计了鲁棒容错控制器，结合数值实例得到仿真结果，根据仿真结果验证了结论的合理性和可行性。