新课标下函数的教学策略研究

蒲志勇

(广东省中山市实验中学，广东 中山 528404)

一、熟读教材，理解编者目的

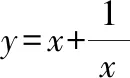
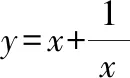
二、善于思考，创新教学模式

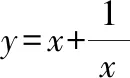
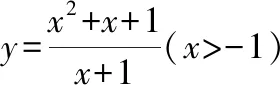
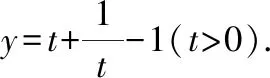
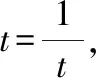
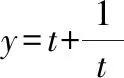
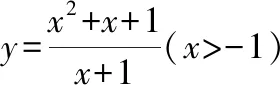
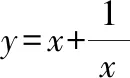
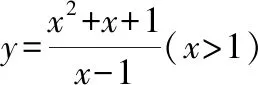
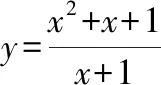
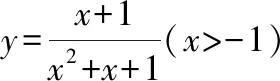
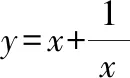
三、巩固精炼，有效综合练习

学生不能只学习书本的知识概念，必须要通过练习去加强自身对知识的理解与掌握练习是一个非常重要的环节如果学生只是学会了书本知识而不加以练习，那么对书本知识的理解不能长久记忆，是肤浅的、片面的所以，教师在知识学习后布置一定量的习题练习是非常必要的，而且布置什么样的练习也是很有学问的

1要建造一个容积为1200 m，深为6 m的长方体无盖蓄水池，池壁的造价为95元m，池底的造价为135元m，如何设计水池的长与宽，才能使水池的总造价控制在7万元以内(精确到01 m)？

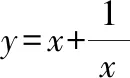
(1)求,,的值

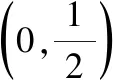
该题相对前一题适用性弱一些，理论性较强，体现出数学的理论研究特点该题既是对函数基本知识的练习(待定系数法求参数和奇偶性的应用)，也是对数学严密逻辑推理的训练，比如第二问的证明，可以让学生进一步学会结合专门的数学术语用定义去证明问题，有利于提升学生思维的严密性和逻辑推理能力

四、知识提升，拓宽学生视野

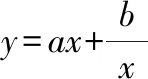
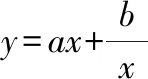
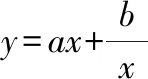
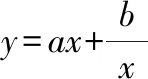
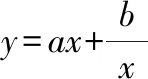
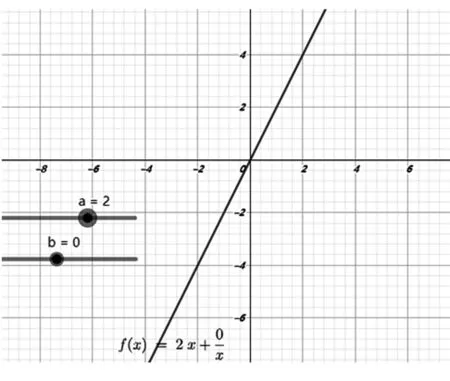
图1

图2

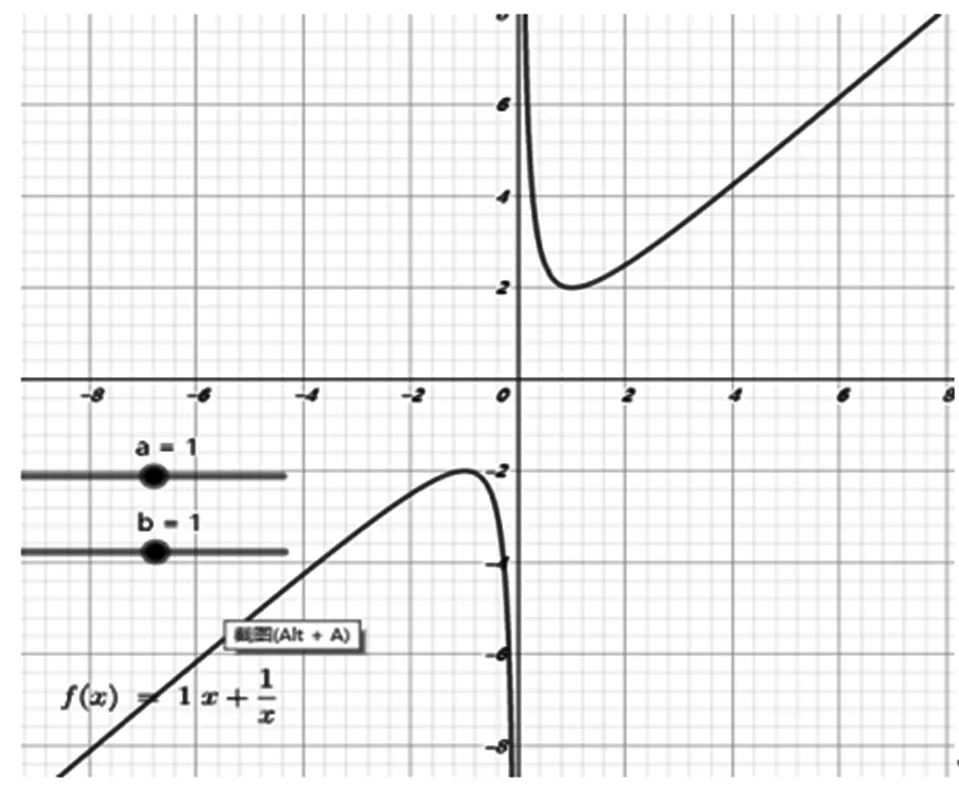
图3

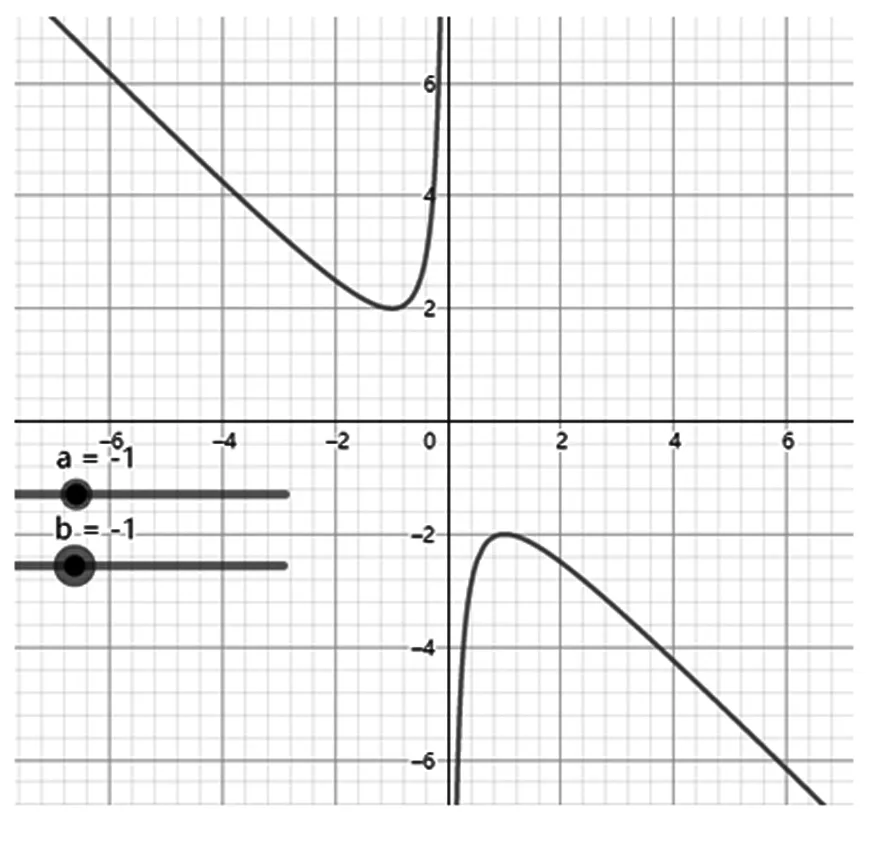
图4

首先，由图像可得到函数定义域、值域、奇偶性、单调性、对称性、最值等其次，改变参数，的值，观察函数的图像形状和变化情况，得出相应性质最后，观察函数图像，注意函数分别在哪些位置取到最小值和最大值，特别是借助基本不等式确定取到最值时相应的值

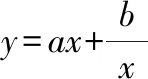
1定义域：{|∈,≠0}；

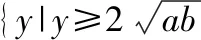
3图3、图4呈“对勾”形状，是中心对称图形(关于原点对称)，是奇函数，可进一步用(-)=-()检验；

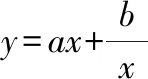
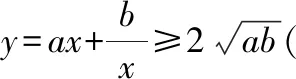
当<0时，其性质可仿照>0得到

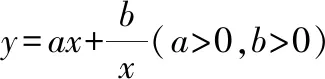
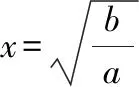
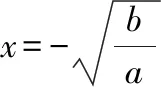
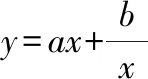
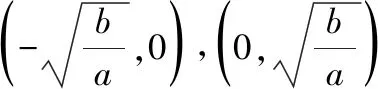
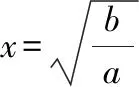
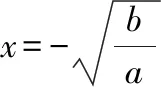
互动交流：当,同号时，虽然我们也可以通过函数的解析式判断它的定义域、奇偶性，但是从图像上可以更加直观地发现这些性质，特别是最值与单调区间由图像更加容易得到，当然要借助基本不等式来求得准确的最值点和最值，这也进一步体现出数形结合的魅力——数缺形时少直观，形缺数时难入微！

以上的研究都是在,同号的情况下进行的，教师可结合学生实际，引导其继续探索>0,<0或<0,>0的情况，让学生感受数形结合的魅力我们借助数学软件画图进行研究，可以让问题变得直观、简单如图5、图6

图5

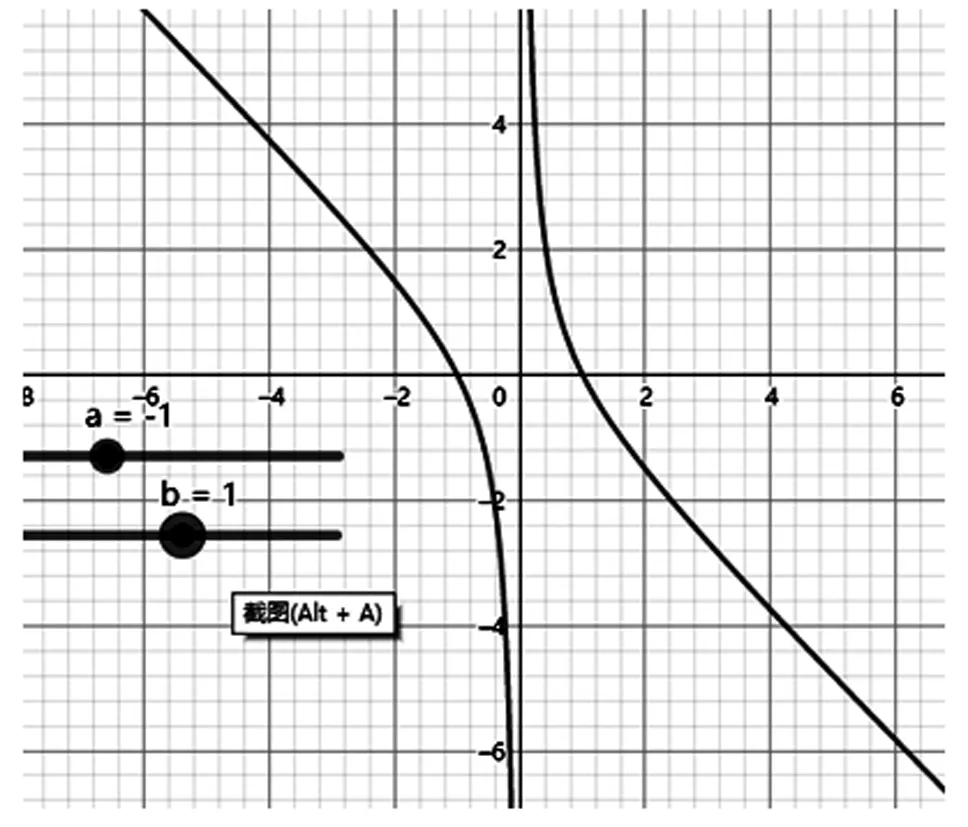
图6

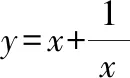
本研究为学生进一步学习提供了必要的数学准备，且使得不同层次的学生在数学上得到不同的发展，为学生提供多层次、多种类的选择，促进学生个性化的发展教师应倡导积极主动、勇于探索的学习方式，让学生动手实践、自主探索、合作交流，使学习过程成为“再创作”的过程学生体验发现知识和创新解法的历程，有利于发展自身的创新意识，也有利于提高自身的数学思维能力，以及直观感知、观察发现、归纳类比、抽象概况、反思与体系建构等思维过程教师应发展学生的数学应用意识，注重数学活动过程，注重数学思想方法教学，让学生体会其在后续学习中的作用此外信息技术的应用使得数学问题可以用图形的和符号的方式进行表达、解决，并在这些表示方式间进行转换，形成更多的解决问题的方法，使学生逐渐成为更加主动的学习者，形成更高级的概念与能力