分式函数最值的多种求法
2017-09-03西安高新第三中学710075吕二动
西安高新第三中学(710075) 吕二动
分式函数最值的多种求法
西安高新第三中学(710075) 吕二动
分式函数的最值题型是多样的,因而求分式函数的最值的方法是多样的.本文主要总结了函数(a,b,c,d,m,n均为常数,且ad>0,的最值的各种求解方法.
分式 函数 最值
求分式函数最值的方法很多,从不同角度入手,则可得到不同的解法,本文主要从不等式法、判别式法、构造等差数列法、代换法、向量法、求导法、构造图形模型法的思想出发,得到下列的各种解法.
一.不等式法
解法一均值不等式法(课本必修五的知识)

①当a, d 与m, n 同号时, a(c−dx) > 0, d(ax+b) > 0,由ac + bd > 0, 故
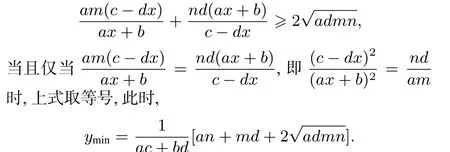
②当a, d 与m, n 异号时, a(c−dx) < 0, d(ax+b) < 0,由ac + bd < 0, 故


解法二柯西不等式法( 课本选修4-5 的知识)

①当a,d与m,n同号时,a(c−dx)>0,d(ax+b)>0 md>0,an>0,由ac+bd>0,

②当a,d与m,n异号时,a(c−dx)<0,d(ax+b)<0 md<0,an<0,由于ac+bd<0,
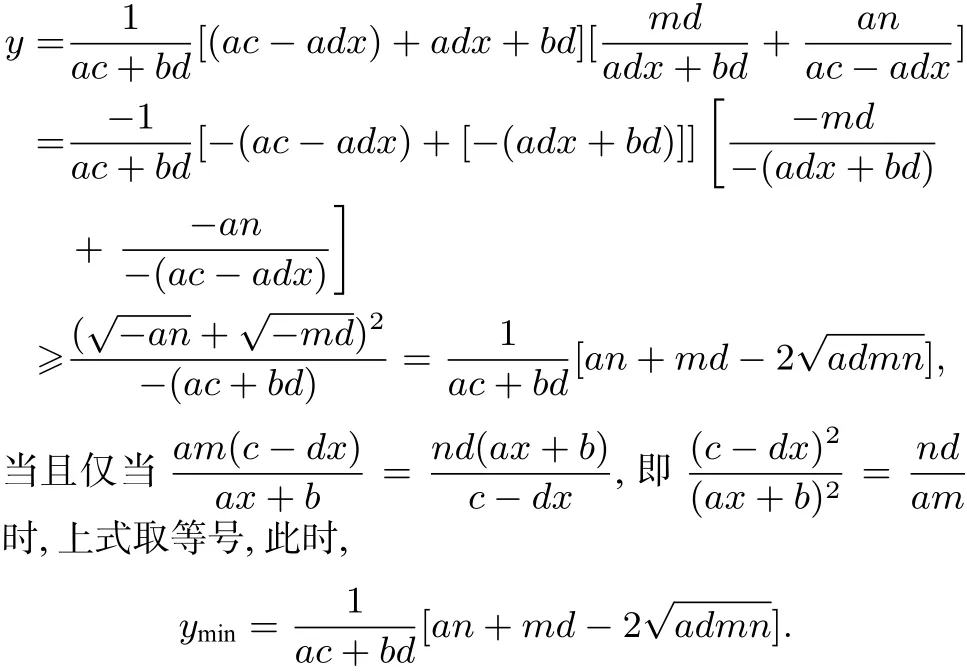
二、判别式法
解法三 (函数值域的方法)

由于

①当a,d与m,n同号时,a(c−dx)>0,d(ax+b)>0,由于ac+bd>0,又y>0,从而t>0.故

三.构造等差数列法


②当a,d与m,n异号时,a(c−dx)<0,d(ax+b)<0,因为ac+bd<0.又y>0,所以t<0.从而
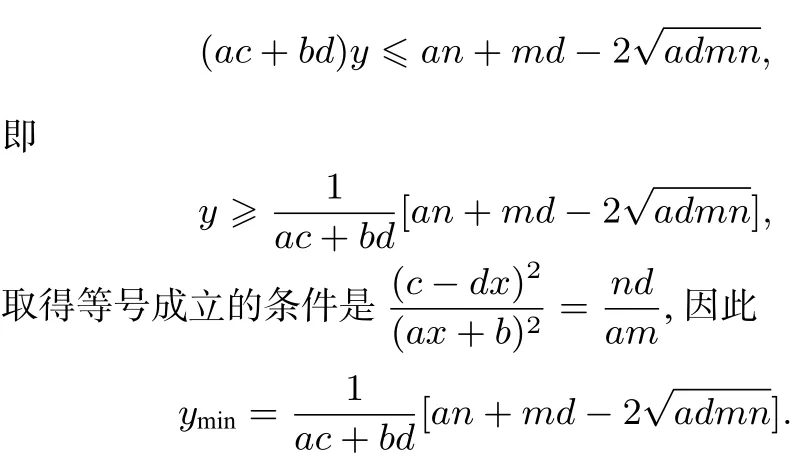
四.代换法
解法五 三角代换法,课本必修四知识

①a,d与m,n同号时,md>0,an>0,故ac+bd>0.所以
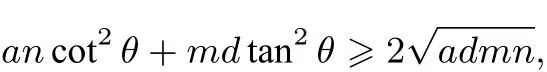

②当a,d与m,n异号时md<0,an<0,所以ac+bd<0.所以
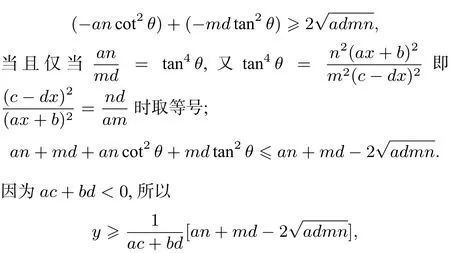
所以

解法六 整体代换法,课本必修五的方法

①a,d与m,n同号时,md>0,an>0,所以ac+bd>0.因为p>0,q>0,所以

解法七 局部代换法,课本必修四的方法

①a,d与m,n同号时,md>0,an>0,所以ac+bd>0.因为p,q,同号,所以
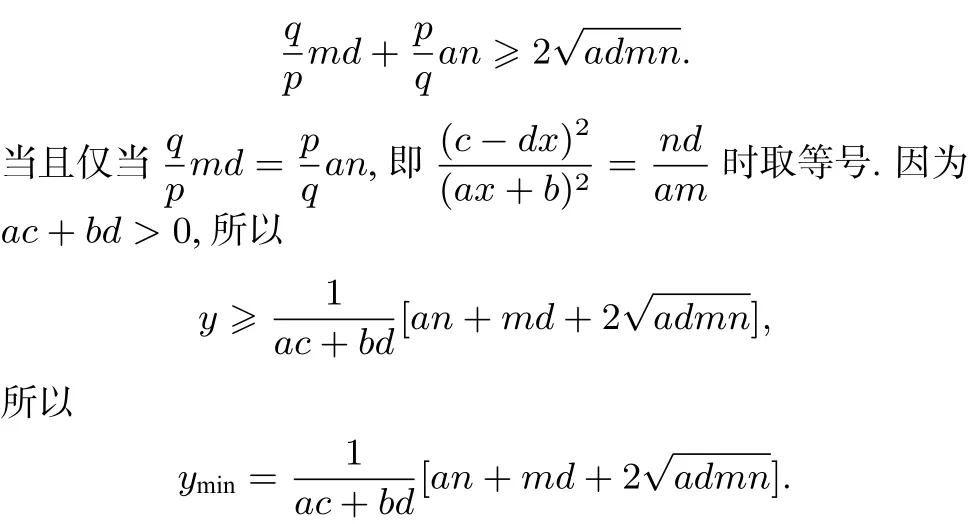
②a,d与m,n异号时,ma<0,dn<0,所以ac+bd<0.因为p,q,同号,所以

五.向量法
解法八 课本必修四知识
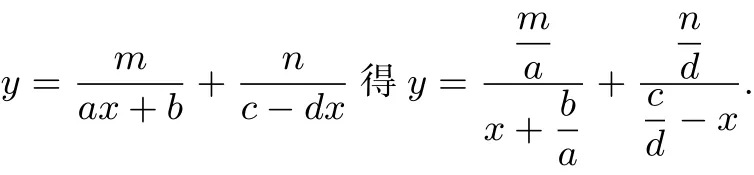


六.导数法

①a,d与m,n同号时,ma>0,dn>0,所以ac+bd>0.令 y′=0得即

②a,d与m,n异号时,ma<0,dn<0,所以ac+bd>0.令 y′=0得即得


七.构造图形模型法
解法十 (课本选修2–1的方法)
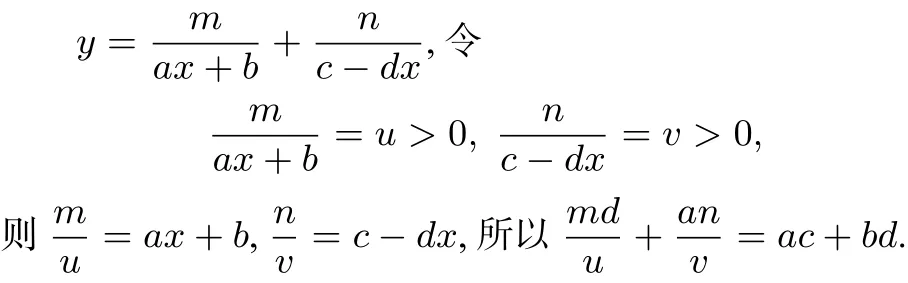
①a,d与m,n同号时,md>0,an>0,所以ac+bd>0.所以所以则


可化为

所以∆=[(an−dm)−(ac+bd)y]2−4(ac+bd)dmy=0.
所以[(an+dm)−(ac+bd)y]2=4admn> 0,所以所以

所以
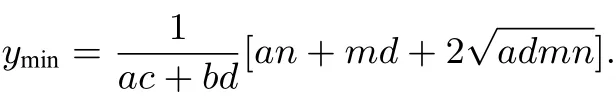
②a,d与m,n异号时,md<0,an<0,所以ac+bd<0.所以则

问题转化为关于u,v的方程组

在条件

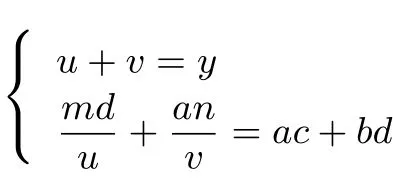

图1
可化为(ac+bd)u2+[(an−dm)−(ac+bd)y]u+dmy=0.所以∆=[(an−dm)−(ac+bd)y]2−4(ac+bd)dmy=0.所以[(an+dm)−(ac+bd)y]2=4admn> 0,所以(ac+bd)y−(an+dm)=−所以

所以

以上各种解法的解题角度各不相同,从而各种解法有自己的巧妙和独特之处,都能达到解题目的,同时也可以锻炼思维能力,在学习过程中会所帮助.
