热环境下纤维增强复合材料圆柱壳非线性振动分析与验证
2022-10-12李晖吕海宇邹泽煜罗忠马辉韩清凯
李晖,吕海宇,邹泽煜,罗忠,马辉,韩清凯
1.东北大学 机械工程与自动化学院,沈阳 110819 2.东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819
纤维增强复合材料圆柱壳广泛应用于航空、航天、船舶等领域,由于该类型结构很多都服役在高温、强振动、冲击等恶劣工况下,极易发生动态响应超标、基体裂纹、纤维断裂、分层失效等问题,因此有必要研究其动力学建模、试验和性能优化方法与计算。
多年来,人们对复合材料圆柱壳在常温环境下的非线性振动问题开展了富有成效的研究。如Iu和Chia采用修正的Donnell非线性壳体理论,在引入von-Kármán几何大变形假设后,研究了随激励幅值变化的复合材料圆柱壳非线性共振频率的求解方法。何建国等应用全拉格朗日列式法求解了加筋叠层圆柱壳的非线性频率,并研究了运动稳定性问题。Lakis等利用Sanders-Koiter非线性壳体理论推导了层合圆柱壳自由振动运动方程,并采用有限元法验证了模型的正确性。Amabili提出了Amabili-Reddy高阶剪切变形理论,通过数值方法研究了层合圆柱壳的非线性振动响应。宋旭圆建立了弹支边界下考虑几何大变形影响的复合材料圆柱壳非线性振动分析模型。张悦等考虑了硬涂层材料的应变依赖关系,并推导获得了硬涂层圆柱壳非线性强迫振动的解析公式。李晖等提出了螺栓松动边界下具有振幅依赖性的复合材料圆柱壳非线性共振频率和动态响应的求解方法。
只有少数科研工作者对热环境复合材料圆柱壳的非线性振动问题开展了研究。Malekzadeh和Heydarpour考虑了温度导致的材料非线性,建立了热环境旋转功能梯度圆柱壳自由振动的解析模型。基于Reddy高阶剪切变形理论,Zhang等考虑热效应造成的材料非线性影响,求解了碳纳米管增强复合圆柱壳在冲击载荷作用下的动态响应。Yang等考虑了温度效应的影响,研究了碳纤维增强聚合物基层合圆柱壳的1∶2内共振问题,求解获得了非线性共振频率、频响曲线和分叉图。Sheng等考虑温度导致的材料非线性和von-Kármán几何大变形的影响,建立了热环境下功能梯度复合圆柱壳的非线性振动模型,并获得了非线性共振频率和频域响应。沈慧申等基于高阶剪切变形理论和von-Kármán几何大变形原理等建立了热环境下功能梯度和碳纳米管增强复合材料圆柱壳结构的非线性动力学模型,并预测了考虑温度依赖性的频率和动态响应参数。
在上述文献调研中,并未发现同时考虑几何非线性和材料非线性且在基础激励载荷作用下研究复合材料圆柱壳结构热振问题的相关报道。此外,对该类壳体结构开展热振试验研究的也不多见。针对上述问题,本文在考虑温度效应导致的材料非线性和von-Kármán几何大变形的基础上,建立纤维增强复合材料圆柱壳在均匀热环境下的非线性振动模型,并开展实验验证研究。
1 理论建模
1.1 模型描述
建立图1所示的纤维增强复合材料圆柱壳的理论模型,其处于悬臂边界条件,受到基础振动激励载荷的作用。首先,将其中面作为参考平面,建立坐标系,假设、、为沿方向的位移分量,壳体长为,中面半径为,厚度为,每层位于坐标轴较低表面-1和较高表面之间,每层的厚度均相同。1、2和3分别代表纤维的主轴方向,且“1”方向与轴方向的夹角为,假设复合材料圆柱壳平行纤维方向的弹性模量为,垂直纤维方向的弹性模量为,1-2平面内的剪切弹性模量为,、和为不同方向的损耗因子,和为相应的泊松比。

图1 热环境下纤维增强复合材料圆柱壳理论模型Fig.1 Theoretical model of fiber reinforced composite cylindrical shell in thermal environment
1.2 材料非线性假设
考虑温度效应影响,可将复合材料圆柱壳的非线性材料参数表示为
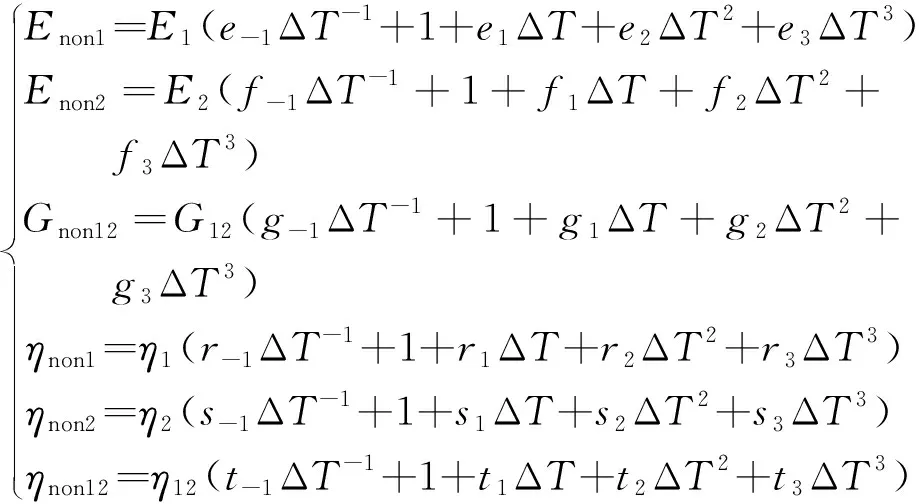
(1)
式中:、和为不同温度下的弹性模量(包括拉伸模量和剪切模量);、和为不同温度下的损耗因子;、、、、和为与温度有关的非线性材料参数的拟合系数,=-1,1,2,3;Δ为温度变化量。
考虑振幅依赖性的影响,基于应变能密度函数法可将结构的非线性材料参数表示为

(2)


(3)

1.3 考虑几何非线性影响的圆柱壳理论
考虑几何非线性的影响,根据Love壳体理论,基于von-Kármán几何大变形假设将圆柱壳任意一点的应变-位移的关系表示为

(4)


(5)
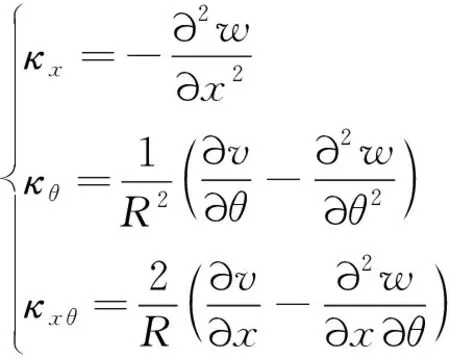
(6)
考虑热环境的影响,复合材料圆柱壳产生的热应变为

(7)

在热环境下圆柱壳结构的第层应力-应变关系为
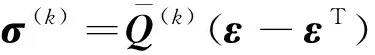
(8)
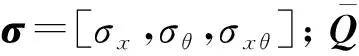
各个方向对应的内力=[,, ]和内力矩=[,, ]对应的向量可表示为

(9)
将式(11)代入式(12)可得

(10)
式中:、和分别为拉伸、耦合与弯曲矩阵元素。

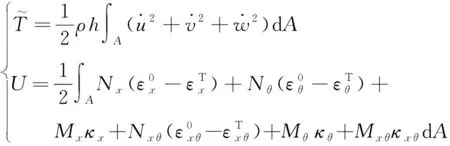
(11)
式中:为密度;为相应的积分区域面积。
结构受到的基础振动激励可等效为均布惯性力作用,即

(12)
式中:、和分别为激励沿轴向、周向和径向的分量;、和为激励幅值;为周向波数;为激励频率;为时间变量。
结构所受惯性力做功为
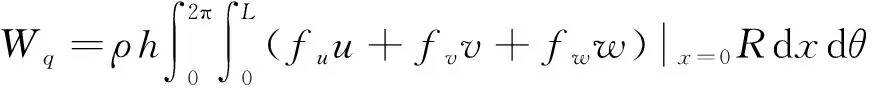
(13)
1.4 非线性振动特性求解
应用Ritz法可得复合材料圆柱壳位移场函数:

(14)


然后定义能量函数为

(15)

将能量函数对各里兹Ritz求偏导:

(16)
式中:、和为里兹系数;为最大截断系数。
可获得热环境下结构的振动微分方程为
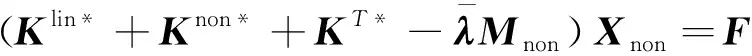
(17)

求解热环境下的固有频率和振型,只需令材料阻尼矩阵和激振力向量为,即

(18)

为保证式(20)有解,需要系数矩阵的行列式为0,即

(19)

复合材料圆柱壳结构无阻尼圆频率和材料损耗因子可表示为

(20)
式中:为复合材料圆柱壳在热环境下对应于某一阶周向波数和轴向半波数的无阻尼固有圆频率,即=。
热环境下复合材料圆柱壳的阻尼比可表示为

(21)

为求解复合材料圆柱壳的振动响应,根据空间与时间变量分离法,将其位移场函数进一步假设为

(22)
式中:()为时间有关的位移场分量。
复合材料圆柱壳的强迫振动响应可用Duhamel积分写成一般形式:

(23)


sin()
(24)
式中:为激振力。
最后,将式(22)经傅里叶变换操作和卷积运算即可得到结构的频域振动响应。
2 实验验证
2.1 测试对象和系统
分别对两个CF120碳纤维/环氧树脂圆柱壳试件进行测试,将其命名为试件I和试件II,其长度、半径、厚度分别为130 mm×65 mm×3 mm和150 mm×125 mm×3 mm,铺设参数为[(0°/90°)],材料参数见表1,其中和分别为平行与垂直纤维方向上的热膨胀系数,为试件的泊松比,纤维体积分数约为45%。图2为建立的热振测试系统,其中激励系统由波形发生器、联能JZK-100电磁激振器、联能YE5878功率放大器组成,通过夹具和激振平台为壳体试件提供可控的基础振动激励(其幅值可通过Endevco 6240M10高温加速度传感器反馈);温控系统包括一个带有耐热玻璃窗的加热箱和一个长白T-500温度控制设备,使圆柱壳试件处于均匀的热环境中(内置有PT100热电偶传感器可精确控制温度);试件的振动响应可通过Polytec PDV-100激光测振仪经由45°反射镜改变光路后获得,所测的振动和温度信号均通过LMS数据采集仪和PC终端进行记录和查看。
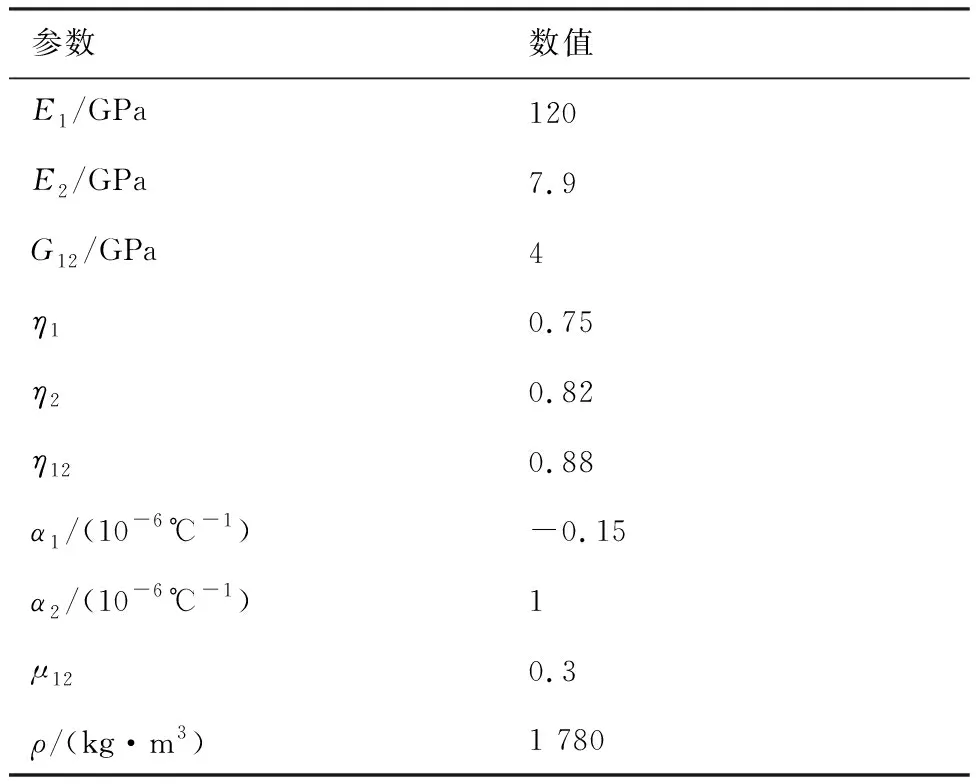
表1 CF120碳纤维/环氧复合材料圆柱壳在常温下的材料参数

图2 热环境下复合材料圆柱壳试件振动测试系统Fig.2 Vibration test system for composite cylindrical shells in thermal environment
2.2 非线性材料参数辨识
分别在20、50、150 ℃环境下通过扫频测试方法获得试件I在不同激励幅值下的共振频率和阻尼比数据,将这些测试数据输入MATLAB编写的迭代求解程序中,分别构造理论计算相对于上述测试数据的最小二乘相对误差函数(包括频率误差函数和阻尼误差函数)。以常温环境下的材料参数为基准,在上下浮动30%范围内以排列组合的方式分别对弹性模量和损耗因子进行迭代,当求解获得的共振频率和阻尼比对应的和分别取得最小值时,对应的不同温度和激励幅值下输入的材料参数即是辨识结果。表2和表3给出了考虑振幅和温度依赖性的CF120碳纤维/环氧树脂弹性模量和损耗因子辨识结果,结合提出的材料非线性假设关系式可通过数据拟合方法确定式(4)中的拟合系数,如表4所示。在此基础上,便可通过第1节中建立的该类型复合材料圆柱壳的解析模型实现对不同温度和激励幅值下结构非线性振动的分析与预测。

表2 考虑振幅和温度依赖性的CF120碳纤维/环氧树脂的弹性模量

表3 考虑振幅和温度依赖性的CF120碳纤维/环氧树脂的损耗因子Table 3 Loss factor of CF120 carbon fiber/epoxy resin with consideration of amplitude and temperature dependence

表4 非线性材料参数的拟合系数
2.3 测试与理论结果对比分析

从图3可知在不考虑材料和几何非线性问题的情况下,前三阶共振频率的最大计算误差达8.8%,而提出的理论模型在考虑上述非线性特征后,预测的共振频率与实测结果变化趋势一致,且最大计算误差仅为1.2%。另外在不同的温度下,由于材料非线性(导致共振频率减少)和几何非线性(导致共振频率增大)的共同影响,随激励幅值增大,结构第一、二阶共振频率呈先减少后增大的变化趋势,但由于高阶振动幅值较小(几何大变形效应不明显),因而第三阶共振频率呈逐步降低但下降趋势越来越慢的变化。
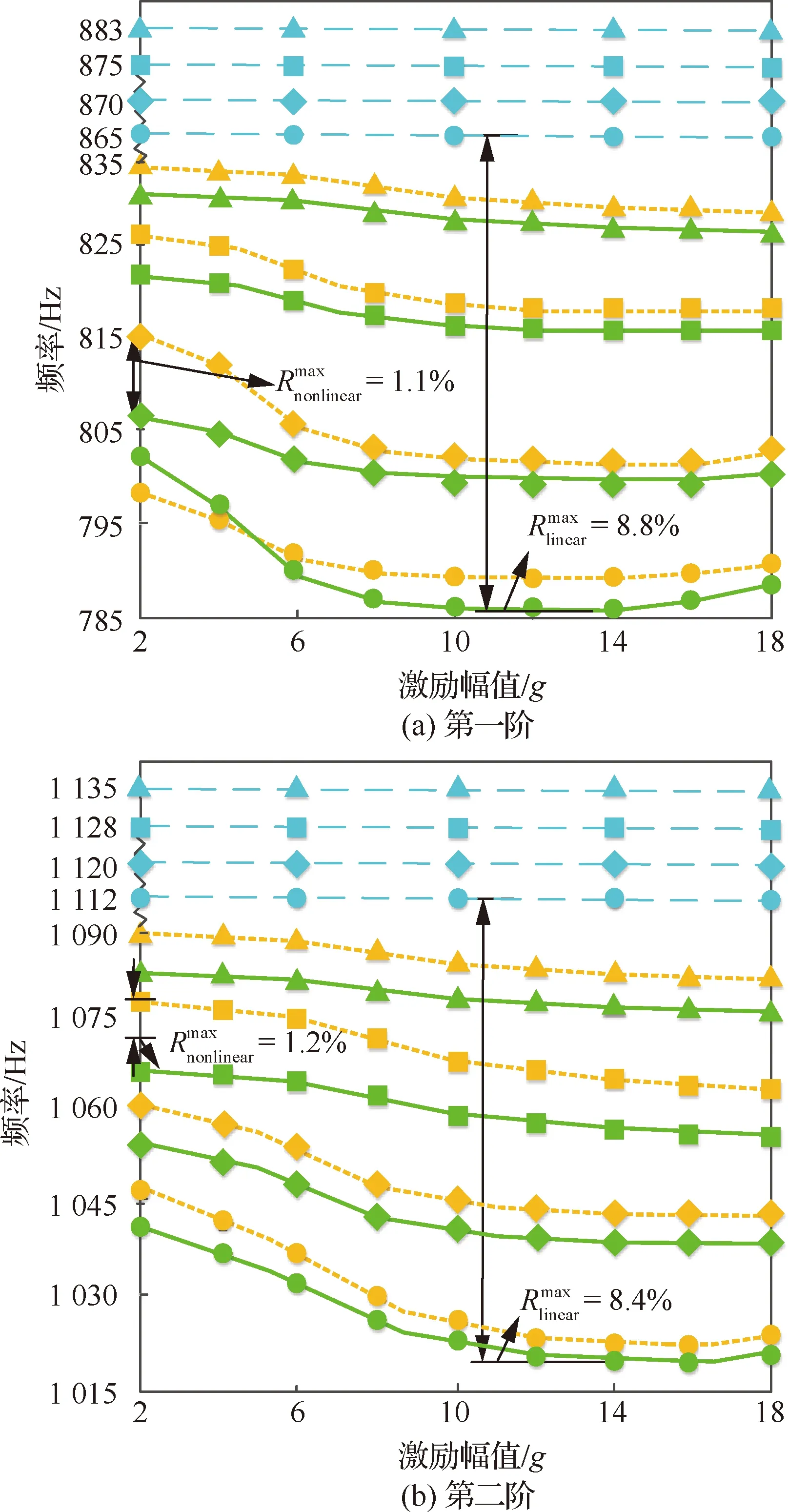
图4给出了实测和计算获得的非线性阻尼结果,分析可知结构阻尼比会随激励幅值和温度的提高而逐步增加。其中线性模型的最大理论计算误差达28.2%;而在考虑材料和几何非线性问题后,由提出的理论模型获得的阻尼结果与实测值吻合较好,最大计算误差为4.7%。

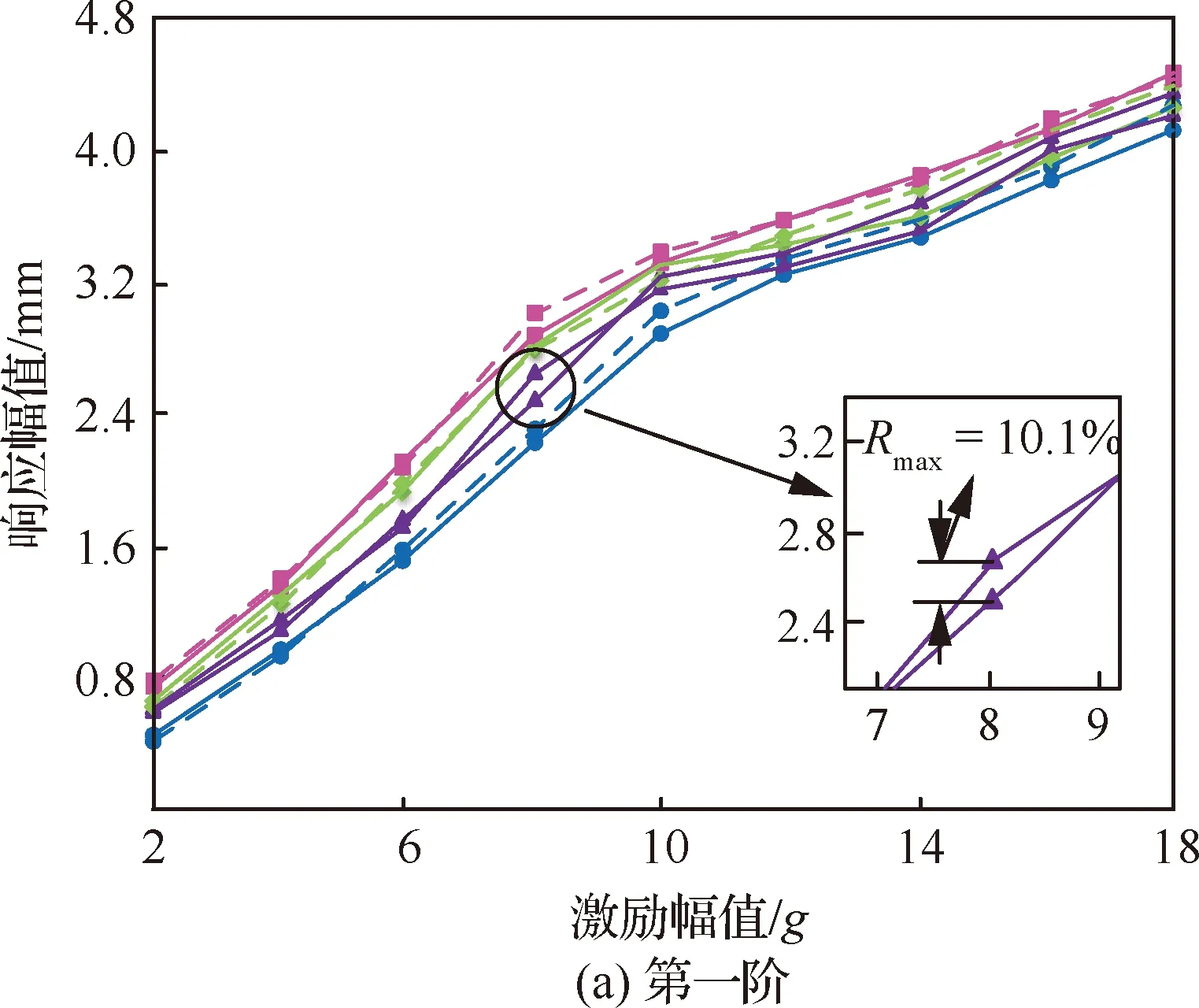
图5给出了实测和计算获得的非线性共振响应结果,其中为理论模型最大计算误差。对图5进行分析可知随激励幅值和温度的提高,共振响应幅值呈现逐步上升的趋势,提出的理论模型最大计算误差为10.8%。需要说明的是,虽不断增大的阻尼会对结构共振发挥一定程度的抑制效果,但由于外激励幅值增大和环境温度上升导致的“刚度软化”(弹性模量随温度上升而下降)对共振响应发挥了主导作用,因而共振相应幅值呈现不断上升的趋势。
3 结 论
建立了热环境下纤维增强复合材料圆柱壳的非线性振动模型,并利用热振测试系统开展了一系列实验测试研究,通过对比理论与实验结果发现:
1) 理论计算获得的结构在不同温度和激励幅值下前三阶模态的非线性共振频率、阻尼比和共振响应的最大误差分别为1.2%、4.7%和10.8%,属于误差允许的范围内,因而可证明理论模型的有效性。
2) 在不同的温度下,由于材料非线性和几何非线性的共同影响,随激励幅值的增大结构低阶共振频率呈先减小后增大的变化趋势,但由于高阶振动幅值较小,所以第三阶共振频率呈逐步降低但下降速度越来越慢的变化趋势。
3) 随激励幅值和温度的上升,复合材料圆柱壳结构各阶阻尼比和共振响应幅值均呈现出上升的趋势。
建立的解析模型和相关热振实验系统为研究复合材料圆柱壳的非线性振动问题提供了一种有效的理论模型和测试手段。
