面向测控数传资源一体化场景的卫星地面站资源多目标优化方法
2022-10-14孙刚彭双陈浩伍江江李军
孙刚,彭双,陈浩,伍江江,李军
国防科技大学 电子科学学院,长沙 410073
人造卫星具有作用范围广、持续时间长且不受国界地形限制等独特优势,已广泛应用于科学研究、经济社会发展以及军事等诸多领域。卫星的跟踪、测量、控制以及有效载荷数据的下传等操作离不开卫星地面站的支持,通常,将执行卫星的跟踪、测量以及控制操作的任务称为测控任务,以实现卫星的轨道测量、轨道机动及姿态控制;将执行卫星有效载荷数据下传的任务称为数传任务,数据经处理后形成数据产品,以实现卫星的价值。长期以来,由于受技术条件限制,地面站测控设备只能支持测控任务,数传设备也只能支持数传任务,二者不具备兼容性,无法实现对测控任务和数传任务的相互支持和同步执行,在一定程度上制约着地面站设备资源的利用效率。此外,随着航天事业的迅速发展,在轨卫星数量不断增多,使得在星地通信中本就相对匮乏的地面站资源更加捉襟见肘,而卫星地面站的建设、运行及维护又需要较高的成本投入。
针对星地通信中地面站资源相对匮乏的问题,着眼于资源调度优化性,国内外的相关机构和学者开展了大量卓有成效的研究。目前,用于卫星地面站资源规划问题常用求解算法包括:整数规划算法、基于图模型的搜索算法以及智能优化算法。由于卫星地面站资源规划问题是一类典型的NP-hard问题,具有较高的复杂度,使得整数规划算法无法适用于大规模规划场景;基于图模型的搜索算法通常会转化为寻径问题,算法的效率和优化性在很大程度上取决于搜索策略的设计;智能优化算法基于物理或生物学现象和行为建立启发元信息引导搜索进程,具有很强的通用性,在求解卫星地面站资源规划问题中得到广泛应用。此外,随着在轨卫星数量的不断增加,地面站资源规划问题的规模也随之增大,卫星管理机构关注的优化目标也呈现出多元化特征。进化多目标优化算法(Multi-Objective Evolutionary Algorithm, MOEA)是解决多目标优化的主流智能优化算法,近年来得到研究者的广泛关注,尤以NSGA-II为最;此外,以决策者偏好信息引导MOEA优化进程的偏好多目标进化算法(Preference-based Multi-Objective Evolutionary Algorithm, PMOEA)是当前进化计算领域的研究热点,偏好信息的引入提升了多目标优化问题求解的优化性和针对性。MOEA以及PMOEA在卫星地面站资源规划中的应用也有相关报道。
近年来,随着电子技术的发展,地面站测控设备与数传设备逐渐趋同,呈现出功能一体化的特性(即同一设备可分时或同时执行卫星的测控任务和数传任务),称之为地面站资源的测控数传一体化特性。由于在测控数传一体化规划场景下,测控任务和数传任务可共享所有地面站设备资源,且同一卫星的测控任务和数传任务可同步执行,因此可较大地提高地面站设备资源的利用率,进而缓解星地通信中地面站资源相对匮乏的现实难题。具体而言,其优势主要表现在以下几个方面:一是在实施任务规划过程中,任务对于地面站设备资源的选择具有更高的自由度,从而降低由于任务间冲突导致的任务取消或者任务时长缩减;二是可以从全局角度对测控任务和数传任务进行规划,从而达到更好的全局优化效果;三是可以将同一卫星的测控任务和数传任务规划至同一地面站设备的同一个时窗内,使得二者同步实施,从而达到节约资源、事半功倍的效果。但是,传统的卫星地面站资源规划方法只适用于测控资源规划或者数传资源规划的情形,并没有考虑二者趋于功能一体化的发展趋势,导致在处理测控数传资源一体化场景时只能分阶段进行规划,资源利用率低下,且规划结果的全局优化性也难以保证。目前,鲜有针对测控数传资源一体化场景下的卫星地面站资源规划方法的相关研究报道,论文拟针对该问题建立多目标优化模型并进行求解,设计了任务冲突时长最小化、天线负载均衡度最大化以及任务集聚度最大化3个独立的优化目标,其意义在于:一是在工程实践中,对于存在冲突无法正常执行的任务并不单纯取消,而是采用缩减任务执行时长的方法以使得任务能够部分执行,故最小化任务冲突时长的优化目标更符合工程实践需要;二是在地面站设备高负载运行的情况下,最大化天线负载均衡度的优化目标能够使得设备间的负载相对均衡,以达到延长设备整体使用寿命的目的;三是最大化任务集聚度能够使得规划结果中的任务在设定的任务集聚区间内分布相对聚集,区间外部的任务分布相对稀疏,以便于卫星管理机构执行例行设备维护操作或者避开某些执行任务的高风险时段。
综上所述,面向测控数传资源一体化场景的卫星地面站资源规划是一个复杂约束条件下的多目标组合优化问题,与传统的卫星地面站资源规划问题相比,其难点主要体现在以下方面:首先,测控数传资源一体化特性使得问题性质更为复杂,如何合理准确抽象数学模型是难点之一;其次,多维组合优化问题具有更广泛的解空间,而帕累托支配排序选择方式的选择压力随维度的增加骤降,导致优化性不易保证,如何合理设计启发式算子或引导机制以保证算法的优化性是难点之二。本文的主要贡献在于:
1) 根据测控数传资源一体化场景下的卫星地面站资源规划问题特征和工程实践需求,建立涵盖最小化任务冲突时长、最大化天线负载均衡度以及最大化任务集聚度的多目标约束满足问题模型。
2) 提出一种基于切比雪夫距离的膝点(Knee Point)定义方法,构建KG-NSGA-II-TTC&DT(Knee Guided Non-dominated Sorting Genetic Algorithm-II oriented integration of TT&C resources and Data Transmission resources)算法求解约束满足模型以获取在优化目标上的最佳折衷解。该算法在迭代过程中以帕累托前沿(Pareto Front, PF)中的膝点为参考引导算法进程以提高算法的优化性;同时,针对优化目标设计负载均衡算子、任务集聚算子以及迭代修复冲突消解算子,从而进一步提升了问题求解的优化性。
3) 建立模拟数据集并开展了实验分析论证,实验表明,负载均衡算子、任务集聚算子以及迭代修复冲突消解算子分别实现了31.50%、15.60%、70.57%的平均优化性能提升;与基于NSGA-II算法构建的NSGA-II-TTC&DT相比,论文构建的KG-NSGA-II-TTC&DT在世代距离(Generational Distance, GD)指标上实现了16.75%的平均性能提升,在最小化任务冲突时长、最大化天线负载均衡度以及最大化任务集聚度3个优化目标上分别实现了6.67%、9.28%以及1.87%的平均优化性能提升。
1 问题描述及模型建立
相较于一般的卫星地面站资源规划问题,在测控数传资源一体化场景下,其约束条件更多,需要考虑的要素也更为复杂。在本节中,首先符号化描述测控数传资源一体化场景下的卫星地面站资源规划问题所涉及的要素;然后构建约束满足模型,并给出优化目标函数、决策变量以及约束条件的数学定义。
1.1 问题要素
1) 给定规划时间段[,,Δ]。为规划起始时间;为规划结束时间;Δ为规划时间段总时长。规划要素均限定在给定规划时间段内。
2) 给定颗卫星,,…,参与规划,以表示卫星集。∀∈,≡
3) 给定个卫星地面站,,…,参与规划,以表示卫星地面站集。∀∈,≡

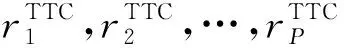

7) 给定任务集聚区间[-,+],其中表示参考时间;表示参考时间半径。
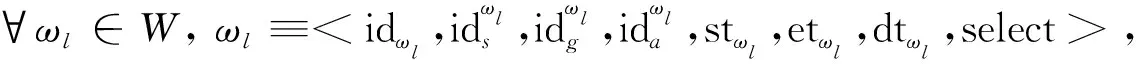
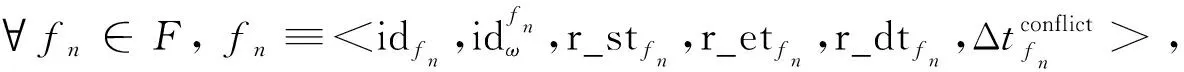
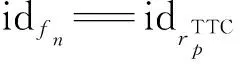
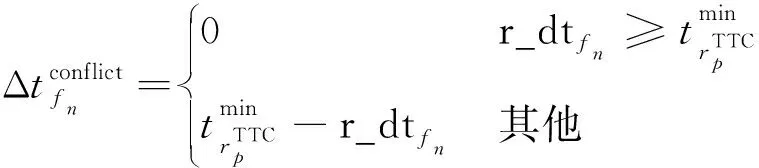
(1)
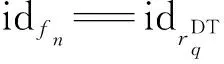
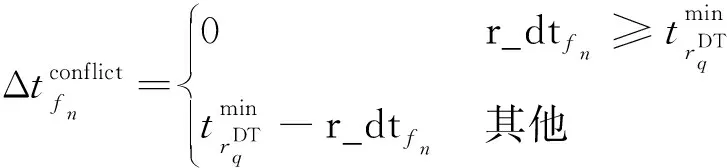
(2)
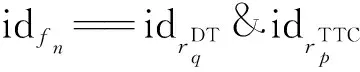
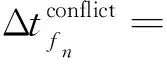
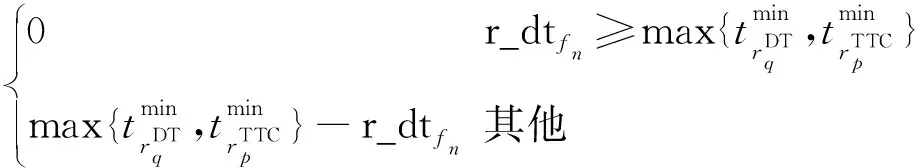
(3)
1.2 约束满足模型构建
在构建测控数传资源一体化的卫星地面站资源规划问题约束满足模型前,首先根据问题特点作假设如下:
1) 地面站天线资源能够无差别地支持参与规划的测控任务及数传任务,且具备同步执行同一卫星的测控任务与数传任务的能力,不考虑同步执行不同卫星测控任务与数传任务的情况。
2) 只考虑静态规划情况,即在规划时间段内问题要素是确定不变的。
基于以上假设建立约束满足模型,模型包括函数、决策变量以及约束条件,分别定义如下:
1) 函数
任务冲突总时长:
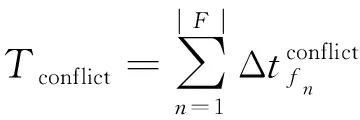
(4)
天线资源的工作时长:

(5)
式中:表示规划结果集中属于天线资源的子集。
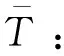
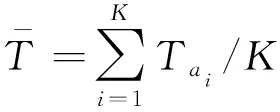
(6)
天线资源,,…,工作时长标准差:
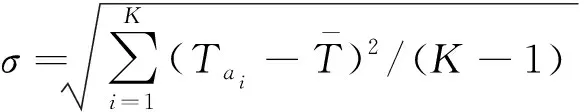
(7)
天线资源相对于任务集聚区间[-,+]的任务集聚度:
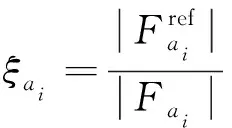
(8)
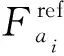
天线资源,,…,相对于任务集聚区间[-,+]的平均任务集聚度:

(9)
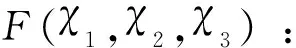

(10)
式(10)中以最小化形式表达优化目标,最小化可表达最大化天线负载均衡度,最小化(1-)可表达最大化任务集聚度。
2) 决策变量
布尔逻辑变量select:

(11)
另有r_st为时间变量,决定的起始时间;r_et为时间变量,决定的结束时间。
3) 约束条件
C1为规划要素约束。本文涉及的规划要素均限定在规划时间段[,, Δ]之内。
[-,+]⊆[,]
(12)
∀∈→[st,et]⊆[,]
(13)
∀∈→[r_st,r_et]⊆[,]
(14)
C2为天线能力约束。任意时刻,天线资源至多与某一卫星处于任务执行状态,即要求在时间轴上无重叠,表示规划结果集中属于天线资源的子集。

(15)
C3为卫星能力约束。任意时刻,卫星至多与某一天线资源处于任务执行状态,即要求在时间轴上无重叠,表示规划结果集中属于卫星的子集。
→[r_st,r_et]∩[r_st,r_et]=∅
∀,∈
(16)

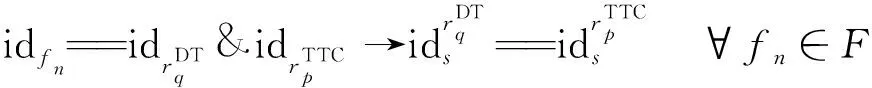
(17)
C5为任务切换约束。天线资源由任务状态切换至任务状态时必须满足执行完毕且二者的时间间隔大于的最短任务准备时长。
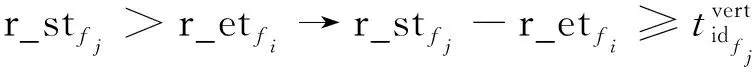
∀,∈
(18)
C6为任务执行时间约束。任意规划结果的起止时刻均限定在相应的可见时间窗口之内。
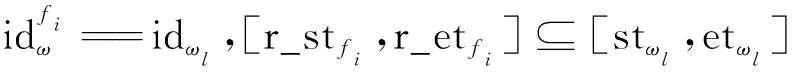
∀∈→∃∈
(19)
2 算法设计
在本节中,首先介绍测控数传资源一体化场景的卫星地面站资源规划算法KG-NSGA-II-TTC&DT的设计框架;其次详细描述算法设计框架中各部分的设计思路及其作用。
2.1 KG-NSGA-II-TTC&DT算法框架
KG-NSGA-II-TTC&DT算法设计框架如图1 所示。算法以可见时间窗口集、待规划测控任务集、待规划数传任务集以及任务集聚区间[-,+]为输入,以随机方式形成设定规模的初始种群并基于初始种群执行迭代进化操作,当迭代次数或运算时间满足设定的结束条件时,迭代进化过程结束并输出由末代种群中所有非支配解构成的帕累托前沿以及在优化目标上具有最佳折衷性能的膝解,与膝解对应的个体经解码策略处理后形成规划结果集。迭代进化过程中,以交叉、变异、个体适应度评估、膝点计算、以膝点为参考点更新种群等操作引导算法优化进程;以负载均衡算子、任务集聚算子提升个体负载均衡度以及任务集聚度的优化性能;以迭代修复冲突消解算子处理约束满足模型的约束条件,最小化任务冲突时长的优化目标也在此过程中得到优化。
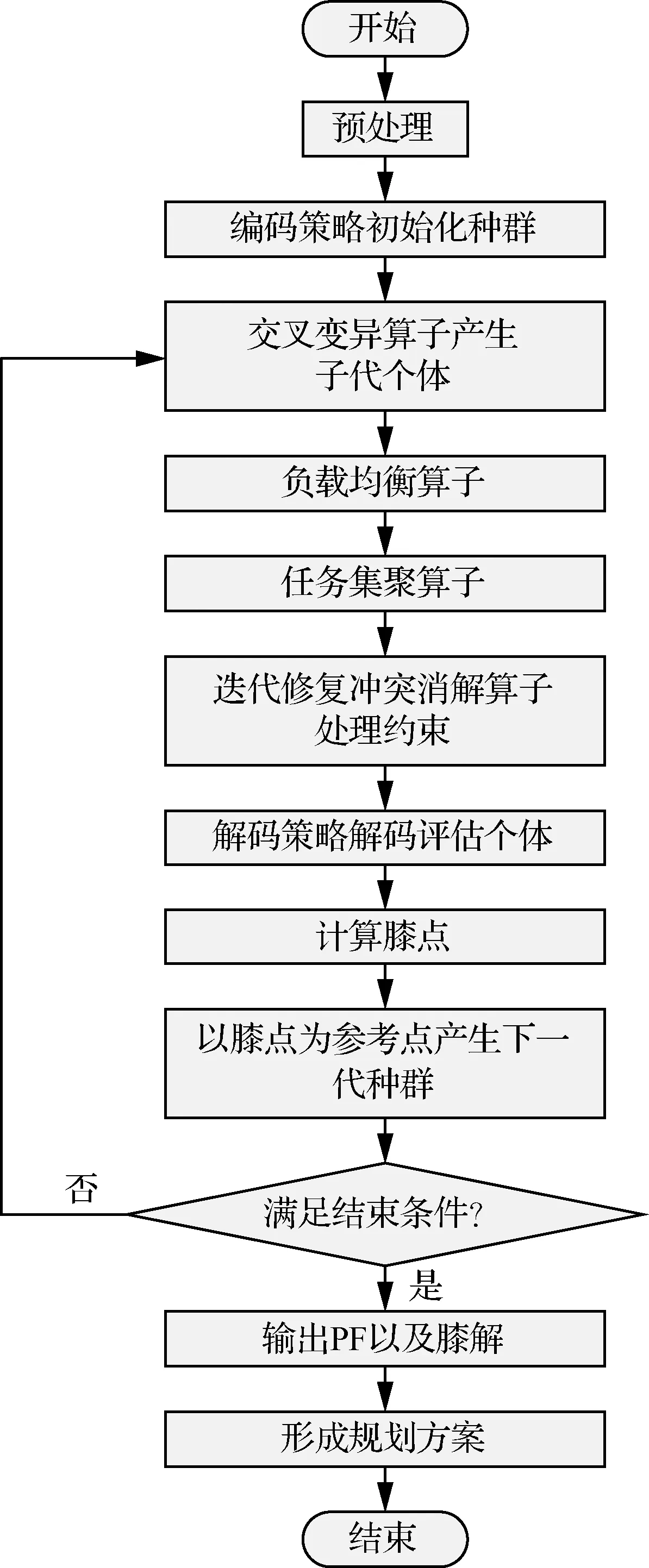
图1 KG-NSGA-II-TTC&DT算法框架Fig.1 Framework of KG-NSGA-II-TTC&DT
2.2 KG-NSGA-II-TTC&DT设计思路
2.2.1 预处理
预处理主要包括中高轨卫星可见时间窗口分割操作以及测控数传任务的匹配操作,其中高轨卫星可见时间窗口分割操作的执行对象为可见时间窗口集中属于中高轨卫星的部分,分割过程如图2所示,测控数传任务的匹配操作以待规划测控任务集以及待规划数传任务集为执行对象,匹配过程如图3所示。
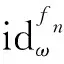

图2 中高轨卫星可见时间窗口分割示意图Fig.2 Illustration of visible time window segmentation for medium and high orbit satellites

图3 任务匹配示意图Fig.3 Illustration of task matching
在测控数传资源一体化规划场景中,天线资源具备一体化执行测控任务和数传任务的能力,但要满足约束条件C4。测控数传任务匹配操作的目的是在满足C4约束条件的前提下使得尽可能多的测控任务与数传任务一体化执行,以节约天线资源,达到事半功倍的效果。在图3中,以A、B、C等字母表示任务序列中的卫星标识符,以数传任务集为参考,针对测控任务集逐个执行卫星标识符匹配操作,将划分为匹配集与失配集,分别以黑色虚线和红色虚线指示,蓝色虚线指示占位符,以使得匹配集与数传任务集具有一致的排列次序。
2.2.2 编码策略
编码策略是以某种形式的个体编码为媒介建立待求解问题与数值序列的一一对应关系。本文以相关联的个体编码对形式建立待规划数传任务集及测控任务集与可见时间窗口集之间的数值对应关系。编码策略以待规划数传任务集以及经匹配处理后的测控任务集为输入,输出以实数形式表示的一对个体编码,称为染色体对,其中实数的数值表示执行任务id的可见时间窗口在支持任务id的可见时间窗口集中的序号,如图4所示。
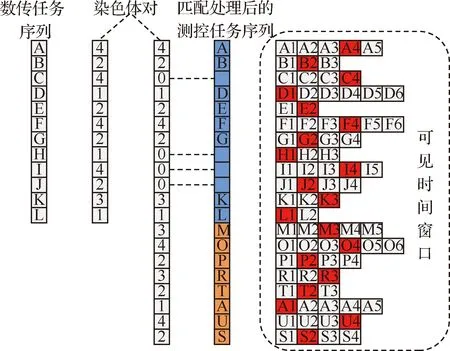
图4 编码策略Fig.4 Encoding strategy
在图4中,测控任务集经匹配处理后形成的匹配集以蓝色背景表示,失配集以橙色背景表示,执行任务的可见时间窗口以红色表示,编码规则为:数传任务集序列与匹配集序列关联编码,二者在匹配位数值一致;匹配集序列中的占位符以数值0编码;非匹配集独立编码。为了更易理解,以数传任务序列中卫星标识符为A、C的任务以及失配集中卫星标识符为T的任务为例予以说明,支持卫星标识符为A的数传任务的可见时间窗口共计5个,分别为A1、A2、A3、A4、A5,以随机方式选择其中一个(A4被选择)执行任务,A4处于第4位,故编码数值为4,匹配集序列中的匹配位关联编码为4;支持卫星标识符为C的数传任务的可见时间窗口共计4个,其中C4被随机选择执行任务,编码数值为4,匹配序列中的占位符编码为0;失配集中的卫星标识符为T的测控任务在可见时间窗口T2执行,编码数值为2。
2.2.3 交叉、变异算子
KG-NSGA-II-TTC&DT算法的每一次迭代进化过程中,父代种群在设定概率的控制下通过交叉、变异算子联合作用产生子代种群,子代种群规模与父代种群规模一致。交叉算子以二元锦标赛方式在父代种群中选择个体,在交叉概率的控制下执行交叉操作,其过程如图5所示。在图5中,交叉算子以随机方式确定交叉点1、交叉点2,通过交换父个体1、2中由交叉点1、2确定的染色体片段产生子个体。
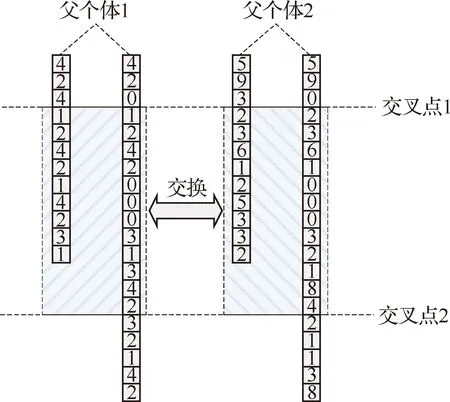
图5 交叉算子Fig.5 Crossover operator
变异算子以交叉算子输出的子个体为父个体,在变异概率的控制下执行变异操作产生下一代子个体,其过程如图6所示。在图6中,父个体即为交叉算子输出的子个体,在变异概率的控制下选择部分位置执行变异操作(以红色背景标示),当变异点位于数传任务序列对应的个体编码部分时执行联动变异;当变异点位于测控任务失配集对应的个体编码部分时执行随机变异操作,即随机更改变异点编码数值。以下重点介绍联动变异操作的过程。
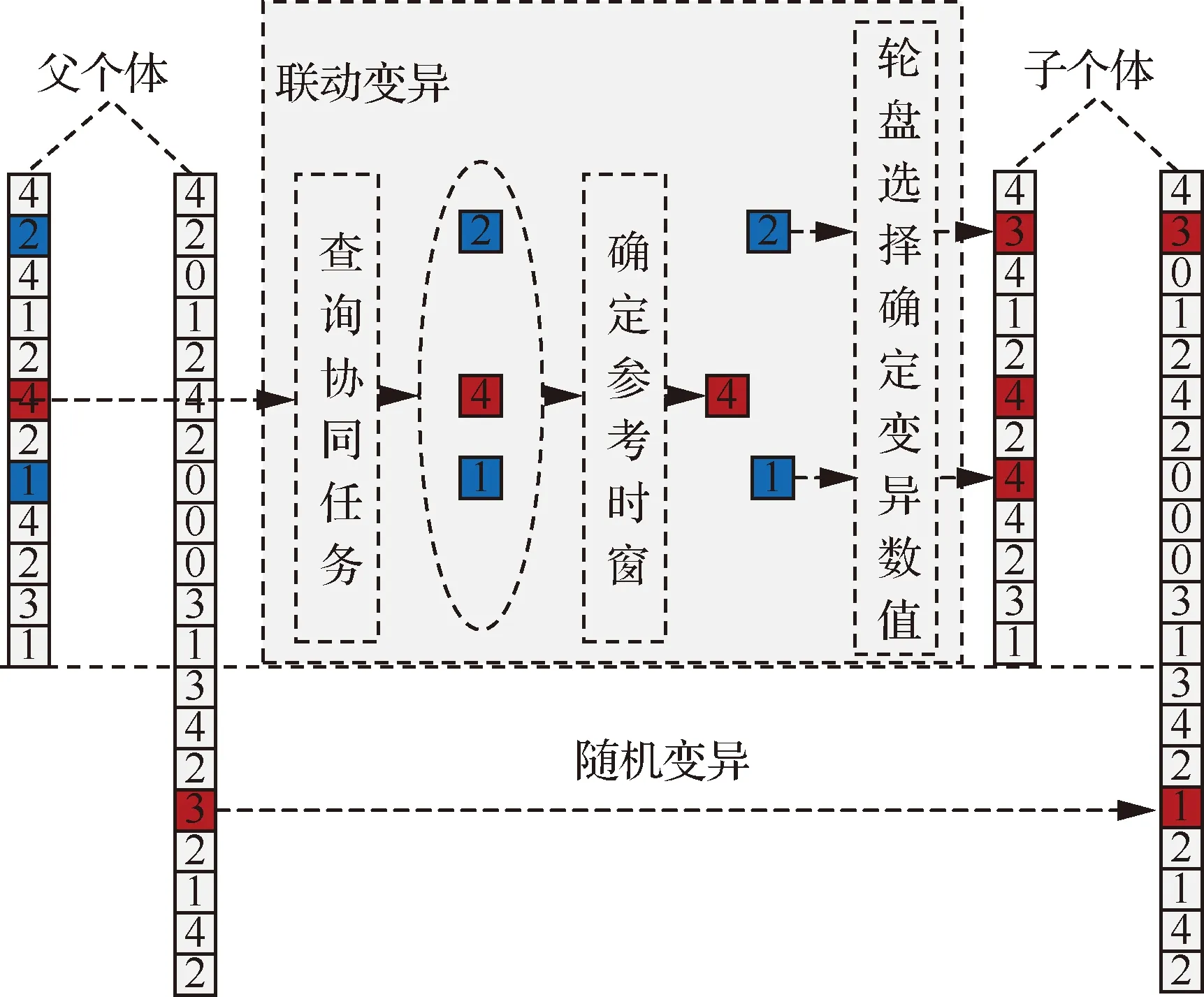
图6 变异算子Fig.6 Mutation operator
联动变异操作首先以变异点数传任务的协同标识符查询与之协同的其他数传任务;其次比较协同组(具有相同协同标识符的所有数传任务)内所有数传任务的执行时窗,以起始时刻最早的执行时窗作为参考时窗;最后以轮盘选择方式确定协同组内其他数传任务的变异数值,轮盘选择概率与距参考时窗的时间距离成反比。由上述描述可知,联动变异操作的目的在于缩减协同组内数传任务之间的时间间隔,提高协同任务执行的时效性。
2.2.4 负载均衡算子
负载均衡算子以最大化天线资源的负载均衡度为目标,通过有限次的循环操作使得参与规划的天线资源具有相对一致的工作时长,循环次数等于天线资源的数量。在每次的循环操作中均以具有最大工作时长和最小工作时长的天线资源为执行对象,平衡二者之间的工作时长,在此平衡过程中,优先将最大工作时长天线资源中距参考时间较远的任务调整至最小工作时长天线资源中距参考时间较近的位置。负载均衡算子的执行过程如图7所示。
在图7中,步骤 ① 平衡天线资源6、7的工作时长,在此过程中,优先将天线资源6中距离参考时间较远的任务调整至天线资源7,并将其安排在天线资源7中距离较近的位置,以使得由天线资源6调整而来的任务尽量在天线资源7的任务集聚区间内执行;步骤 ② 平衡天线资源3、4的工作时长,步骤 ③ 平衡天线资源2、8的工作时长,后续操作不再赘述。通过柱状图可以清晰地看出,负载均衡算子可以较好地平衡参与规划的天线资源的工作时长。
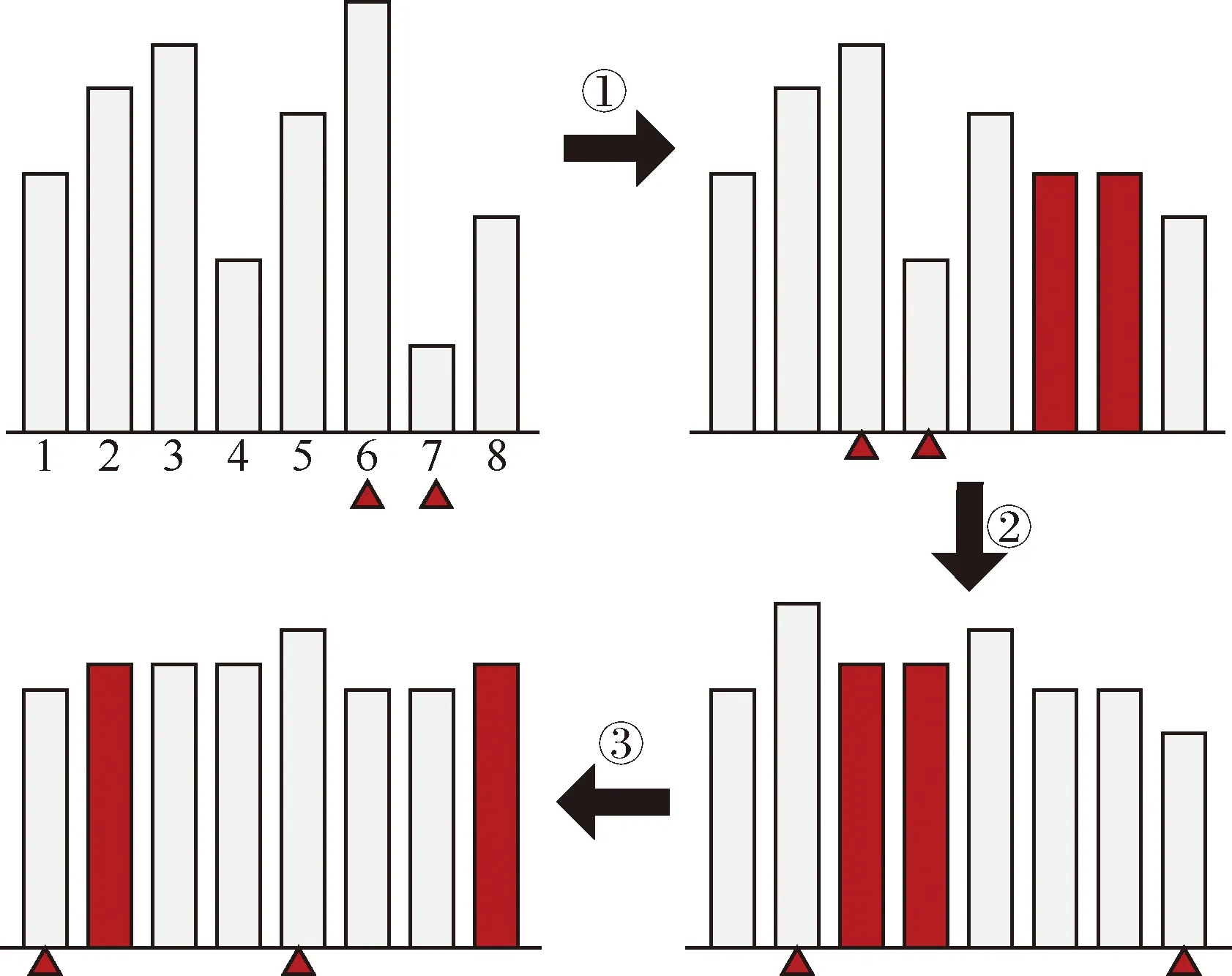
图7 负载均衡算子示意图Fig.7 Illustration of load-balance operator
2.2.5 任务集聚算子
任务集聚算子针对最大化任务集聚度的优化目标而设计,以使得任务在设定的任务集聚区间[-,+]内分布相对聚集,区间外分布相对稀疏。该算子分别作用于参与规划的每个天线资源的任务子集(任务子集由个体编码确定),将处于任务集聚区间外部的任务调整至距离参考时间最近的位置,如图8所示。
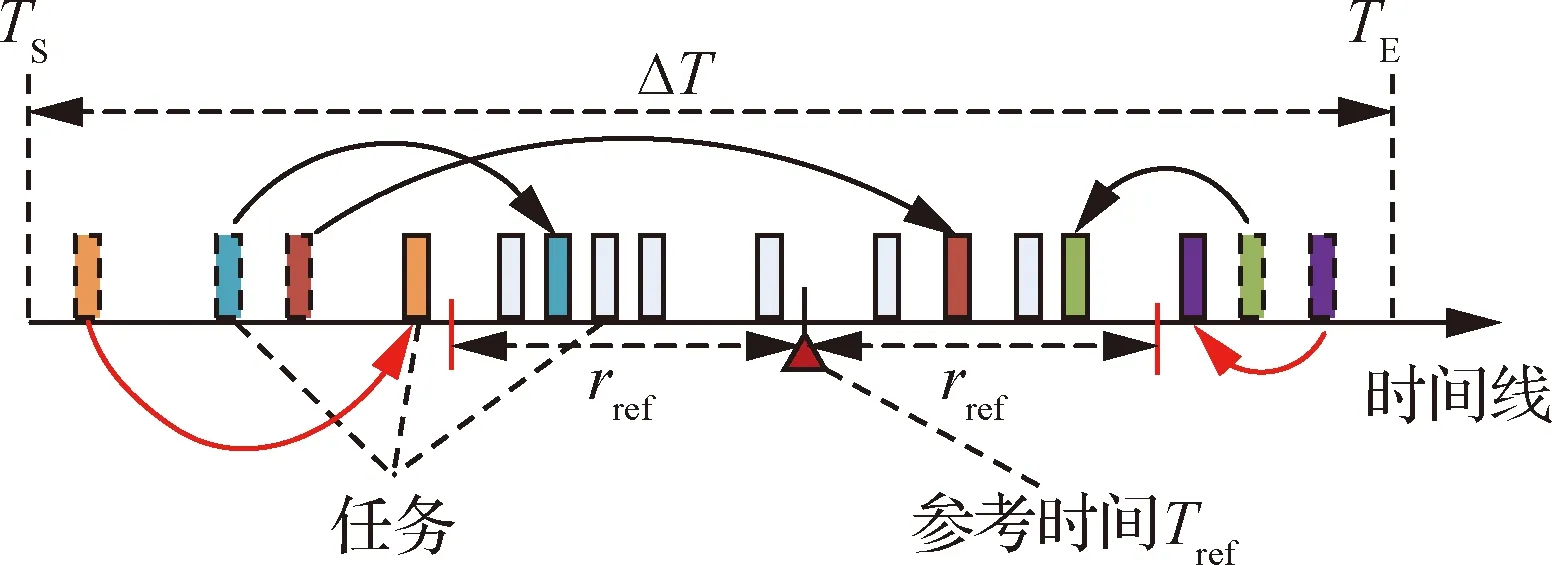
图8 任务集聚算子示意图Fig.8 Illustration oftask-clustering operator
在图8中,以柱状色块表示任务,其中虚线边框的任务均执行了调整操作,部分任务被调整至任务集聚区间内部(以黑色实箭头线指示),部分任务由于在任务集聚区间内没有支持其的可见时间窗口而被调整至区间外部距离参考时间最近的位置(以红色实箭头线指示)。
由2.2.4节可知,负载均衡算子在执行平衡操作过程中涉及天线资源之间的任务调换,且优先将距离参考时间较远的任务调整至其他天线资源中距离参考时间较近的位置,在一定程度上有利于任务集聚度的提升;而任务集聚算子只作用于参与规划的每个天线资源的任务子集,即只执行天线资源内部的任务调整操作,天线资源之间无任务调换,不影响负载均衡算子的作用效果。
2.2.6 迭代修复冲突消解算子
迭代修复冲突消解算子针对最小化任务冲突时长的优化目标而设计,并处理约束条件C2、C3、C5、C6,以确保规划结果的可行性,其执行过程如图9所示。
在图9中,迭代修复冲突消解算子首先针对个体编码确定的待执行任务序列执行冲突消解处理,并将该任务序列划分为冲突集和非冲突集;其次针对冲突集中的每个任务,以收益高低的优先级顺序,随机选择一定数量的支持该任务的可见时间窗口并计算每个可见时间窗口与非冲突集之间的冲突时长,选择具有最小冲突时长的可见时间窗口执行该任务并插入非冲突集,冲突时长的计算方式由式(1)~式(3)确定。迭代修复冲突消解算子的执行过程也是以式(15)~式(18)为准则确定决策变量r_st、r_et的过程。
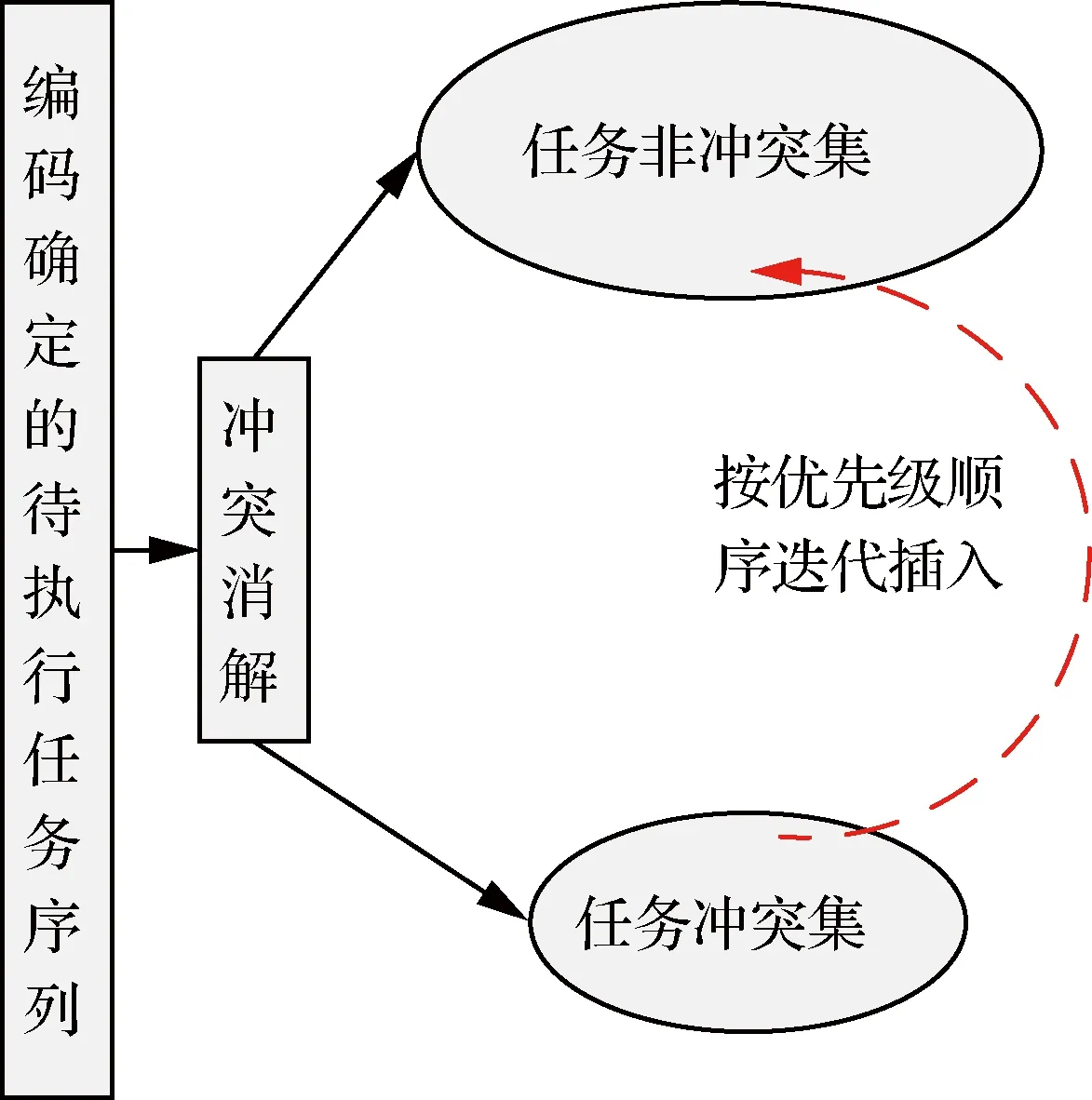
图9 迭代修复冲突消解算子示意图Fig.9 Illustration ofconflict-resolution operator based on iterative repair
2.2.7 基于切比雪夫距离的膝点定义方法
对于多目标优化问题而言,膝点指具有最佳性能折衷的解。Deb和Gupta通过对一系列回归、排序、聚类以及工程设计问题进行论证得出结论:常用的问题求解方法产生的解往往位于膝点。长期以来,由于缺乏对“最佳性能折衷”的严格定义导致膝点具有多种定义方式。Branke等基于角度(Reflex Angle)测度和基于边际效用函数(Marginal Utility Function)测度定义膝点。Das提出基于法向边界相交(Normal Boundary Intersection)的膝点定义方法。Rachmawati和Srinivasan提出基于加权和函数变换的膝点定义方法。Chiu等以帕累托前沿与理想点(Ideal Point)之间的曼哈顿距离为准则定义膝点。以上关于膝点的定义方式存在不唯一或不具备全局性的缺点。本节中,定义了一种基于切比雪夫距离的膝点,即

(20)
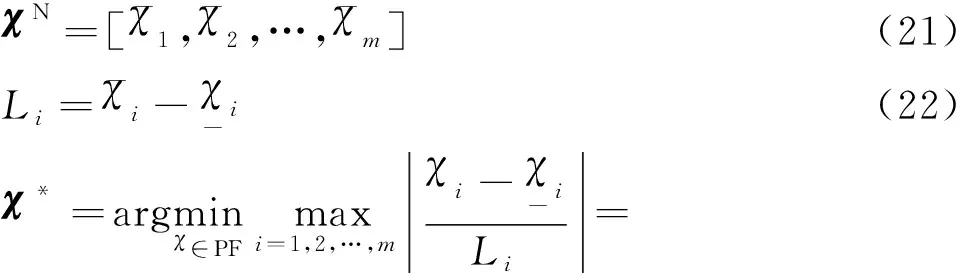
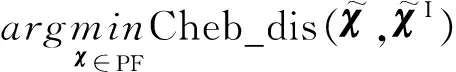
(23)

2.2.8 KG-NSGA-II-TTC&DT种群更新策略
KG-NSGA-II-TTC&DT算法基于T-NSGA-II构建,其中T-NSGA-II算法是一种基于目标区域的偏好多目标进化算法,该算法在二维及三维优化问题上性能优异,亦支持参考点的偏好表达方式。当T-NSGA-II工作在参考点模式时,其种群更新策略为:① 合并父代种群与子代种群形成合并种群;② 根据帕累托非支配排序准则对合并种群执行分层操作,按优先级顺序逐层加入下一代种群,直至临界层;③ 计算临界层个体与设定的参考点之间的切比雪夫距离并分配等级,根据切比雪夫距离等级优先级选择进入下一代种群的临界层个体,直至达到下一代种群规模。
KG-NSGA-II-TTC&DT的种群更新策略与T-NSGA-II基本一致,不同之处在于KG-NSGA-II-TTC&DT不需要设置参考点,而是以每次迭代过程中帕累托前沿的膝点为参考点引导算法进程,使得算法在膝点附近具有更好的收敛性,即KG-NSGA-II-TTC&DT引入了参考点动态更新机制。
3 实验与分析
MOEAFramework是JAVA环境下的多目标进化算法开源程序库,本文实验基于此开源程序库实现。实验平台的硬件配置:Windows 8(64位)操作系统、Intel(R) Core(TM) i5-2430M处理器、4 GB RAM。
3.1 实验设置
规划时间段设置为2020/3/5 00∶00∶00—2020/3/6 00∶00∶00,参与规划的卫星集及天线资源集均选自STK数据库,并利用STK计算可见时间窗口集,以确保约束条件C1中的式(13)和式(14)得到满足。天线资源集均位于中国境内(佳木斯、北京、青岛、渭南、喀什、厦门、南宁、三亚)。测试用例如表1所示,在表1中,以“Sat”表示卫星集的数量,涉及的中高轨卫星数量在小括号中予以表示;以“GS”表示天线资源集的数量;以“Win”表示可见时间窗口集的数量;以“DT-Task”表示待规划数传任务集的数量,其中小括号中的2项数值分别表示独立数传任务数量和协同数传任务数量;以“TTC-Task”表示待规划测控任务集的数量;以“Rev”表示任务总收益。

表1 测试用例Table 1 Scenarios for experiment
参考时间设置为2020/3/5 15∶00∶0,参考时间半径设置为32 400 s;中高轨卫星可见时间窗口分割时间间隔Δ设置为300 s;种群规模设置为100;交叉概率设置为0.9;变异概率设置为0.02。KG-NSGA-II-TTC&DT算法的结束条件通过以下方式确定:针对每个测试用例运行(+)s(其中表示优化目标数量,这里取值为3),绘制算法的收敛曲线,根据收敛曲线设置算法结束条件。图10绘制了S1~S5测试用例在指定运行时间内的收敛特性,根据收敛特征设置S1~S4测试用例的算法结束条件为50 000次个体评估次数,设置S5测试用例的算法结束条件为25 000次个体评估次数。
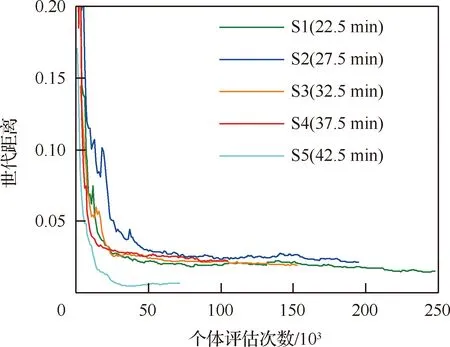
图10 KG-NSGA-II-TTC&DT算法收敛曲线Fig.10 Convergence curves of KG-NSGA-II-TTC&DT
3.2 实验分析
测控数传资源一体化场景下的卫星地面站资源规划问题无标准参考集,为了解决参考集的问题,以NSGA-II算法的种群更新策略替代KG-NSGA-II-TTC&DT算法的种群更新策略构建了NSGA-II-TTC&DT算法,针对S1~S5测试用例分别以KG-NSGA-II-TTC&DT、NSGA-II-TTC&DT算法各独立运行15次,收集帕累托非支配解形成各测试用例的近似参考集。针对S1~S5测试用例,以KG-NSGA-II-TTC&DT各独立运行30次进行实验分析。
3.2.1 负载均衡算子有效性验证
本节分析验证KG-NSGA-II-TTC&DT算法中负载均衡算子的有效性。针对测试用例S1~S5,以无负载均衡算子的KG-NSGA-II-TTC&DT算法各独立运行30次,实验结果如图11 所示。
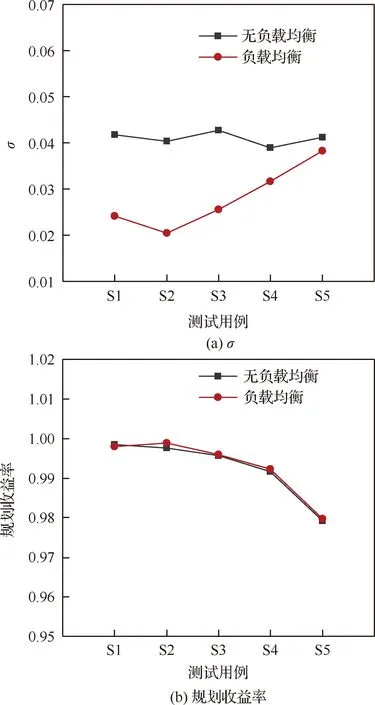
图11 负载均衡算子实验分析Fig.11 Experimental analysis of load-balance operator
在图11(a)中,纵坐标表示天线资源工作时长标准差,越小则表示天线资源的负载均衡度越大,横坐标表示测试用例,以黑色表示KG-NSGA-II-TTC&DT算法在无负载均衡算子条件下的实验结果,以红色表示含负载均衡算子时的实验结果。对比分析实验结果可知,负载均衡算子在S1~S5测试用例中均降低了天线资源工作时长标准差,有效提升了天线资源的负载均衡度;无负载均衡算子时,S1~S5在30次独立运行结果中的平均值分别为0.041 74、0.040 33、0.042 69、0.038 95、0.041 18,含负载均衡算子时,S1~S5在30次独立运行结果中的平均值分别为0.024 16、0.020 41、0.025 56、0.031 62、0.038 27,计算可知负载均衡算子在S1~S5测试用例分别实现了42.11%、49.39%、40.13%、18.82%、7.07%的性能提升,平均性能提升为31.50%。在图11(b)中分析了负载均衡算子对于规划收益率的影响,实验结果显示负载均衡算子对规划收益率的影响甚微。
3.2.2 任务集聚度算子有效性验证
本节分析验证KG-NSGA-II-TTC&DT算法中任务集聚算子的有效性。针对测试用例S1~S5,以无任务集聚算子的KG-NSGA-II-TTC&DT算法各独立运行30次,实验结果如图12 所示。
在图12(a)中,纵坐标表示优化目标(1-),其中表示平均任务集聚度,横坐标表示测试用例。对比分析实验结果可知,任务集聚算子在S1~S5测试用例中均有效提升了任务集聚度;无任务集聚算子时,S1~S5在30次独立运行结果中(1-)的平均值分别为0.044 63、0.044 10、0.079 73、0.098 67、0.135 31,含任务集聚算子时,S1-S5在30次独立运行结果中(1-)的平均值分别为0.040 98、0.038 04、0.065 00、0.078 30、0.112 35,计算可知任务集聚算子在S1~S5测试用例分别实现了8.18%、13.74%、18.47%、20.64%、16.97%的性能提升,平均性能提升为15.60%。图12(b)分析了任务集聚算子对于规划收益率的影响,实验结果显示该算子在一定程度上降低了规划收益率,在S1~S5测试用例上分别引起了0.12%、0.04%、0.20%、0.25%、0.37%收益损失,平均收益损失为0.20%,与15.60%的平均任务集聚度性能提升相比是可接受的。
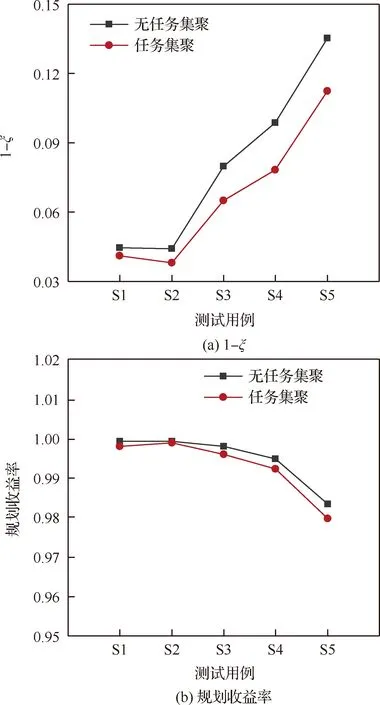
图12 任务集聚算子实验分析Fig.12 Experimental analysis of task-clustering operator
3.2.3 迭代修复冲突消解算子有效性验证
本节分析验证KG-NSGA-II-TTC&DT算法中迭代修复冲突消解算子的有效性。针对测试用例S1~S5,以无迭代修复冲突消解算子的KG-NSGA-II-TTC&DT算法各独立运行30次,实验结果如图13所示。
图13中,纵坐标表示规划收益率,横坐标表示测试用例。对比分析实验结果可知,迭代修复冲突消解算子在S1~S5测试用例中均有效提高了规划结果的收益率;无迭代修复冲突消解算子时,S1~S5在30次独立运行结果中的规划收益率平均值分别为66.92%、62.53%、57.93%、55.13%、51.01%,含迭代修复冲突消解算子时,S1~S5在30次独立运行结果中的规划收益率平均值分别为99.80%、99.88%、99.59%、99.23%、97.97%,平均收益率为99.29%,与无迭代修复冲突消解算子的运行结果相比,平均性能提升为70.57%。

图13 迭代修复冲突消解算子实验分析Fig.13 Experimental analysis of conflict-resolution operator based on iterative repair
3.2.4 KG-NSGA-II-TTC&DT性能分析
为验证KG-NSGA-II-TTC&DT算法的有效性,引入NSGA-II-TTC&DT、NSGA-II-H以及NSGA-II-MA进行对比分析。其中,NSGA-II-TTC&DT算法以NSGA-II算法的种群更新策略替代KG-NSGA-II-TTC&DT的种群更新策略,无膝点引导机制;NSGA-II-H、NSGA-II-MA算法是针对测控场景或者数传场景的卫星地面站资源规划算法,以最小化规划失败率和最大化负载均衡度为优化目标,论文加以改进使得其能够适用于测控数传资源一体化场景。针对S1-S5测试用例,分别以KG-NSGA-II-TTC&DT、NSGA-II-TTC&DT、NSGA-II-H、NSGA-II-MA各独立运行30次。

图14 KG-NSGA-II-TTC&DT实验分析Fig.14 Experimental analysis of KG-NSGA-II-TTC&DT
为了定量分析算法性能,以求得的近似参考集为参考,计算KG-NSGA-II-TTC&DT、NSGA-II-TTC&DT在S1~S5测试用例上的世代距离(Generational Distance, GD)指标,GD值越小表明算法的收敛性越好,其中GD指标的计算方法如式(24)所示,统计结果如表2所示。
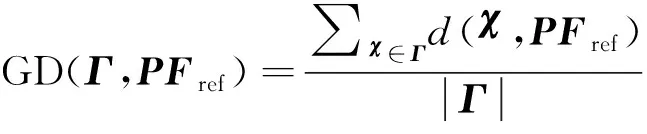
(24)
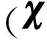
由表2可知,KG-NSGA-II-TTC&DT算法在S1~S5测试用例上的GD指标均优于NSGA-II-TTC&DT算法,分别实现了7.70%、2.12%、31.70%、26.44%、15.80%的GD性能提升,平均性能提升约16.75%,即KG-NSGA-II-TTC&DT算法具有更好的收敛性。
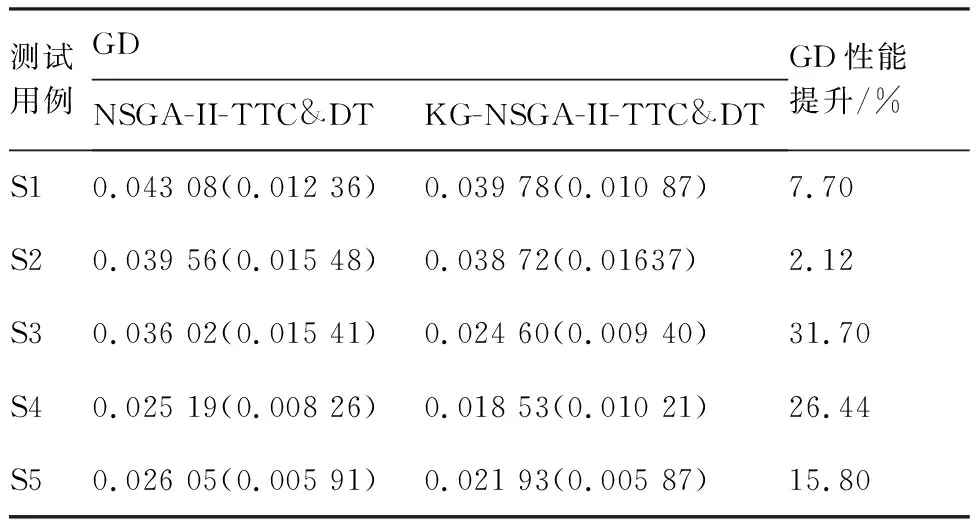
表2 GD指标性能分析Table 2 Performance analysis of GD
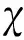
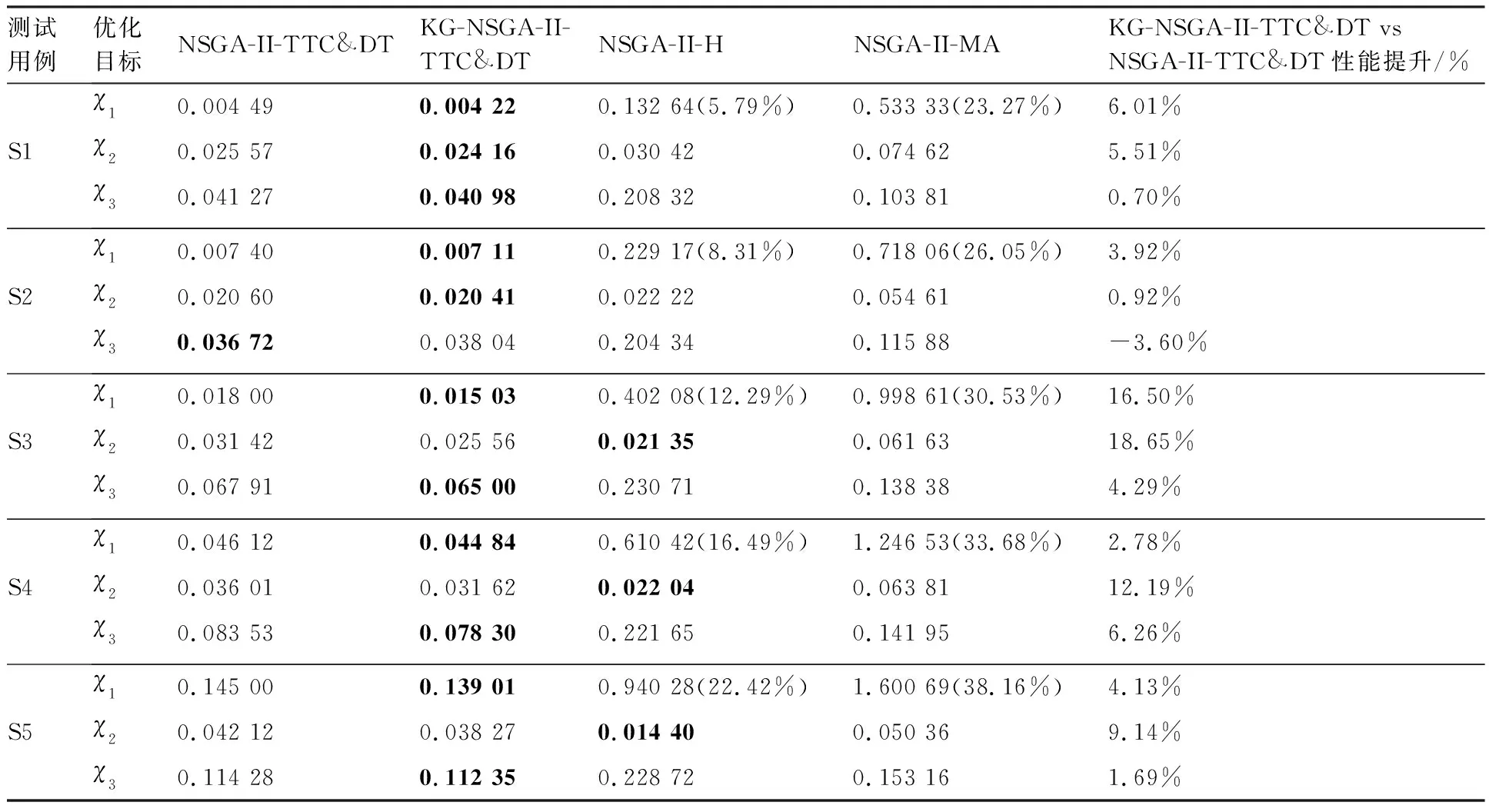
表3 优化目标数值分析Table 3 Computational analysis of optimization objectives
3.2.5 KG-NSGA-II-TTC&DT膝点规划效果
本节以测试用例S1、S5对KG-NSGA-II-TTC&DT算法的规划效果予以分析,随机选择KG-NSGA-II-TTC&DT算法在S1、S5测试用例下求得的膝点,规划效果如图15~图17所示。图15分析了S1、S5测试用例在膝点处的负载均衡情况,以JMS、BJ、QD等命名天线资源,由图可知,KG-NSGA-II-TTC&DT算法无论在任务量相对低的S1测试用例还是在任务量相对较高的S5测试用例,均实现了较好的负载均衡效果,S1、S5测试用例下天线资源工作时长最大值与最小值之间的时差分别为39.48、119.88 min。图16分析了S1、S5测试用例在膝点处的任务集聚情况,纵坐标表示任务集聚区间[-,+]外的任务占比,实验中设置的任务集聚区间外的时间段占规划时间段的25%,由图可知,S1、S5测试用例中膝点处的任务集聚区间外的任务占比显著低于25%,此外,随着任务量的增加(与S1相比,S5任务量增加了88.89%),任务集聚区外的任务占比变大,这是由于随着任务量的增加,任务集聚区内的任务冲突程度加重,导致部分任务只能规划于任务集聚区外部,图17也证实了这一点。由图17可知,S1、S5测试用例在膝点处的天线资源平均冲突时长分别为1.06、24.60 min,与S1、S5测试用例在膝点处的天线资源平均工作时长470.85、803.70 min相比,冲突时长占比分别为0.225%、3.061%。
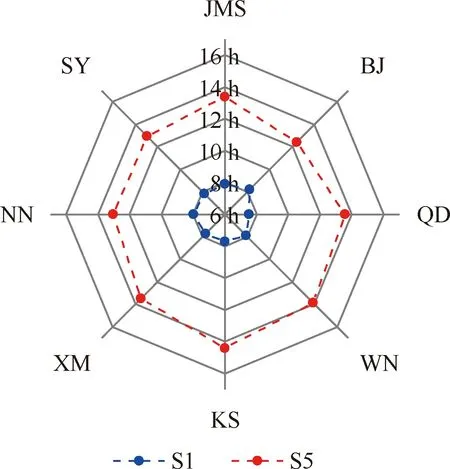
图15 膝点的负载均衡效果Fig.15 Result of load-balance in knee point
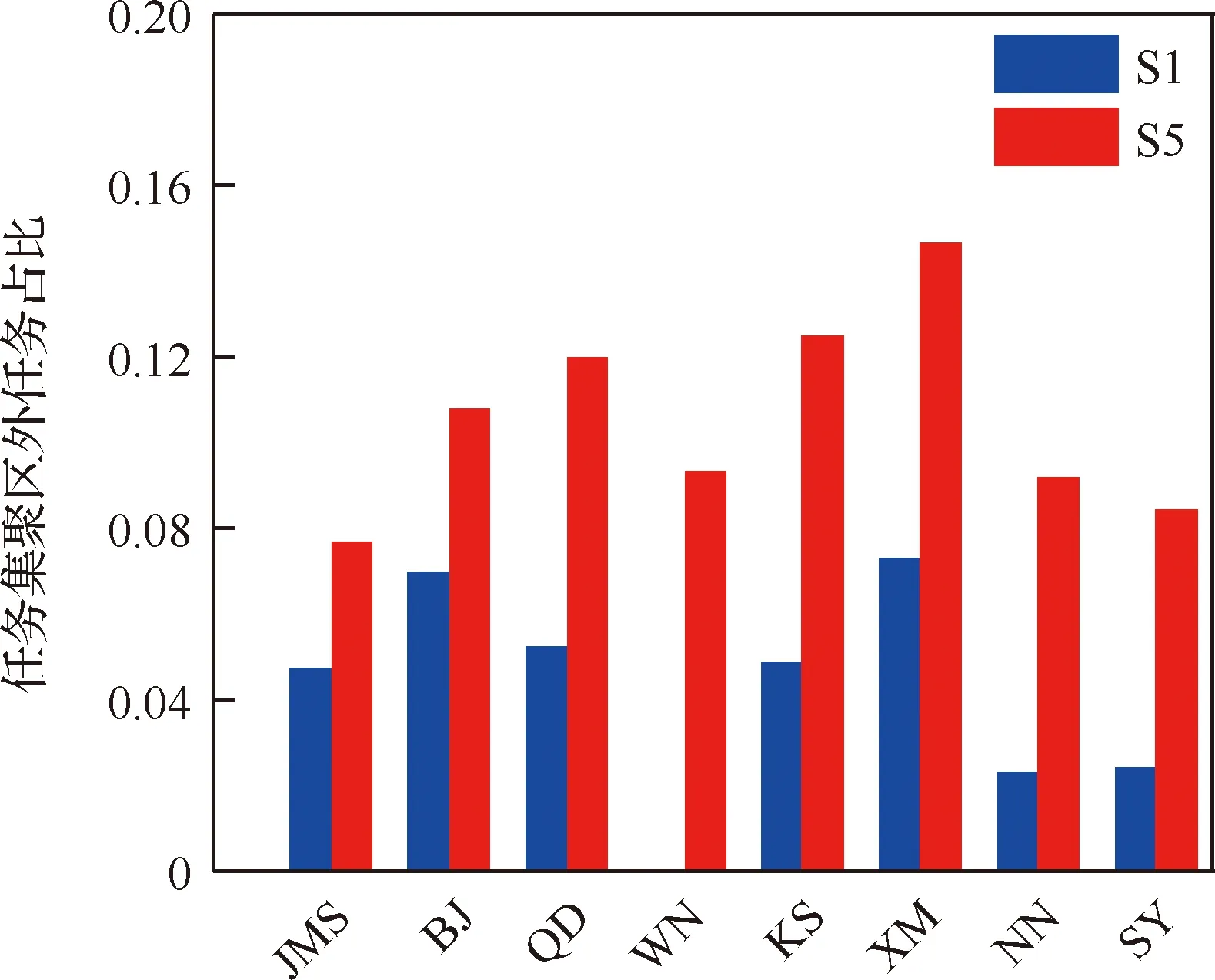
图16 膝点的任务集聚效果Fig.16 Result of tasks clustering inknee point
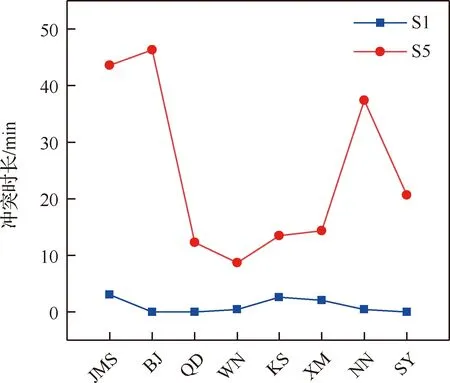
图17 膝点的冲突时长Fig.17 Conflict time in knee point
4 结 论
1) 论文针对测控数传资源一体化场景下的卫星地面站资源规划问题特征和工程实践需求,抽象建立涵盖最小化任务冲突时长、最大化天线负载均衡度以及最大化任务集聚度优化目标的约束满足模型,提出一种基于切比雪夫距离的膝点定义方法,构建了求解约束满足模型的KG-NSGA-II-TTC&DT算法,该算法以膝点为参考引导算法收敛进程,可以有效提升解的优化性。
2) KG-NSGA-II-TTC&DT算法针对优化目标设计了负载均衡算子、任务集聚算子以及迭代修复冲突消解算子以进一步提升求解的优化性。实验结果表明,负载均衡算子、任务集聚算子以及迭代修复冲突消解算子分别实现了31.50%、15.60%、70.57%的平均优化性能提升。
3) KG-NSGA-II-TTC&DT算法在膝点处具有最佳的性能折衷,可以更好满足卫星管理机构的需求,具有很强的现实针对性。
