VSV调节机构的仿真提速和精度补偿措施

张宝振, 王汉平,*,徐峰,吴志青

1. 北京理工大学 宇航学院,北京 100081 2. 中国航发商用航空发动机有限责任公司,上海 200241

可调静叶(VSV)调节机构使用可调的单级或多级叶片进行导流,可使发动机获得更大的喘振裕度,是燃气涡轮发动机预防喘振的关键机构。VSV调节机构的驱动阻滞力、理想角度调节规律与动态角度调节规律的最大偏差(简称调节精度)是VSV调节机构的重要性能指标,研究二者对不同设计参数的灵敏度,对VSV调节机构工作性能的提升具有重要指导意义。

国内外一些学者从机构运动学角度对VSV调节机构的调节规律、运动特性等问题进行了研究。文献[3-7]基于虚拟样机技术建立VSV调节机构的运动学模型,初步验证基于虚拟样机的参数化设计可用于VSV调节机构方案初期的优化分析。文献[8-9]采用机构运动学理论建立解析的VSV调节机构运动学方程,并采用智能优化算法对运动学模型的角度调节精度进行优化。此外,唐佑远和郭为忠还提出了正-逆运动学结合优化方法,有效解决了VSV调节机构的全局尺度设计优化的难题。实际状态下的VSV调节机构角度调节精度受多种因素的影响,如：关键部件的尺寸大小及其公差、装配位置偏差、非定常温度场、时变气动载荷、非线性接触摩擦、运动副间隙、部件柔性等,而采用运动学模型无法全面考虑上述因素对VSV调节机构调节精度的影响。

文献[11-13]从动力学角度分析了联动环偏心量、各级联动环支架的数目、连杆长度等参数对VSV调节机构调节精度的影响,最终结论为：摩擦和气动力是阻滞力的主要来源,且阻滞力过大会使得联动环变形严重,进而影响调节精度；装配工艺也会对阻滞力、调节精度产生影响。文献[14-15]分别基于几何精确梁理论、绝对节点坐标方法构建了综合考虑尺寸公差、运动副间隙、摇臂和联动环的柔性、部件热变形等因素的刚柔耦合动力学模型,但并未对影响机构阻滞力和调节精度的主要参数进行量化的灵敏度分析。

此外,相关研究表明：同一参数对阻滞力、调节精度的影响,有时是截然相反的,因此调整VSV机构的参数应兼顾多个性能指标。考虑接触、摩擦等非线性因素的刚柔耦合动力学模型计算规模大、计算效率低,这是制约动力学模型预测机构实际动力学特性的主要因素之一,因而在有关VSV调节机构动力学性能分析的文献中,均未定量分析和比较不同设计参数对阻滞力、调节精度的影响程度,也鲜有对改善VSV机构动力学性能进行补偿修正的公开报道。

有鉴于此,本文基于某刚性摇臂式VSV调节机构,综合考虑了影响其工作性能的关键因素,开发了参数化建模平台,并构建了VSV调节机构的五级联调刚柔耦合动力学模型；基于叶片轴与衬套之间的共形接触特性推导了轴-衬套非线性法向接触力,并仿真验证了不同接触模型对仿真精度的影响；通过简化建模单元和优化数值算法,提升了动力学模型的计算效率；在此基础上,将运动学设计研究和动力学分析相结合,采用有限差分法量化了不同参数对VSV调节机构的阻滞力、调节精度的影响程度,进而提出了降低阻滞力、提升调节精度的补偿措施,并通过数值仿真验证了补偿措施的有效性。

1 刚柔耦合动力学模型建模

1.1 机构运动原理

五级联调VSV调节机构是一种复杂空间运动机构,其运动原理如图1所示。由双液压作动筒驱动,通过活塞杆带动各级曲柄-连杆机构运动,其中：驱动联杆平动,各级曲柄与支架铰接,仅发生转动。各级联动环受同级连杆驱动而绕压气机轴线转动和沿压气机轴线平动；摇臂在联动环的带动下绕叶片轴转动；叶片上下轴分别套入机匣和静子内环的轴孔之中,随摇臂运动而沿自身轴线转动。各级叶片按照一定的联调规律进行转动,从而实现整流作用。

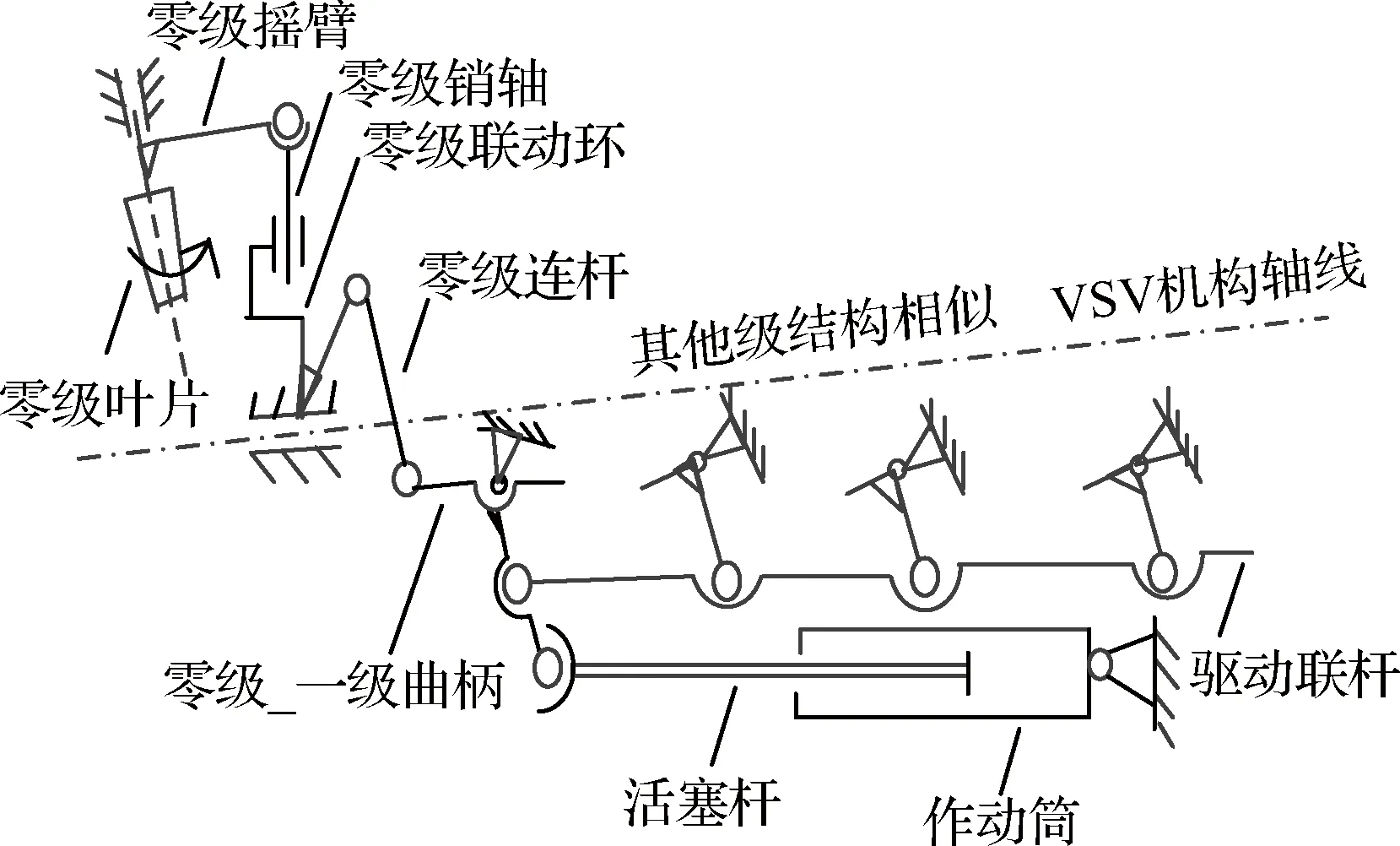
图1 VSV调节机构运动原理图Fig.1 Schematics of VSV mechanism

1.2 柔性体力学建模

Shabana提出的绝对节点坐标方法可有效解决柔性体大范围运动与弹性变形的耦合问题,比传统浮动坐标法、大转动矢量法等更能精确地描述柔性多体系统的动力学特性,同时避免了非线性的系统质量矩阵给动力学方程求解带来的困难。在VSV联调机构中,摇臂属于片长状梁结构,且联动环半径远大于其截面尺寸,因而摇臂、联动环在外力作用下均易发生变形,其变形对VSV阻滞力、调节精度具有一定影响。因此,可采用基于绝对节点坐标法的三维2节点梁单元构建摇臂、联动环的力学模型。除摇臂、联动环外,五级联调VSV刚柔耦合动力学模型中的其余部件为刚体。

刚柔耦合动力学模型采用自开发的参数化建模平台予以构建；考虑到负斜率摩擦现象,同时为避免经典库仑摩擦定律在动、静摩擦切换过程中引起的数值困难,本文采用考虑Stribeck效应的近似Coulomb摩擦模型。由于叶片轴和衬套之间存在一定的间隙,叶片轴和衬套在接触区域内存在法向和切向相对运动,且切向接触力、法向接触力与摩擦因素交互耦合在一起,因此,拟定采用力元约束近似理想几何约束以表达轴-衬套之间的接触摩擦特性,同时还能有效消除系统中可能存在的冗余约束问题。衬套扭转刚度、弹性变形以及材料因受热膨胀而产生的接触应力,可参考文献[15]的方法。

1.3 法向接触力表达

1.3.1 建立法向接触模型

对于高精度机械系统,运动副间隙较小,2部件接触区域较大, 因此这种接触问题属于共形接触,且接触刚度是接触深度的非线性函数。VSV机构中间隙运动副内的接触碰撞可视为相对碰撞速度较低的近似协调接触问题,且接触边界满足文献[20-21]中的几何刚性假设。由于叶片轴材料的弹性模量远大于非金属衬套,故假设仅非金属衬套发生变形。轴-衬套之间的接触如图2所示。

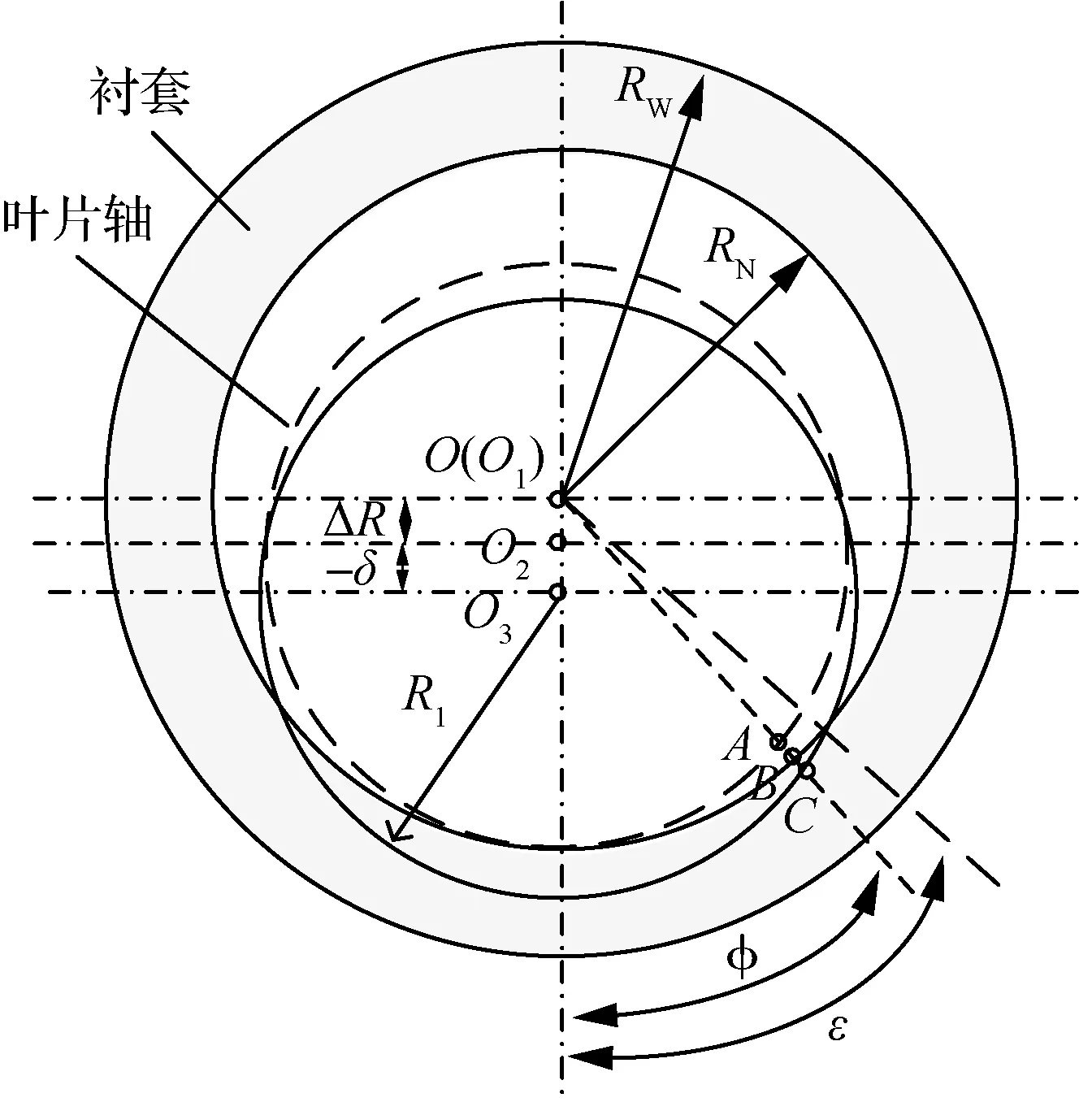
图2 轴-衬套二维接触模型Fig.2 Shaft-bushing two-dimensional contact model

在△中,由余弦定理可得：

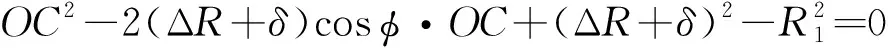
(1)

式中：轴与衬套内表面的间隙Δ=-,、为衬套内径、外径,为轴外径；为接触轮廓线上任意点对应的中心角。由于Δ≪、≪,所以Δ、的二阶及二阶以上的高次项可忽略,则轴孔接触后的接触深度为

≈(Δ+)cos-Δ

(2)

因此,接触半角近似为

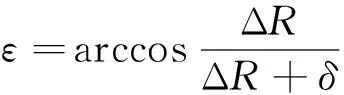
(3)

接触角度处的接触应力与衬套弹性变形之间的关系为

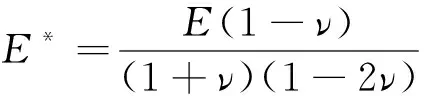
(4)

(5)

式中：、分别为衬套材料的弹性模量和泊松比;为复合弹性模量。

接触区域内产生的沿中心线的接触力为

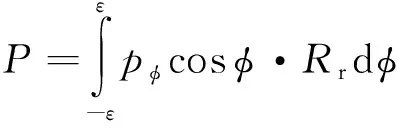
(6)

式中：为接触点与固定坐标系原点距离。由于间隙值Δ和接触深度远小于轴外径,因而≈。

对于轴向间隙相对较小的场合, 采用平面间隙模型可以满足一定的精度要求。对于长度为的衬套,三维轴-衬套接触模型的法向接触力可表示为

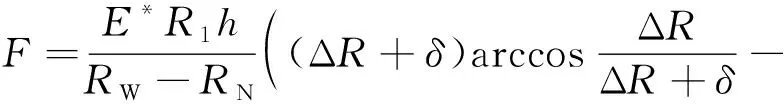
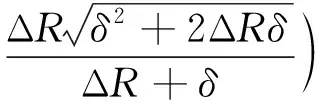
(7)

1.3.2 不同法向接触模型的差异

根据VSV机构的部件尺寸和材料属性,取叶片轴、衬套弹性模量分别为1.7×10Pa、1.5×10Pa,叶片轴外径和衬套内径均为5×10m,衬套外径、高度分别为6×10m、13×10m,轴-衬套间隙为5×10m。将侵入深度从0增大至3×10m,比较式(7)与文献[15,23-24]对应的4种轴-衬套接触模型的法向接触力,如图3所示。从图中可以看出：随着叶片轴侵入深度的逐渐增大,不同法向接触力模型计算得到的接触力差异逐渐增大。

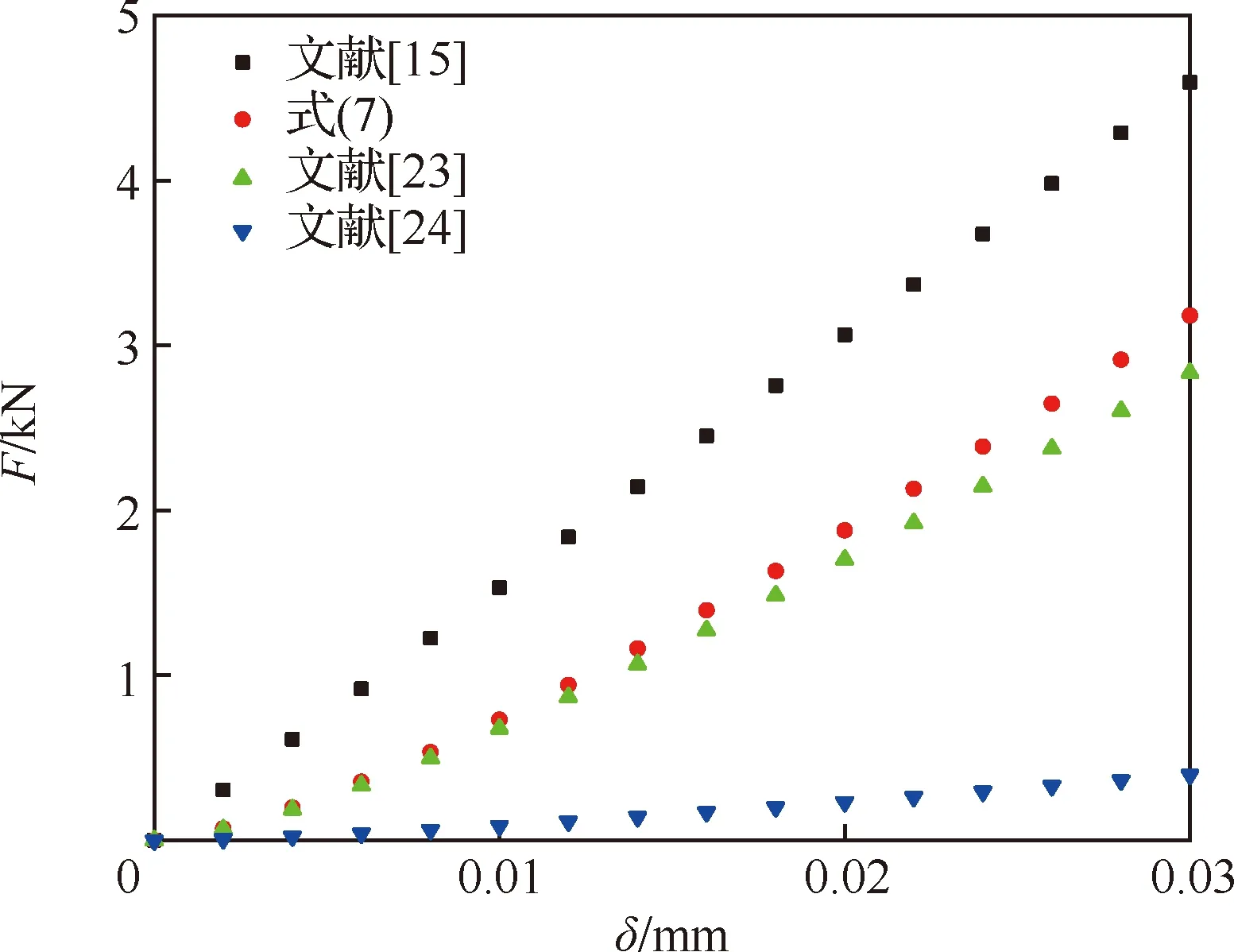
图3 不同法向接触力模型的接触力Fig.3 Contact force of different normal contact force models

1.3.3 不同接触模型对仿真精度的影响

阻滞力、调节精度是VSV机构的关键技术指标,分别定义为

=max(|()+()|2)

(8)

=max(|d()-s()|)

(9)

=max(||)

(10)

式中：为时间变量；、分别为VSV调节机构左、右作动筒的驱动阻滞力；为阻滞力均值的峰值；d(=0,1,2,3,4)为第级的叶片角度偏转的设计规律,可基于设计状态下的运动学模型仿真得到；s为基于刚柔耦合动力学模型仿真得到的第级叶片角度偏转规律；为第级角度偏差绝对值的最大值,即第级调节精度,为系统调节精度。

采用余弦位移驱动,仿真一个运动周期,仿真结果、模型计算效率如表1所示,由此可知：采用不同轴-衬套法向接触力模型进行动力学仿真,阻滞力均值和调节精度的趋势完全一致、幅值差异较小。以文献[15]模型的仿真结果为基准,阻滞力极值最大差异为0.554%,调节精度的最大差异为2.198%,而计算效率的差异则非常明显。其原因在于：VSV调节机构为低速、小间隙运动副机构,轴-衬套的法向接触力主要是限制叶片轴的方位,且作用于单个叶片的气动载荷较小,故不同接触模型对叶片轴方位不会产生颠覆性影响；于是,接触力及相应摩擦力更多只与气动载荷及驱动速度有关。

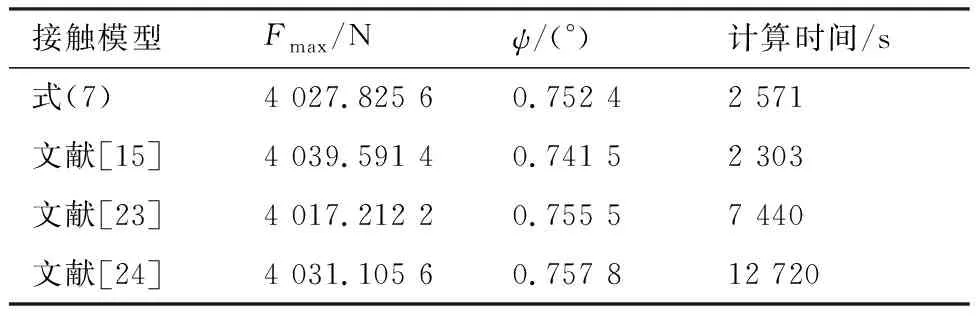
表1 采用不同法向接触力模型的仿真结果

由于采用不同法向接触力模型对应的仿真结果差异较小,因此,轴-衬套法向接触力模型可采用形式较为简单、计算效率较高的简化线性接触模型,即文献[15]中的轴-衬套法向接触模型。

2 计算效率的提升

2.1 建模单元简化

VSV调节机构中,摇臂和联动环的连接方式如图4所示。其中,销钉与联动环固连,摇臂的一端与叶片轴固连,另一端通过球轴承与销钉连接。摇臂和联动环之间存在沿VSV机构径向的相对运动,且该运动受到联动环几何边界的约束；同时,球轴承提供了摇臂和叶片轴沿摇臂旋转平面法向的旋转分量,以及2个切向的微幅转动分量。因此,基于约束等效原则,可在摇臂与联动环之间建立点在线约束,并采用单向力约束摇臂与联动环之间的相对位置关系,从而避免销轴力学模型、销轴与联动环之间约束的建模。通过这种建模单元的简化,可在极大程度上减小动力学系统的微分-代数方程组维度,从而在一定程度上降低动力学模型的计算规模。

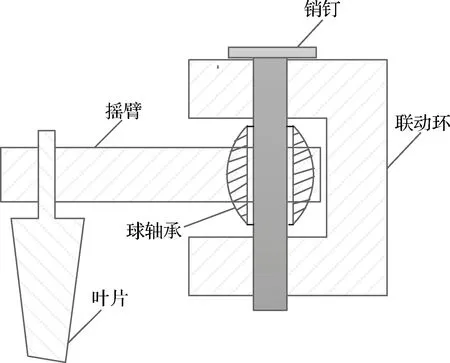
图4 摇臂-联动环的连接方式简图Fig.4 Simplified diagram of connection between rocker arm and linkage ring

2.2 力元偏导数计算

多体系统动力学方程组的求解通常转化为高维线性代数方程组,线性代数方程组的求解效率决定着微分-代数方程组的求解效率。通过子程序向系统求解器提供力元对状态变量的解析偏导数,可提高线性代数方程组的迭代效率,具体原理如图5所示。

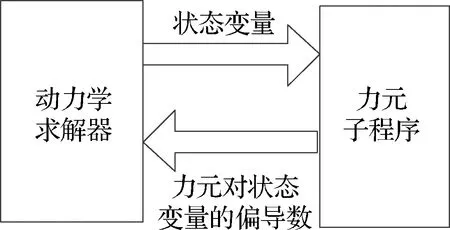
图5 求解器和子程序交互Fig.5 Interaction between solver and subroutine

基于轴-衬套之间接触力元的解析表达式,可求解各力元分量对子程序内状态变量的偏导数,并将对应的偏导数传递到系统数值积分求解器中。求解器联合力元对状态变量的偏导数、系统状态变量对广义坐标的偏导数,求解出力元对广义坐标的全微分,从而精确求出线性代数方程组迭代计算所需的雅可比矩阵。与求解器采用自动差分法计算的雅可比矩阵相比,解析的雅可比矩阵可为线性代数方程组的迭代提供更精确的方向,这在一定程度上可提升数值模型迭代求解的精度和效率。

2.3 仿真精度和计算效率验证

各参数均采用设计值,并将时变的气动载荷加载至气动载荷作用点。按照余弦位移驱动,在同一计算设备,采用同样的数值积分方法计算一个运动周期,对建模方法优化前、后的五级联调刚柔耦合动力学模型的仿真结果、计算效率进行统计,如表2所示。其中：“优化-1”对应仅采用简化建模单元方法,“优化-2”对应仅采用向求解器提供力元偏导数,“优化-1-2”对应同时采用“优化-1”和“优化-2”。从表2中可以看出：采用“优化-1”对模型计算效率提升最大,可将计算效率提升24.56%,且与优化前的刚柔耦合动力学模型计算结果相比,阻滞力最大差异仅为0.165%,调节精度最大差异仅为6.77%。因此,后续采用简化建模单元的刚柔耦合动力学模型进行参数局部灵敏度计算。

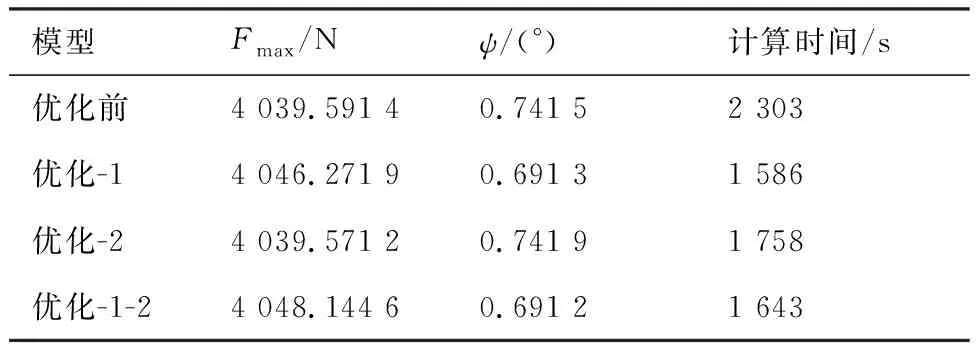
表2 计算精度和时间对比Table 2 Comparison of calculation accuracy and time

3 局部灵敏度分析

3.1 有限差分法

基于灵敏度分析可得到系统输出对输入参数的梯度,这一数值是调整模型参数、改善系统动力学响应的依据。局部灵敏度方法计算效率较高,可有效识别对目标函数影响较大的参数,因此可用于系统动力学性能补偿措施研究的初级阶段。基于优化后的刚柔耦合动力学模型,采用计算较为简便的有限差分法进行动力学局部绝对灵敏度研究。有限差分格式为

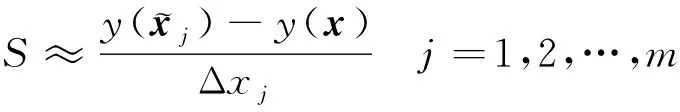
(11)

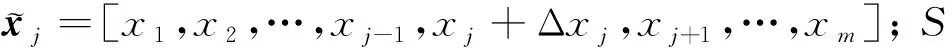
在实际系统中,影响VSV调节机构性能的往往是不同类型的物理量。因此,为综合衡量不同类型参数对VSV调节机构性能的影响程度,可采用局部相对灵敏度将局部绝对灵敏度无量纲化。局部相对灵敏度的计算公式为

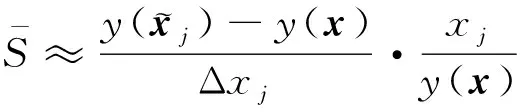
(12)

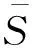
3.2 目标函数

选取式(8)和式(9)为灵敏度计算的目标函数。当各参数取运动学优化后的设计参数时,阻滞力均值随活塞杆位移变化曲线、各级叶片角度调节偏差时程曲线如图6(a)和图6(b)所示,其中,“Delta_angle_S”为第级叶片理想角度调节规律与动力学角度调节规律之差。阻滞力最大值、系统调节精度如表3所示。

由图6(a)可知：阻滞力均值随活塞杆位移变化曲线呈喇叭形,其主要原因为：活塞杆伸出行程初期,叶片处于偏开状态时,气动载荷较大,因此叶片轴与衬套之间的接触力较大,由此导致轴-衬套摩擦力、摩擦力矩较大,因而活塞杆运动初期,阻滞力较大,随后逐渐减小；活塞杆拉回行程时,阻滞力去趋势与上述趋势相反。

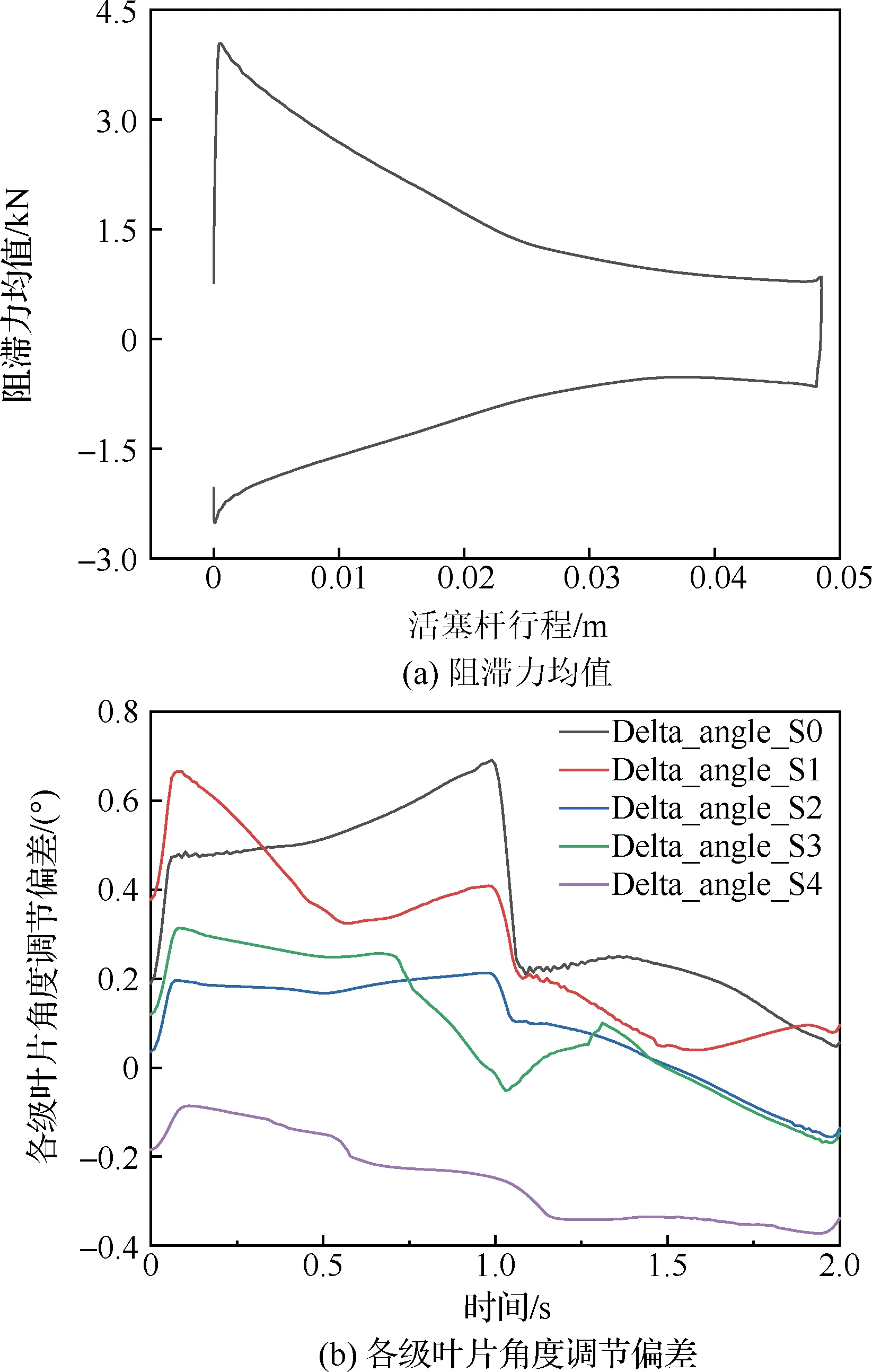
图6 参考状态下的VSV机构关键性能Fig.6 Key performance of VSV mechanism in reference state

表3 目标函数的参考值Table 3 Reference value of objective function

由图6(b)和表3可知：动力学模型中考虑气动载荷、运动副间隙、尺寸公差、温度效应、摩擦因素、部件柔性等因素综合作用时,各级叶片转角时程曲线与理想规律偏差较大,且系统最差调节精度分布在零级,也即,与设计状态相比,零级角度调节范围减小了0.691 3°。

以零级为例：在动力学仿真初始时刻,气动载荷使得周向均匀对称分布的叶片在运动副间隙范围内运动,并与柔性衬套建立接触；同时,温度效应会改变调节机构的理想驱动构型,这2方面原因使得叶片姿态偏离初始装配状态,由此导致零级叶片角度偏差曲线存在非零初值,即“初始零漂”。在活塞杆运动初始阶段,零级叶片角度偏差曲线迅速达到“局部峰值”,一方面因为在载荷和驱动的共同作用下,摇臂发生弹性变形,且叶片轴与衬套之间进一步接触；另一方面,当摇臂达到弹性变形极限,且作用于叶片轴方向的气动扭矩、摩擦阻力矩、摇臂对叶片轴的驱动力矩满足叶片轴向转动的动力学方程时,叶片方能进行稳定的角度调节,由此导致零级叶片角度调节发生迟滞。在活塞杆达到伸出行程终点时,零级角度偏差达到最大值,究其本质,乃是上述因素的综合作用使得零级角度调节范围偏小,这种情况可通过调整运动学参数对零级角度调节范围进行补偿。

零级调节精度最差,且位于活塞杆伸出行程的终点附近；一级次之,且位于机构运动初期。因此,篇幅所限,后续灵敏度分析仅列出、、对参数的灵敏度数据。

3.3 局部灵敏度

对机构进行参数调整应遵循“不大幅改变机构空间布局和部件尺寸”的原则,因此,对于VSV机构在工作状态下角度调节范围偏小这类情况,可基于运动学参数局部灵敏度分析,筛选出对角度调节范围影响较大的运动学设计参数,从而缩减灵敏度分析的参数数目。

结合筛选后的运动学设计参数、部件柔性、装配误差、润滑状态等因素进行动力学局部灵敏度分析,考察不同类型因素对VSV机构动力学响应的影响程度。具体流程如图7所示。

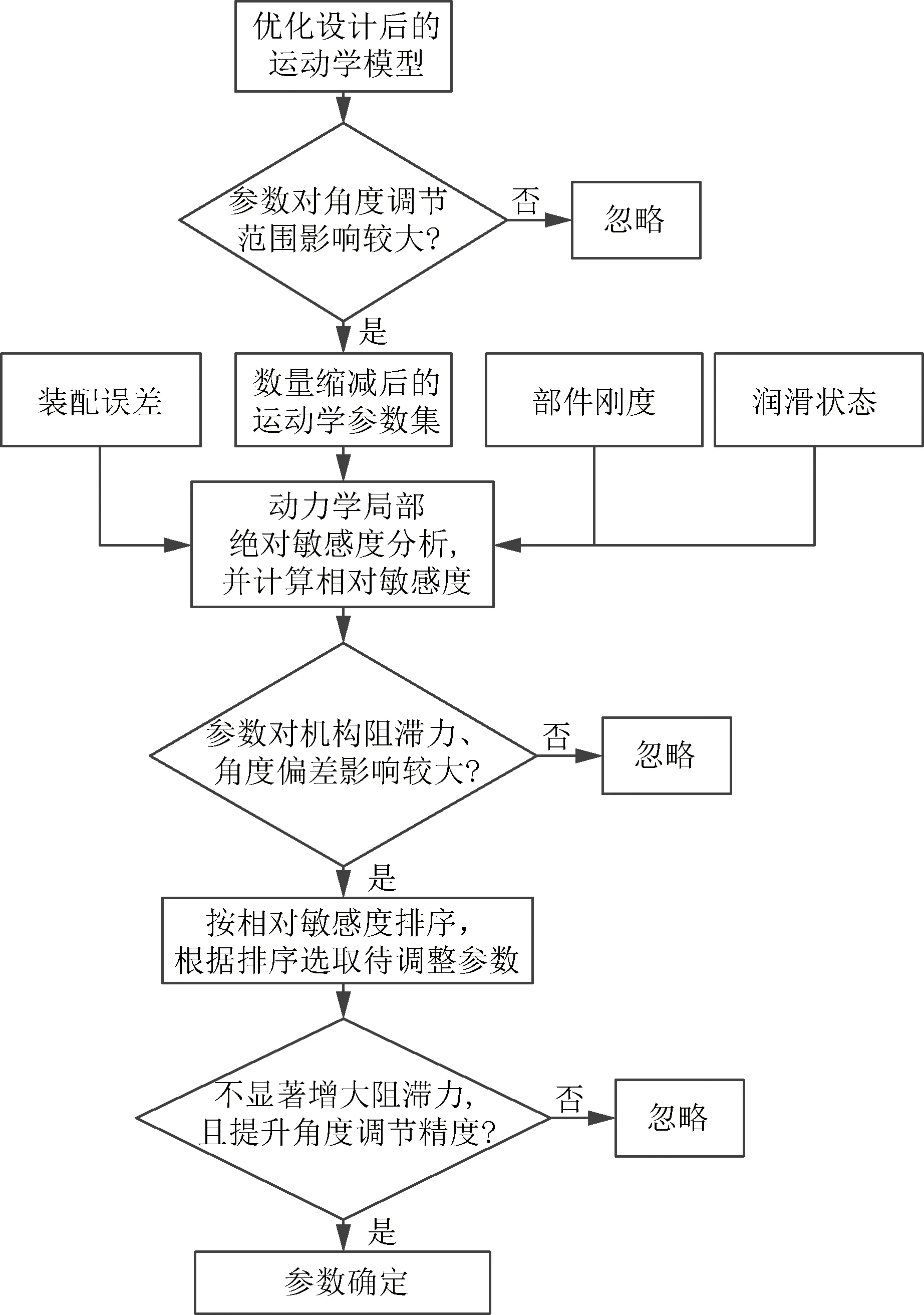
图7 局部灵敏度分析流程图Fig.7 Flow chart of local sensitivity analysis

对五级联调VSV机构进行运动学灵敏度分析,可得对角度调节范围影响较大的运动学设计参数：摇臂长度(=0,1,…,4,表示VSV机构的级数)、联动环支耳高度、曲柄长度c同时,机构调节精度还受到叶片安装角,摇臂刚度ra、联动环刚度ring、联动环安装偏心、轴-衬套摩擦系数的影响。

3.3.1 运动学设计参数

表4为目标函数对各级摇臂长度、联动huan的相对局部敏感度,由此可知：摇臂长度增大使得驱动叶片的等效力臂增大,因而导致阻滞力的减小；曲柄长度、支耳高度对阻滞力影响均较小。摇臂长度、支耳高度、曲柄长度均对同级角度调节精度有显著影响,而对其他级影响较小。

以零级摇臂为例,由运动学分析可知：零级摇臂、零级曲柄长度对零级叶片角度调节范围影响较大；当曲柄按照设计状态运动时,零级联动环半径、联动环做螺旋运动的转动角度幅值、零级摇臂长度、叶片做绕自身轴线转动角度幅值之间的关系满足：

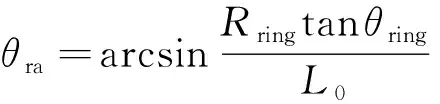
(13)

而基于动力学分析可知：零级和一级连杆由同一曲柄进行驱动,当减小零级摇臂长度时,虽然可增大零级叶片角度调节范围,但在零级和一级气动载荷综合作用下,零级叶片“初始零漂”增大,进而导致零级最差调节精度出现在“局部峰值”；而当零级摇臂长度增加时,叶片角度调节范围减小,同时使得摇臂刚度减小,由此导致零级叶片角度调节范围减小,零级最差调节精度分布在活塞杆伸出行程终点。因而,改变摇臂长度均使得零级调节精度变差。

零级支耳高度减小可增大零级叶片转角调节范围,可对因运动副间隙、温度效应、气动载荷、摩擦等因素导致的叶片转角范围偏小进行补偿,从而提升零级调节精度。

与零级摇臂相比,零级曲柄长度对零级调节精度的影响程度更大,且均使得零级调节精度变差,原因在于：虽然表4中对曲柄长度仅取4%的摄动量,但增大零级曲柄长度使得角度调节范围大幅增大,减小零级曲柄长度使得角度调节范围大幅减小,因而零级最差调节精度均分布在活塞杆伸出行程终点。其中,局部绝对灵敏度、局部相对灵敏度按照式(11)和式(12)计算。

表4 目标函数对运动学参数的局部相对灵敏度值

3.3.2 柔性部件刚度

通过改变摇臂、联动环横截面的高度来调整这2类柔性部件的刚度特性。表5为目标函数对摇臂、联动环刚度的局部相对敏感度,从中可看出：改变各级摇臂、联动环刚度对阻滞力的影响较小,且无一致的规律。原因在于：一方面,摇臂、联动环刚度增大导致柔性部件质量增大,从而使得作用于联动环上的重力、惯性载荷增大,驱动系统做功有增大的趋势；另一方面,摇臂、联动环刚度增大导致其弹性变形减小,驱动系统做功有减小的趋势。因此,改变各级摇臂、联动环刚度对阻滞力的影响取决于多因素的综合作用。摇臂、联动环刚度对同级叶片调节精度有较大影响,且刚度的增大使柔性部件的弹性变形减小、角度迟滞减小,因而调节精度增高。与零级相比,一级摇臂、联动环刚度对同级调节精度影响较大,这主要与该级叶片在偏开状态下的气动载荷较大有关。

表5 目标函数对刚度的局部相对灵敏度值

3.3.3 装配参数

图8(a)和图8(b)分别为联动环正常装配、联动环装配过程中存在右侧偏心的示意图。图中：为机匣凸台上表面沿机构径向的半径;为定位销与机匣凸台上表面的间距;为定位销与联动环固接点对应的径向半径；当联动环存在右侧偏心时,联动环对称轴线与机匣对称轴线相距Δ。第(=3,4,5,6)个定位销与对应的机匣凸台表面间距的减小量、第(=1,2,7,8)个定位销与对应的机匣凸台间距的增大量为：

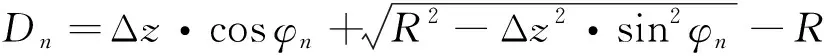
(14)

式中：为第个定位销与机构全局坐标系轴负向的夹角。

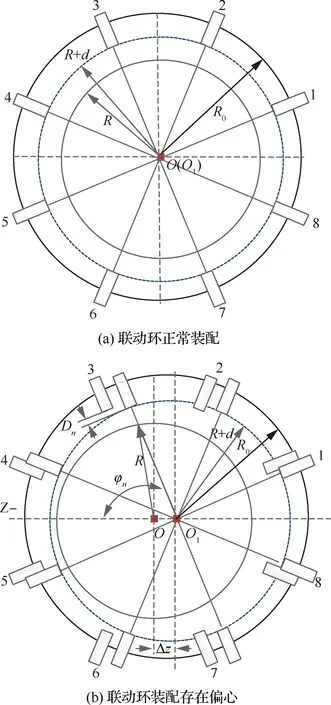
图8 联动环装配位置Fig.8 Assembly position of linkage ring

表6为目标函数对联动环偏心的局部相对灵敏度,由此可看出：联动环装配位置存在偏心对阻滞力、角度调节精度的影响程度较小。原因在于：当定位销装配到预定位置时,联动环的装配偏心量最大仅为0.1 mm,这对机构的驱动构型影响非常小。

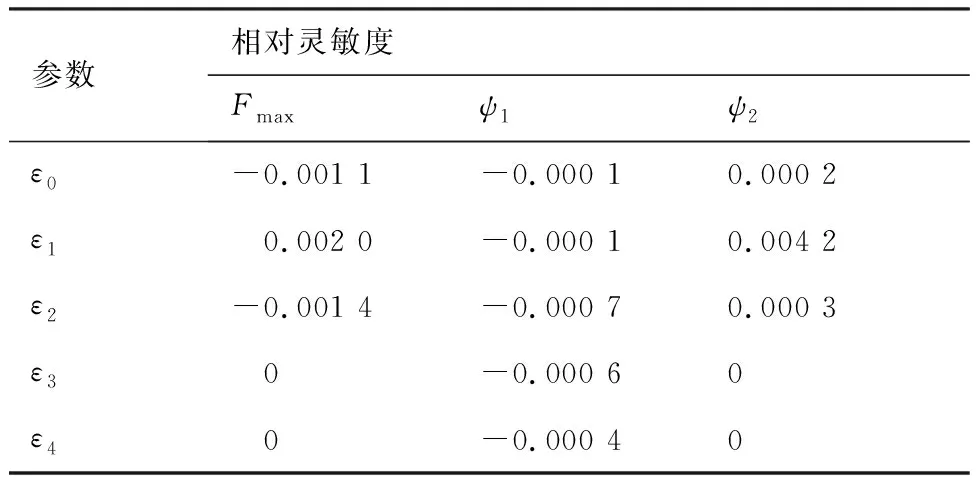
表6 目标函数对联动环偏心的局部相对灵敏度值

表7为目标函数对各级叶片安装角的局部相对敏感度,由此可看出：改变各级叶片安装角,对阻滞力影响均较小,原因在于：摇臂长度较短,且摇臂与叶片轴固连,改变叶片安装角并不会显著改变驱动叶片绕自身轴向转动的驱动力臂。

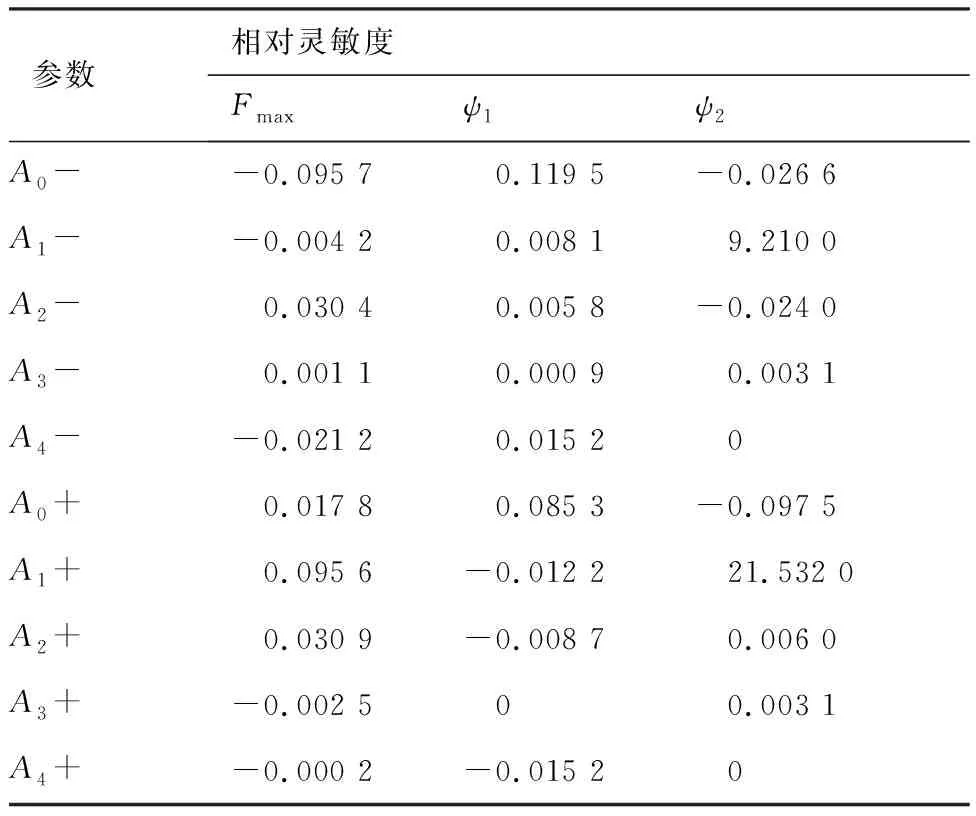
表7 目标函数对安装角的局部相对灵敏度值

减小零级、一级初始装配角,可减小由气动载荷、运动副间隙导致的“初始零漂”,从而有助于提升同级调节精度,而对其他级调节精度影响很小；与零级叶片装配角相比,一级叶片装配角对同级调节精度的影响较大,原因在于：零级叶片和一级叶片由同一曲柄进行驱动,且一级气动载荷较大,因而零级调节精度不仅受到同级参数的影响,还受到一级气动载荷的影响。

3.3.4 摩擦因素

表8为目标函数对摩擦系数的局部相对灵敏度,由此可以看出：摩擦系数对阻滞力、零级与一级的调节精度均有显著影响,且随着摩擦系数减小,阻滞力减小、调节精度增高。主要原因为：当摩擦系数减小时,各级叶片轴与衬套之间由于气动载荷、衬套弹性产生的摩擦力、摩擦力矩随之减小,因而阻滞力减小；同时,摩擦系数减小,会使得各级调节角度的滞回量减小,因而各级角度调节精度增高。

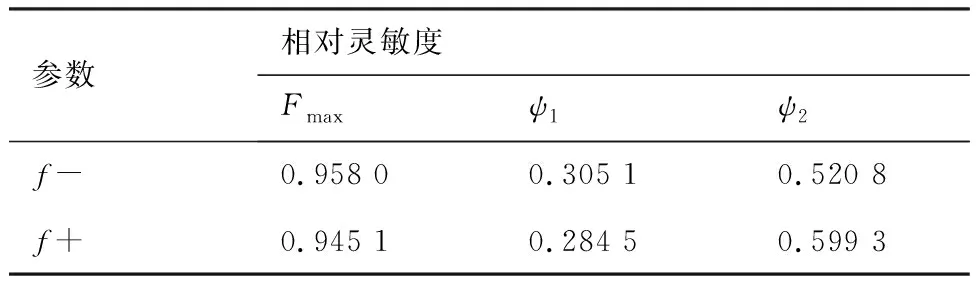
表8 目标函数对摩擦系数的局部相对灵敏度值

3.4 局部相对灵敏度分析和补偿措施

3.4.1 局部相对灵敏度

由相对灵敏度数据可知：运动学设计参数、联动环安装偏心、柔性部件刚度对阻滞力影响均相对较小；摩擦系数对阻滞力影响较为显著。

支耳高度、曲柄长度、叶片安装角、摩擦系数对调节精度影响较大,而摇臂刚度、联动环刚度对调节精度影响相对较小。

3.4.2 补偿措施

根据阻滞力、调节精度对参数的局部相对灵敏度分析结果,以“不大幅改变机构空间布局和结构尺寸、不过度增加机构质量和阻滞力,同时提升调节精度”为目标,可提出以下改善机构性能的补偿措施：

“角度调节范围”补偿。降低各级支耳高度和增大各级曲柄臂长,均可提升同级叶片转角调节范围。以调节支耳高度为例,由于系统最差调节精度发生在零级,因此可将零级支耳高度降低2 mm,以此补偿零级叶片转角调节范围的减小,进而提升调节精度。

“初始零漂”补偿。各级叶片角度的“初始零漂”是气动载荷、运动副间隙综合作用的结果,调整叶片初始安装角可对“初始零漂”进行补偿。考虑到二、三级角度偏差曲线初始值较小,且零级叶片安装角对零级调节精度影响较小,因此保持零、二、三级叶片安装角不变。为减小气动载荷、运动副间隙导致的一级叶片角度“初始零漂”,可将一级叶片安装角减小0.2°；

同理,可将四级叶片安装角增大0.2°以补偿四级叶片角度的“初始零漂”。

“响应迟滞”补偿。角度偏差曲线“局部峰值”本质是由叶片转动“响应迟滞”引起的。因此,可保持各级摇臂长度、联动环半径不变,将零级摇臂、联动环厚度各增大10%以提升刚度,减小叶片角度调节的“响应迟滞”,从而降低零级角度偏差曲线的“局部峰值”；同时,将摩擦系数减小0.02,一方面可减小各级叶片角度调节的“响应迟滞”,另一方面可大幅降低阻滞力峰值。

4 补偿措施的仿真验证

上述局部灵敏度分析方法,每次均只分析单因素改变对目标函数的影响,而多因素协同作用对阻滞力、角度偏差的影响尚不明晰；对角度偏差产生主要影响的因素较少,因此可进阶式地对VSV调节机构的调节精度进行补偿,即“采取因素渐次累积的方式补偿调节精度”。根据补偿措施,进行动力学模型参数的调整,仿真得到阻滞力曲线和各级角度调节偏差如图9所示,阻滞力峰值、系统调节精度如表9所示。

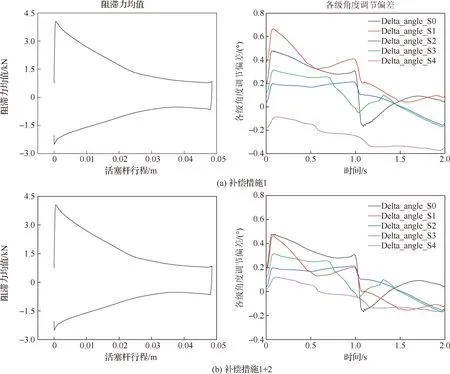
从图9以及表9可看出：所提出的补偿措施是有效的,即采取上述补偿措施,可使系统调节精度提升为0.449 4°,即调节精度提升约30%；同时,当减小摩擦系数时,阻滞力大幅降低。

表9 补偿措施验证Table 9 Verification of compensation measures

5 结 论

解析推导了考虑运动副间隙的轴-衬套法向非线性接触力模型,基于参数化建模平台,构建了考虑关键部件尺寸误差、接触摩擦、运动副间隙、温度效应、部件柔性等因素的五级联调VSV调节机构刚柔耦合动力学模型。通过简化建模单元、解析表达力元偏导数的方法提升了刚柔耦合动力学模型的计算效率,采用有限差分法分析了阻滞力峰值、各级调节精度对参数的动力学局部灵敏度,并据此提出了补偿措施。基于仿真结果和分析得出如下结论：

1) 不同的轴-衬套法向接触力模型对刚柔耦合动力学模型计算效率的影响非常大,但仿真得到的阻滞力均值和调节精度的趋势、幅值吻合很好。以线性接触模型为基准,阻滞力均值最大差异为0.554%,调节精度的最大差异为2.198%,因此,对于低速、小间隙运动副的VSV调节机构,可采用计算效率较高的线性接触模型近似表达轴-衬套的法向接触特性。

2) 简化建模单元、提供力元对状态变量的解析偏导数,均可提升动力学模型计算效率。当基于约束等效原则对建模单元进行简化时,可在仿真阻滞力最大差异为0.165%,调节精度最大差异为6.77%的情况下,将刚柔耦合动力学模型的计算效率提升24.56%。

3) 基于运动学设计和动力学仿真的综合分析,减少了动力学局部灵敏度分析的计算量；利用动力学局部相对灵敏度分析结果甄别了不同参数对目标函数的影响程度,并结合各级叶片转角偏差曲线的归因分析,提出了有利于VSV调节机构动力学性能提升的补偿措施,仿真验证表明：采取补偿措施后,调节精度提升约30%；改善机构润滑条件可大幅降低阻滞力峰值。