基于“数据关系”的教学案例分析

江苏苏州市相城区春申中学（215143）张晓燕

信息技术课程在培养学生高阶思维方面有着独特的优势。信息技术的逐渐发展成熟，为运用信息技术促进高阶思维发展奠定了坚实的基础。本文结合三个教学案例，基于“数据关系”设计、实施教学，为学生搭建思维阶梯，培养学生的高阶思维。

一、教学现状与分析

场景一：在教学苏科版七年级“相对引用”时，教师结合课本第44 页的学生体测标准分计算汇总表，在Excel中先用单元格地址引用的方法计算J13单元格的标准分，然后将指针指向这个单元格的右下角，再向下拖动“填充柄”，这样其他单元格就会自动显示出相应的结果。看完教师的演示，学生惊叹“填充柄”这个工具的神奇。教师告诉学生，利用“填充柄”填充数据时，只是复制了其中的运算关系，对单元格的地址做了自动调整，这就是单元格地址的“相对引用”。

场景二：在教学苏科版七年级“数据图表及其分析”时，教师让学生根据课本第54 页的“选择因素分析”工作表中的数据分别绘制一个柱形图和一个饼图。学生随便选择工作表中的数据，迅速绘制出柱形图和饼图，完成教师布置的任务。

场景三：在教学苏科版八年级Python 课程内容“求圆面积”时，教师将课本中的代码“r=int（input（））；s=3.14*r**2；print（s）”在电脑中录入、运行、保存，让学生通过键盘输入一个半径值进行测试。测试成功的学生意味着完成了教师布置的任务。

上述教学场景反映出的共性问题是：教师侧重操作技能的教授，没有关注“数据关系”，不注重对学生高阶思维的培养。这样教学的结果往往是学生掌握了软件的操作和使用方法，但对操作原理知之甚少，既无法促进学生的发展，又降低了教学的有效性。

二、“数据关系”分析

“数据关系”一般指数据的因果关系和相对关系，譬如在Excel相对引用中，公式单元格与引用单元格数据之间的相对位置保持不变。而在Excel图表中，数据一般呈现5 种相对关系，即成分相对关系、项目相对关系、时间序列相对关系、频率分布相对关系和相关性相对关系，每一种相对关系都对应相应的图表。在成分相对关系里，我们的兴趣主要在各个部分所占的百分比，如男生人数占学校总人数的65%；主要关键词有份额、总数百分比、所占百分比。在项目相对关系里，我们主要想比较不同事物的排列方法，看看它们是差不多，还是一个比另一个更多或更少，如小李的英语成绩在几个同学中排名第一；主要关键词有大于、小于、高于、低于、差不多。在时间序列相对关系里，我们对“它”怎么随着时间变化感兴趣：“它”每星期、每月、每季度和每年的变化趋势是增长的、减少的、上下波动的还是基本保持不变的，如随着年级的增长，视力正常的学生的人数在不断减少；主要关键词有变化、增长、下降、增加、减少、波动、不变。频率分布相对关系主要指各数值区域内有多少项目，如初中男生的身高大多集中在1.6 米到1.7 米之间；主要关键词有x到y的范围、密度、频率、分布。相关性相对关系主要强调两个变量的关系是否符合所要证明的模式，如一般来讲，体重随着身高的增长而增加；关键词有与……有关、随……增长、随……减退、根据……变化等。

三、案例分析

在梳理案例的过程中，笔者发现了一大批与前述场景相对应且能够体现基于“数据关系”的教学案例。本文主要选择“相对引用”“数据图表及其分析”“求圆面积”三个案例来进行分析。

［案例1］相对引用

“相对引用”这节课的主要教学目标是让学生理解“相对引用”的概念。本案例主要是让学生理解公式单元格和引用单元格数据之间的相对位置关系。

从图1 可以看出，与C2 单元格相连的有8 个单元格，分别是上（C1）、下（C3）、左（B2）、右（D2）、左上（B1）、右上（D1）、左下（B3）、右下（D3）。教师在C2 单元格中输入公式“=A1”，也就是C2 公式单元格引用A1单元格的数据1，按下回车键，这时C2单元格将会显示数据1。那么C2 单元格下方的C3 单元格会显示什么呢？因为C3 单元格在C2 单元格的下方，且C2 单元格引用了A1 单元格，所以我们要寻找A1单元格下方A2单元格的数据，C3单元格的数据是2，因为它们相对位置是不变的。因此，C1 单元格的数据为A1 单元格上方的数据，而又因为A1 单元格上方没有单元格，所以会出现一个说明引用了无效单元格的符号“#REF!”。接下来，教师可以让学生说出与C2单元格相连的其他单元格的数据，并说出理由。最后，教师用“填充柄”自动填充数据，并结合讨论结果进行验证。这一教学设计让学生在操作前通过一系列的高阶思维活动，寻找数据关系，使学生真正了解了什么是相对引用以及在相对引用中为什么会出现“#REF!”这种特殊提示。

图1 单元格位置关系图

［案例2］数据图表及其分析

“数据图表及其分析”一课的主要教学目标是让学生了解各种图表适合表达什么样的数据关系。

数据图表设计步骤：首先确定所想表达的主题，接着判断其属于哪种相对关系，最后选择相对应的图表。总体思路见图2。

图2 图表设计总体思路

图表选择思维导图：能否选择合适图表的关键在于明确想要表达的具体信息，图表信息应包含成分相对关系、项目相对关系、时间序列相对关系、频率分布相对关系及相关性相对关系5 种相对关系中的一种或几种。每一种相对关系都会引导出5种相对的图表形式（见图3）。

图3 图表选择思维导图

以“选择饮料的关键因素”表格为例，这张表中笔者关注的是“183”这个数据，笔者想表达的主题是“味道因素选择人数最多”。“味道因素选择人数最多”属于项目相对关系，项目相对关系对应的是条形图（如图4）。

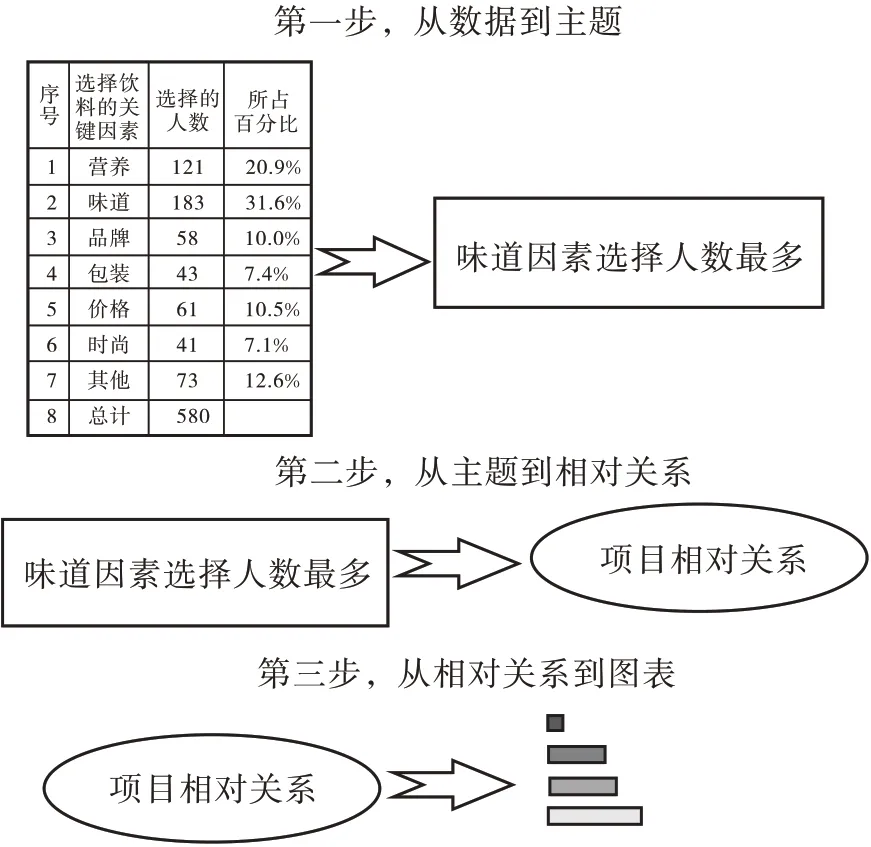
图4 “味道因素选择人数最多”图表制作过程

以上是图表设计的总体思路，在图表的实际制作过程中还应注意以下细节：对于饼形图，不宜多于6 种成分，若多于6 种，则应选择最重要的6 种，并将未选中的成分列为“其他”；人眼习惯于沿顺时针方向观察物体，因此最重要的部分可紧靠“12时”，用强烈的颜色对比突出显示；如果没有哪一部分比较重要，则可从大到小进行排列并以同种颜色显示。对于条形图，要让条形之间的距离比条形的宽度小；使用能形成强烈对比的颜色及阴影来强调重要的项目，以此来突出信息的标题。对于柱形图和折线图，如果图表中有少数几个点，就用柱形图，反之则用折线图；柱形图强调的是数量的级别，更适合反映一小段时间内发生的事件，而折线图强调角度的运动及图像的变换，能展示数据的发展趋势；尽量使柱形之间的距离小于柱形的宽度。

［案例3］求圆面积

“求圆面积”的主要教学目标是让学生编一个程序，从键盘输入圆的半径，利用圆面积公式计算并输出圆的面积。

教师在讲解程序的编写时缺少问题分析这一环节，导致学生只是模仿操作，思维没有得到锻炼和提升。教师可引导学生回顾旧知，建立新旧知识之间的联系。例如，学生在初一时学过冯·诺依曼计算机的体系结构，知道计算机由输入设备、输出设备、存储器、运算器和控制器五大部分组成。用冯·诺依曼计算机的工作原理来解析“求圆面积”程序设计的三大组成部分，发现它们实际上是一一对应的关系。程序语句r=int（input（））对应从键盘上输入一个整数，然后赋值给变量r，是程序的输入及存储部分；程序语句s=3.14*r**2 对应CPU 处理数据及存储数据，赋值给变量s，是程序的处理和存储部分；程序语句print（s）对应显示器输出结果，是程序的输出部分。教师帮助学生建立这样的一一对应关系，不仅帮助学生复习巩固了旧知识，而且加深了学生对新知识的理解，同时让学生对整个程序的设计流程有一个总体的把握。

在计算机的硬件和程序之间建立联系之后，教师可基于“数据”概念挖掘输入数据的类型。学生头脑中的“数据”可能是日常生活中的数字，而计算机中的“数据”则是信息的表现形式和载体，比如学生信息表中包括姓名、性别、年龄、照片等内容，这些都叫数据。数据有的是描述事物大小、次序的数值，有的是描述事物各方面特性的文本字符串，有的是描述事物时间属性的日期时间。教师引导学生分析半径r的输入数据类型，也就是对程序的“计算部分”进行明确，因为计算机程序只能解决计算问题，不能解决非计算问题，因此分析并理解问题的计算部分是利用计算机解决问题的前提。对问题计算部分的不同理解会产生不同的求解方法，也会产生不同功能和复杂程度的程序。理解问题的计算部分需要结合当代计算机发展水平和实际技术能力。随着信息技术的发展，人机交互方式发生了巨大的改变，从最初的键盘鼠标到触屏再到语音识别和图像识别。教师在讲解从键盘输入半径数据时，可以引导学生采用其他方式，如语音识别和图像识别输入半径数据。目前这些技术都已经成熟，语音识别可以调用科大讯飞和百度的接口，图像识别可以利用OCR 技术。利用OCR 技术进行图像识别时，若计算机中已安装有tesseract 模块，还需另外安装pytesseract 及PIL 两个模块。通过“求圆面积”的学习，学生明白了数据可以实现实时监测和爬取。

语音识别、图像识别以及实时监测和爬取对入门者来说比较困难，教师应引导学生进行理解以及变换思维。教师可以提问学生：有没有更好的输入半径的方式，使其达到自动化产生半径的效果？这其实就是用计算思维来解决问题。求圆面积时可以调用一个随机数函数来实现数据的自动输入和处理。求圆面积时随机产生一个半径数据虽然意义不大，但能使学生产生随机数的思维非常重要，这也充分体现了计算机处理程序的自动化思维。教材在之后的“体验Python”猜数游戏程序中就用到了随机数。如果我们在求圆面积时给学生渗透计算机产生随机数的思维并运用程序来实现，这对后续猜数游戏程序的编写将起到很大的促进作用，教师在教学时可将重点放在控制流上。控制流是由控制器产生的，控制流不仅可以按顺序执行，还可以通过条件语句来执行。整个程序设计其实可以归纳为三大部分（输入、处理和输出）和三种流程（顺序、分支、循环）。

通过思维变换，学生对程序设计有了大致的把握，能学会用计算思维解决问题，达到一种自动化和人性化的体验效果。

总之，操作未动，思路先行，教师只有充分认知、正确引导，为学生搭建必要的、专业的学习支架，实施合理的现场教学，才能高效实现教学目标。