等边三角形“手拉手”模型构造及解题策略研究
2022-10-10广西南宁市第十四中学530000
广西南宁市第十四中学(530000)陈 杏
等边三角形“手拉手”模型是指由两个共顶点的等边三角形构成的基本图形,其在相对位置变化的同时,始终存在一对全等三角形。如果把小等边三角形的一边看作“小手”,大等边三角形的一边看作“大手”,这样就类似“大手拉着小手”,所以称这个模型为“手拉手”模型,此模型经常在几何综合题中出现。构造等边三角形“手拉手”模型常与平行、旋转、截长补短等辅助线作法相结合。
一、从教材母题抽象出模型,厘清模型问题本质
很多考试题目的母题都来源于教材,从教材习题提取模型、类比模型和模型变式都是考试命题的方向。三角形全等证明是初中数学教学的重点内容之一,其难点在于要求学生从复杂的图形中抽象出全等三角形。
[例1](人教版八年级上册第83页第12题)如图1,△ABD,△AEC都是等边三角形,求证BE=DC。

图1
学生大多能准确地判断出本题是利用三角形全等证边等的问题,但不一定能马上给出解题思路。笔者提示学生将共顶点的等边三角形(如图2)抽取出来,学生很快就发现它们形成“手拉手”模型,并找到一对全等三角形,从而得出证明。在面对多个等边三角形时,教师可以引导学生寻找解决问题的模型——“手拉手”模型,使学生更好地理解和应用几何模型思想,提高解题效率和正确率。

图2
二、作平行线构造等边三角形“手拉手”模型
有时两个等边三角形不共顶点,这时可以通过作辅助线,构造共顶点的等边三角形,从而得到“手拉手”模型。
[例2]在等边三角形ABC中,E是边AC上一定点,D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF。
(1)如图3,若点D在边BC上,求证:CE+CF=CD。
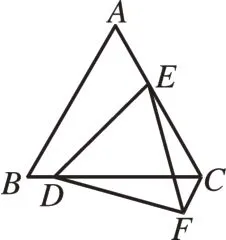
图3
(2)如图4,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系,并说明理由。

图4
虽然有教材母题的经验,但学生发现本题没有全等三角形,也找不到“手拉手”模型。对此,笔者引导学生添加辅助线。学生尝试作平行线,有学生过点E作BC边的平行线,虽然构造出共顶点的两个等边三角形,但和题目要证明的结论联系不大。笔者引导学生过点D作AB边的平行线DM,发现不但可以得到第三个等边三角形,而且其与其中一个等边三角形共顶点,“手拉手”模型出现(如图5),证明△DME≌△ECF,将CF转换为EM,即可得出证明。学生有了经验,很快可以在图4 中作平行线,构造“手拉手”模型(如图6),从而得出证明。在等边三角形中,作一边的平行线构造新的等边三角形是常用的辅助线作法,找准过哪个点作平行线,即找到了模型,可使问题迎刃而解。
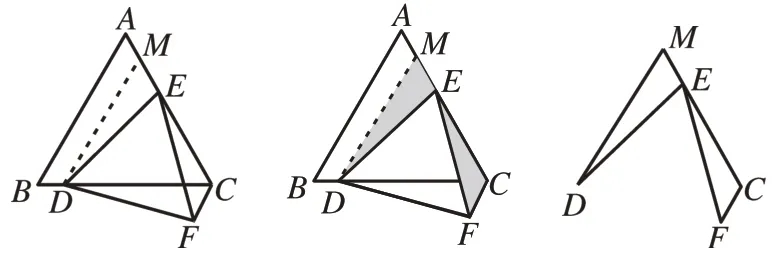
图5
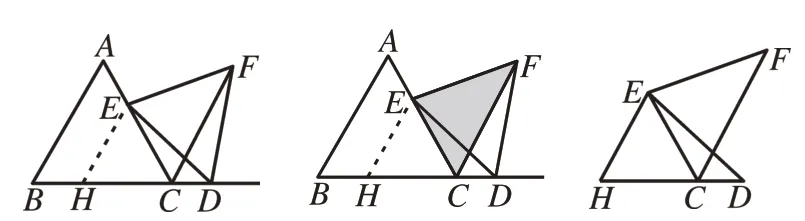
图6
三、旋转构造等边三角形“手拉手”模型
旋转也是构造等边三角形“手拉手”模型的重要途径。在旋转变换中,要注意可以旋转的前提条件,即有边相等旋转即重合,旋转特殊度数后有特殊三角形产生。有时还要注意证明旋转后点的共线。
[例3]如图7,等边△ABC中,P为△ABC外一点,连接AP、BP、CP,∠APB=∠BPC=60°,求证:AP+PC=BP。
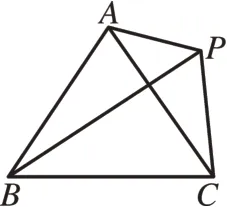
图7
对于线段和差的证明问题,通常把不在一条直线上的两条线段放在一条直线上,因此,可以将△APC绕点A顺时针旋转60°(如图8),AC与AB重合,但点P是否在BP上需要证明。利用旋转后∠AP′B=120°,AP=AP′,旋转角∠PAP′=60°,因此△AP′P是等边三角形,所以∠AP′P=60°,得到∠AP′B+∠AP′P=120°+60°=180°,从而得到B、P′、P三点共线,由此,就构造了共顶点的等边三角形△AP′P和等边三角形△ABC形成的“手拉手”模型。
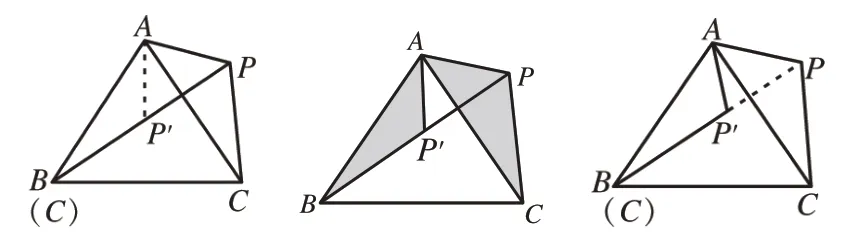
图8
四、截长补短构造等边三角形“手拉手”模型
截长补短是证明三角形全等的重要辅助线作法,对构造等边三角形“手拉手”模型也同样好用。
[例4]如图9,在等腰△ABC中,120° <∠BAC<180°,AB=AC,AD⊥BC,且交BC于点D,以AC为边作等边△ACE,直线BE交直线AD于点F,连接FC交AE于点M。(1)求∠AFC的度数;(2)探究FE,FA,FC之间的数量关系,并证明你的结论。

图9
由(1)可解得∠AFC=60°,这是构造等边三角形的有利条件,笔者鼓励学生在长线段FC上截取FG=FA,从而得到等边三角形△AFG与等边三角形△AEC构成了共顶点的“手拉手”模型(如图10)。
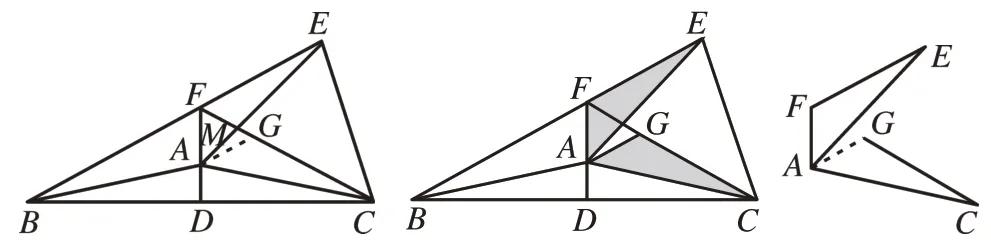
图10
[例5]如图11,在△ABC中,AB=AC,∠ADB=∠BAC=60°,求∠ADC的度数。
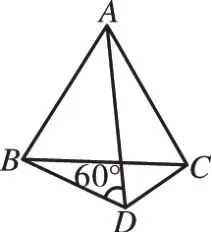
图11
这道题不仅有等边三角形,还有含60°角的三角形△ABD,笔者引导学生思考:能否尝试补短?∠ADB的两边中,BD比较短,可将短边BD延长至E,使DE=AD(如图12),从而形成等边三角形△AED,进而构造了共顶点A的等边三角形△ADE和等边三角形△ABC的“手拉手”模型。

图12
五、作等边三角形构造等边三角形“手拉手”模型
当图形中只有一个等边三角形时,也可以在它的一个顶点作另一个等边三角形,从而构造等边三角形“手拉手”模型。
[例6]如图13,E为等边△ABC内一点,∠BEA=90°,∠AEC=150°,求证:BE=2EC。
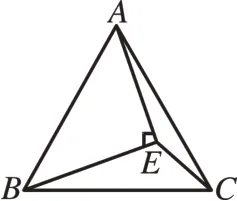
图13
本题可以EC为其中一边在其右侧构造等边△EDC,这样△EDC就与△ABC构成共顶点C的“手拉手”模型(如图14)。
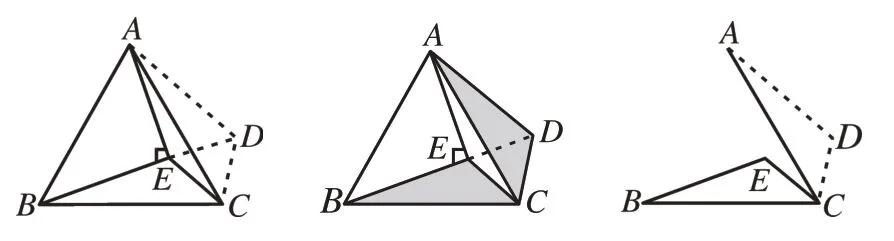
图14
六、“手拉手”模型的应用
笔者在几何综合题的教学实践中,提出了“四步骤几何模型研究”的教学策略(如图15),以帮助学生实现对模型的构造和对综合问题的解决。
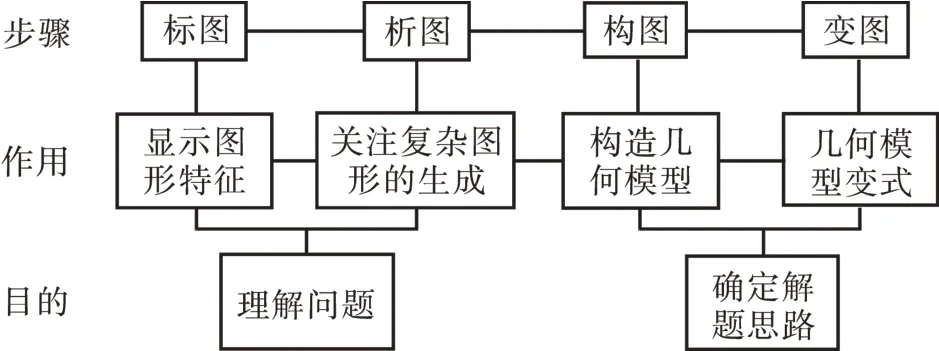
图15
下面以一道模拟题为例说明这个教学策略。
[例7]如图16,△ABC和△CDE都是等边三角形,且点A、C、E在一条直线上,可以证明△ACD≌△BCE,则AD=BE。
(1)将图16 中的△CDE绕点C旋转到图17,猜想此时线段AD与BE的数量关系,并证明你的结论。
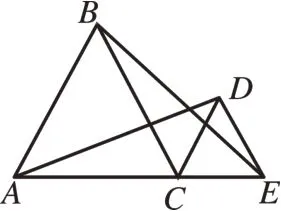
图16
(2)如图17,连接BD,若AC=2 cm,CE=1 cm,现将△CDE绕点C继续旋转,则在旋转过程中,△BDE的面积是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由。
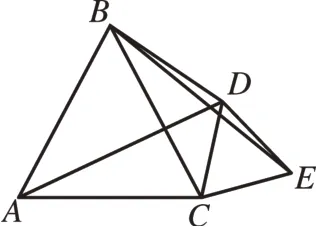
图17
(3)如图18,在△ABC中,点D在AC上,点E在BC上,且DE∥AB,将△DCE绕点C按顺时针方向旋转得到△CD′E′(使∠ACD′<180°),连接BE′,AD′,设AD′分别交BC,BE′于O,F,若△ABC满足∠ACB=60°,BC的值。

图18
分析:
第一步,标图——显示图形的特征。
引导学生标注图形中相等的线段和角(如图19),将图形的特征显性化,为进一步找到等边三角形“手拉手”模型做好铺垫。
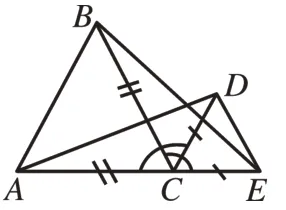
图19
第二步,析图——抽象几何模型。
通过图形标注,学生很容易发现△ACD≌△BCE的条件,即AC=BC,∠ACD=∠BCE,CD=CE(有共顶点的等边三角形),从而发现AD=BE,这对解决第(1)问起到提示作用。如图17 所示的图形虽然A、C、E三点不共线,但学生仍能发现等边三角形“手拉手”模型(如图20),△ABC和△CDE都是等边三角形,所以AC=BC,DC=EC,∠ACB=∠DCE=60°,∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,DC=EC,△ACD≌△BCE,AD=BE。
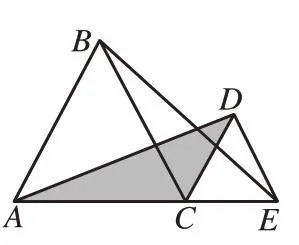
图20
第三步,构图——构造几何模型。
在第(2)问中,将△CDE绕点C继续旋转,当△CDE旋转到BC与C到DE的高在同一条直线上时,△BDE面积最大(如图21),此时,教师应引导学生利用旋转将面积问题转化为“手拉手”模型,再由线段相等得到△BDE是等腰三角形,从而求出△BED面积的最大值。因为DE边上的高为2 +cm,所以△BDE面积的最大值为
图21
第四步,变图——利用图形变化进行模型变化。


图22
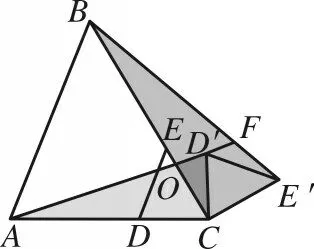
图23
在一道几何综合题中往往会涉及几个不同的模型,在教学中教师应引导学生熟悉模型,熟记相关结论,从题目中快速抽象出几何模型,从而提高学生的解题速度和效率。
从本文的解法归纳中可以看出,即使是比较复杂的图形问题,所用到的也是简单的基础知识,这就要求教师在平时的教学和备考中,从几何图形的形成、变化过程入手进行研究,教给学生几何模型的构建方法,提高学生解题的正确率,增强学生的解题能力。
