抛物线中一类直线过定点问题的探究与推广*

江苏省常州市第二中学(213000) 王 强

圆锥曲线是高中平面解析几何研究的主要对象,平面解析几何的研究方法是通过建立几何图形的代数方程(或不等式),实施代数运算,并由代数运算的结果得到几何图形的性质.类比、联系、特殊化、推广、化归等是数学研究中的常用方法,只要我们善于类比和推广,会发现圆锥曲线中有很多相似的结论,它如同一座金矿等待我们去开采.

定点问题是高考和模考的常考内容,既要求学生具有扎实的学科知识和娴熟的运算能力,又突出呈现对方法的灵活选择和算法的合理优化,能够全面地考查学生数学运算、逻辑推理、直观想象等数学学科核心素养. 2022年扬州市高三期末解析几何解答题考的是抛物线中的一类定点问题,本文对此类定点问题进行了探究与推广,给出了抛物线中的一般化结论,进一步将结论推广到椭圆和双曲线,推广的过程中应用GeoGebra进行了辅助验证.

1 探究由来,横向推广

试题呈现(2022年扬州高三期末考试数学第21题)已知抛物线y2= 2px(p＞0)的焦点F到准线的距离为2.

(1)求抛物线的方程;

(2)过点P(1,1)作两条动直线l1,l2分别交抛物线于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,试判断直线m是否经过定点,并说明理由.

第一问答案为y2= 4x,第二问答案为定点,因第二问是下面定理1当p = 2, x0= 1,y0= 1,的特殊情形,证法相似此处省略证明.

将上述抛物线第二问的结论一般化,得到如下定理1.

定理1设抛物线C : y2= 2px(p＞0), P(x0,y0)是平面上任意一点,过点P作两条动直线l1,l2分别交抛物线于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,则直线m过定点.

证明当过点P的斜率为0时,直线与抛物线只有一个交点,不符合题意.当过点P的斜率不为0时,设直线l1: x - x0= m1(y - y0),直线l2: x - x0=m2(y - y0).联立y2= 2px和x - x0= m1(y - y0)得y2- 2pm1y + 2pm1y0- 2px0= 0.设A(x1,y1), B(x2,y2),则y1+ y2= 2pm1, y1y2= 2pm1y0- 2px0, x1+ x2=m1(y1+ y2- 2y0) + 2x0= 2pm- 2m1y0+ 2x0,

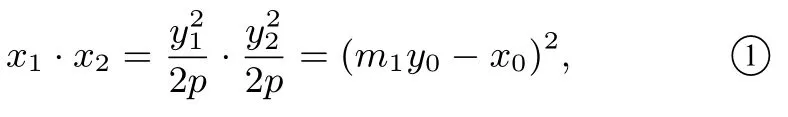
则以AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(yy2) = 0即将式①中的各项代入式②整理化简得

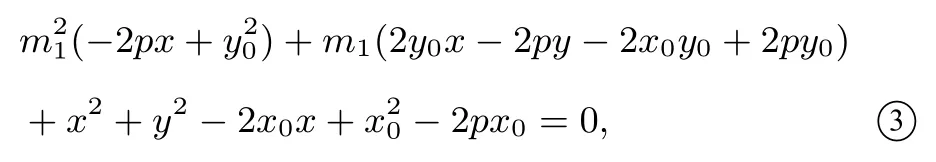
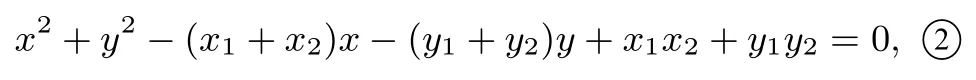
同理,以CD为直径的圆的方程为

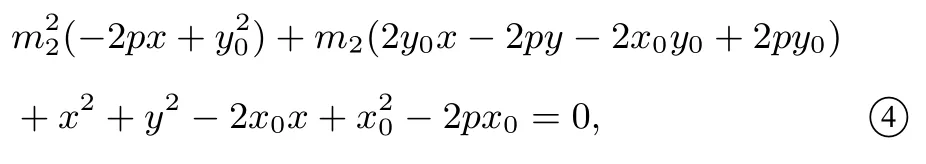
2 纵向推广,完善结论

对于一个好问题,著名教育家波利亚曾这样比喻:“好问题同某种蘑菇有些相像,它们都是成堆地生长的,找到一个以后,你应当在周围找一找,很可能附近就有好几个”.当我们幸运地发现第一朵蘑菇后,可以通过推广、类比、一般化等数学研究方法发现周围更大地蘑菇.我们可以进一步思考,将抛物线换成椭圆或双曲线,是否也有类似的结论,经过探究得到定理2.

定理2设椭圆C := 1(a＞b＞0), P(x,y)00是平面上任意一点,过点P作两条动直线l1,l2分别交椭圆于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,则直线m过定点

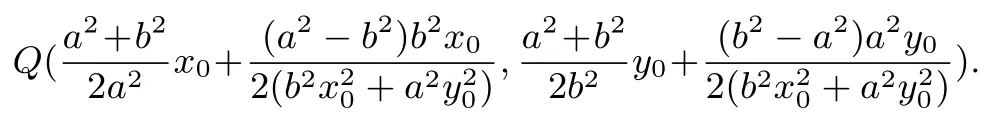
证明当直线l1,l2的斜率均存在且不为0,则设直线l1: y - y0= k1(x - x0)直线l2: y - y0= k2(x - x0),联立= 1(a＞b＞0)和y - y0= k1(x - x0)得

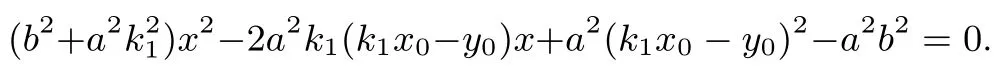
设A(x1,y1), B(x2,y2),则

因为直线l1,l2的斜率均不为0,可设= m,则2直线l1: x-x0= m1(y-y0),直线l2: x-x0= m2(y-y0).联立椭圆C和x - x0= m1(y - y0)得

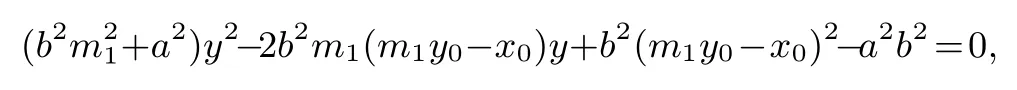
则易得:

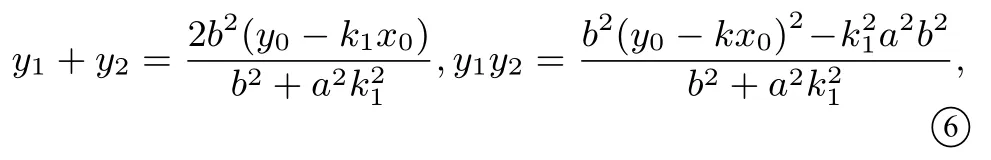
则以AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(yy2) = 0,即

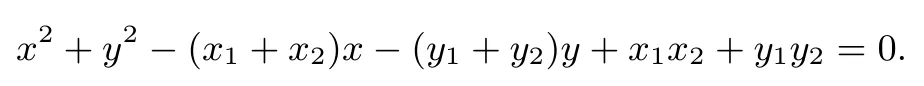
将式⑤和⑥代入整理得式⑦

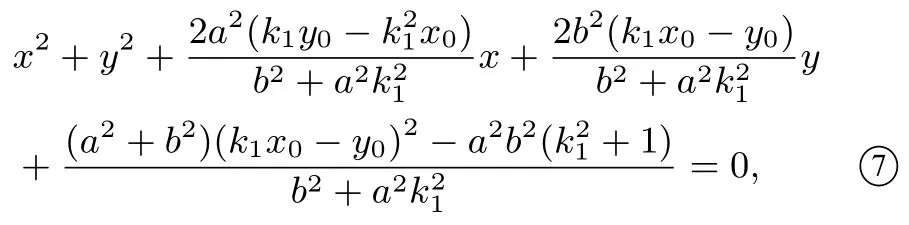
同理,以CD为直径的圆的方程为式⑧

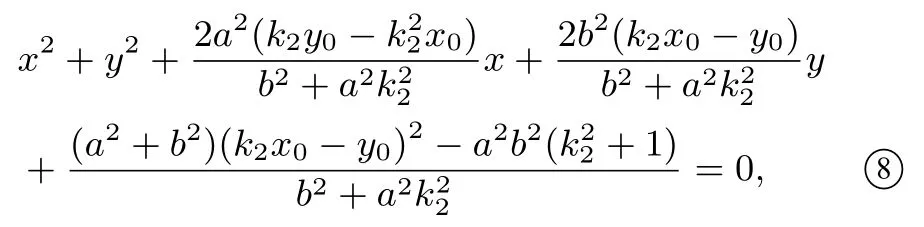
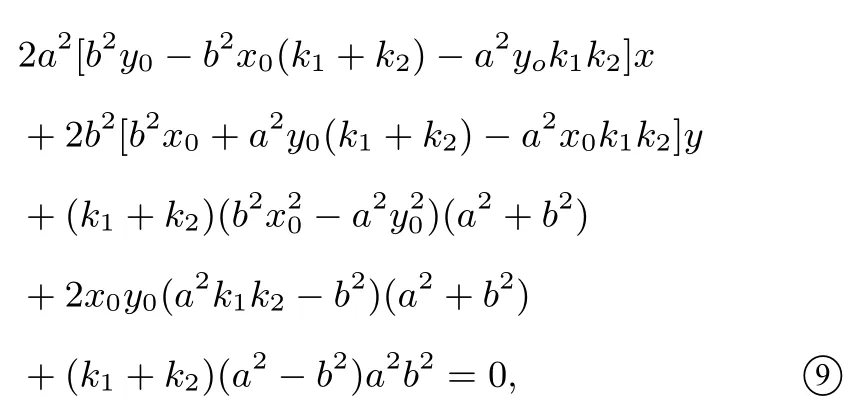
进一步整理式⑨得

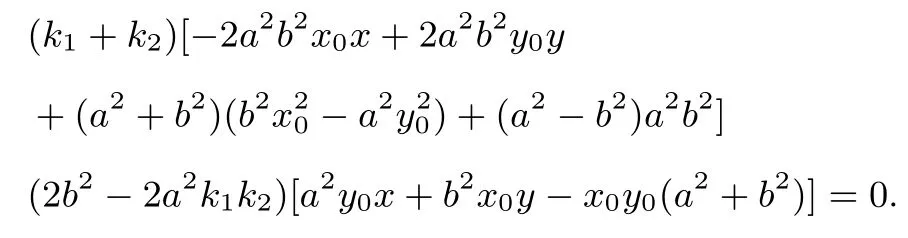
令

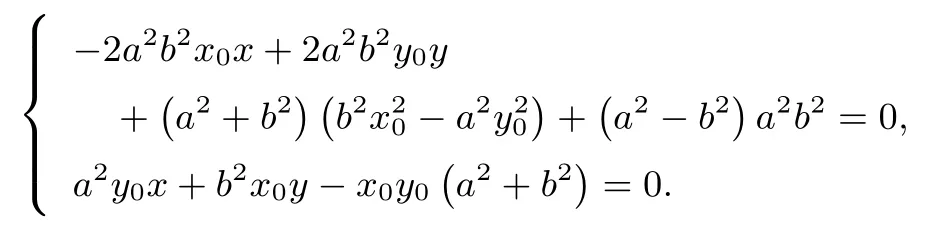
解得

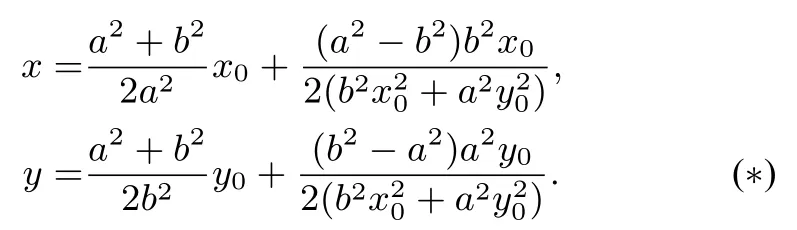
当直线l1或l2的斜率为0时,不妨设l1的斜率为0,此时以AB为直径的圆的方程为x2+(y - y0)2= a2(1-),此方程即是式⑦k = 0时对应的方程.

当直线l1或l2的斜率不存在时,不妨设l1的斜率不存在,此时以AB为直径的圆的方程为(x - x0)2+ y2=,此时结合式⑧,两式相减可得直线m的方程为

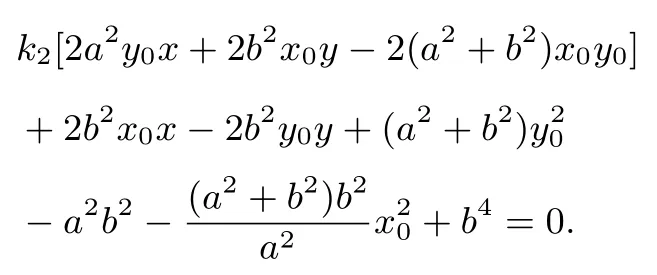
代入(∗)式检验始终满足上面的方程(此处证明不再赘述),因而定理2得证.

特别地,当a = b时,此时椭圆C的方程即为圆的方程,由定理2可推得定理3.

定理3设圆C : x2+ y2= a2(a＞0), P(x0,y0)是平面上任意一点,过点P作两条动直线l1,l2分别交圆于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,则直线m恒过定点P(x0,y0).

3 技术辅助,解后反思

通过进一步研究发现双曲线中也有这样神奇的结论,从而得到下面的定理4,并借助GeoGebra进行了验证,有兴趣的读者可以类比定理2的证明方法推证定理4.

定理4设双曲线C := 1(a＞0,b＞0),P(x0,y0)是平面上任意一点,过点P作两条动直线l1,l2分别交双曲线于点A,B,C,D.设以AB为直径的圆和以CD为直径的圆的公共弦所在直线为m,则直线m过定点

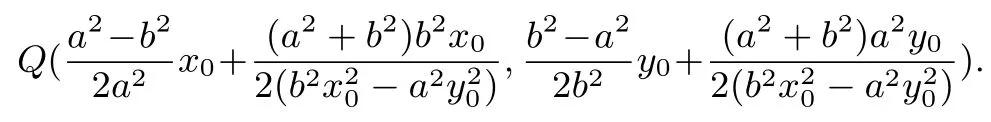
章建跃教授提出“四个理解”是落实核心素养的关键,“理解技术”就是要懂得如何有效利用技术帮助学生的学和教师的教.本探究中充分发挥动态几何软件GeoGebra的辅助功能,在定理猜想中利用GeoGebra的动态呈现功能对一般情况进行验证,发现研究的可行性;在定理证明后利用GeoGebra软件的数值计算功能对定理结论进行验证,确定结论的可靠性.

从这类直线过定点问题的研究中笔者深切感受到GeoGebra软件不仅是一个几何图形动态展示的强大工具,更是一个数学探究学习的有效利器,也为探究性作业的设计和完成提供了自主探究的平台.在新课改中我们应加强提升自身的信息技术素养,更好地利用技术促进教与学,这也是数学教师专业成长的必经之路.