2022年高考乙卷理科第20题的探究与推广

湖北省天门中学(431700) 代成红

一、考题呈现

题目1(2022年高考乙卷理科第20题)已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2),B(,-1)两点.

(1)求E的方程;

(2)设过点P (1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段AB交于点T,点H满足证明:直线HN过定点.

图1

答案(1)= 1; (2)直线HN过定点(0,-2).

二、解法探究

题目1虽然构图简单,但入手并不容易,计算量大,学生得分困难.第(1)问是容易的,以下主要研究第(2)问.

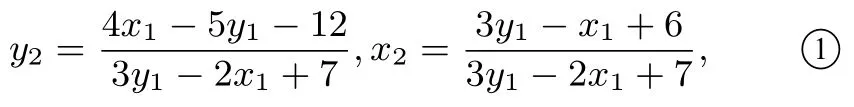
评注考虑直线MN在两个特殊情形下的位置(比如N在A点处、椭圆上顶点处),通过作图可以猜测出直线HN所过的定点为A.因此解法1直接计算截距b为定值,这是典型的先猜后证的做法.即使如此,题1计算量也相当大,对学生直观想象、数学运算等核心素养是极大的考验.

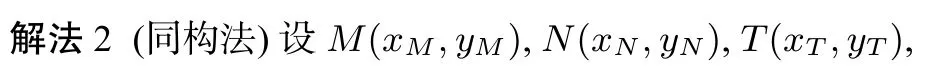
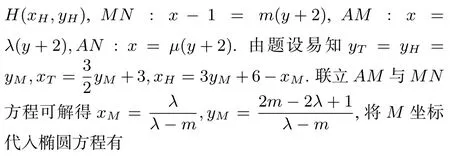
评注(1)从几何元素相互关系来看,点M与点N具有相同的地位,这是同构法能实行的条件;直线AM,AN斜率的倒数和等于3,直线AM,AH斜率的倒数和也等于3是解法2的要点. (2)直线MN,AM,AN的倾斜角可以为不能为0,为了回避分类讨论,三条直线都采用了倒设斜率的方式给出方程.

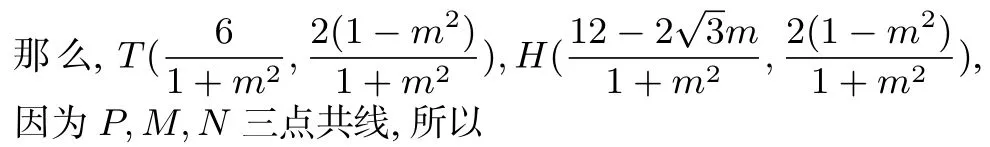
(2)使用椭圆代数形式的参数方程可以直接算出直线HN的方程,从而明确HN经过的定点.不需要先猜后证,运算量小是解法3的两大亮点.

解法4(几何法)过点N作直线NK//MH交直线AB于点K,延长NH交直线AB于A1,交直线AP于A2,设M (x1,y1),N (x2,y2),

图2

在直线MN上取点Q(x3,y3),使,那么由知,

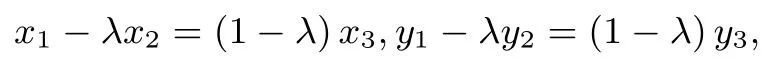
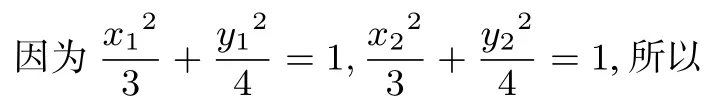
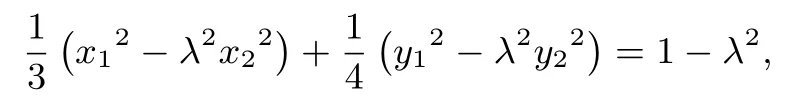
评注解析几何问题终究是几何问题,在解题中适当地使用几何法往往可以收到事半功倍的效果.

三、拓展推广

将题目1一般化,可以得到以下命题:

命题1已知点P (m,-b)(m ≠ 0)是椭圆Γ1:= 1(a＞b＞0)外一点,点A(0,-b),是Γ 上两个不同的点,过P的1直线交Γ1于M,N两点,过M且平行于AP的直线l交直线AB于T,点H是l上的一点,那么T是MH中点的充要条件是直线HN过定点A.

与椭圆类似,双曲线、抛物线也有相似的结果:

命题2已知点P (m,-a)(m ≠ 0,±b)是双曲线1(a,b＞0)外一点,点A(0,-a),是Γ 上两个不同的点,过P的2直线交Γ2于M,N两点,过M且平行于AP的直线l交直线AB于T,点H是l上的一点,那么T是MH中点的充要条件是直线HN过定点A.

命题3已知点P (m,0)(m ≠ 0)是抛物线Γ3: x2=2py (p＞0)外一点,点B(2m,)是Γ上一点, A是坐标3原点,过P的直线交Γ3于M,N两点,过M且平行于AP的直线l交直线AB于T,点H是l上的一点,那么T是MH中点的充要条件是直线HN过定点A.

为进一步地推广,先引入与极线有关的定义定理:

定义1设P是不在圆锥曲线上的点,过点P引两条割线依次交圆锥曲线于四点A,B,C,D,连接AC,BD相交于E,连接AD,BC相交于F,则直线EF为点P对应的极线.若P为圆锥曲线上的点,则过点P的切线即为P点对应的极线.

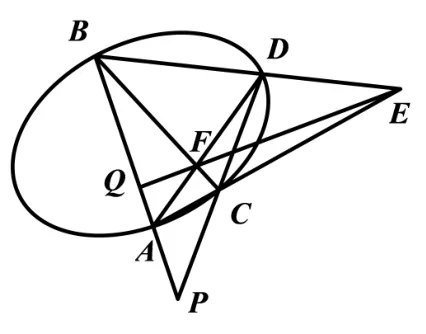
图3

定理1设P是不在圆锥曲线上的点,直线EF为点P对应的极线, EF与过P点的割线AB相交于Q,那么

从极线视角来看,命题1, 2, 3是命题4的特例:

命题4已知点P是圆锥曲线Γ外一点,点P关于Γ的极线交Γ于A,B两个不同的点,过P的直线交Γ于M,N两点,过M且平行于AP的直线l交直线AB于T,点H是l上的一点,那么T是MH中点的充要条件是直线HN过定点A. (参见图4)

图4

证明过点N作MT的平行线交直线AB于S,设直线MN交AB于Q点.

(1)充分性

(2)必要性

在命题4中,如果改变平行线的位置,过P点作AB的平行线与直线AM,AN相交,会得到以下命题:

命题5已知点P是圆锥曲线Γ外一点,点P关于Γ的极线交Γ于A,B两个不同的点,过P的直线交Γ于M,N两点,过P且平行于AB的直线l交直线AM于S,交直线AN于T,那么|PS| = |PT|. (参见图5)

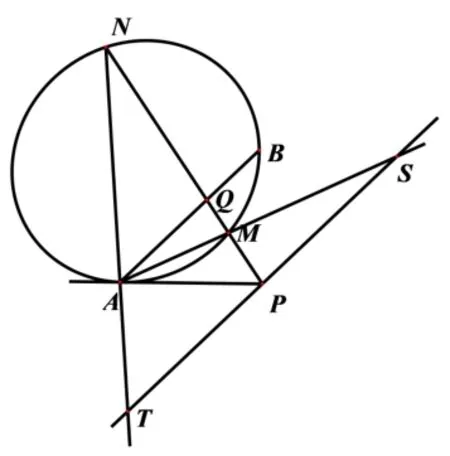
图5

命题5的证法与命题4类似,此处从略.将命题5特殊化,会得到.

题2(2020年北京高考第20题)已知椭圆C := 1过点A(-2,-1),且a = 2b. (1)求椭圆C的方程; (2)过点B (-4,0)的直线l交椭圆C于点M、N,直线MA、NA分别交直线x = -4于点P、Q,求的值.

显然题2与题1背景相同,结构相似,因此题2的解法与题1大同小异,这里就不再赘述了.