巧借抛物线定义 妙解数学综合题

河北省唐山市第一中学

李桂兰

定义是解决相关问题的理论基础和灵魂所在，解题时要善于回归定义和应用定义.抛物线的定义反映了抛物线的本质特征，揭示了曲线存在的几何性质与规律，恰当借助抛物线的定义，能够有效实现抛物线上的点到焦点的距离与它到准线的距离之间的合理转化.一方面可以将抛物线上的点到准线的距离转化为该点到焦点的距离，建构“两点距离”的直观问题；另一方面可以将抛物线上的点到焦点的距离转化为该点到准线的距离，建构“点线距离”的直观问题.根据不同的问题情境，有效转化，合理破解，能起到事半功倍的效果.

1 长度问题

例1[2021届贵州省西南名校联盟(金太阳)高三下学期(3月)开学考理科数学试卷·16]已知抛物线C：y2=6x的焦点为F，准线为l0，过F且斜率为1的直线l与C交于A，B两点(A在B的上方)，过点A作AP⊥l0，垂足为P，点G为∠PAB的角平分线与l0的交点，则|FG|=______.

分析：借助几何视角切入，实现平面解析几何问题几何化，通过抛物线的定义以及几何图形的直观，找出相应的全等三角形，利用两直线垂直的斜率关系确定对应的直线方程，结合交点坐标的确定，并利用两点间的距离公式求解即可.

根据抛物线的定义，有|AP|=|AF|，又∠PAG=∠FAG，所以△PAG≌△FAG.

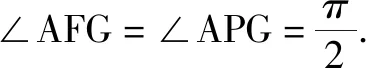
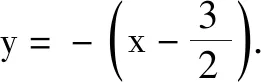
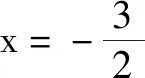
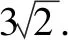
点评：巧妙借助抛物线的定义，实现两线段之间距离的等价转化，这也是抛物线的定义的最基础的应用之一.破解此题的基本思路有两种.①从代数视角出发，设线，设点，联立方程是常规方法；②从几何视角出发，借助几何图形特征与逻辑推理，找到问题的突破口.而观察几何图形的特征，抛物线的定义的应用，可以充分考查学生的直观想象、逻辑推理等核心素养.

2 最值问题

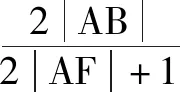
分析：借助条件中点、直线、抛物线的数形结合以及平面几何图形的直观，利用抛物线的定义加以合理转化，通过动点的变化直观确定最值的条件，进而设出切线方程，与抛物线方程联立，消参后建立对应的方程，利用判别式法确定参数的取值，得以求解对应的切点坐标，最后结合两点间的距离公式求解即可.

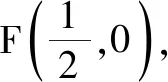
过点B作直线l：x=-1，过点A分别作直线l、抛物线的准线的垂线，垂足分别为C，D，如图1所示.

图1

根据抛物线的定义，可得

设直线AB的方程为x=my-1，将其与抛物线y2=2x联立，消去x并整理，可得y2-2my+2=0.

由判别式Δ=4m2-8=0，可得m2=2.

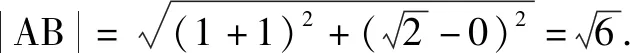
故选：C.

点评：巧妙借助抛物线的定义，合理转化相应的关系式，为利用平面几何图形直观确定最值的条件奠定基础.涉及此类抛物线中一“动”一“静”的两个点的变化问题，关键是利用题目条件“动”“静”结合以及抛物线定义，“动”中取“静”，确定最值问题的位置，为问题的进一步分析与求解指明方向.

3 取值范围问题

分析：直接将交点P的坐标代入已知圆F的方程，通过求解方程来确定参数的取值；利用平面几何图形及抛物线的定义，巧妙将△FAB周长加以合理转化，数形结合直观分析，进而确定其对应的取值范围.

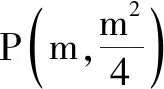
过点A作抛物线Z的准线y=-1的垂线，垂足为D，交x轴于点E，如图2所示.根据抛物线的定义，可得|FA|=|AD|.

图2

所以，△FAB周长为|FA|+|FB|+|AB|=|AD|+2+|AB|=|BD|+2=|BE|+1+2=|BE|+3.

数形结合，可知|BE|∈(1，3)，则△FAB周长|BE|+3∈(4，6).

故填答案：2；(4，6).

点评：巧妙借助抛物线的定义，合理转化三角形的周长，结合线段之间的运算并通过数形结合来确定周长的取值范围.避免代数运算中繁杂的运算过程，更加简单快捷地直达目的，实现问题的巧妙破解，提升解题效益.

在破解涉及抛物线上的点及焦点的一些综合问题时，可以考虑利用抛物线的定义，实现抛物线上的点到焦点的距离与该点到准线的距离之间的合理转化，特别在破解一些抛物线中的长度、最值、取值范围等综合问题中有奇效.利用抛物线定义，回归问题本质，合理转化，巧妙应用，有效掌握数学思想方法和提升数学能力，养成良好的思维品质，培养数学核心素养.