注重通法 揭示本质 落实素养
——以2022年高考数学全国甲卷文科12题的解法研究为例
2022-09-20四川省温江中学
四川省温江中学
张 君 王奋际 张斌辉
1 真题再现
(2022年全国甲卷文科第12题)已知9m=10,a=10m-11,b=8m-9,则( ).
A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a
2 试题分析
罗增儒教授把解题总结为“条件预示可知并启发解题手段,结论预告需知并诱导解题方向”,解题的本质是寻找条件与结论的关系.题从两种角度思考解题方案:一是综合考虑条件与选项,做等价变形;二是直接从条件出发,推导结论.
观察已知条件,a,b均为指数式与常数之差,作差后不易比较大小,又由于a,b无法判断正负,作商也不易比较;再观察选项发现,a,b都需要与0比较.故可考虑等价变形为三个对数值log1011,log910,log89的大小比较,即为思路1.
等价变形为三个对数值的大小比较,此时可以直接作差(解法1)或作商(解法2)比较,也可利用数列单调性(解法3),函数单调性(解法4)或糖水不等式(解法5)比较.解法1~3不约而同地可以使用均值不等式将对数乘法转化为加法,解法4则利用函数求导寻找单调性,解法5需要学生有一定积累.
由于条件中的三个表达式结构类似,可以考虑构造函数,利用函数单调性比较,即为思路2.此时可转化为函数零点和单调性问题(解法6),也可转化为两个函数图象来分析问题(解法7)或指数函数图象的增长速度问题(解法8).
如果将9m作为整体,避开对数运算,适当放缩,那么此题可转化为寻找a的下界和b的上界问题(解法9).
上海市特级教师文卫星老师主张用思维导图对解题思路加以形象总结[1],此题解题思路可表示为如下思维导图(如图1).
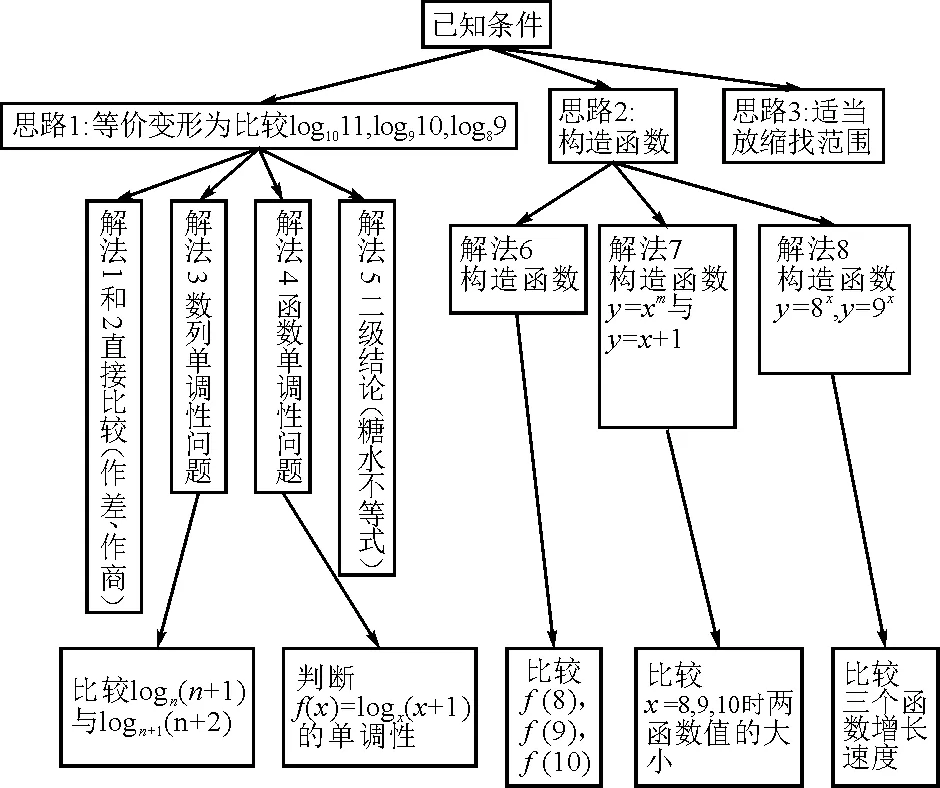
图1
3 一题多解
3.1 综合条件与选项,恒等变形转化
由9m=10知m=log910,比较a=10m-11与0的大小,等价于比较10m与11大小,等价于比较m=log910与log1011大小;同理,比较b=8m-9与0的大小,等价于比较m=log910与log89.至此,本题转化为比较log1011,log910,log89三个数的大小.要比较这三个数有如下几种方案.
解法1:(作差)由于三个对数不同底,考虑化同底之后作差.
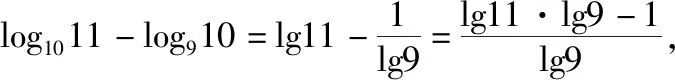
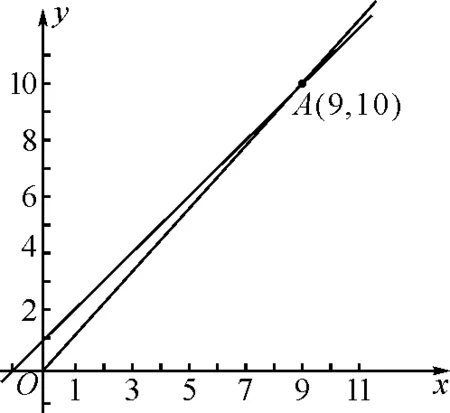
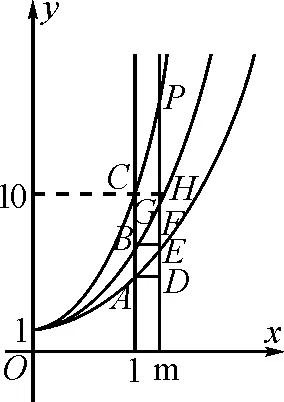
同理可判断log910 故有log1011 解法3:将这三个数看作数列{logn(n+1)}的第8,9,10三项,先研究数列的单调性,比较logn(n+1)与logn+1(n+2)(其中n∈N*,n≥2)的大小. 所以ln2(n+1)-lnn·ln(n+2)>0,即 logn(n+1)>logn+1(n+2). 由此可得log89>log910>log1011.下同解法1. 点评:上述三种方法,先将对数化同底,基于同底对数没有乘法,但可以相加,不约而同地利用均值不等式,最终完成解题. 解法4:令f(x)=logx(x+1)(x>1). 由1 xlnx<(x+1)ln(x+1). 因此,当x>1时,f′(x)<0,所以函数f(x)=logx(x+1)在(1,+∞)上单调递减. 所以f(10) 同理log1011 综上所述,log1011 解法7:令f(x)=xm-x-1(m=log910),则f(9)=0.函数y=xm(m=log910)与y=x+1图象的交点为(9,10),如图2所示. 由图2可知,当0 图2 解法8:如图3,从下到上分别是函数y=8x,y=9x,y=10x的图象,直线x=1与三条曲线分别交于点A,B,C,直线x=m(m=log910)与三条曲线分别交于点E,G,P.分别过点A,B,C作x轴的平行线依次交直线x=m于点D,F,H.因为y=8x,y=9x,y=10x的图象上升速度依次加快,则DE 图3 8m-8<9m-9=1<10m-10, 8m-9<9m-10=0<10m-11. 故选:A. 点评:解法4,6,7,8都构造了函数,但构造的函数各不相同.构造函数后,利用的函数性质也不同.可见,通法之下也有很多变化. 解法9:显然,m>1.依题意可得 所以a>0>b,故选:A. 点评:解法9综合题目条件信息、指数函数单调性,巧妙放缩,达到“秒杀”的效果. (2019年人教A版数学必修第一册第141页第13题)比较下列各题中三个值的大小[2]: (1)log0.26,log0.36,log0.46;(2)log23,log34,log45. 我们来研究一下第(2)问. 所以ln23-ln2ln4>0,即log23>log34. 同理可得log34>log45. 综上所述,log23>log34>log45. 点评:作差、通分后,利用基本不等式即可判断ln23-ln2·ln4的符号.如果掌握了这种思想方法,那么考题中a与b的符号就容易联想到利用基本不等式来判断,这说明这道考题源于课本高于课本.因此,指导高三复习要立足课本,适当拔高,就能提质减负! 国务院《深化新时代教育评价改革总体方案》提出,要“改变相对固化的试题形式,增强试题开放性,减少死记硬背和‘机械刷题’现象”[3],这要求教学中要重视通性通法,寻找解题本质,落实核心素养. 本文对2022数学甲卷文科12题的解法研究中,主要提出了三大类通法:一是综合考虑条件和结论,等价变形后,作差、作商比较大小;二是结构相似,构造函数,利用函数性质,如单调性、图象、增长趋势等比较大小;三是利用放缩、特殊值,甚至泰勒展开等估计参数值的范围比较大小. 这些“通法”当然也能迁移到其他高考题,例如: (1)(2020·全国卷Ⅲ理科第12题)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ). A.a A.a A.c 在高考题基础上,笔者作了一些变式,读者可以尝试从通法入手,完成解题. 变式1已知a=101.1-6,b=91.1-5,c=81.1-4,则a,b,c的大小关系是( ). A.a 变式2已知10m=11,a=8m-9,b=9m-10,则( ). A.a>0>bB.a>b>0 C.0>b>aD.b>0>a 变式3已知9m=11,a=10m-12,b=8m-10,则( ). A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a 变式4已知5m=31,a=6m-42,b=7m-55,则a,b,c的大小关系是( ). A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a 提示:(1)B. (2)C. (3)A. (4)C.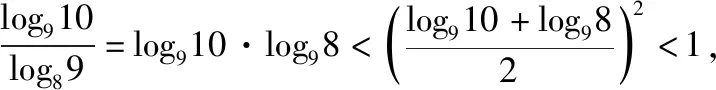
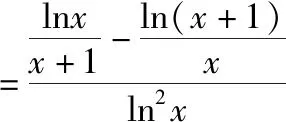
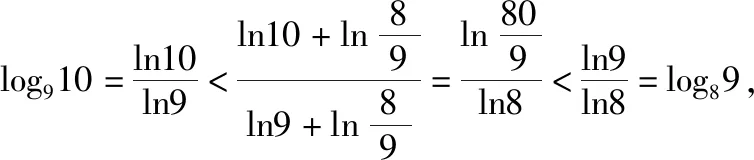
3.2 形式同构,构造函数,逆用单调性,数形结合
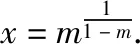
3.3 化异为同,适当放缩
4 课本溯源
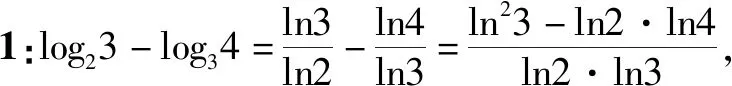
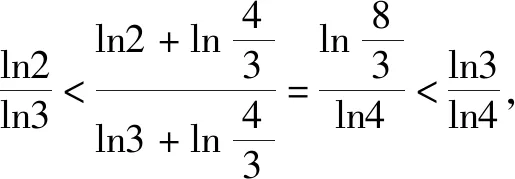
5 通法迁移
6 一题多变
