巧借函数图象 妙解零点问题
2022-09-20江苏省徐州市第三中学
江苏省徐州市第三中学
郭 琪
1 引言
函数的图象从直观角度反映了函数相应的基本性质.在解答选择题、填空题时,可以直接根据函数的图象迅速得出解题方案;在解答题中,也可以从函数的图象上获得一些有用的解题思路.而解答一些函数的零点问题时,借助函数的图象,可以更加直观有效地解决一些与函数的零点个数、零点所在区间等相关数学问题.
2 零点个数判定
涉及较复杂函数的零点个数的判定问题,经常将其转化为方程的实根问题,借助两个函数图象的交点个数情况来分析与直观判定.经常以常见的基本初等函数的图象为转化的根本目标.
例1已知函数f(x)=e-x+x2-3x+1,则函数f(x)的零点个数为( ).
A.3 B.2 C.1 D.0
分析:结合函数所对应的方程的恒等变形转化,将函数的零点问题转化为方程的实根问题,再进一步转化为一个指数函数与一个二次函数图象的交点问题,从而利用数形结合巧妙转化,直观判定.
解析:由f(x)=e-x+x2-3x+1=0,变形可得e-x=-x2+3x-1.
在同一平面直角坐标系内作出指数函数y=e-x和二次函数y=-x2+3x-1的图象,如图1所示.

图1
由图1可知,函数y=e-x和y=-x2+3x-1的图象有2个交点.
所以,函数f(x)的零点有2个.故选择:B.
点评:涉及函数零点的个数判定问题,其实就是对应的方程的实根个数问题,但是直接通过解方程来分析与求解并不容易,而是根据对应函数的图象与性质来直观判断,尤其是那些变形转化后方程两端对应的函数类型不同且均是基本初等函数时,大多用数形结合方法求解与处理.
3 函数取值确定
涉及函数值的正负取值的确定问题时,经常结合函数的零点将其转化为两个函数图象的交点问题,并利用函数图象的上下位置关系来分析与确定相关函数值的正负取值等情况.

A.f(x1)<0,f(x2)<0
B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
分析:结合函数所对应的方程的恒等变形转化,对应函数的零点转化为一个指数函数与一个类似反比例函数的图象的交点位置问题.利用函数图象的位置特征来判断相应函数值的正负取值情况.



图2


因为x1∈(1,x0),x2∈(x0,+∞),所以结合函数的图象直观可知f(x1)<0,f(x2)>0.
故选择:B.
点评:确定此类函数值的正负取值情况时,经常利用函数的单调性来分析与处理.但由于函数解析式的复杂性,不易很快确定函数的单调性.而借助函数与方程的转化,利用两个不同函数图象的交点情况以及图象的上下位置关系来确定对应函数值的正负取值情况,更加直观有效,简捷方便.
4 参数范围求解
涉及含参数的函数的零点或方程的实根问题时,经常将此类问题转化为两个函数图象的交点问题,通过动与静的结合,常量与变量的变换等来合理平移相应的函数图象,数形直观地确定参数取值范围.

A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
分析:结合函数所对应的方程的恒等变形转化,将问题转化为关于x的方程f(x)=-x-a有2个不同的实根,进而结合分段函数f(x)的图象与直线之间一“曲”一“直”,一“静”一“动”的变化情况,利用数形结合,巧妙直观地确定参数的取值范围.
解析:由函数g(x)=f(x)+x+a存在2个零点,即关于x的方程f(x)=-x-a有2个不同的实根,可知函数f(x)的图象与直线y=-x-a有2个交点.
在同一平面直角坐标系中作出直线y=-x-a与分段函数f(x)的图象,如图3所示.

图3
结合图3直观可知,-a≤1,解得a≥-1.
所以,实数a的取值范围是[-1,+∞).
故选择:C.
点评:解决一些涉及含参变量的函数的零点、方程中的实根等相关问题时,经常结合对应代数式的恒等变形,将其转化为两个相关函数所对应的方程,合理分离参数,进而实现一“曲”一“直”,一“静”一“动”,综合利用参数的几何意义,以及变形规律、条件限制等来确定参数的取值情况.
5 复合函数应用
涉及复合函数的零点或复合方程的实根问题时,经常借助函数或方程的恒等变形,将问题转化为相关函数图象的位置关系问题,结合交点情况、位置关系等来综合求解.

A.5个 B.6个 C.7个 D.8个
分析:作出相应分段函数的图象,结合复合方程的求解,将方程不相等的实根的个数,转化为分段函数图象与直线的交点个数问题,结合函数图象特征来直观分析与确定即可.
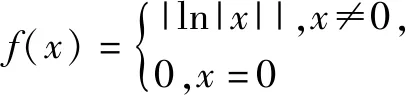

图4
由方程f2(x)-f(x)=0,得f(x)=1,或f(x)=0.
方程f(x)=0的不相等的实根的个数就是函数f(x)的图象与直线y=0(x轴)的交点个数,根据函数图象直观可知,方程f(x)=0有3个不相等的实根;
而方程f(x)=1的不相等的实根的个数就是函数f(x)的图象与直线y=1的交点个数,根据函数图象直观可知,方程f(x)=1有4个不相等的实根.
所以,方程f2(x)-f(x)=0的不相等实根共有7个.故选择:C.
点评:涉及一些复合函数或方程的零点问题,经常借助复合函数或方程的恒等变形与转化,进而综合函数自身的结构特征以及对应的函数图象,数形直观来解决包括函数零点在内的一些基本性质问题,实现函数与方程的巧妙转化、数形结合思想的综合应用等.
6 结束语
利用函数的图象解决有关函数的零点问题时,关键是合理进行代数运算与恒等变形,转化为常见的基本初等函数问题,合理作出对应函数的图象加以直观分析,综合处理.解决此类问题的基本策略技巧是合理分离参数,做到一“静”一“动”,一“直”一“曲”,“动”直线,“静”曲线,巧平移,妙变换.借助函数图象,“直”“曲”分离,数形结合,“动”“静”配合,直观想象,全面提升学生数学品质、数学能力,培养数学核心素养.
