多因素影响下大跨度地下硐室抗爆稳定性分析*

2022-09-20罗军洪刘宏伟林振荣付安琪蔚立元

爆破 2022年3期

罗军洪，刘宏伟，林振荣，付安琪，蔚立元

(1.中国人民解放军空军勤务学院机场勤务保障系，徐州 221000；2.中国矿业大学深部岩土力学与地下工程国家重点实验室，徐州 221116)

随着世界形势的变换和军事技术的不断发展，国防建设工程面临着诸多新的挑战[1]。当今的现代战争中，钻地武器的制导精度越来越高，毁伤效果越来越强，大量的地下防护工程面临直接打击命中的严重威胁，尤其是大跨度的地下硐室(地下指挥所、地下飞机洞库等)更加不利于抵抗地冲击的破坏[2]。因此，深入研究地下硐室在爆炸冲击下的动态响应和破坏机理已成为燃眉之急，对于保障国家安全具有十分重要的战略意义。

现场试验、物理模型试验和数值分析是研究该类问题最常用的手段，其中物理模型试验与数值分析成本较低、可重复性强、可信度高，一直备受专家学者的青睐。在模型试验研究方面，顾金才团队研制出岩土工程抗爆结构模型试验装置[3-5]，并对不同类型锚固硐室的抗爆性能进行了研究。徐景茂等通过模型试验，分析总结了不同加固方式的硐室在爆炸荷载下的受力变形特征和围岩破坏形态[6,7]。陈安敏通过抗爆结构模型试验，分析了爆炸荷载和超载条件下毛洞与衬砌硐室围岩的损伤破坏特征[8]，结果表明衬砌支护能够有效提高硐室的抗爆性能。袁伟泽通过模型试验获得了不同爆炸荷载作用下硐库周边及衬砌的压力、加速度、位移的分布规律[9]。杨自有由模型试验得到了加速度-时程曲线，研究了爆炸条件下不同锚固参数硐室围岩的加速度响应特征[10]。徐干成提出了围岩外交叉锚固方法，并对加固后的硐室模型进行了爆炸试验[11]。史新帅通过自主研制的大尺度三维巷道冲击地压灾变演化与失稳模拟试验系统，对巷道在动静组合下的冲击失稳过程进行了研究[12]。

此外，利用数值分析手段对硐室抗爆能力进行的研究也层出不穷。王光勇基于模型试验结果[13,14]，通过动态数值模拟软件研究了不同方向、不同强度爆炸荷载下锚固硐室中爆炸应力波的传播规律和裂纹形成机理。鞠杨通过LS-DYNA有限元软件分析了爆炸发生时岩层中应力波传递和巷道地板的破坏过程[15]。姚庆等利用LS-DYNA有限元软件研究了埋深和跨度对穹顶洞室变形规律与破坏荷载的影响[16]。王光勇通过FLAC3D数值分析软件模拟了锚固硐室在顶爆作用下的破坏形式和破坏过程[17]。

综上所述，针对毛洞以及各种锚固硐室在爆炸冲击下的动态响应、破坏机理等方面已做了大量的工作，但这些硐室跨度大多处于2.5～6 m之间，矢跨比处于0.25～0.7之间，针对飞机洞库、地下厂房等大跨度硐室(跨度大于20 m，矢跨比小于0.2)的研究还较少。本文基于大跨度硐室抗爆模型试验结果，利用FLAC3D数值分析软件对不同爆炸强度、不同爆破方位作用下不同跨度地下硐室的抗爆性能进行了模拟分析，该研究可为未来地下防护工程的建设提供一定的借鉴。

1 研究方案

本文以浅埋大跨度地下洞室抗爆模型试验为基础，对试验工况进行相应的数值模拟，并将两者结果对比以验证模拟的可靠性，然后改变爆炸强度、爆源位置、硐室跨度等相关参数，以进行多因素影响下的大跨度地下硐室抗爆稳定性分析。

1.1 模型试验方案

原型工程为埋深30 m的直墙拱顶形硐室，跨度为24 m，直墙高3 m，拱高4 m。该硐室防护层为Ⅲ级围岩，衬砌结构层厚度为2 m，采用C40钢筋混凝土。某钻地武器的爆炸威力相当于300 kg当量的TNT炸药，在Ⅲ级围岩中的侵彻深度约为8 m。

模型试验在中国矿业大学的动静组合加载物理模型试验系统上进行，模型的长、宽、高分别为1.2 m、0.3 m和1.2 m。选取低标号水泥砂浆来模拟围岩，配比为砂∶水泥∶水=17∶1.1∶1.8，选取石膏配铝丝网模拟衬砌结构，配比为石膏∶水=1∶1，围岩及衬砌结构的力学参数如表1所示。根据模型尺寸与材料参数确定几何相似比为0.017，密度相似比为0.8，应力相似比为0.014。

试验选择普通导爆索作为爆源施加爆炸荷载，利用瞬发式雷管起爆，采用集中装药的方式，装药密度为1000 kg/m3，根据爆炸应力波峰值相似确定装药量为4.0g当量TNT。本次试验对爆炸应力场、硐壁位移进行监测，压力传感器布置在模型轴向中截面上，具体布置如图1所示，位移传感器U1、U2分别布置在距离硐室洞口100 mm与50 mm处。

表 1 模型围岩及衬砌结构材料物理力学参数

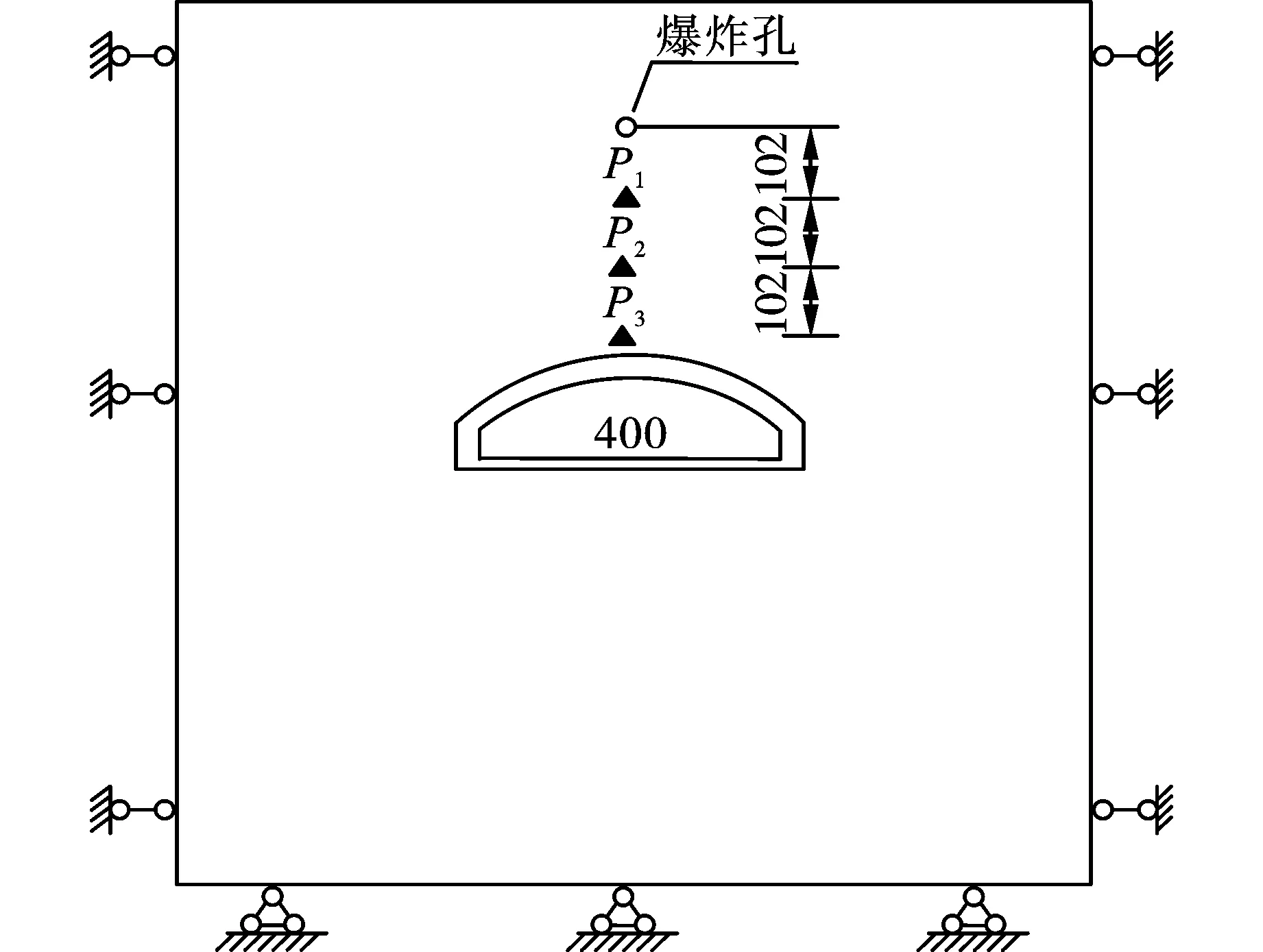
图 1 模型整体示意图Fig. 1 Overall schematic diagram of the model

1.2 数值模拟方案

数值模拟采用FLAC3D有限差分软件开展，计算模型的大小与试验模型的大小相一致，已知材料的静态物理力学参数，根据转换公式可以计算出材料的动态力学参数，列于表2，转换公式具体如下

(1)

(2)

式中：Ed为材料的动态弹性模量；μd为材料的动态泊松比；CS为材料的横波波速；CP为材料的纵波波速。此外，材料的动态抗拉强度取为静态抗拉强度的5倍。

岩体采用摩尔-库伦本构模型，模型的左右、前后边界设置水平方向约束，下边界设置3个方向约束，上边界保持自由，忽略材料自重对应力波传播的影响，在约束边界上施加独立阻尼器的黏性边界，根据FLAC3D动态计算的特点，把动载荷以等效应力的方式加载于爆点球腔内壁的网格节点上，根据爆炸荷载计算公式以及爆炸参数，获得单孔炸药爆炸的脉冲荷载作用时程曲线，如图2所示。

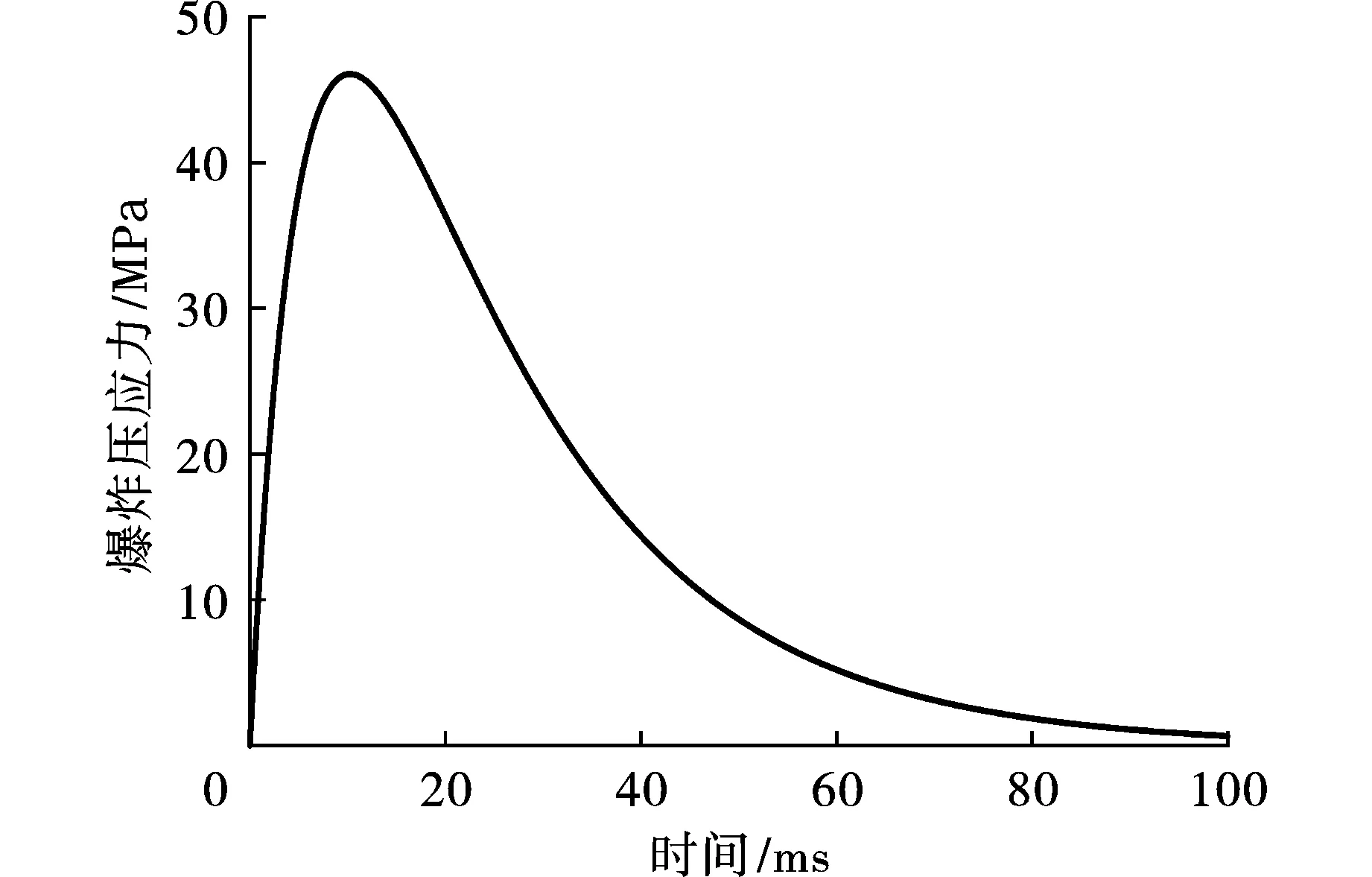
图 2 爆炸脉冲荷载作用时程曲线Fig. 2 Time-history curve of explosion pulse load

利用模型M1对试验过程进行模拟，硐室尺寸、测点布置、爆炸荷载施加均与试验相一致，试验中4.0 g TNT对应的爆炸峰值为46 MPa。在此基础上依次改变爆炸强度、硐室跨度以及爆源位置，具体工况如表3所示。

表 2 模型材料动态计算参数

2 数值模拟与试验结果对比分析

图3为模型M1取自相同测点P1处的试验和数值模拟压应力时程曲线对比图。从图中可以看出：试验和数值模拟压应力时程曲线在形态上是相似的，都是先快速上升到达峰值，然后下降，最后在零点附近振动趋于平衡。总体来看，模拟与试验曲线特征具有较好的一致性，说明数值仿真结果具有较高的置信度，该数值计算模型可以很好地对试验工况进行模拟。

图4是爆炸应力波作用下模型M1硐室围岩应力和塑性区的变化规律图，图5是爆破后模型破坏形态。由图可知：应力波施加之后，炮孔处围岩在极短时间内产生塑性区，并呈球形对称分布；而后压应力波继续呈球面向四周传递，围岩中的压应力值开始逐步增大，当应力波传播至上边界时发生反射，形成拉伸波，使炮孔上方区域产生受拉屈服，模型试验结果也显示地表周围因受拉产生了明显的“层裂”破坏。同理，压应力波向下传播到硐室自由面后发生反射会导致拱部岩体受拉破坏，而图4显示硐室周围并未产生塑性区，这是因为应力波在岩石介质中传播时强度会快速衰减，其强度不足以使岩体破坏，图5显示硐室周围未出现裂纹，硐室仍处于稳定状态。

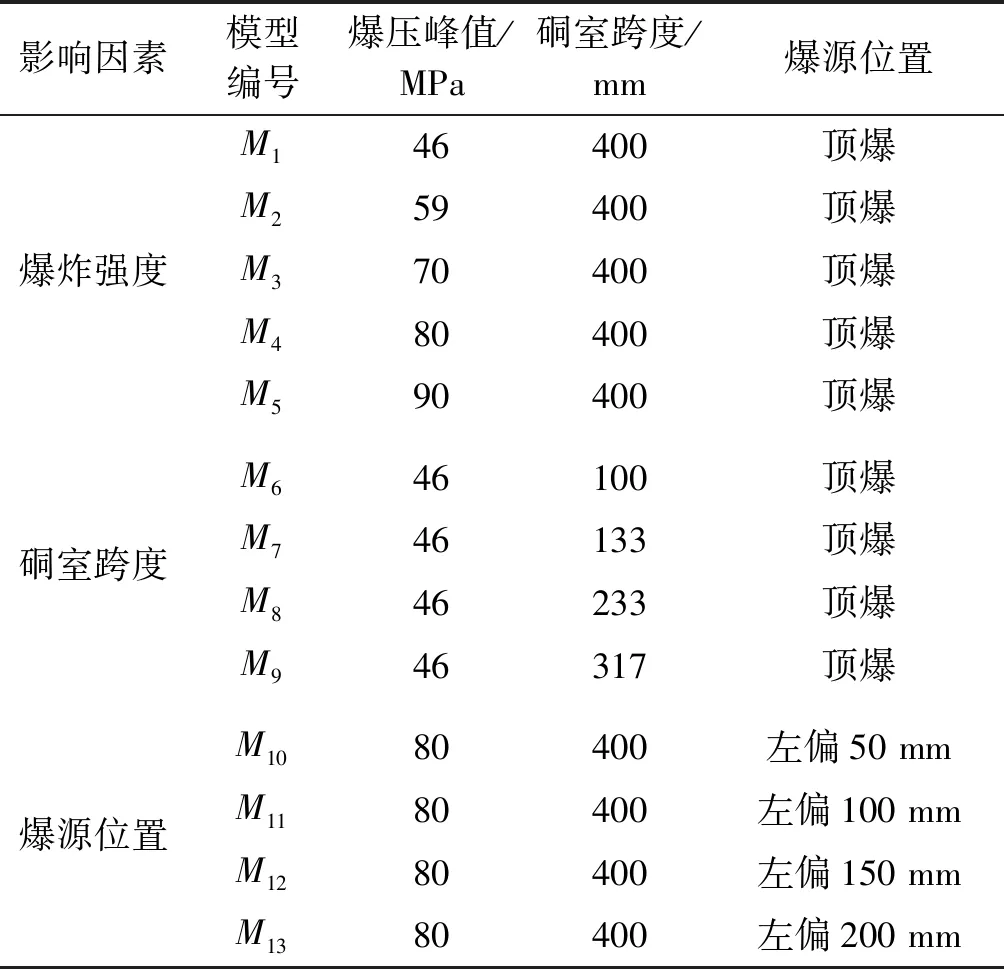
表 3 模拟工况汇总

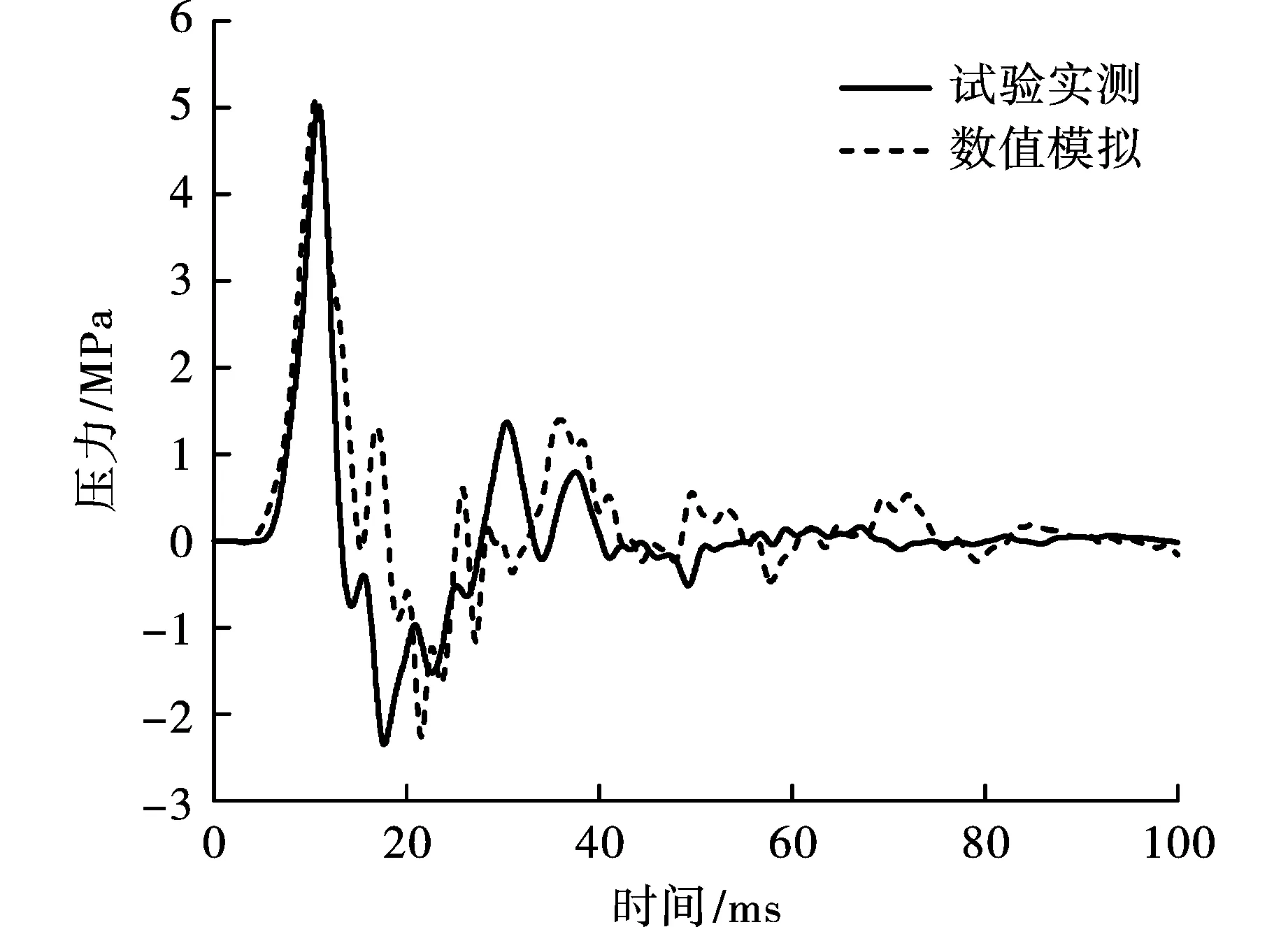
图 3 模型M1 P1测点试验实测与数值模拟曲线对比Fig. 3 Comparison of measured and numerically simulated stress wave curves of model M1 in P1 test

3 不同爆破条件下模型动态响应规律

3.1 不同强度顶爆作用下模型动态响应规律

图6为5种不同爆炸强度下模型最终的状态图，由图对比可知：随着爆压峰值的增大，炮孔周围的受压区域与塑性区体积逐渐扩大，即爆炸强度越大，爆腔越大。除此之外，随着爆压峰值的不断增加，硐室上方的受拉区域不断扩大，但值得注意的是侧墙周围的受拉情况并不严重，这一方面是因为经绕射、反射到达侧墙的应力波强度不足以使岩体受拉；另一方面，该硐室跨度大，侧墙低，应力波对该区域的影响范围较小。而侧墙底部由于硐室的反射和绕射对该区域衰减影响并不明显，因此该处易受拉剪破坏出现裂缝，这与实际情况相吻合。

图 4 模型M1最大主应力、塑性区和竖向位移分布图Fig. 4 Distribution of maximum principal stress,plastic zone and vertical displacement of model M1

硐室上方和拱脚处是较易出现裂纹的区域，地表反射拉伸波与硐室拱顶反射形成的拉伸波会在炮孔下方相遇并发生叠加，使硐室上方围岩产生大量的“八字形”裂缝[18]，当爆炸强度继续增加时，硐室上方拉剪塑性区会连成一片，衬砌结构塑性区也不断扩展，此时硐室可能会出现塌落。

不同爆破强度下应力测点峰值的变化规律如图7所示，由图可知：爆压峰值由46 MPa增加到90 MPa，P1～P3应力峰值分别增加了134%、139%、120%；爆压峰值为46 MPa时，P1测点应力峰值是P3测点的4.25倍，爆压峰值为90 MPa时，P1测点应力峰值是P3测点的5.9倍，这说明应力波在围岩介质中传播时会发生较大程度的衰减。硐室拱顶变形规律如图8所示，由图可知：爆压峰值越大，位移越大；爆心距越小，位移越大。爆压峰值为46 MPa时，U1、U2测点对应的峰值分别为0.29 mm、0.17 mm，爆压峰值增加到90 MPa时，两测点峰值为0.8 mm、0.5 mm，分别增加了1.7倍、1.9倍。

图 5 试验模型破坏形态Fig. 5 Failure mode of test model

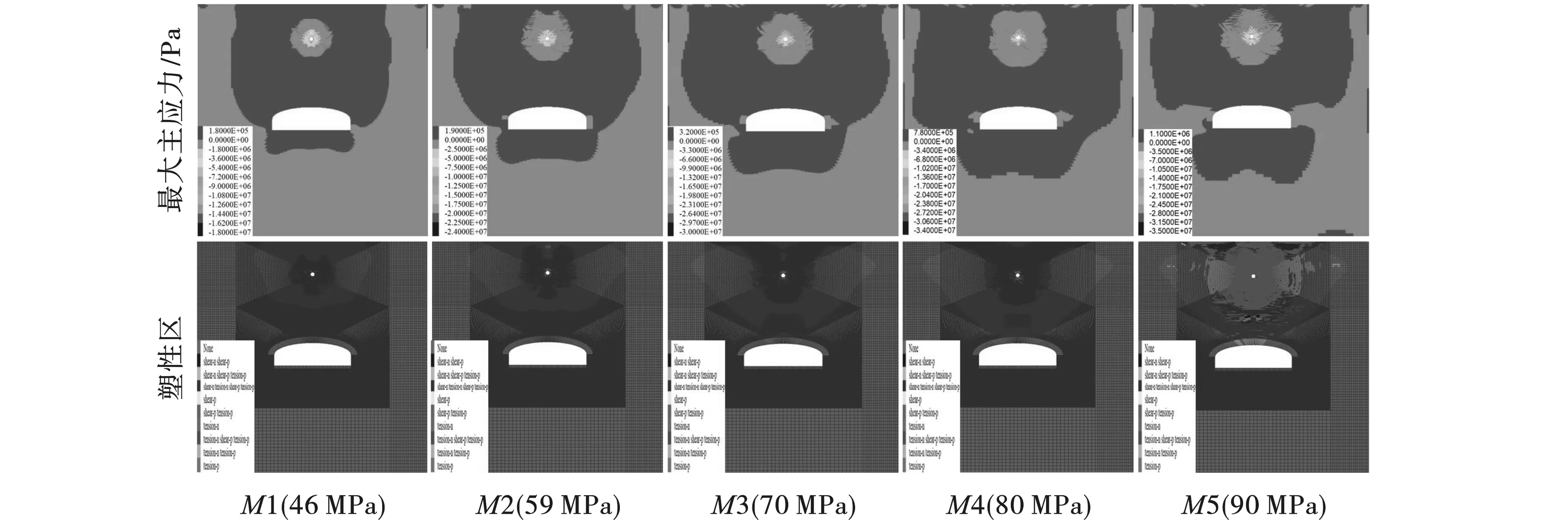
图 6 不同爆压峰值下模型主应力和塑性区最终状态图Fig. 6 Final state diagram of maximum principal stress and plastic zone under different explosion pressure peaks

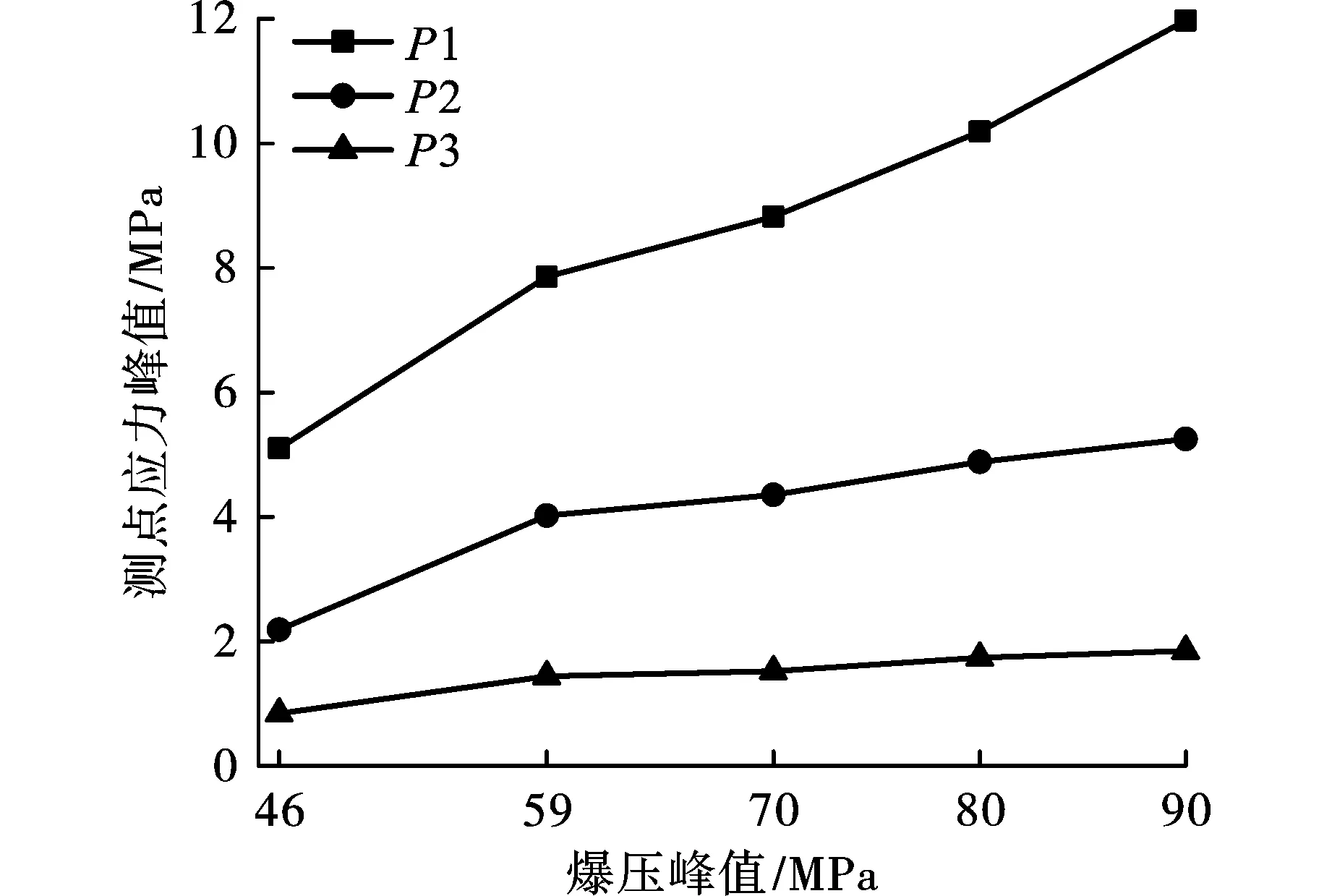
图 7 应力测点峰值随爆压峰值的变化规律Fig. 7 Variation law of peak values of stress test points with peak values of explosion pressures

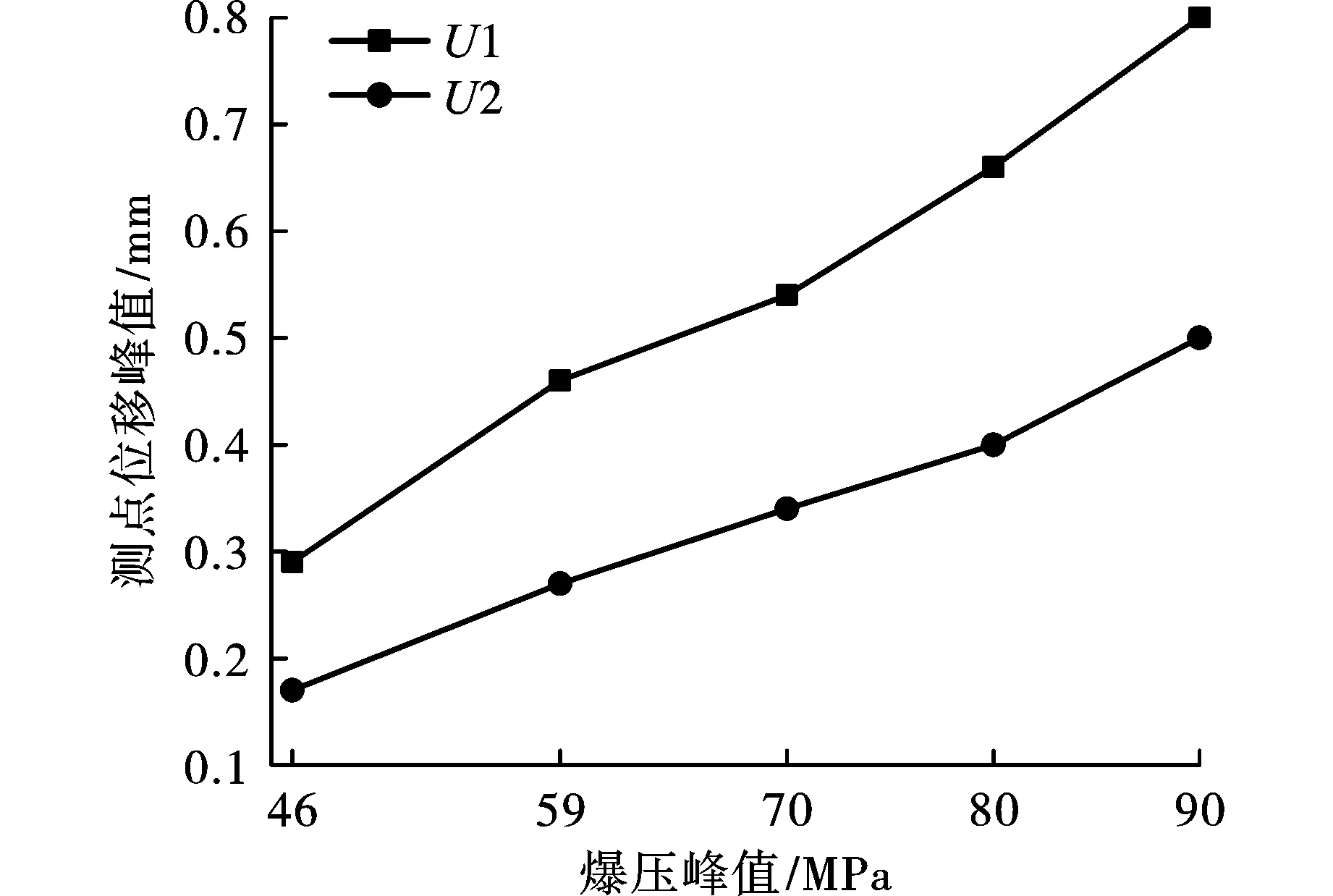
图 8 位移峰值随爆压峰值的变化规律Fig. 8 Variation law of peak values of displacements with peak values of explosion pressures

由以上分析可知采用强度较大的衬砌结构或加长加密的锚杆对硐室表面及拱脚进行加固可提高抗爆性能[6]，增加稳定性。除此之外，增加硐室埋深也可减弱爆炸作用对硐室的损伤和破坏。

3.2 顶爆作用下不同跨度硐室模型动态响应规律

本次模拟分析了在相同的顶爆作用下5种不同跨度硐室的动态响应规律，最终状态如图9所示，由图可知：5个模型炮孔上方围岩受拉区域与塑性区并无明显差别，说明硐室跨度对炮孔上方应力波的传播并无影响；炮孔下方围岩的受力区域随硐室跨度的变化而变化，当跨度为100～233 mm时，硐室临空面过小，影响不了应力波的传播趋势，整个模型的受拉区域主要是由地表反射的拉伸波导致。当硐室跨度足够大时，临空面会阻挡压应力波的传播使其发生反射，此时整个模型的受拉区域由多种反射拉伸波与绕射拉伸波导致。

图 9 不同跨度硐室模型最大主应力和塑性区最终状态图Fig. 9 Final state diagram of maximum principal stress and plastic zone of chambers with different spans

顶爆作用下不同跨度硐室模型应力测点峰值的变化规律如图10所示，拱顶变形规律如图11所示。分析可知：各测点应力峰值随硐室跨度的变化较小，但当硐室跨度由100 mm增加到400 mm，两位移测点峰值分别增加了1.63倍和3.25倍。说明硐室跨度越大，拱顶变形越严重，硐室抗爆性能越差。

图 10 应力关键点峰值随硐室跨度的变化规律Fig. 10 Variation law of peak values of stress test points with different chamber spans

3.3 不同爆炸方位作用下模型动态响应规律

5种不同爆炸方位作用下模型最终状态如图12所示，对比可知，随着炮孔位置向左偏移，逐渐形成自左上角到右下角的受拉带；5个模型衬砌结构均出现了塑性区，但随着炮孔左偏，塑性区域逐渐变小；炮孔左偏后仍会形成“八字形”裂纹，但与顶爆作用不同，该“八字形”两区域内的裂纹程度有明显差异，拱顶上方迎爆区域的裂纹会更严重，且炮孔越往左偏，该现象越明显。

图 11 位移峰值随硐室跨度变化规律Fig. 11 Variation law of peak values of displacements with different chamber spans

图13是测点应力峰值随炮孔偏移距离的变化规律，由图可知：随着炮孔左偏距离的增大，测点爆心距增加，其应力峰值减小，但减小的幅度不大。炮孔偏移对拱顶变形的影响规律如图14所示。由图可知：随着炮孔左偏距离的增大，拱顶变形逐渐变小，从顶爆到炮孔左偏200 mm，测点U1、U2的位移峰值减幅分别为60.6%和75.0%。