薄基体装甲钢弹击侵彻行为与极限抗弹性研究*

官计生，李德发，郭 逊，梁思诚，黄 锋

(1.武汉科技大学 省部共建耐火材料与冶金国家重点实验室,武汉 430081;2.宝钢股份 中央研究院 厚板所,武汉 430080;3.武汉理工大学 湖北省汽车零部件先进技术重点实验室,武汉 430070)

装甲钢具备高强度、高韧性、高硬度以及合理淬透性等优点，100多年来一直被广泛用作坦克等特种车辆车体的结构与防护材料[1]。自装甲钢问世以来，运用实弹射击考核、数值模拟或两者相结合的方法，对其弹击侵彻过程与失效机理就进行了广泛深入的研究，不仅从力学角度探索了其宏观本构规律，亦从微观组织上考察了组织变化对其防护性能的影响，进而通过对合金成分、冶炼工艺与热处理工艺的优化，使装甲钢综合性能得到了很大提高[2-5]。

近年来，为满足城市巷战中轻型特殊车辆机动性和防护性(可近距离抵御轻武器袭击)的需求[6]，薄基体装甲钢得以广泛应用，国内外对此进行了大量研究，开发了一系列性能优良的装甲钢。随着军方战技指标的不断提高，相应装甲钢抗弹性能富余量正不断被压缩。如何准确确定装甲钢极限抗弹性能，对于提高产品合格率、缩短研发周期具有重要意义。针对于此，本文综合打靶实验测试与计算机模拟仿真，以某4.6 mm薄基体装甲钢抗53式7.62 mm普通钢芯弹性能为研究对象，分析其弹击侵彻行为及极限抗弹性能。

1 实验方法与结果

1.1 准静态与动态压缩实验与结果

为对靶材抗弹性进行仿真分析，不可避免地需了解该靶材的相应力学性能参数，以对仿真模型进行材料参数赋值，故首先需对靶材进行准静态与动态压缩性能测试。本研究中，准静态与动态压缩实验所用试样均为取自靶材的直径为4 mm、厚4 mm的小圆柱，且试样厚度方向与装甲钢板厚度方向一致。其中，准静态压缩在电子式万能材料试验机(INSTRON5985)上完成，测试加载速率为0.004 mm/s(即名义应变率为1×10-3s-1)，测试所得靶材准静态压缩应力-应变曲线如图1(a)所示；动态压缩实验在压杆杆径为16 mm、长1000 mm的霍普金森压杆试验装置上进行，所得不同应变率下靶材的应力-应变曲线如图1(b)所示。需要指出的是，图1所示应力-应变曲线均为靶材压缩过程中的工程应力-应变曲线，即纵坐标均为工程应力(s)，横坐标均为工程应变(e)。在后续材料压缩性能参数计算过程中，首先需利用式(1)与式(2)将其转换为相应条件(准静态与动态)下的真实应力(σ)与真实应变(ε)间的关系曲线。

σ=s(1-e)

(1)

ε=-ln(1-e)

(2)

1.2 本构方程确定

(3)

(4)

表 1 靶材J-C模型参数

1.3 打靶测试与结果

在自然温度条件下，采用7.62 mm弹道枪，配备53式7.62 mm普通弹，对440 mm×420 mm×4.6 mm靶板进行不同射距下的打靶测试，为提高测试数据可靠性，每一射距下均打靶三次，并求取平均值以表示相应射距下靶材的抗弹性能。测试发现，各射距下靶材均未被击穿，相应弹坑深度与背凸高度测试结果如表2所示。由表中不难看出，除60 m外，随着射距的降低，弹击后靶材弹坑深度与背凸高度均呈现出增大的趋势。其中，60 m射距时出现的高弹坑深度与背凸高度可能是由于相应打靶测试误差及靶材性能不均(如60 m射击区域正好位于靶材相对较软或存在热处理残留拉应力处)所致。

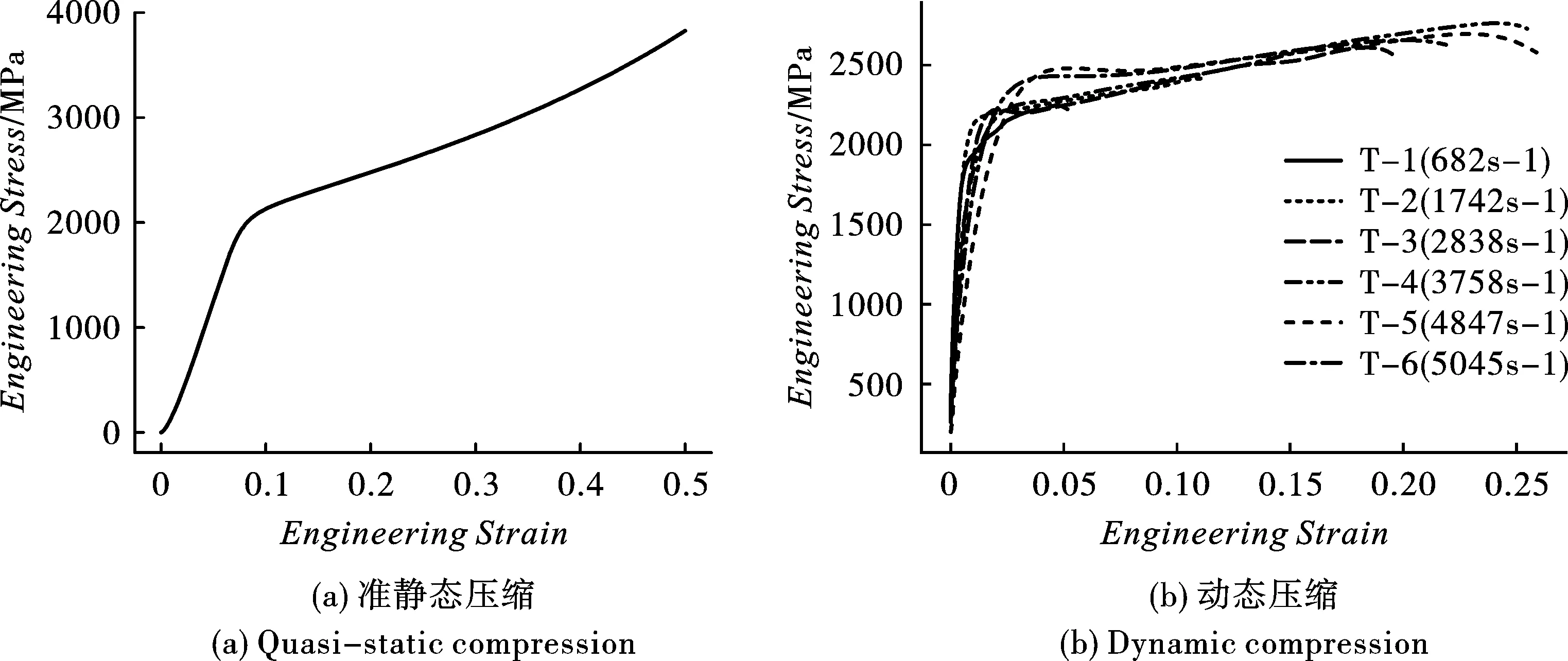
图 1 压缩工程应力-应变曲线Fig. 1 Engineering stress-strain curves of compression

表 2 打靶测试结果

2 仿真分析

2.1 模型建立与有效性验证

根据参考文献[10]，53式7.62 mm普通钢芯弹的结构与相应尺寸参数如图2所示，其由弹盖、弹芯、弹壳及弹拖四部分组成，其中弹体的质量为10.5～10.7 g，弹芯质量为5 g左右。结合图2所示弹型参考参数(图中参数单位为mm)，设定靶材尺寸为80 mm×80 mm×4.6 mm，于Solidworks中建立简化抗弹性仿真三维模型，如图3(a)所示。随后，将以上建立的几何模型(图3(a))文件导入HyperMesh中进行网格剖分，即可得到相应抗弹性仿真分析的有限元模型，如图3(b)所示。其中，为确保仿真精度前提下降低计算机时，在子弹头与靶材接触部位网格较密，而其余非变形区域可适当减少网格数。

由于在建模过程中采用了实体单元，计算中涉侵蚀接触算法，为确保计算正常进行，有时会自动增加某些部件质量，即随计算进行整个模型质量有所变化[11]，一般要求质量变化不得超过5%。图4所示为本模型弹击仿真运算中总质量变化。如图所示，模型初始总质量约为0.262 kg，随着计算的进行，总质量稍有减少，其最小值为0.256 kg，即质量最大变化率为2.3%，满足不超过5%的基本要求。

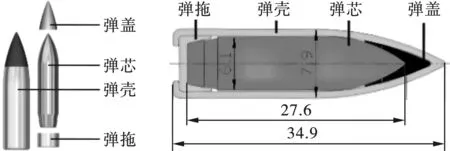
图 2 53式7.62 mm普通钢芯弹结构与参数(单位：mm)[10]Fig. 2 Structure and parameters of 53 type 7.62 mm steel core bullet(unit:mm)[10]

除质量外，由于单元刚度矩阵中秩不足，计算过程中还存在发生沙漏现象的可能。较大的沙漏能会导致仿真精度降低，甚至计算结果完全不可信[12]，因而一般要求沙漏能与系统总能量之比不超过5%。图5所示为本模型仿真计算过程中的能量变化。如图所示，仿真计算过程中系统总能量基本守恒。弹击开始，子弹与钢板发生接触，两者变形耗散能量，动能快速减小并转化为内能，在0.07 ms后动能和内能曲线趋向平稳。由图中系统沙漏能变化曲线可知其最大值为100 kN-mm，约占系统总能量的2.7%，满足低于5%的要求。

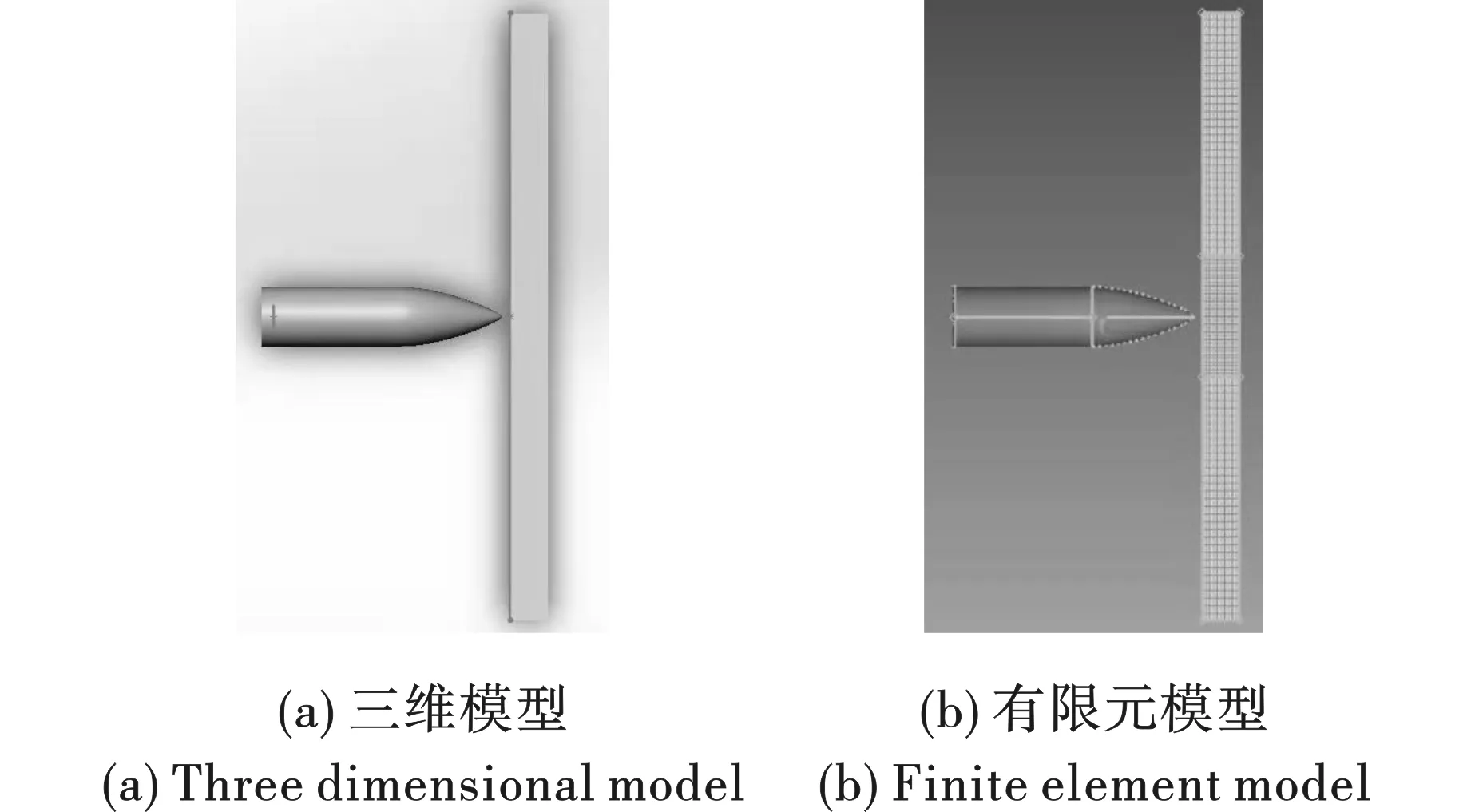
图 3 抗弹性仿真分析模型Fig. 3 Ballistic performance simulation analyzing models

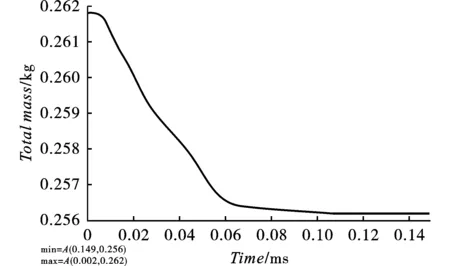
图 4 所建模型弹击仿真过程总质量变化Fig. 4 Total mass change of the built model during projectile impact simulation

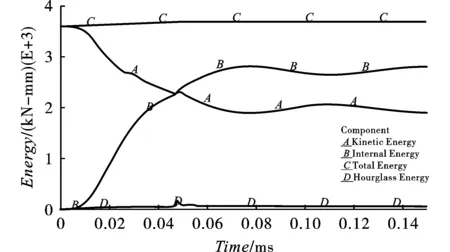
图 5 所见模型弹击仿真过程能量变化Fig. 5 Energy change of the built model during projectile impact simulation

综上，系统总质量和总能量基本维持不变，能量转化曲线平滑过渡，无突变发生，较好地模拟了弹击过程，表明整个有限元模型的网格划分、接触设置、沙漏控制等求解设置均比较合理，所建立的弹击仿真有限元模型计算结果有效可信。

2.2 弹速对侵彻行为影响

图6所示为53式7.62 mm普通钢芯弹以825 m/s的速度冲击该4.6 mm厚靶材时的实时剖面应力云图，图7所示为相应弹击过程中弹体速度变化。由图中可以看出，随着弹体的侵入，靶板发生塑性变形，应力逐渐增大，而弹体速度逐渐衰减。在t略大于0.08 ms时，弹体速度衰减为零，随后在靶材弹性特性作用下发生一定回弹，弹体速度为负，靶材应力有所衰减。值得注意的是，与实际打靶测试一致，在该弹击条件下靶板仅产生塑性变形而未被完全破坏。

图 6 弹击过程实时剖面应力云图Fig. 6 A sequence of sectional plots showing the effective stress of impacting

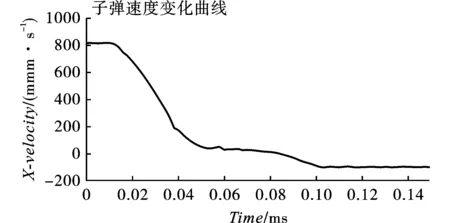
图 7 弹击过程弹体速度变化Fig. 7 The speed curve of bullet during projectile impacting

由于在实际打靶过程中弹速测量均是离出膛口25 m处的弹速v25(均为830 m/s左右)，其与本仿真中弹体接触靶材瞬时弹速825 m/s很接近，因此从弹速出发，可将以上打靶测试中射距为40 m时的弹击条件与本仿真条件近似视为相同。提取仿真计算弹坑深度与背凸高度分别为5.3 mm与3.5 mm。如表2所示，实际打靶射距为40 m时相应弹坑深度与背凸高度分别6.13 mm与3.97 mm。对比发现，相较于实际打靶测试，该条件下仿真计算所得靶材弹坑深度与背凸高度的计算精度分别为86.5%与88.2%。

表3所示为仿真计算所得该靶材在不同弹速下的弹坑深度与背凸高度。为进一步直观分析弹速对抗弹性参数的影响规律，对表3所示数据进行绘图，如图8所示。由此不难看出，弹击后靶材弹坑深度(D)和背凸高度(H)与弹速(v)均近似成线性正比关系，即随着弹速的增加，D与H均近似线性递增。然而，根据能量守恒，靶材受弹击后其弹坑深度与背凸高度理论上应与弹速平方(子弹动能)成线性正比，即与弹速v成抛物线关系，显然这与表3和图8中所示的线性关系不符。为此，对弹速平方(v2)与D和H的关系同样进行了分析(如表3与图8所示)，结果显示，与理论预期一致，D和H与v2近似成线性正比关系。

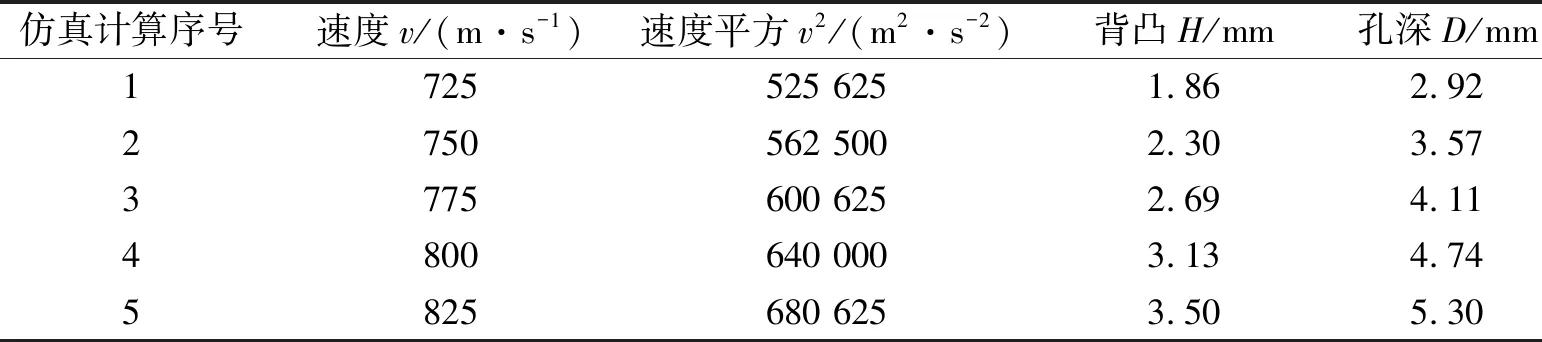
表 3 不同弹速下靶材的抗弹参数

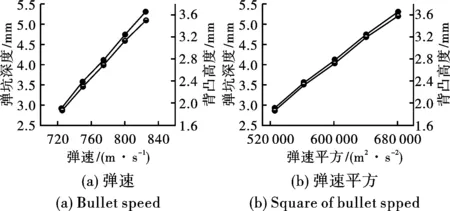
图 8 子弹状态对该靶材抗弹参数的影响Fig. 8 Influence of bullet state on ballistic performance parameters of target plate

利用最小二乘法，对表3所示仿真结果分别进行一元线性拟合，即可获得该靶材弹击后弹坑深度(D)与背凸高度(H)受弹速(v)和弹速平方(v2)影响的数学预测模型，其分别如式(5)至式(8)所示。需要指出的是，虽然理论上D和H应与v2成线性正比，即两者与v成抛物线关系，但在某一区间(如本研究考察弹速范围内)，两者与弹速v间的线性度可以很好，即在该区间内可呈现出良好的线性关系，这与弹击过程能量守恒理论并不相背，且从另一角度表明在该弹速范围内靶板变形主要受弹击冲击力影响。

D=-14.255+0.02372v

(5)

D=-5.077+1.52939×10-5v2

(6)

H=-10.045+0.01644v

(7)

H=-3.683+1.05988×10-5v2

(8)

为利用以上拟合出的数学模型预测该靶材可承受的极限弹速，尚需了解靶材被击穿时的弹坑深度与背凸高度。对此，利用以上所建立有限元模型，在弹速为1100 m/s下重新进行抗弹性仿真分析，计算所得弹击过程中弹坑深度与背凸高度变化曲线分别如图9与图10所示。由图中不难看出，靶材被击穿前，其弹坑深度与背凸高度所达最大值分别为9.2 mm与7.5 mm。

将最大弹坑深度(9.2 mm)代入相应预测模型(式(5)与式(6))，计算得该靶材可承受的极限弹速分别为989 m/s与966 m/s；将最大背凸高度(7.5 mm)代入相应预测模型(式(7)与式(8))，计算得该靶材可承受极限弹速分别为1067 m/s与1027 m/s。由此不难看出，由弹速平方模型(式(6)与式(8))预测极限弹速略低于相应弹速模型(式(5)与式(7))预测结果，且由弹坑深度模型(式(5)与式(6))预测极限弹速略低于背凸高度模型(式(7)与式(8))计算结果。综合考虑模型拟合精度与最大弹坑深度和背凸高度仿真计算中存在的误差，推测该靶材弹击失效的极限弹速应在1000 m/s附近。

2.3 预测模型修正与预测精度

由于本仿真未考虑靶材残余应力的影响，同时假定材料力学性能均匀，很明显这与实际存在一定差异，且残余应力会影响材料的失效行为[13,14]，因此需用测试结果对以上预测数学模型进行修正。如上讨论，从弹速出发，射距为40 m时的弹击条件与仿真计算中825 m/s的瞬时接触弹速条件可近似认为相同，故可采用40 m打靶实测结果对以上预测数学模型进行修正，修正后模型分别如式(9)至式(12)所示。

H=-9.575+0.01644v

(9)

H=-3.213+1.05988×10-5v2

(10)

D=-13.425+0.02372v

(11)

D=-4.247+1.52939×10-5v2

(12)

据实际打靶测试经验，子弹每飞行10 m则相应弹速约下降10 m/s。据此可近似计算出射距分别为50 m、60 m、70 m和80 m时的弹速，同时结合以上修正预测模型(式(9)与式(12))，即可计算出相应射距下的弹坑深度与背凸高度，如表4所示。由表中可以看出，由于在本研究考察弹速区间内抗弹参数D和H与弹速v和弹速平方v2均保持良好线性正比关系，故由v模型和v2模型计算所得预测结果基本相同。与此同时，除射距为60 m的背凸H和孔深D外(两者均高于40 m射距时的相应值，这与理论不符，可能为测试误差或靶材性能不均所致)，修正后的数学模型预测精度均可达92%以上。

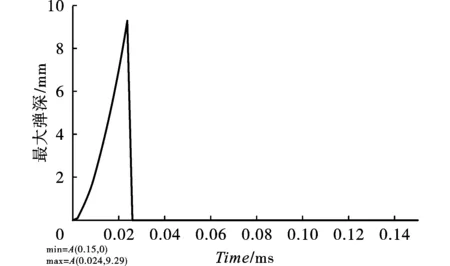
图 9 弹坑深度变化曲线Fig. 9 Curve of crater depth

图 10 背凸高度变化曲线Fig. 10 Curve of back bulge height

表 4 不同射距下靶材抗弹性实测与修正模型预测对比

3 结论

本文通过数值计算和试验研究，对弹击下薄基体装甲钢的侵彻行为进行了研究，并对该靶材弹击失效的极限弹速进行了预测。综合试验与仿真结果，得到的主要结论如下：

(2)弹击仿真过程总质量最大变化率为2.3%，沙漏能亦仅占总能量的2.7%，均满足低于5%的要求，表明所建立弹击仿真有限元模型有效可信，弹坑深度与背凸高度计算结果与实际打靶测试结果吻合度较高，其仿真计算精度分别为86.5%与88.2%。

(3)依据仿真结果，该靶材弹击失效的极限弹速预计为1000 m/s左右，在所考察弹速范围内，修正后靶材弹坑深度与背凸高度受弹速与弹速平方影响的数学预测模型分别为D=-13.425+0.02372v，D=-4.247+1.52939×10-5v2，H=-9.575+0.01644v和H=-3.213+1.05988×10-5v2，且其预测精度均达92%以上。