基于船形焊的双机协作路径规划

李俊渊，廖伟东， 高燕，黄昕，邓华健

(国机智能科技有限公司，广东广州 510535)

0 前言

随着“中国制造2025”计划的推进，工业生产制造中机器人焊接逐渐替代了人工焊接，但是大多数焊接路径仍是通过示教生成。但是示教编程需要操作者耗费大量时间，而且示教的路径精度得不到保证，因此难以保障焊接质量和生产效率。

大量实践证明，焊接点以船形焊接姿态，即焊接点的切矢量呈水平方向、法矢量呈重力的相反方向时，可以获得良好的焊接质量和较高的焊接速度。然而，生产制造中要求焊接的工件越发复杂，仅依靠示教编程难以控制机器人在焊接过程始终保持船形焊姿态，焊接质量难以得到保障。因此，机器人焊接路径规划不仅要考虑焊接工艺，而且要考虑机器人本身的运动性能，这样才能在更好地提高机器人焊接速度的同时获得较好的焊接质量。

本文作者以船形焊为目标，建立船形焊接算法模型，设计在焊枪姿态约束下的机器人运动平稳性能评估指标，并作为评价焊接目标函数。利用灰狼优化算法对协作焊接路径进行目标寻优，使得焊缝中所有焊接点处于最优的船形焊接位姿，焊枪处于理想焊接姿态，实现机器人与变位机通过协作进行船形焊接的路径优化。本文作者在一台六轴串联机器人及配套二轴变位机系统的基础上进行研究，系统模型如图1所示。

图1 焊接机器人系统

1 性能指标函数及其分析

为实现控制机器人在焊接过程始终保持船形焊姿态，在提高机器人焊接速度的同时获得较好的焊接质量，本文作者建立船形焊接算法模型、机器人平稳性能指标函数以及焊枪姿态约束条件，以评价系统的运动性能。

1.1 船形焊接算法

待焊工件固定在变位机的转盘上，变位机各个关节转动之后，焊缝上各个待焊点的空间位姿可以通过变位机的正运动学变换得到。而待焊点的空间位姿需要满足船形焊接工艺要求，则需要对变位机进行逆运动学分析得到变位机各个关节的角度。为此，在变位机每个关节连杆分别建立如图2所示的坐标系。其中，{}为变位机的基坐标系；{}为变位机末端转盘的坐标系，与连杆2的固有坐标系{2}相同；连杆1的固有坐标系{1}与{}、{}原点重合。

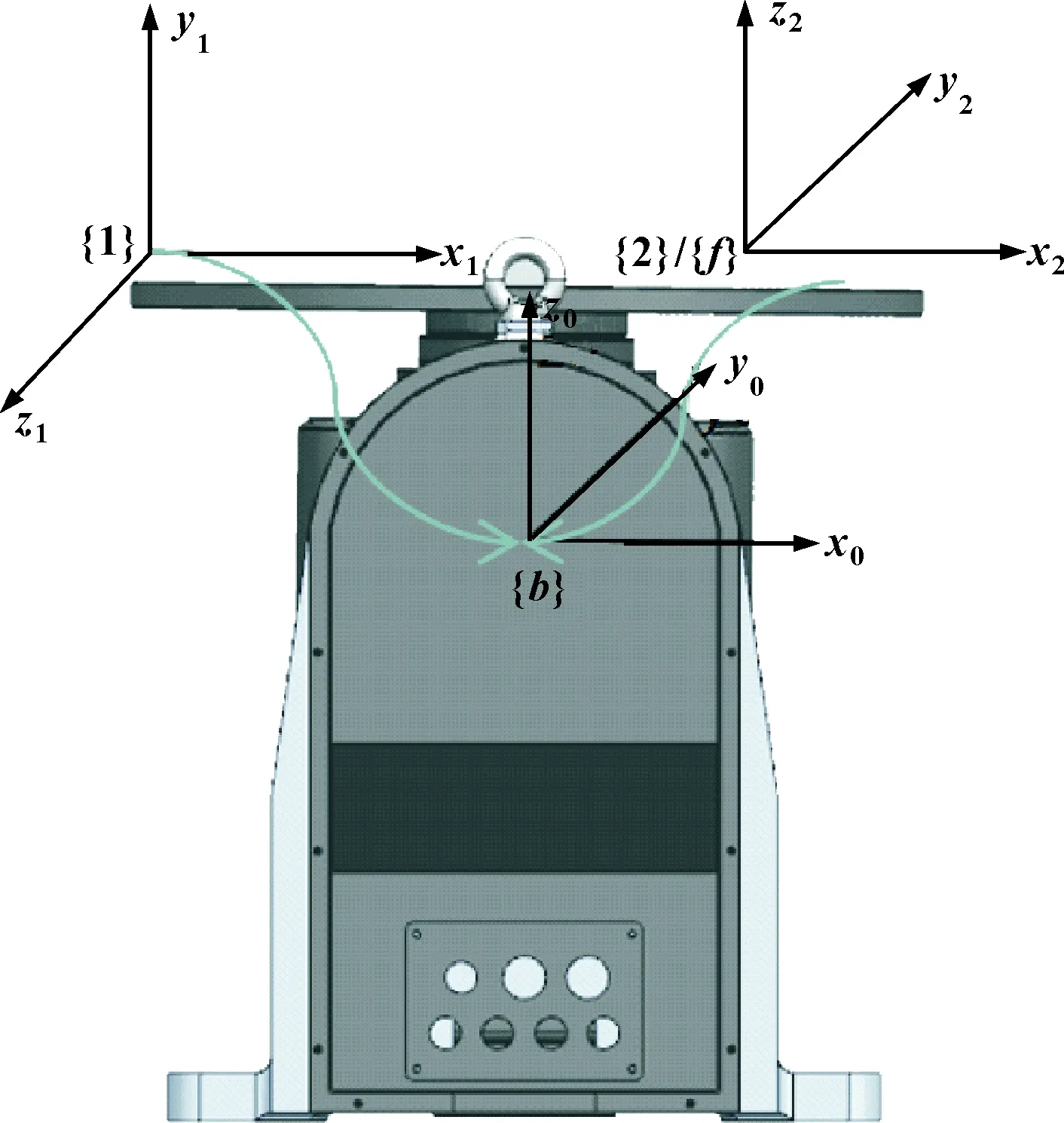
图2 变位机的坐标系

变位机的连杆参数如表1所示。

表1 变位机连杆参数

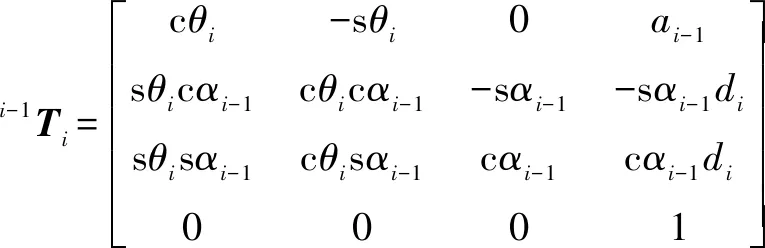
(1)

根据式(1)，可以求出连杆变换矩阵、，将它们连乘得:

=

(2)

(3)

焊接点坐标系{}相对于变位机基坐标系{}的位姿变换由机器人运动学得到：

=

(4)

(5)

焊接点坐标系{}的法向量应具有竖直向下的特点，即：

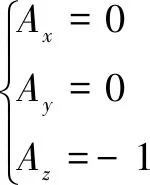
(6)

联立式(4)—(6)可得，满足船形焊接要求下变位机的关节角1、2分别为

2=arctan2(-,)

(7)

1=arctan2(cos2-sin2,)

(8)

在双机器人协调焊接系统中，机器人的基坐标系为{}、机器人的法兰盘坐标系为{}、焊枪坐标系为{}，则根据机器人运动学可得：

=

(9)

=

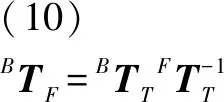
(11)

由式(9)—(11)计算得到后，根据机器人的逆运动学，可以计算得到机器人各个关节角。

1.2 运动平稳性能指标函数

为得到良好的焊接质量，需要综合考虑在焊枪姿态约束下机器人运动平稳性指标。焊接过程中机器人各关节运动的变化过程越平稳、焊枪不抖动，机器人的定位误差就越小。因此，机器人经过所有焊接点时的关节变化量可以用来表示机器人运动平稳性能。由于机器人各关节变化量对系统的运动平稳性影响各不相同，采用加权的方法来表示。机器人运动平稳性能指标函数可描述为

(12)

其中：为机器人的关节角；为考虑机器人各关节惯量所取的权值；=1时,机器人的初始状态角为、、、、、。

1.3 焊枪姿态约束

焊枪的姿态一般用、和来表示，焊枪工作角和行走角对焊接质量影响较大，而自转角对焊接质量没有影响。对于空间位姿已确定的焊缝，理论上，焊枪存在一个最优的焊接姿态。当机器人把持焊枪以最优姿态焊接时，能获得最佳的焊缝成形质量。然而，由于焊接过程中可能经过奇异点、轴限位或不可达区域等情况，为保证运动的合理性，一般将焊枪姿态在一定范围内作微小调整。当姿态偏差不大时仍然能够保障较好的焊接质量。因此，对焊枪工作角、行走角及自转角与最佳的焊枪姿态角的偏差值进行约束：

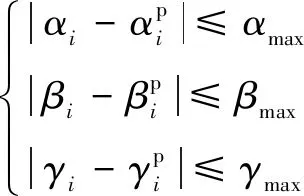
(13)

2 灰狼优化算法

灰狼优化(Grey Wolf Optimizer,GWO)算法模拟自然界中灰狼的捕食猎物行为，是一种新的群体智能优化算法，以其简单、参数少、搜索能力较强等特点受到许多研究者的青睐。GWO算法优化过程包含了灰狼的社会等级分层、跟踪、包围和攻击猎物等步骤。采用GWO算法对协作焊接路径进行目标寻优，就是使机器人经过个焊缝点的位姿时，其运动过程平稳，焊枪姿态相比于理想姿态偏差不大时仍然能够获得相对良好的焊缝成形质量。因此，本文作者取运动平稳性函数作为灰狼算法的适应度函数。灰狼算法的优化对象：

=[Δ,Δ,Δ,Δ,Δ,Δ,…,Δ,Δ,Δ]

(14)

其中：

(15)

式中：Δ、Δ和Δ分别表示第个焊缝点的焊枪工作角、行走角及自转角与最佳的焊枪姿态角的偏差。式(13)作为优化对象的约束条件。

位姿变换矩阵中，焊枪坐标系{}相对于理想焊接点{}的姿态变换矩阵采用--欧拉角表示，即：

(16)

焊枪坐标系{}相对于理想焊接点{}的位置不变,由此可以确定值。

基于GWO算法的焊接机器人最优路径规划的基本流程如图3所示。

图3 基于GWO算法的焊接机器人最优路径规划流程

3 协调路径规划实验

实验工件采用直径150 mm的圆形钢管垂直相交于直径100 mm 的圆形钢管，交线即为焊缝。对焊缝进行24等分，即=24，得到24个焊接点{}，理想焊接点处于船形焊位姿，即理想焊接点的切向量沿水平方向，而法向量与重力的方向相反。由船形焊接算法可以得到满足船形焊接要求的变位机的关节角变化如图4所示。

设机器人的初始状态为=0、=90°、=0、=0、=0、=0。焊枪工作角、行走角和自转角允许的最大变动值===0.1°；通过示教器工具标定操作测得工具坐标系=[0.930, 0.000,-0.368,79.806;-0.028,0.997,-0.070,-8.571;0.367 0,0.075,0.923,432.517;0.000,0.000,0.000,1.000];通过示教器变位机标定操作测得=[1.000, 0.000,0.000,931.511;0.000,1.000,0.000,-31.988;0.000,0.000,1.000,-52.153;0.000,0.000,0.000,1.000]。取灰狼数为50，最大迭代次数=100；按照如图3所示的流程执行路径规划后，适应度函数值=18.469 8，如图5所示。机器人与变位机协作焊接路径规划结果分别如图6和图7所示，仿真如图8所示。可以看出：利用该方法可以有效地规划出机器人与变位机各个轴运动平滑、合理的轨迹，焊枪工作角、行走角和自转角均在 ±2×10rad内以较小幅度变化。实际焊接后可以获得较好的焊接质量。

图4 变位机的关节角变化过程 图5 适应度函数随迭代次数的变化过程

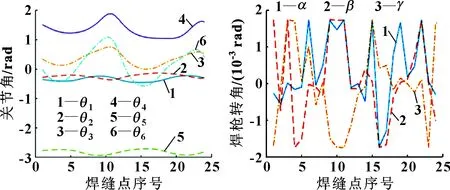
图6 机器人各关节角的变化过程 图7 焊枪姿态的变化过程

图8 路径规划结果的仿真

4 结论

为达到船形焊接的目标，对变位机运动学进行了分析，建立了船形焊接算法模型；提出了考虑焊枪姿态约束下的机器人运动平稳性能指标函数，并以此作为优化目标函数，利用灰狼优化算法对协作焊接路径进行目标寻优；使得焊缝中所有焊接点处于最优的船形焊接位姿，焊枪处于理想焊接姿态。在整个焊接过程中，机器人与变位机的轨迹都十分平滑，有效地保障了焊接的质量并提高了生产效率。