精密加工中心直线轴复合误差建模研究

2022-09-19赵南皓齐向阳熊明辉黄平钰郭政

机床与液压 2022年16期

赵南皓，齐向阳，熊明辉，黄平钰，郭政

(1.天津工业大学机械工程学院，天津 300387；2.沧州市农机推广站，河北沧州 061000)

0 前言

当前，我国制造业正处于高速发展阶段，对工件的加工更加追求高精度、高效率、高智能。然而，在实际加工过程中总伴随着各种误差，从而影响机床加工精度。研究显示：在诸多误差项中，几何误差和热误差就占据所有误差的50%以上。所以，在机床误差的研究中，建立几何与热误差的复合模型对提高机床精度尤为重要。高精度工件的加工依赖于精密机床，而大型、重型、高精度机床的直线轴常采用两端固定的安装方式，丝杠两端都受约束限制，其热误差产生机制与固定-自由、固定-支撑的安装方式并不相同，因此对具有两端固定安装方式的丝杠进给系统进行研究具有重要意义。

近年来，为降低机床误差，国内外学者致力于误差建模技术的研究，从静态几何误差建模发展到热误差建模，以及两种误差的复合建模技术。静态几何误差是机床本身固有的误差，其建模方法常采用拟合法和插值法。拟合法建模方式多采用最小二乘法、多项式参数化建模法；插值方法常采用牛顿插值、三次样条插值、B样条插值。其中切比雪夫多项式参数化建模方法具有建模简单、易程序化的特点，用于几何误差建模具有更高的精度。

机床热误差，是在机床运行过程中，由于丝杠螺母副的摩擦热、丝杠两端轴承摩擦热以及电机等多处热源的影响导致机床温度分布发生变化，由此机床零部件会发生热变形而产生热误差。对热误差预测，常用的两类建模方法是数据驱动法和模型驱动法。数据驱动法是将测得的温度作为模型输入，将热误差作为输出，将实验获得的数据集用于训练模型。学者们多使用神经网络、多元线性回归和状态空间等方法建立热误差模型。模型驱动法是对热特性机制进行分析，计算生热量和边界条件作为模型输入量，将温度或热误差作为输出。常用方法为有限元法和有限差分法。这类研究方法可降低实验成本，避免实验所带来的繁琐性。

由于机床存在多类误差，如果只对单类误差建立模型，可能会适得其反。因此，建立复合误差模型至关重要。几何与热致定位误差主要受滚珠丝杠的制造精度以及热变形影响。本文作者针对卧式精密加工中心对几何与热致定位误差进行研究，在考虑两端约束情况下分析丝杠的临界载荷与热应力的关系，建立热误差模型。对几何定位误差建模采用切比雪夫多项式方法，利用多光束激光干涉仪XM-60检测机床直线轴在不同时刻的误差，实时采集关键点温度，最终将复合模型与实验结果对比，结果表明：复合模型具有较高的预测精度。

1 丝杠进给系统热误差机制分析

机床直线轴的温度变化受多种因素影响，这些因素都会使丝杠温度发生变化从而产生热变形。如图1所示，两端固定式丝杠进给系统产生热变形时，在轴承刚度影响下，其丝杠两端均受到轴向径向载荷，限制丝杠热膨胀，从而起到降低热误差的效果。

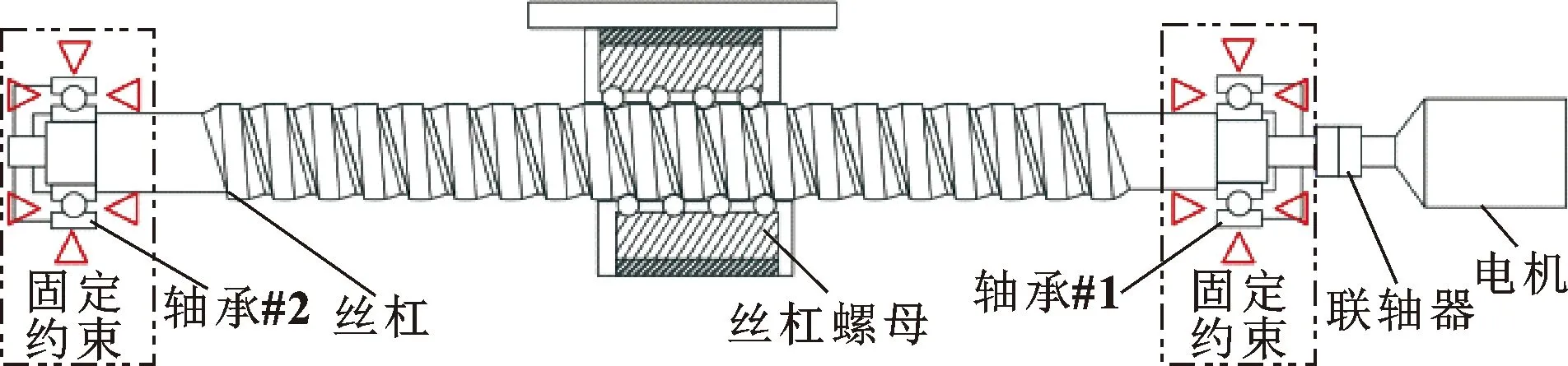
图1 两端固定式丝杠

在丝杠受热变性前，会有一个初始的轴向预载荷来限制丝杠的热膨胀，随着机床运行，丝杠内部热应力不断增大。当丝杠内部热应力未达到临界载荷时，丝杠会处于水平状态，相对轴向位移为零；当超过临界载荷时会发生挠曲变形，如图2所示。因此热应力产生的变形量是临界载荷所限制的轴向变形量与挠曲变形产生的轴向误差之和。

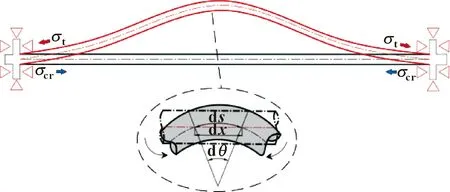
图2 丝杠挠曲变形

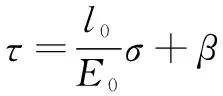
(1)

式中：为预载应力，Pa；为丝杠初始长度，m;为弹性模量，N/m；为挠曲变形引起的轴向伸长，m。

在丝杠冷态条件下，取丝杠微元长度d，当丝杠发生热膨胀时，由于受到两端约束的限制，此时发生挠曲变形，其初始微元长度变为d，此时丝杠伸长率为

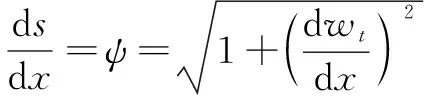
(2)

在两端紧固状态下，丝杠发生挠曲变形后引起的轴向伸长为

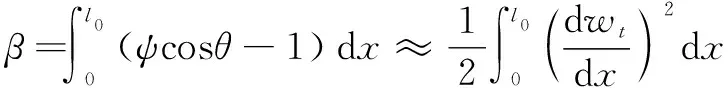
(3)

式中：为挠曲线切线与水平方向夹角；为挠度误差。

在考虑没有约束情况下时，由温度引起的丝杠轴向伸长量为

(4)

式中：为热膨胀系数，10m/℃；Δ(,)为丝杠表面温升量，℃；为热应力，Pa。

将式(2)(3)代入式(1)得：

(5)

挠曲线微分方程通解以及丝杠两端边界条件为

=cos+sin++

(6)

(7)

式中：、、、为未知系数；为挠度波长系数。将边界条件(7)代入(6)，解得挠曲线方程为

=sin

(8)

将式(6)代入式(4)解得：

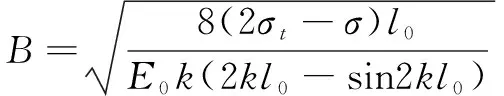
(9)

式中：=π/，为长度因数，这里假设丝杠实际伸长量全变为挠曲变形，取=2。根据挠度与轴向位移的关系，推导出轴向热位移误差为

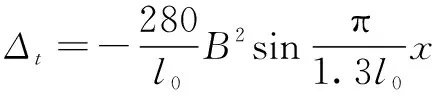
(10)

丝杠在受热载荷的条件下产生热应力，热应力会使丝杠产生挠曲变形，通过挠曲线方程推导，将式(9)代入式(10)，得到热误差表达式。这里设丝杠的热误差的幅值=-280，波长=π/1.3；比较热应力与临界应力之间的关系，得到两端固定式丝杠进给系统热致定位误差模型：

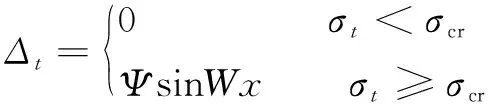
(11)

由推导公式可得：当机床工作时，丝杠热应力会逐渐增加，当热应力小于临界应力时，即<,其轴向热位移为零，这说明两端固定式丝杠进给系统对热误差具有一定的限制;当丝杠温度达到一定值时，热应力将大于临界应力，即≥，得到的热误差模型是以丝杠升温与位移为自变量的正弦函数表达式。这为两端固定式丝杠进给系统热误差建模与补偿提供了基本思路。

2 几何误差与热误差复合建模

2.1 基于有限元法瞬态热仿真分析

丝杠表面在多处边界条件影响下，想要通过理论计算解出温度模型非常困难。本文作者基于有限元法来提取丝杠表面温度场,因此对空心丝杠进给系统建立生热、散热计算模型。

(1)轴承生热计算

滚动轴承的生热主要由滚动体与套圈之间摩擦力矩以及润滑剂的流体动力学损耗所引起的，其生热率计算公式为

=0104 7

(12)

(13)

式中：为轴承转速，r/min；为轴承摩擦力矩，N·m；为与轴承类型、转速和润滑剂性质有关的力矩；为与轴承所受载荷有关的摩擦力矩。

(2)丝杠生热计算

丝杠螺母副是由滚珠与滚道间摩擦产生热量，其生热计算公式与轴承生热计算相同。丝杠螺母摩擦力矩为

=094+

(14)

式中：为预紧阻力矩；为驱动力矩。

(3)电机生热计算

电机与丝杠前轴承处一端通过联轴器连接，其温度不会直接影响丝杠，但电机的生热会影响前轴承座的温度，因此需计算电机生热量。其计算公式为

(15)

式中：为电机输出扭矩；为电机机械效率。

(4)对流换热系数

(16)

式中：为努赛尔数；为空气热传导系数；为特征尺寸。

(5)空心丝杠冷却液强制散热

=(-)

(17)

式中：为冷却液密度，kg/m；为冷却液流量，L/min；为冷却液比热容，J/(kg·℃)。

2.2 建立丝杠温度模型

所研究的卧式精密加工中心采用的是双驱动进给系统，对滚珠丝杠进给系统单元的各部分材料物性参数进行定义，如表1所示。

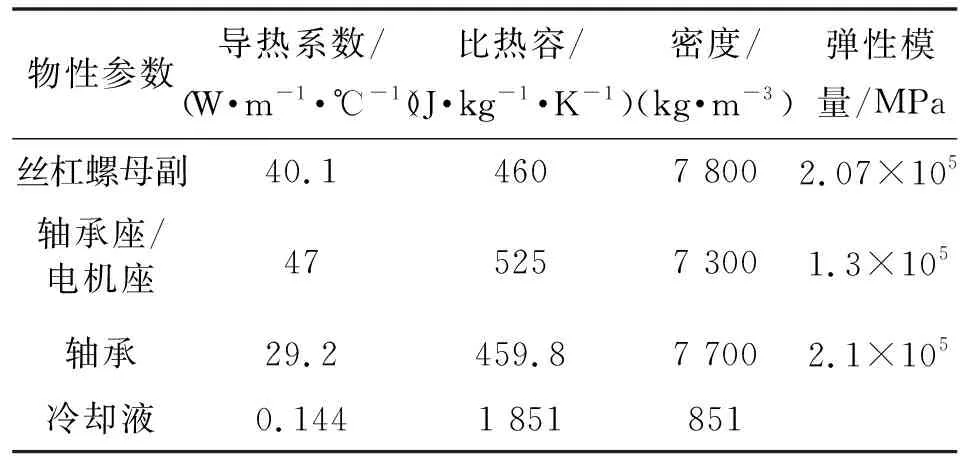
表1 丝杠螺母副各部分物性参数

图3为向进给系统，首先利用ANSYS Fluent进行流体分析获得冷却液出口温度，计算出冷却液进出口温差为0.69 ℃；以工况为15 m/min的进给速度对向丝杠进给系统进行瞬态热分析。设置环境温度为20 ℃，根据上述经验公式计算出热载荷以及边界条件参数，如表2所示。

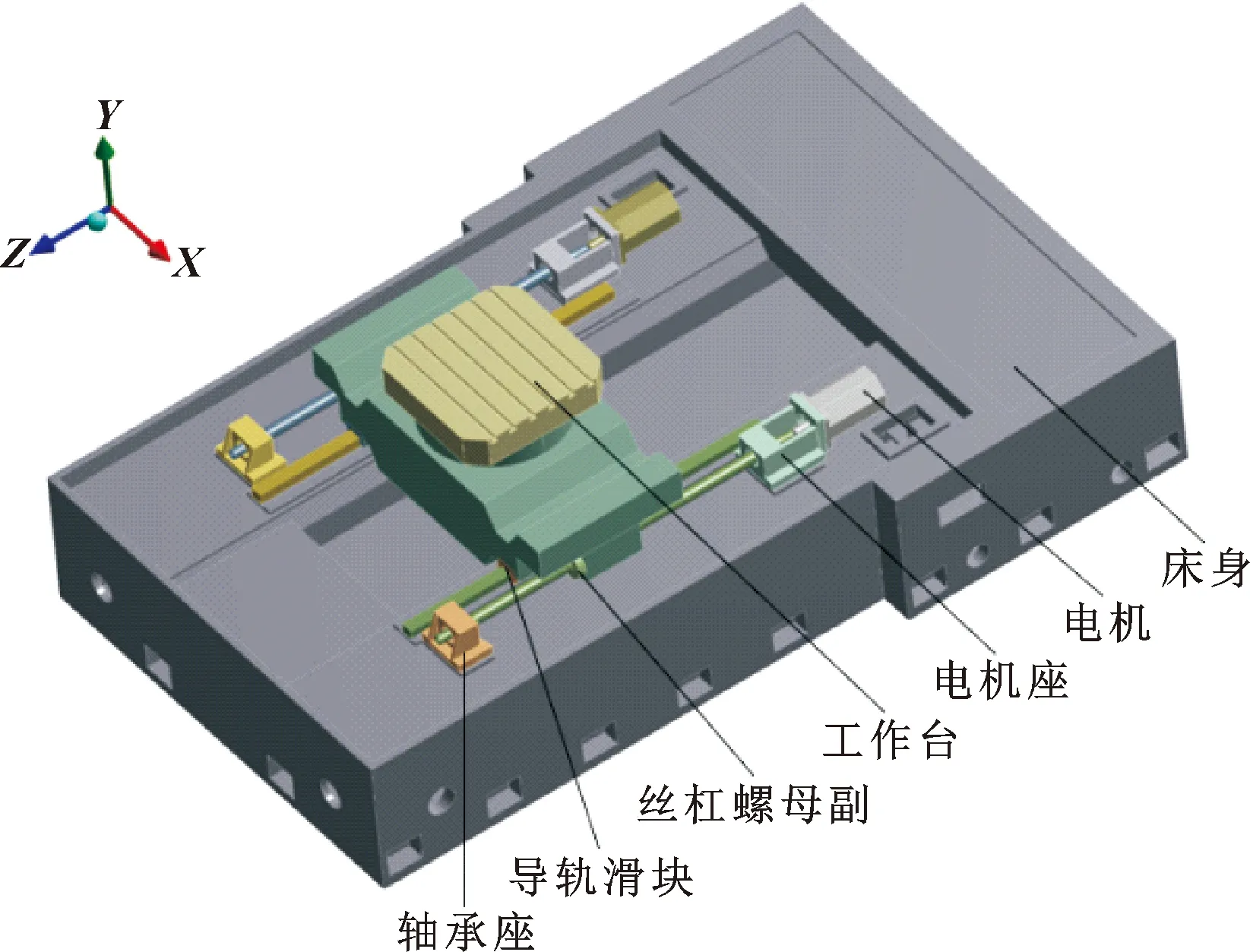
图3 Z向进给系统

表2 各部位热载荷与边界条件

设置丝杠螺母运动行程为900 mm，利用imprint faces生成有效路径面，对有效路径施加丝杠螺母副摩擦产生的热流密度。根据经验，精密加工中心达到热平衡时间约为14 400 s，为验证热平衡时间的准确性，故取18 000 s为滚珠丝杠螺母副的总仿真时间。设置最小载荷步为18 s，最大载荷步为600 s。将上述参数施加到有限元模型中，计算得到向滚珠丝杠进给系统温度场。

对双驱动丝杠进给系统两边施加同等边界条件，其热源分布较为对称，以右丝杠进给系统为例，仿真结果如图4所示。

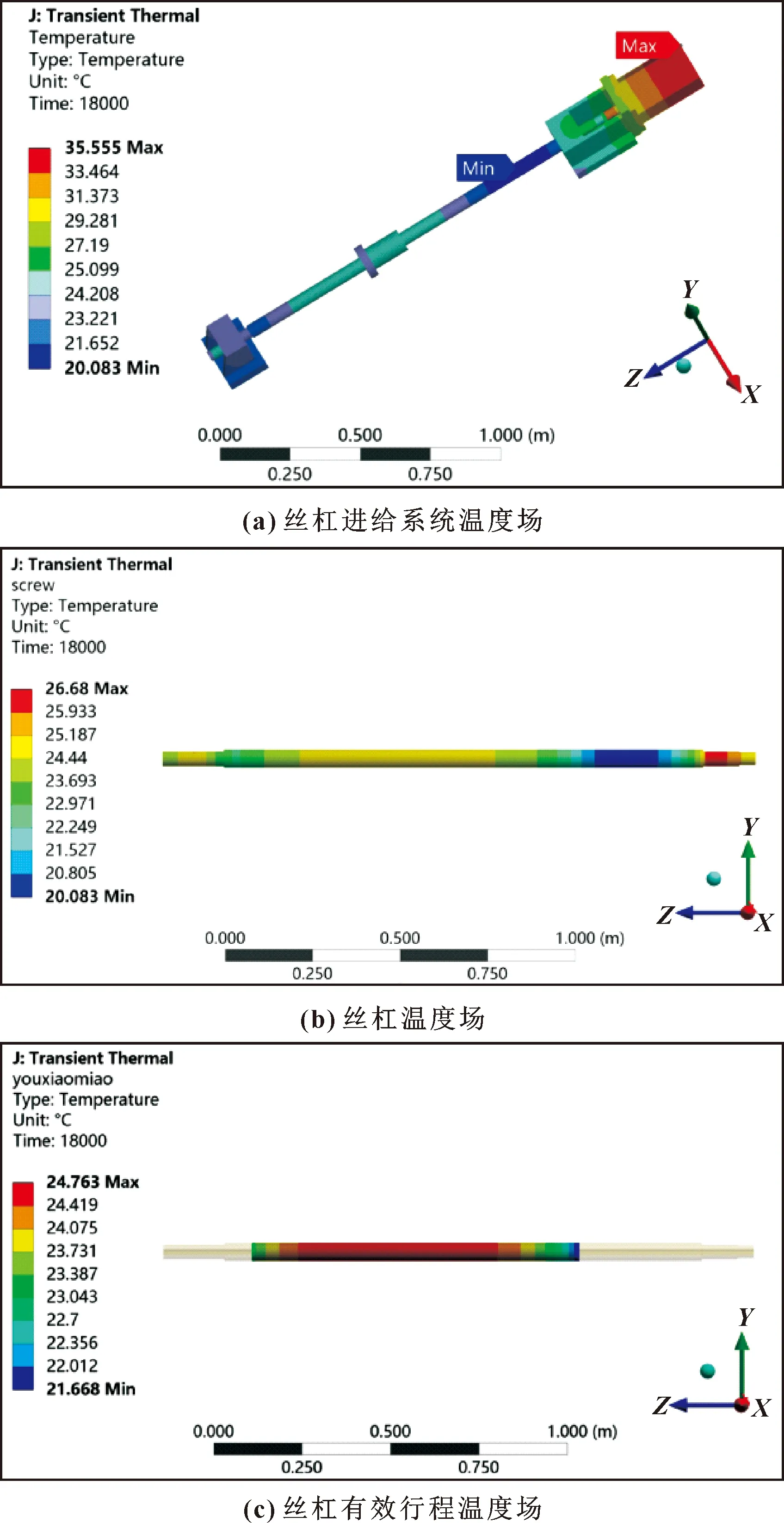
图4 有效行程下丝杠表面温度

由图4(a)可知:前轴承座温度高于后轴承，是由于电机温度的影响，但丝杠靠近前轴承部分温度较低是由于选取的有效行程偏向于后轴承，因此丝杠在靠近前轴承处没有产生摩擦热。提取丝杠有效行程下的表面温度，将丝杠表面温度数据导入到MATLAB中,在有效行程下丝杠表面温度如图5所示。

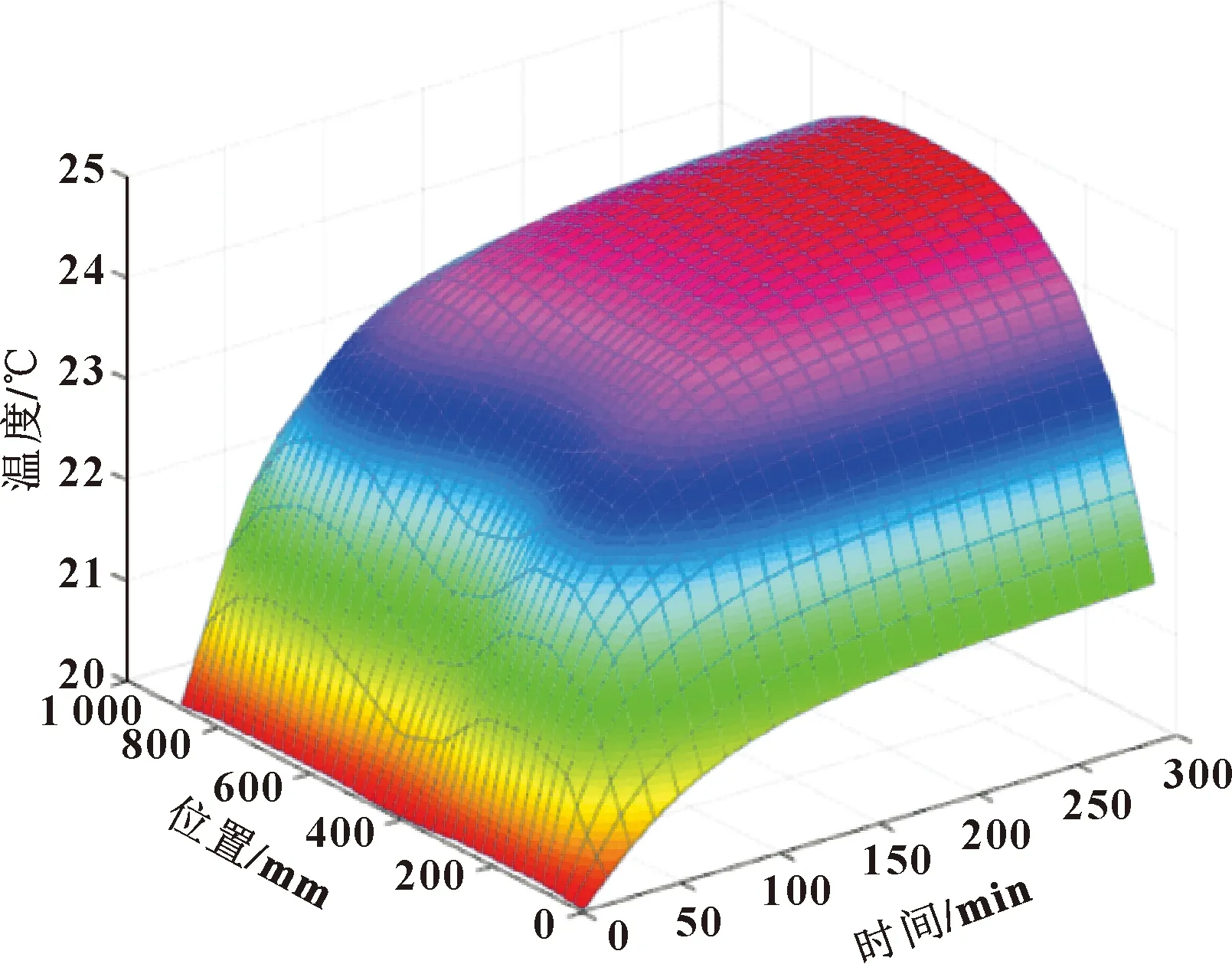
图5 有效行程下丝杠表面温度

利用MATLAB将丝杠瞬态温度代入到式(4)，其中丝杠热膨胀系数=1.18×10℃，计算热应力变化情况，取位置270、540、810 mm处的丝杠热应力的变化情况如图6所示。临界预载荷为最大工作载荷的1.35倍，故临界应力值=4.88 MPa。由图6可发现3个位置在非稳态条件下均大于临界应力值，在4 h左右达到稳态状态，且在1 h内负载热应力增长幅度最大，即在=1 h时产生的热变形量较大。

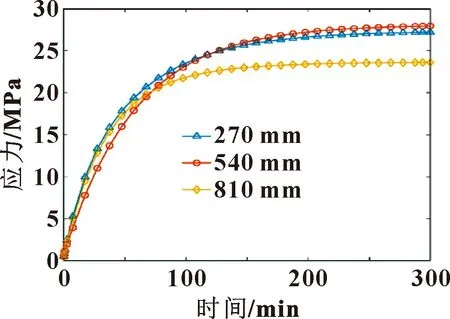
图6 丝杠热应力

将丝杠表面温度数据进行统一化处理，除去波动较大的温度数据，计算每小时丝杠表面平均升温量，将丝杠表面升温量代入到式(9)中计算得到热误差幅值，见表3。根据式(11)计算在1、2、3、4 h时刻的热致定位误差如图7所示。

表3 不同时刻丝杠表面升温值与幅值

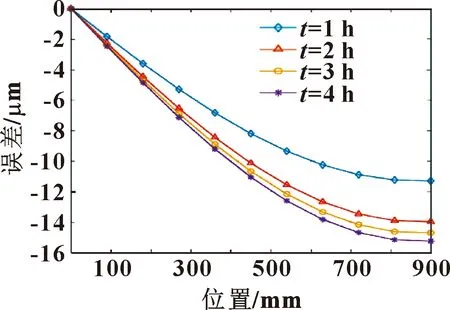
图7 热误差

2.3 基于切比雪夫多项式几何误差建模

在机床运行零时刻所产生的误差视为几何误差，由于几何误差受到加工与装配等诸多影响因素，因此对其理论计算较为困难，本文作者采用切比雪夫多项式对几何定位误差进行参数化建模。

切比雪夫多项式是以递归方式所定义的一系列正交多项式，第一类切比雪夫多项式在多项式插值时可最大限度降低龙格现象，可实现连续函数的最佳逼近。第一类切比雪夫前4项公式为

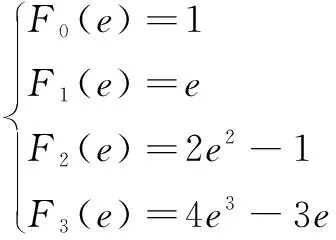
(18)

式中：为切比雪夫变量。

对直线轴运动行程进行归一化处理，其转换关系为

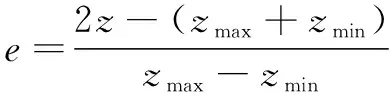
(19)

式中：为行程最大值，=900 mm；为初始位置，=0 mm；建立切比雪夫多项式模型并计算基函数的回归系数：

=()+()+()+…+

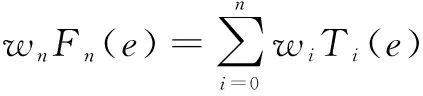
(20)

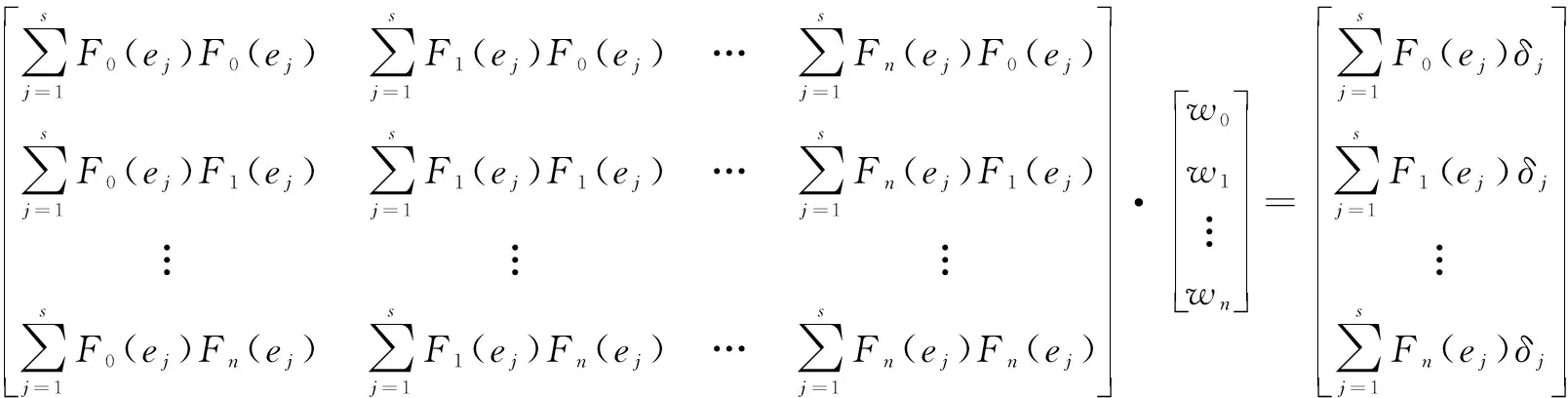
(21)

式中：为回归模型；为数据点个数；为第个检测数据；为误差数据；()为阶切比雪夫多项式。

根据式(21)计算得到回归系数，并代入到式(20)中，解得含有切比雪夫变量的多项式，再将式(18)代入，得到最终的直线轴静态下的几何定位误差模型为

(,0)=-6993 9-5226 3+0939 7(2-1)-1052 8(4-3)

(22)

将几何误差与热误差模型叠加如式(23)，得到向直线轴几何与热误差复合模型。

=(,0)+(,)

(23)

3 复合误差模型实验验证

为验证复合定位误差模型的正确性，在JIG630精密卧式加工中心上进行复合定位误差检测实验。通过测得不同时刻下的定位误差来验证所建立模型的正确性。

3.1 实验设计

以精密卧式加工中心的向进给系统为研究对象，利用多束激光干涉仪XM-60作为定位误差检测装置,在螺母座、前轴承座、后轴承座、电机、冷却液进出口处布置温度传感器，对关键点温度进行实时检测，布置方式如图8所示。

图8 精密机床实验平台

复合定位误差检测流程：在初始冷态下，采用XM-60对机床轴几何定位误差进行测量，然后以进给速度为15 m/min进行往复运动，每隔1 h对轴进行一次定位误差测量，当运行4 h左右时，温度基本达到稳态，进行最后一次测量。除初始冷态测得的为几何误差，其余4次误差测量，均为几何与热的复合定位误差。

3.2 实验结果与分析

以进给速度15 m/min运行的向丝杠进给系统各关键点温度与仿真温度对比如图9所示，实验过程中环境温度为(20±0.5)℃，冷却液流量为5 L/min，整个实验过程保持不变。

如图9所示:随着机床运行时间的增加，关键点温度不断增加，电机座相对于轴承座温度较高，是由于电机的生热对电机座有一定的影响。第一个小时增加幅度最大，随后生热减少，实验温度呈波动趋势，是由于每次定位误差检测，丝杠停止运行，机床处于自然散热，会出现降温的趋势。

图9 温度仿真实验对比

仿真结果与实验温度曲线进行对比，各关键点瞬态仿真曲线的升温趋势与实验温度曲线相符，且达到稳态时的仿真值与实验值相差不大，丝杠表面温度受各处关键点温度的影响，证明利用有限元法对丝杠表面温度进行描述具有正确性。

对机床向进给系统每隔1 h进行误差检测，测量行程与仿真行程保持一致，每次测量得到几何误差与热误差的复合定位误差，机床运行1 h后产生的热致误差最大，2 h之后误差幅度增加变小，是由于丝杠表面温度在1 h左右增幅最大，2 h之后升温幅度变得缓慢，当运行4 h左右时，温度基本达到稳态，所以将4 h后的误差作为稳态误差。将几何误差与不同时刻下的热误差代入式(23)，得到不同时刻几何与热复合误差模型。实验曲线与预测曲线进行对比，如图10所示。

图10 不同时刻下复合误差实验值与预测值

由图10可看出:机床冷态状况下预测值与测量值最大误差为1.42 μm，机床跑车1 h，复合误差预测值与测量值最大误差为0.92 μm；跑车2 h，复合误差的预测值与测量值的最大误差为1.285 μm；跑车3 h，复合误差的预测值与测量值的最大误差为1.285 μm；跑车4 h，复合误差的预测值与测量值的最大误差为1.85 μm。复合预测精度达到85%以上,验证了几何与热误差复合模型的有效性。此外，对于两端固定式丝杠进给系统，预测模型计算得到的热致误差小于实测值，其原因是由于床身在多处热源的影响下会发生变形，从而会减少两端的临界载荷对丝杠的限制，进一步增大热致定位误差的产生。