一种滑动聚束SAR子孔径成像算法
2019-12-04陈家瑞
赵 莉,陈家瑞,柏 磊
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
合成孔径雷达(SAR)成像技术经过多年发展,已经具有多种不同的工作模式,如:聚束模式、条带模式、扫描模式、滑动聚束模式等,其中,滑动聚束模式是一种介于聚束和条带之间的模式,该模式中通过不断调整天线波束中心指向,使其始终指向场景远处一个虚拟旋转点,当雷达平台沿着航迹飞行,波束在地面扫出一条扫描带得到回波数据,从而实现对场景SAR成像。为了在高分辨率滑动聚束模式基础上尽可能实现大的成像场景,需要更长的合成孔径长度,获得更大的方位向带宽,在脉冲重复频率(PRF)一定的条件下增加方位带宽容易出现方位频率混叠问题,影响后续SAR成像处理[1-2]。目前处理该问题主要有2类算法:“两步法”[1-3]和子孔径类算法[4-5]。“两步法”在成像算法之前对数据进行预处理消除方位频谱混叠,但是会对整个成像处理增加计算量,影响处理效率。子孔径类算法是将合成孔径划分为N(N≥2)个子孔径进行子孔径成像处理,然后将子孔径图像通过数据拼接得到SAR图像。子孔径方法增加的计算量少,对资源要求低,灵活性大。
本文首先介绍了滑动聚束SAR成像模型,提出基于ωK算法的子孔径成像算法,解决滑动聚束SAR成像处理中的方位频谱混叠问题,并通过仿真处理,验证了该子孔径成像算法的可行性和有效性。
1 滑动聚束SAR几何模型
1.1 滑动聚束模型
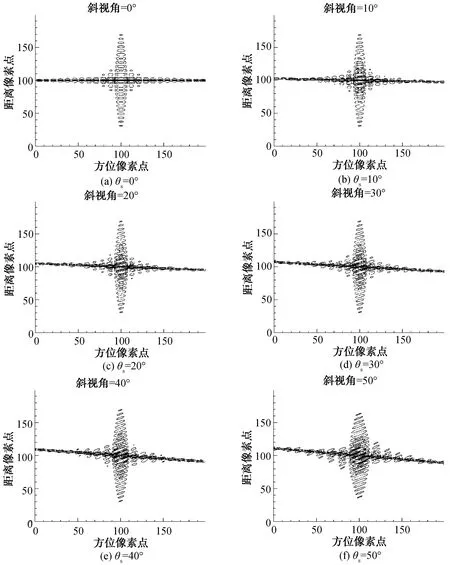
机载滑动聚束SAR成像斜平面模型如图1所示。载机速度为Va,O为孔径中心,O′为场景中心点,波束中心在地面扫描速度为Vg(Vg 图1 滑动聚束SAR斜平面几何模型 在进行滑动聚束扫描时,载机从A点飞往B点,波束中心在地面从A′点扫描到B′点。场景中目标点P距雷达的瞬时位置X的距离为R(ta;RP): (1) 雷达发射的信号为: (2) 式中:rect(·)为矩形窗函数;fc为载频;Kr为LFM信号的调频斜率;Tr为脉冲宽度;τ为快时间;Ta为合成孔径时间,Ta=Tend-Tstart。 当波束能照射到P点时,发射的LFM信号经过2倍的R(ta;RP)延时,得到回波信号,然后去载频解调后得: s(τ,ta;RP)= exp(-j2πfcΔτ)exp[jπKr(τ-Δτ)2] (3) 式中:Ls为波束照射到地面的方位向宽度;σn为目标的雷达截面反射系数;Δτ为目标点P回波双程延时: (4) 基于ωK算法的子孔径法是将全孔径划分为子孔径,每一个子孔径经过ωK算法成像处理,在子孔径的划分过程中消除了方位频谱混叠,随后将子孔径图像数据进行拼接,得到全孔径SAR图像。对于景中任意点P第i个子孔径(共划分成N个子孔径)回波信号可以写成: exp(-j2πfcΔτ)exp [jπKr(τ-Δτ)2] (5) 式中:Tsub为子孔径长度。 对第i个子孔径经过ωK算法处理得到二维频域表达式: (6) 利用子孔径数据中带有不同方位的位置信息,才能实现子孔径图像数据拼接成全孔径SAR图像。 子孔径数据经过ωK算法处理后,消除了距离徙动以及实现了方位向聚焦,子孔径数据拼接需要在数据域拼接,因此在拼接前,需将ωK算法处理后的数据恢复到方位调频信号,将ωK算法聚焦后的子孔径数据,在方位向乘以Scaling因子,将子孔径数据恢复为已知的线性调频信号,Scaling因子为: (7) 为实现数据域子孔径拼接,恢复方位线性调频后的子孔径数据通过反快速傅里叶变换(IFFT)变为数字域,由于原数据每个子孔径方位中心频率不同,在拼接前,需将拼接数据的方位中心频率恢复到原数据频率上,因此需进行全孔径方位去旋转,方位去旋转因子为: Hde-rot=exp(jπKrotta_all2-j2πfdc_allta_all) (8) 式中:ta_all为全孔径方位时间;fa_all为全孔径方位频率。 方位去旋转处理后,进行方位快速傅里叶变换(FFT)以及方位脉压,方位脉压因子为: (9) 式中:Keff(r)=Krot-Kscl(r),脉压后进行方位向IFFT得到最终的SAR图像。 基于ωK算法的子孔径滑动聚束SAR成像算法处理流程如图2所示。图中的Roverlap为子孔径重叠率。 图2 子孔径算法处理流程 如图3(a)所示,在滑动聚束模式下,合成孔径时间ta持续越长,SAR回波信号方位带宽Ba就越大,将会超过方位采样频率,出现方位频谱混叠现象。基于ωK算法的滑动聚束子孔径成像算法,通过子孔径划分,使每个子孔径方位时间较全孔径时间ta有明显减少,从而降低了方位带宽,使其小于PRF,消除了方位频谱混叠现象。每个子孔径数据采用ωK算法完成成像聚焦后,为了后续子孔径拼接,还需将聚集后的子孔径数据恢复成方位调频形式,完成拼接后的方位频谱示意图如图3(b)所示。随后经过方位去旋转后,消除波束旋转调频,如图3(c)所示,其方位向带宽小于PRF,不会出现频谱混叠,由于此时方位向的宽带是由子孔径拼接前乘以调频因子恢复的,因此乘以该调频因子的频域的共轭,进行方位脉压便可完成成像。 图3 滑动聚束SAR子孔径处理方位频谱示意图 图4 点目标SAR成像仿真图 本实验雷达信号为线性调频(LFM)信号,采用X波段,载频fc=10 GHz,全孔径长度32 768个脉冲,划分为4个子孔径。定义孔径中心至虚拟旋转点连线与孔径法线的夹角为斜视角(如图1中θs),当θs=0°时为正侧视。为充分验证该子孔径算法,将分不同斜视角情况进行仿真实验,图4为采用基于ωK算法的子孔径方法处理的点目标仿真结果。 另外,图5计算了不同斜视角情况下,点目标方位向积分旁瓣比,对成像质量进行分析。 从图5(b)中可以看出,当斜视角θs=0°时,点目标方位向积分旁瓣比为-10 dB,当斜视角不断增大时,点目标方位向积分旁瓣比没有随斜视角的不同而恶化,基本保持在-10 dB附近,表明该子孔径算法在适用于不同斜视角情况下,均能保障SAR成像的图像质量,证明了机载滑动聚束SAR基于ωK算法的子孔径成像方法的有效性。 为了解决滑动聚束SAR模式下存在的方位频谱混叠问题,利用子孔径划分、子孔径成像与拼接的思想,本文提出了一种适用于滑动聚束模式下的子孔径成像算法。该方法解决了滑动聚束SAR大场景时方位频谱混叠问题,减少了硬件处理时间,点目标仿真实验验证了滑动聚束子孔径法的可行性和有效性。 图5 不同斜视角点目标方位向积分旁瓣比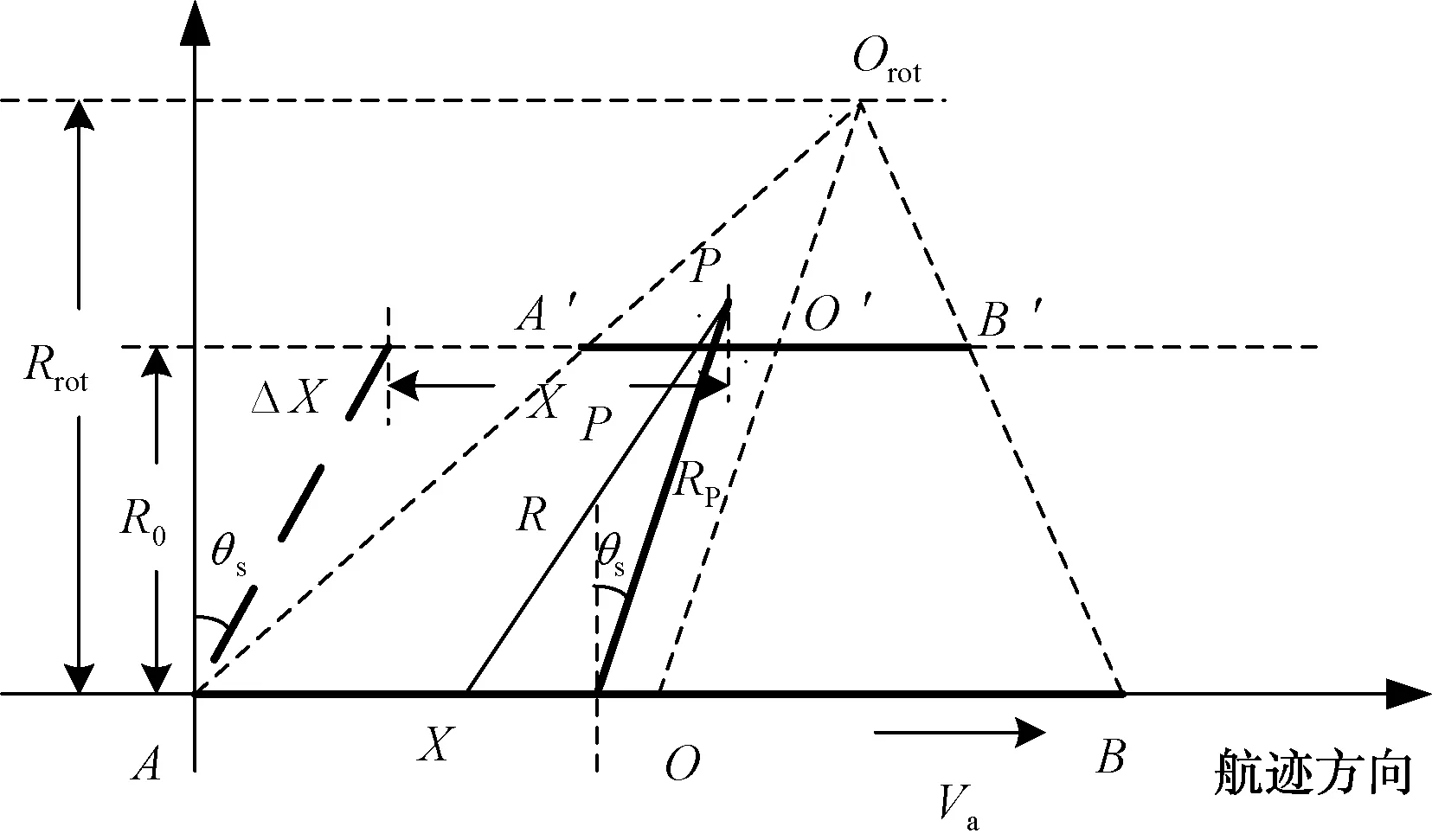
1.2 滑动聚束点目标回波方程
2 子孔径算法
2.1 子孔径算法原理
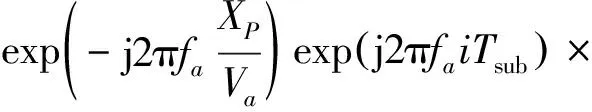
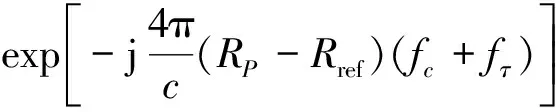

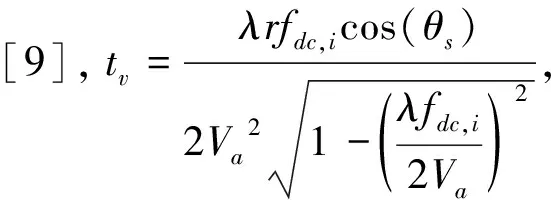
2.2 子孔径算法流程


3 实验仿真
4 结束语

