基于两类失效的产品保修策略与出保维修优化
2022-09-13尚利俊蔡志强
尚利俊, 张 驰, 蔡志强
(1.佛山科学技术学院 经济管理学院,广东 佛山 528225; 2.西北工业大学 机电学院,陕西 西安 710072)
0 引言
保修服务是在制造商和消费者(或用户)之间建立的一种合同关系,一旦产品在保修期内发生失效(或故障),制造商负责移除产品失效。保修服务既能保证产品性能,又能消除消费者对产品质量不确定的心理顾虑。从制造商角度来说,保修服务不仅能提高消费者对产品的满意度和认可度,也能树立品牌形象和带来潜在客户;从消费者的角度来说,保修服务不仅能够保障自身的权益,也能够降低保修期内的产品维修费用。
保修策略是衡量保修服务质量的一个关键指标,也是影响消费者做出购买决策的一个重要因素。基于此,制造商根据消费者对保修策略的倾向性,提供消费者偏爱的保修策略,以便提升消费者购买产品的意愿从而能进一步提升产品销量。制造商为产品提供保修服务,需承担相应的保修费用。而保修费用依赖于保修策略。根据维修方式的不同,保修策略可以分为预防维修保修策略[1~3](Preventive maintenance warranty policy)、小修保修策略[4~6](Minimal repair warranty policy)和更换保修策略[7~9](Replacement warranty policy)等。作为更换保修策略的一种特殊保修策略,更新免费更换保修策略[10,11](Renewable free replacement warranty policy)有可能使消费者免费获取相同保修的同型新产品,所以其已成为深受消费者偏爱的保修策略。
保修期是影响消费者做出购买决策的另一个重要因素。对制造商来说,为消费者提供较长保修期的保修策略,往往能满足消费者的保修需求并进一步提升产品销量。从可靠性理论的角度来讲,保修期和保修策略、产品可靠性共同影响保修费用,并且较长的保修期产生较高的保修费用。而保修费用作为成本的一部分,直接影响着产品价格、间接影响着制造商的利润。国内外学者将价格与保修联合决策作为一个重要的问题进行了研究[12~15]。然而,很少见基于更新免费更换保修策略的产品价格与保修期确定的研究。鉴于此,基于消费者偏爱的更新免费更换保修策略,从制造商的角度对产品定价与保修期确定开展研究是一个有趣的话题。
根据保修契约,为消费者提供更新免费更换保修策略的制造商负责消除产品发生的失效,但这种契约关系仅局限在保修期内。所以,如何设计出保维修策略(The post-warranty maintenance policy)以便保证出保产品的性能是消费者面对的一个问题。虽然一些研究人员和从业人员从消费者的角度对出保产品维修问题开展了广泛的研究[16~18],但存在以下问题:(1)普遍忽略了保修结束时刻的预防维修;(2)普遍以最小化费用率为目的开展了决策,忽略了以总费用为目的决策。
为了使模型具有广义性且贴近工程实践,本论文以两类失效产品为研究对象,首先在更新免费更换保修策略的条件下,从制造商角度对产品定价与保修设计开展了研究;其次,在更新免费更换保修策略的条件下,从消费者角度将保修结束时刻的预防维修融入到出保产品可靠性管理中对出保维修开展了研究。开展制造商角度的产品定价与保修设计研究,对制造商确定产品价格与保修期具有重要的决策指导意义;开展消费者角度的出保维修研究,对消费者制定保证出保产品性能的维修策略具有重要的实践指导意义。
1 产品保修效益及策略优化
1.1 基本假设
假设1产品失效是两类失效,即产品失效类型分为小修失效和致命失效;
假设2小修失效是可修失效,即可通过小修方式移除;
假设3致命失效只能通过换新方式移除;
假设4保修期内的每一次失效都产生一次对应的失效索赔;
假设5消费者购买的产品始终是由同一卖家提供的同型新产品;
假设6制造商和消费者之间的所有信息是完全的,即产品可靠性信息、保修条款和保修期内各种费用等对双方都是公开的。
1.2 产品保修过程
更新免费更换保修策略可能使消费者免费获取保修相同的同型新产品,所以其是消费者偏爱的一种保修策略。消费者的这种偏爱性表明,更新免费更换保修策略是个强有力的市场竞争策略,其定义可描述如下:
1)在保修期w内,制造商采用保修相同的同型新产品自费更换发生致命失效的产品;
2)在保修期w内,制造商采用小修的方式自费移除产品发生的小修失效。
显然,在该保修策略中,制造商采用更换或/和小修的方式移除失效。也即该保修策略包含小修和更换两种条款,所以其可被看作广义更新免费更换保修策略。
1.3 产品保修费用
进一步,令p和q(q=1-p)分别为小修失效和致命失效发生概率,令F(x)为首次失效发生时间服从的分布函数。根据文献[19],首次致命失效发生时间服从的分布函数Fq(x)可计算为
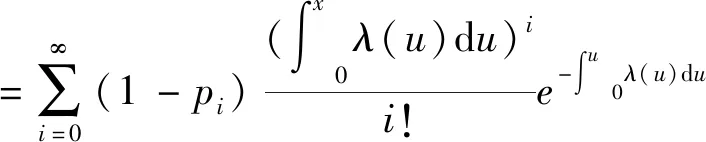
(1)
式中:λ(u)为失效率函数,其关于u(u>1)非递减。
令随机变量n为直到首个穿越保修期w的产品出现时制造商执行的更换次数,则n服从几何分布,即
(2)

直到首个穿越保修期w的产品出现时制造商执行的期望更换次数E[N(w)]为

(3)
根据保修定义,制造商负责移除保修期w内的所有小修失效。假定制造商在保修期w内每完成一次小修要花费的费用为cm(包含劳务费用、交通费用等等),根据文献[20]易知两次更换之间的期望小修次数为p/q。因此,保修期w内的每一次更换产生的期望小修费用Cmr为
(4)
制造商执行的每次更换始终是用同型新产品更换致命失效发生的产品。这表明,制造商执行每次更换要花费一个制造成本C(包含替换时花费的劳务费用、交通费用等等),同时获得一个旧产品的残值V(x)(V(x))=C-km×x,其中km(km>0)为制造商设定的折旧率)。制造成本C与残值V(x)之差就是制造商执行每次更换花费的实际更换成本CR,即
CR=C-(C-km×x)=kmx
(5)
易知保修期w内第k个致命失效发生时刻Xk(0 (6) 由(3)中的期望更换次数E[N(w)]、(4)中的期望小修费用Cmr和(6)中的期望实际更换成本E[CR],可得制造商每完成一个保修服务需花费的期望更换成本E[Cw]为 E[Cw]=E[N(w)]×(E[CR]+Cmr) (7) WC=E[Cw]+cmpΛ(w) (8) 更新免费更换保修策略可能使消费者免费获得保修期w从零开始计算的同型新产品,所以消费者更加倾向于购买拥有更新免费更换保修策略的产品。消费者的这种购买倾向性意味着,与其他保修策略相比,更新免费更换保修策略是一个更能提升产品销量的保修策略。为了建模更新免费更换保修策略这个促销功能,本论文采用一个关于保修期w且其指数ζ大于1(即ζ>1)的幂函数模型描述更新免费更换保修策略对产品销量的提升。此外,消费者倾向于购买价格较低的产品。这表明,较低的销售价格能提升产品销量。 令A为基本销量,基于上述的讨论,受更新免费更换保修策略和销售价格s同时影响的销量D(w,s)可表示为如下函数 D(w,s)=A+wζ-s (9) 式中:ζ>1。 当以销售价格s售出一个产品时,制造商需要花费的保修费用为WC(由公式(8)给出)。此时,制造商所赚取的边际利润为s-WC。进一步,制造商的利润π(w,s)可表示为 π(w,s)=(s-WC)×p(w,s) cmpΛ(w))(A+wζ-s) (10) 可转化为π(w,s)=(s-cmΛ(w))(A+w-s)。该模型为小修保修作为产品保修策略时,制造商的利润模型,相关研究可以参阅文献[21,22]等。 第二阶段:将s*代入目标函数π(w,s)中,易知目标函数π(w,s*)是一个仅关于决策变量w的指数函数;再利用数值方法计算出π(w,s*)中决策变量w的数值最优解w*,最后将其代入s*和π(w,s*)中可计算出s*的数值最优解和目标函数π(w,s)的数值最优值。 根据保修定义,制造商采用移除失效的方式保证产品在保修期w内的性能,制造商并不负责保证出保后产品的性能。因此,消费者有必要研究出保维修策略以便保证出保后产品的性能。显然,产品在出保时的年龄等于保修期长度,且产品在出保后变为可靠度小于1的旧产品(简称出保产品)。出保产品的这个可靠性特征为在保修结束时刻开展预防维修提供了理论支撑。基于此,这部分从消费者的角度,将保修结束时刻的预防维修和经典周期更换策略相融合,定义一种出保维修策略,即维修—周期更换策略。 为了分析方便,本论文定义消费者连续两次自费购买同型新产品之间的间隔为一个寿命周期。在这一部分,基于这个寿命周期,两个目标函数模型(总费用模型和费用率模型)将被推导。 (11) 根据工程实践经验,预防维修对可靠性的提升量(在本论文中,失效率函数减小量δ被用来测量可靠性提升量)越大,则相应的维修费用就越高。此外,产品年龄越大,花在可靠性提升的准备费用也就越高。这表明,维修费用既是预防维修导致的可靠性提升量(即失效率函数减小量δ)的增函数又是预防维修执行时刻w*的增函数。所以,在w*时刻的预防维修费用Cp(δ)可建模为 Cp(δ)=cm+ch(δ)a(w*)b (12) 式中:0≤δ≤λ(w*),ch>0,a>0,b>0。 (13) 假设T为更换时间。因为出保产品在区间[0,T]内可能发生致命失效,也可能发生小修失效,所以出保产品可能经历致命失效触发的事后更换、T时刻的预防更换和小修失效触发的小修。每发生一次小修失效,消费者要花费的一个小修费用cm和一个失效损失cf。因此,当在致命失效发生时刻执行事后更换时,消费者花费的小修失效费用CF(T)为 (14) 令CF为事后更换费用(包括失效损失),则当在致命失效发生时刻执行事后更换时,消费者花费的实际更换费用VF(T)为 (15) 式中:ku(ku>0)为消费者设定的折旧率。 类似于(14)中小修失效费用CF(T)的推导,当在T时刻执行预防更换时,消费者花费的小修失效费用CP(T)为 (16) 假设预防更换费用为CP(CP (17) 对(12)、(14)、(15)、(16)、(17)求和,可得在区间[0,T]内消费者花费的期望费用E[CT]为 E[CT]=CP(δ)+CF(T)+VF(T)+CP(T)+VP(T) =cm+ch(δ)a(w*)b+G(T)(CF-CP)+ (18) (19) 由上文定义的寿命周期可知,2.1节部分给出的总费用模型(即(19)中的模型)即为期望寿命周期费用。因此,当费用率被作为目标函数时,仅需要推导期望寿命周期长度,然后基于更新极限定理[24]推导对应的费用率。 2.2.1 期望寿命周期长度 (20) (21) 将(20)中的期望保修期E[W]和(21)中的期望更换时间TR(T,δ)相加,可得期望寿命周期长度LF(T,δ)为 LF(T,δ)=E[W]+TR(T,δ) (22) 2.2.2 最优费用率 (23) 假设通过对产品首次失效发生时间数据的拟合,某制造商发现其生产的产品首次失效时间服从尺度参数α=0.5(年)、形状参数β=2的威布尔分布,其对应的失效率表达式为λ(x)=αβ(αx)β-1=0.5x。为了验证利润模型、出保维修策略的有效性和说明最优解与最优值的存在性,进一步假定一些参数取常量值(见表1),其他参数当使用时再取值。 表1 参数值 基于表1中的参数,采用1.5部分中的两阶段优化方法,借助于Matlab软件获得与利润(由(10)给出)匹配的图1。由图1可知,最优保修期w*和最优利润π(w*,s*)都是唯一存在的,这表明,利润模型能开展保修设计。由1.5部分中的两阶段优化过程可知,最优销售价格s*是保修期w的单调函数。因此,当最优保修期w*是唯一存在时,最优销售价格s*也是唯一存在的。除此之外,由图1可知,最优保修期w*、最优销售价格s*和最优利润π(w*,s*)都关于致命失效发生概率q递减。 在这一部分,说明出保维修策略的有效性和性能,采用最小公倍数法[25]比较目标函数的性能,分析关键参数的敏感度。首先,验证最优维修—周期更换策略的存在性。假定w*=2(年)、q=0.06,使用表1中的参数,得到与总费用(由(19)给出)匹配的图2。由图2可知,最优维修—周期更换策略是存在的。为了使费用率模型(由(23)给出)对应的最优解和最优值更明确、直观,在q=0.25和w*=5(年)的情况下制定图3,由图3可知,最优维修—周期更换策略是存在的。其次,采用最小公倍数法比较两种目标函数的性能。假定w*=2(年)、LC1和LC2分别为在最小公倍数情况下两种目标函数对应的寿命周期费用。数值分析结果如表2所示。 表2 目标函数的性能比较 由表2可知,①当费用率为目标函数时,最优期望寿命周期费用LC(T*,δ*)、最优期望寿命周期长度LF(T*,δ*)都是关于致命失效发生概率的增函数;②当总费用为目标函数时,最优期望寿命周期费用LC(T*,δ*)是关于致命失效发生概率q的增函数,而最优期望寿命周期长度LF(T*,δ*)是关于致命失效发生概率q的增函数;③在致命失效发生概率q相同的情况下,寿命周期费用LC1始终小于寿命周期费用LC2(即LC1 第三,分析当总费用作为目标函数时,维修—周期更换策略的性能。假定w*=2(年)、LC1和LC2分别为不进行非完美维修(即CP(δ)=0、δ=0,此时维修—周期更换策略转化为经典周期更换策略)和进行非完美维修对应的寿命周期费用(即在最小公倍数的情况下),得到数值分析结果如表3所示。 表3 总费用对应的维修—周期更换策略性能 由表3可知,当不进行非完美维修(进行非完美维修)时,最优期望寿命周期费用LC(T*,0)(LC(T*,δ*))是关于致命失效发生概率q的增函数,而最优期望寿命周期长度LF(T*,0)(LF(T*,δ*))是关于致命失效发生概率q的减函数;在致命失效发生概率q相同的情况下,不进行非完美维修对应的寿命周期长度LF(T*,0)小于进行非完美维修对应的期望寿命周期长度LF(T*,δ*)(即LF(T*,0) 第四,分析当费用率作为目标函数时,维修—周期更换策略的性能。假定w*=2(年),在进行非完美维修和不进行非完美维修(即CP(δ)=0、δ=0,此时维修—周期更换策略转化为经典周期更换策略)的情况下,得到表4。由表4可知,当进行非完美维修(不进行非完美维修)时,最优费用率C(T*,δ*)(C(T*,0))是关于致命失效发生概率q的增函数,而最优期望寿命周期长度LF(T*,δ*)(LF(T*,0))是关于致命失效发生概率q的减函数;在致命失效发生概率q相同的情况下,进行非完美维修对应的费用率C(T*,δ*)小于不进行非完美维修对应的费用率C(T*,0)(即C(T*,δ*) 表4 费用率对应的维修—周期更换策略性能 本论文,首先从制造商角度构建了两类失效情况下产品的保修费用,并在其为制造成本的情况下对产品开展了产品定价与保修设计研究;其次,从消费者角度将预防维修与经典周期更换策略相融合,提出了维修—周期更换策略,并在其为出保维修策略的情况下,构建了两个目标函数:期望寿命周期总费用和费用率;第三,使用数值实验,先从制造商角度对产品价格和保修期对应的最优解存在性进行了说明,然后采用最小公倍数法从消费者角度对最优维修—更换策略的存在性和各个目标函数的性能进行了说明与比较。比较发现:费用率模型性能更优、提出的维修—周期更换策略性能更优。
1.4 产品销售利润
1.5 产品保修策略优化

2 产品出保效益及维修优化
2.1 出保维修总费用




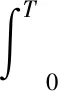
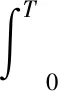


2.2 维修费用率优化

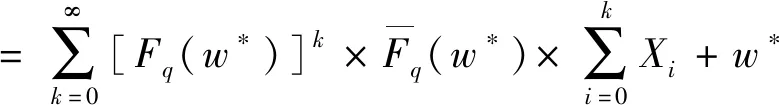
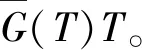




3 数值实验验证

3.1 产品保修策略优化
3.2 产品出保维修优化



4 结论
