面向远海岛屿的救助基地选址优化模型及其算法

王翊萱, 王 诺, 高忠印, 吴 迪, 林婉妮

(大连海事大学 交通运输工程学院,辽宁 大连 116026)

0 引言

所谓远海岛屿，是指远离大陆，难以直接获得陆地支援的岛屿。当远海发生海难事故时，由于海上人命救助的时效性极强，救援的黄金时机稍纵即逝，从大陆救助基地调遣救援力量赶赴现场施救效率过低，因而需要在远海岛屿设立救助基地以缩短驰援时间[1]。但因远海救助基地投资巨大，所以涉及诸多问题一直难以解决[2]。随着我国海运的迅速发展，海上航行安全的重要性日益凸显，在远海海域选择岛礁建设救助基地已成为当前亟需解决的重要问题，这对于提高远海海上的响应能力具有重要意义。

有关海上救助值班点的选择问题，目前已有部分研究成果，如基于加权费马点原理，建立针对南海的救助动态值点选址模型[3]；利用P-中值建立了应急救助站点选址模型[4]。关于海上救助力量的配置问题，有的学者针对海上溢油应急处置问题提出了一套相应的应急船舶调度方案[5]，通过分析船舶的分布密度、类型、性能和地理因素等分配搜救资源[6]。关于救助基地的选址问题也有一些可供借鉴的成果，如以受灾点的需求为变量，以救援时间为约束，建立以总运输成本最小为目标的应急救援中心选址模型[7]。近年来，关于GIS在海事救助领域的应用研究也有所增加，其内容主要包括模拟浮标漂移轨迹、确定搜索区域以及跟踪漂移浮标运动，对目标实时监控和信息化管理，提高应对海上突发事故的能力[8,9]等。

分析以上文献可以看到，尽管相关研究已有一些成果，但在面向远海岛屿进行救助地基选址的优化方法研究方面仍存在明显空白。有鉴于此，本文以远海岛屿优化救助基地选址为研究目标，以海域救助值班点选择、救助船舶配置及救助基地建设成本估算为基本内容，以建设运营总成本最低和对过往商船覆盖率最大为优化目标，结合现代技术手段，提出了新的优化模型和求解方法，其主要工作和贡献是：①基于GIS空间分析功能，采用模糊C-均值聚类算法对研究区海域往来船舶密度进行聚类，求出救助动态值班点的较佳分布；②从整个边远海域救助系统角度出发，建立考虑建设总成本最小和过往商船覆盖率最大的双目标优化模型；③引入自适应拉伸的拥挤距离公式，设计了自适应精英保留策略的NSGA-II算法对模型进行求解。最后，以我国南沙岛礁群救助基地选址及配置救助船舶为例，验证了本文优化模型和算法的可行性和有效性。

1 模型分析

1.1 问题描述

本文需优化的目标有两个，一是如何选择海上救助值班点，使其对过往船舶的覆盖面尽可能地大，以提高海上救援效率；二是如何选择可提供救助船舶停泊的基地数量和位置，使其建设和运营成本尽可能地少，以节省救援设施的费用。为此，本文面临的问题是：①若动态值班点的数量过少，则对远海海域的覆盖面积减小，若偏远海域发生海难，则救助船舶无法在最短时间内赶到，救助成功率降低；而若动态值班点数量过多，则需配备更多的救助船舶，其成本势必会增加，因此如何确定动态值班点的数量及位置是需要解决的第1个问题；②因我国大型救助船舶的数量较少，若在每个值班点均配置大型救助船舶，则需要更高的购置成本；而若配置中型救助船舶，又难以达到理想的救助海域覆盖率，因此如何为每个值班点配置适当船型是需要解决的第2个问题；③若选择只建设1个救助船舶基地，虽会明显降低泊位的建设成本，但势必造成动态值班点与基地的距离过远，使得救助船舶回基地补给的航行时间增加、运行效率降低；而若建设多个救助基地，则初期投资成本将激增，因此如何确定救助基地的数量与位置是需要解决的第3个问题。上述3个问题涉及的变量众多，且相互交叉，因而需统筹优化。

1.2 符号设定

I表示商船集合，其编号i∈I；J表示动态值班点集合，其编号j∈J；K表示岛礁集合，其编号k∈K；P表示泊位类型集合，其编号p∈P；S表示救助船型集合，其编号s∈S；xi表示商船i的位置；yj表示动态值班点j的位置；U表示隶属度集合；uij表示商船i隶属于动态值班点j的隶属度，且有uij∈[0,1]，uij∈U；Ij表示动态值班点j覆盖的商船集合(Ij⊆I)；Pk表示岛礁k可以建设的泊位类型集合(Pk⊆P)；Sp表示p类型泊位可以挂靠的救助船型集合(Sp⊆S)；dij表示商船i与动态值班点j的距离；ljk表示动态值班点j与岛礁k的距离；αp表示各岛礁建设p类型泊位所需的单位建设成本；τ表示临界响应时间阈值，即海上人命存活最大时间；vs表示s型救助船舶的速度；βs表示s型救助船舶的单位购置成本；δs表示s型救助船舶单位距离航行成本；δs表示s型救助船舶年运营成本；C表示各岛礁建设救助基地的固定成本；Qs表示s型救助船舶的最大数量；Ukp表示岛礁k可建设p类型泊位的最大数量；γ表示0-1变量，用于调节约束条件；Wk表示0-1变量，当岛礁k被选为救助基地时Wk=1，否则Wk=0；Zkp表示整数变量，岛礁k建设p类型泊位的数量；Xjs表示0-1变量，当为动态值班点j配置s型救助船舶时Xjs=1，否则Xjs=0；Yjk表示0-1变量，当动态值班点j的救助船依托岛礁k的救助基地时Yjk=1，否则Yjk=0。

1.3 模型建立

1.3.1 海上救助动态值班点选择模型

根据海上救助船舶资源现状及航行商船密度分布，以各艘商船到各个动态值班点的加权距离之和最小为目标，建立海上救助船舶动态值班点选择模型，即：

(1)

(2)

其中，式(1)为目标函数，表示各个商船到各个动态值班点的加权距离之和最小；式(2)表示各个商船到所有动态值班区域的隶属度之和为1。

1.3.2 海上救助船舶配置及救助基地选址模型

基于式(1)得到的海上救助动态值班点的位置坐标，以总投资成本最少和过往商船覆盖率最大为目标，建立海上救助船舶配置和救助基地选择模型，即：

(3)

(4)

s.t.Ij={i|i∈I,Xjsvs/dij≤τ}

(5)

WkZkp≥Zkp,∀k∈K;∀p∈P

(6)

Zkp≤Ukp,∀k∈K;∀p∈P

(7)

(8)

(9)

(10)

(11)

(12)

Zkp≤M(1-γ),∀k∈K;∀p∈P

(13)

(14)

(15)

其中，式(3)表示总成本最小，其中依次为建设救助基地固定成本、泊位建设成本、救助船舶的购置和运营成本、救助船舶航行成本；式(4)表示过往商船覆盖率最大。式(5)～式(15)为约束条件。式(5)表示在动态值班点j处配置s型救助船舶所能覆盖的过往商船必须在其临界响应时间范围内；式(6)表示只有当岛礁被选定为救助基地时才能建设泊位；式(7)表示在岛礁k建设p类型泊位的数量必须要小于等于其所能建设的最大数量；式(8)表示岛礁k可建设的泊位类型必须在其自身条件限制内；式(9)表示救助船舶数量限制；式(10)表示动态值班点j上最多只允许配置1艘救助船舶；式(11)表示如果动态值班点j没有配置救助船舶，则不需要依托救助基地；式(12)表示动态值班点j配置了救助船舶后，必须且只能依托一个救助基地；式(13)和式(14)表示动态值班点j选择依托的救助基地必须有能供其s型救助船舶挂靠的泊位类型；式(15)表示岛礁k建设的泊位数量必须能够供选择该岛礁作为依托的救助船舶同时挂靠。

2 计算方法

2.1 海上动态值班点选择计算模块

要划分海上动态值班点，其优化思路是以各过往商船到动态值班点的加权距离最短为目标，将商船划分为不同类别，以实现选取适当的各类别中心点将其作为动态值班点。本文采用模糊C-均值聚类算法进行分析，该算法通过优化目标函数得到每个样本点对所有类中心的隶属度，从而实现对样本数据进行分类。为此，令式(1)中的Gf分别对yj和uij求偏导，取偏导数为0作为其极小值的必要条件，最终得到隶属度矩阵U*和值班点集合J*，其表达式如下:

(16)

(17)

其中，式(16)计算动态值班点的坐标，式(17)计算各个商船的隶属度，在[0,1]之间的随机数初始化隶属度矩阵，式中其他符号意义同上。

2.2 海上救助船舶配置及救助基地选址计算模块

2.2.1 染色体设置

本文编码染色体包括4部分信息：①各动态值班点配置的救助船舶类型；②可被选为救助基地的岛礁编号；③各动态值班点救助船舶所依托的救助基地编号；④被选为救助基地后应建设何种类型的泊位编号，以及每种类型泊位应建设的数量。为表达上述信息，本文构造2条染色体，如图1所示。

2.2.2 算法改进

对于本文问题，传统的NSGA-II算法存在解集收敛性和分布性较差的缺陷，使得求解时难以有效获得优质的Pareto非劣解。因此，为使得算法能够得到分布性较好且更为优质的解，本文从分布性和精英保留策略两方面对算法进行改进。

对于分布性，NSGA-II的拥挤距离计算公式如下:

(18)

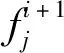
NSGA-II算法在运行初期，因个体差异较大，所以利用式(18)可以获得较好的效果。但在运行后期，会出现优秀个体优势不足，不利于解集形成较好的分布性。为弥补这一缺陷，本文提出一种自适应拉伸拥挤距离，其计算式为:

(19)

其中，N为种群中个体数量，T0为初始温度，λ为降温影响因子，k为迭代次数。

对于精英保留策略，由于传统的NSGA-II算法在选取精英个体规模时存在两难选择：若选取规模较小，则容易失去优良的个体；若选取规模过大，则影响下一代的多样性。对此，本文提出一种自适应精英保留的策略，其计算式为:

Ek=N×αk

(20)

其中，αk表示第k代进化过程中精英保留规模的影响因子，Ek表示第k代进化中精英个体的数量，N为种群规模。αk的自适应迭代公式如下:

αk=αmin+k(αmax-αmin)/Rmax

(21)

其中，Rmax表示最大迭代次数，αmax取0.8，αmin取0.2。

2.3 最优解选择

利用以上算法可以得到一组Pareto非劣解集，但若要得出最优解，还需根据决策者的偏好进行选取。为此，本文参照文献[10]的成果，根据Pareto前沿的几何分布特点，选择相对于两个优化目标平均变化率最灵敏的交点所对应的解，即为性价比最优的解。

2.4 计算步骤

本文算法流程如图2所示。

3 实例分析

现以我国将在南沙群岛海域就建设救助基地选址和救助船舶配置的优化过程为例进行分析。

3.1 基础数据

关于南海南沙群岛附近海域(2°00′N～14°00′N，105°00′E～119°50′E)中过往商船的分布数据来源于美国国家海洋和大气管理局[11]，结合南沙群岛的自然条件，对各岛礁可建的泊位规模进行评估(表1)。

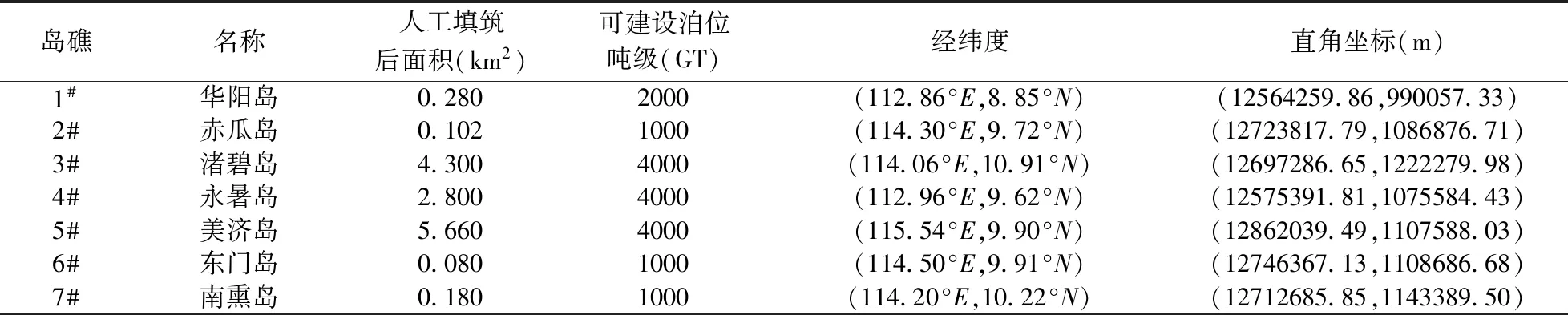
表1 南沙主要岛礁位置及可建设泊位条件

对于救助船舶的配置，按照我国《海事船舶配备管理规定》中关于救助船舶的配置标准，因南沙群岛海况恶劣，只有60米级及以上较大类型的救助船舶可以承担边远海域的应急任务[12]。考虑到目前我国能够承担远海巡逻任务的60米级以上中大型救助船舶约10艘左右[13]，因此本文以10艘救助船舶为基数进行配置计算，其代表船型的基本参数见表2。

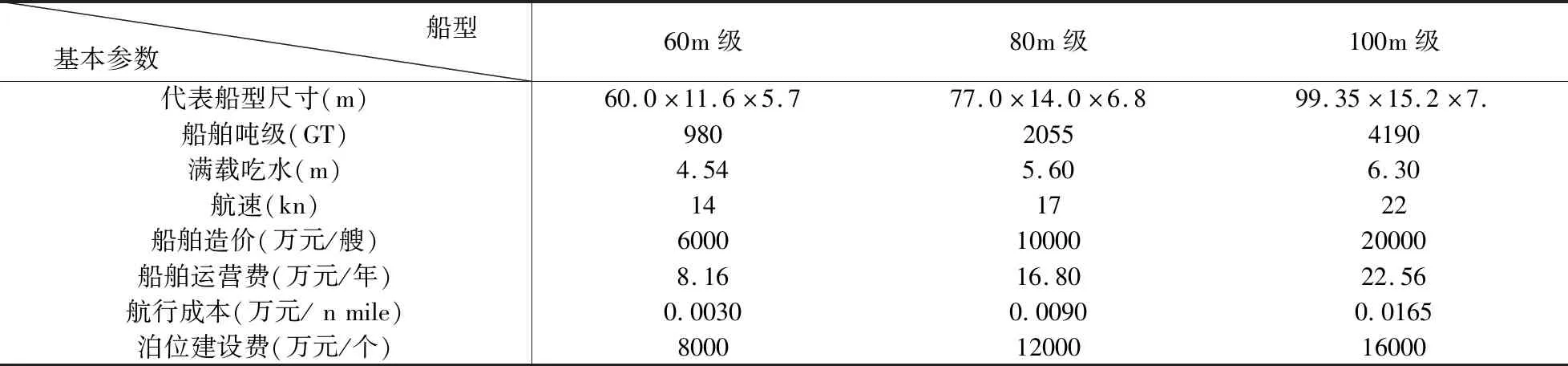
表2 救助船舶船型、性能及营运成本有关参数

3.2 计算结果

使用Python语言编程，选用处理器为8G inter(R) i7-8750H，运行环境为ArcMap 10.6。根据模糊C-均值聚类算法对船舶数据进行聚类，得到10个类，每个类的动态值班点坐标见表3。设救助船舶临界响应时间阈值δ=5h，NSGA-II算法的种群数量为30，交叉概率0.8，变异概率0.05，迭代次数500次。

表3 动态值班点坐标

经计算得到Pareto解的偏向度见表4，其中，Pareto解偏向度最小的方案为2#方案，其最优方案为：①关于救助基地选址：可在永暑岛建设泊位4个，其中，4000吨级泊位1个、2000吨级泊位1个、1000吨级泊位2个；在华阳岛建设泊位2个，其中，2000吨级泊位1个、1000吨级泊位1个；在渚碧岛建设泊位4个，其中，2000吨级泊位3个、1000吨级泊位1个；在赤瓜岛、美济岛、东门岛、南薰岛不建设基地(表5)；②关于救助船舶配置：在动态值班点1#配置100m级救助船舶1艘；在动态值班点2#、3#、4#、6#、8#各配置80m级救助船舶1艘；在动态值班点5#、7#、9#、10#各配置60m级救助船舶1艘；③关于动态值班点的依托基地：前往动态值班点1#、4#、7#、9#的救助船舶依托永暑岛救助基地；前往动态值班点2#、3#、5#、6#的救助船舶依托渚碧岛救助基地；前往动态值班点8#、10#的救助船舶依托华阳岛救助基地(图3)。

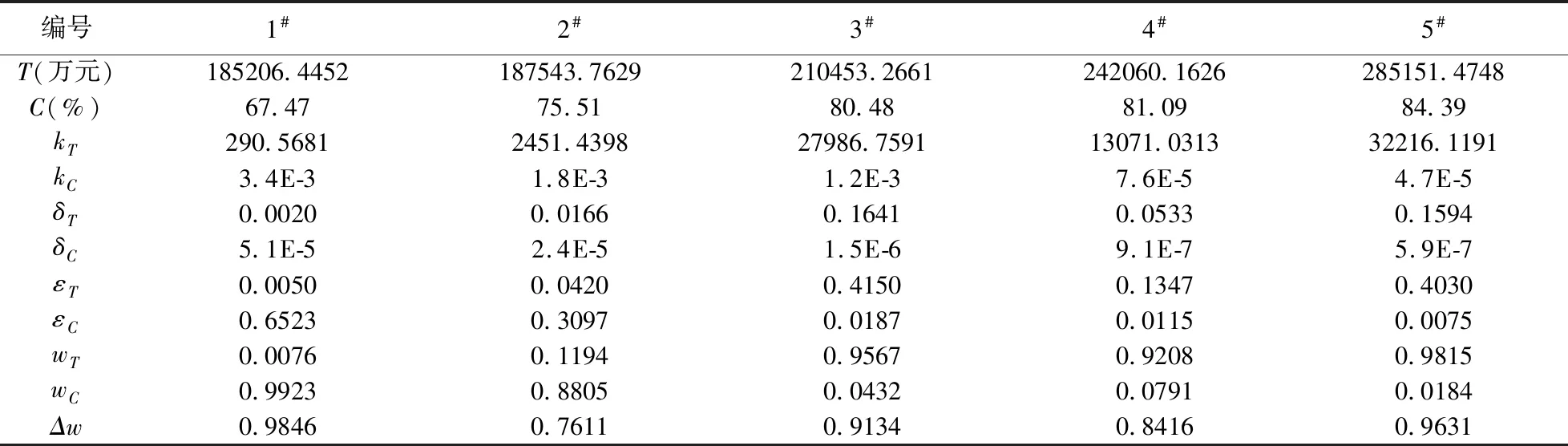
表4 Pareto非劣解集对应的参数表

表5 各岛屿救助船舶泊位建设方案

注：该图基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1609号的标准地图制作，底图无修改。

3.3 算法比较

为验证算法改进后在扩大规模情况下的计算效果，以上述算例和算法参数为基础，采用2组不同规模算例进行对比，设算例1为10个动态值班点、7个候选救助基地；设算例2为15个动态值班点、7个候选救助基地。计算结果显示：从计算10次得到的SP(间距指标)值上来看，本文算法求得的SP指标在平均值上改进幅度为23.09%～27.64%、在最小值上改进幅度为18.10%～31.53%、在标准差上改进幅度15.99%～33.38%，表明本文算法求得的解集均匀性较好(表6)。综上，改进NSGA-II算法获得解的优化结果更好，且具有良好的分布性(图4)。

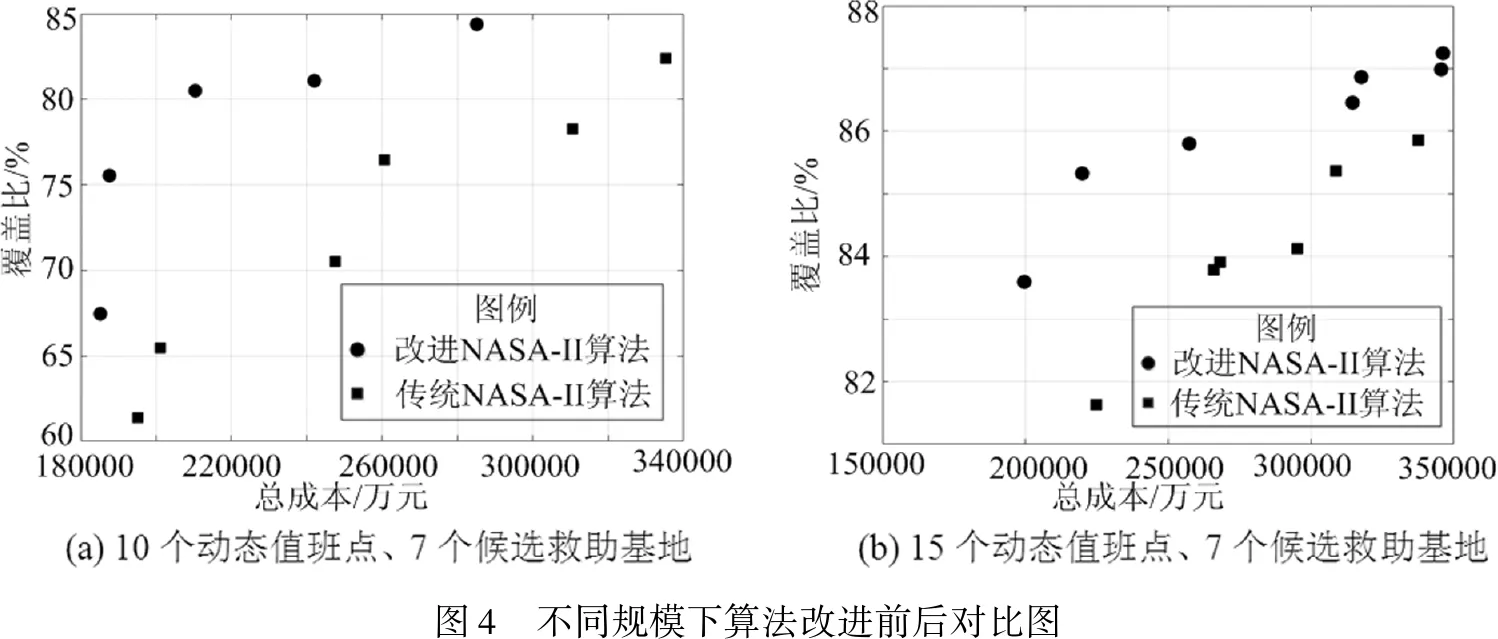
表6 算法改进前后不同规模计算结果对比

4 结论

本文面向我国当前亟需解决的科学问题，以远海岛屿优化救助基地选址为背景，以海域救助值班点选择、救助船舶配置及救助基地建设成本优化为基本内容，以建设运营总成本最低和对过往商船覆盖率最大为优化目标，建立考虑建设总成本最小和过往商船覆盖率最大的双目标优化模型。基于GIS的空间分析功能，采用模糊C-均值聚类算法对研究区海域往来船舶密度进行聚类，求出救助动态值班点的较佳分布；引入自适应拉伸的拥挤距离公式设计自适应精英保留策略的NSGA-II算法对模型进行求解。通过我国在南沙岛礁群案例，验证了本文模型及算法的可行性，从而为我国海上岛屿救助基地选址和在救助资源有限的情况下如何科学配置提供了分析方法。

需要指出，本文仅以救助船舶为救援主体开展研究，而实际中救助力量还配备有直升机等救援工具，此种情况下救助动态值班点选择、救助力量配置、救助基地选址等的优化模型将会更加复杂，此类问题是下一步需要研究的内容。