异形型腔电解加工多物理场耦合仿真研究

徐天赐，贾建利，钟 毅，李圣辰

(1.西安工业大学 机电工程学院，西安 710021；2.重庆市地勘局 205地质队，重庆 402160)

随着科技、新兴工业以及精密毛坯的发展，精密仪器、精密模具制造在现代制造业中的重要性和占比越来越大，电解加工因具有不受工件材料限制、表面质量好、无切削应力等优点，在这个领域占据了重要地位[1]。由于电解加工涉及多个物理场耦合影响，使得加工过程复杂，加工后形貌难预测，对此国内外诸多学者借助计算机仿真技术进行了大量的研究。

文献[2]对四种不同结构的阴极进行仿真，探究了流场、温度场及电场的分布规律，预测了工件的成型形貌。文献[3]对电解加工过程中电场的作用规律进行探究，得到了材料去除率及电压之间的关系。文献[4]以钛合金方孔为研究对象，建立了钛合金方孔电解加工多物理场耦合模型，探究了各物理量随加工时间的变化规律。文献[5]通过仿真模拟探究了电解液的温度、导电系数、离子传输、反应产物、及电解液流速对电解加工过程产生的影响，精准预测了加工后工件形状。文献[6]针对具有内部特征的微孔，提出了一个多物理场模型来探究加工参数对温度和气泡的影响，通过优化加工参数实现了加工精度的提升。文献[7]针对加工间隙中温度难以测量的问题，采用数值计算的方法对温度场进行仿真，结果表明采用壁函数求解温度场的结果更加精确。以上研究均是在二维模型以及简单的三维模型下进行，对于较为复杂的三维模型目前研究还不够充分。

文中通过COMSOL软件，建立了电场、流场、温度场及结构场的多物理场耦合模型，探究在不同入口流速下，间隙内电解液流速、温度、电流密度的分布以及工件阳极表面的成型精度和形貌的变化，为复杂结构型腔的电解加工提供了工艺技术参考。

1 模型建立

1.1 几何模型建立

“T”形型腔电解加工几何模型如图1所示，供液形式采用正流式，包括：带通孔的“T”形工具阴极，电解液流动区域，以及长方体形工件。工件阳极与工具阴极分别与电源正负极相连，电解液在加工间隙内高速流速，在外加电场的作用下，工件阳极表面不断溶解，阴极析出氢气，直至完成最终的加工。

图1 电解加工几何模型示意图

1.2 流场模型

流体运动有层流和湍流两种形态，依据雷诺数进行判断，当雷诺数Re<2 300为层流，Re>2 300为湍流。根据加工条件进行计算，流速v=3 m·s-1，水力直径d=5 mm，20 ℃时电解液动力黏度近似为水，取1.01×10-6，经计算得

(1)

加工间隙内流场为湍流。根据能量守恒定律及质量守恒定律可知，设定流体微元在流场中的位置坐标为(x,y,z)，流体流动方程[8]为

(2)

式中：ρ为流体密度；u，v,ω为流速在x，y,z方向上的分量；p为流体微元压力值；μ为动力黏度；t为时间；g为重力加速度；∇为梯度算子；∇2为拉普拉斯算子；∇·V为体积膨胀率；V为体积。

在流场数值仿真中，重整化群k-ε模型应用范围最广，对于不可压缩流体，其方程[9]为

(3)

式中：xi,xj为流体微元在流场中的位置坐标；μi，μj为湍动黏度；Gk为平均速度梯度引起的湍动k的产生项；ε为湍动耗散率；Cc1，Cc2，Cμ，σk，σε，K为常数，且Cc1=1.44，Cc2=1.92，Cμ=0.09，σk=1.0，σε=1.3，K=0.41。

1.3 温度场模型

加工间隙产生的焦耳热以及电极反应产生的热，是电解加工过程中热量的主要来源，由于后者产生的热量较小，可忽略不计，由欧姆定律可知加工间隙产生的热量[10]为

(4)

式中：i为电流密度；φ为电势；σ为温度系数；U为加工电压；Δ为加工间隙。

在加工过程中，加工间隙产生的热量受到流场和电场的影响，满足对流-扩散方程[11]：

(5)

式中：Cp为电解液比热容；T为温度；k1为电解液导热率；Q为加工中产生的热量。

1.4 电场模型

由电荷守恒可知，电势U满足以下关系式：

∇(C∇U)=0，

(6)

其中C为电解液电导率。

电解液电导率通过与温度相关的线性模型[12]来定义：

C=C0[1+γ(T-T0)],

(7)

式中：C0为初始电导率；γ为温度相关系数；T0为初始温度。

1.5 耦合模型

电解加工中涉及多个物理场，包括流场、电场、温度场及结构场，其耦合关系如图2所示。

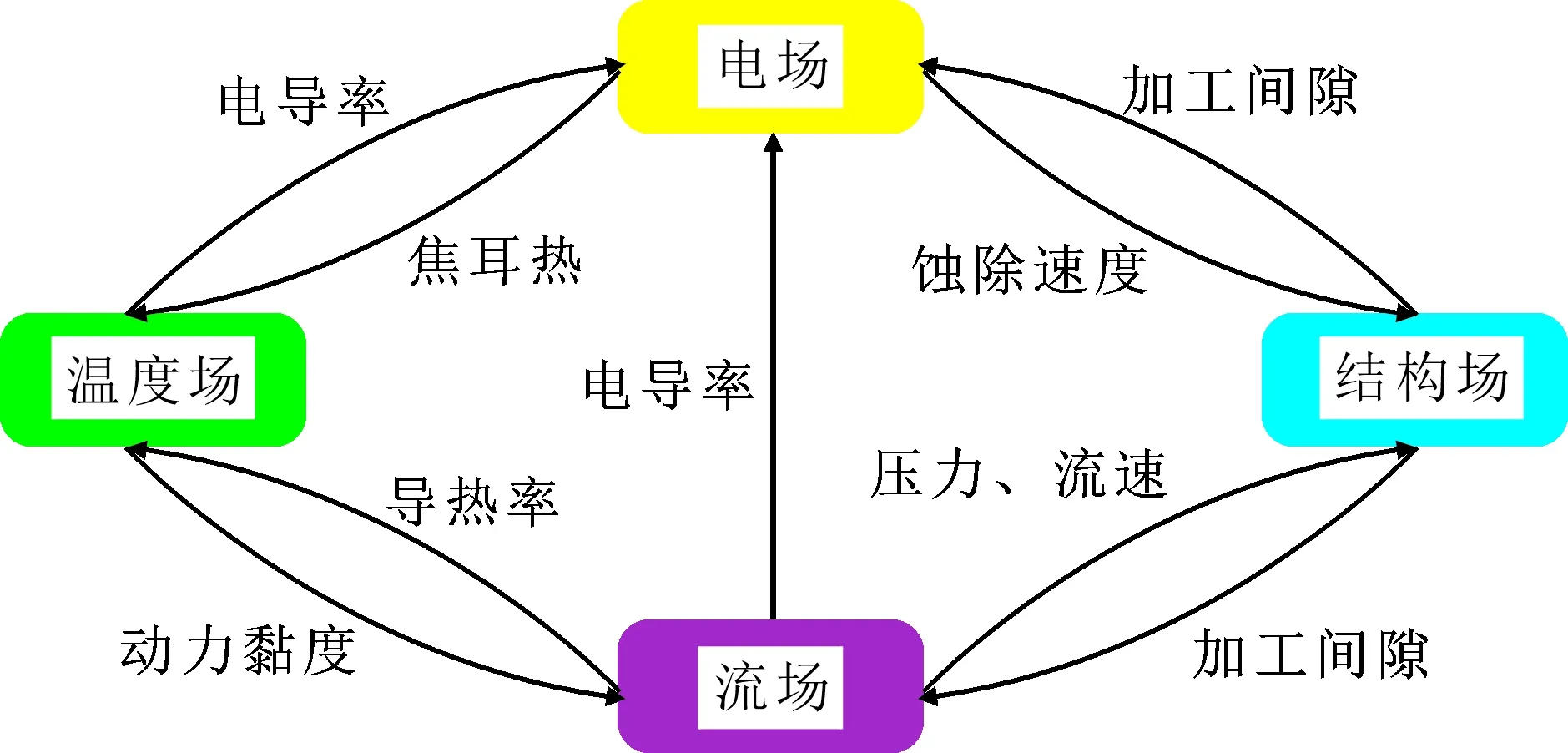
图2 多物理场耦合关系示意图

根据能量方程,加工间隙的温升为

(8)

其中L为流程。电场、流场及温度场耦合方程[11]为

(9)

阳极表面溶解速度为

Va=C0[1+γ(T-T0)]∇φ。

(10)

1.6 仿真参数条件

为了更加符合实际加工环境，在仿真中对阳极反应界面施加终止函数step(cd.itot/i_threshold-1)，其中step为阶跃函数，cd.itot为阳极表面电流密度，i_threshold为蚀除阈值电流密度，当加工间隙处于切断间隙时，阳极表面停止蚀除，仿真参数见表1。在仿真后的阳极表面上取x和y方向两条截线AB和CD，并在截线上各取60个测量点，截线如图3所示。

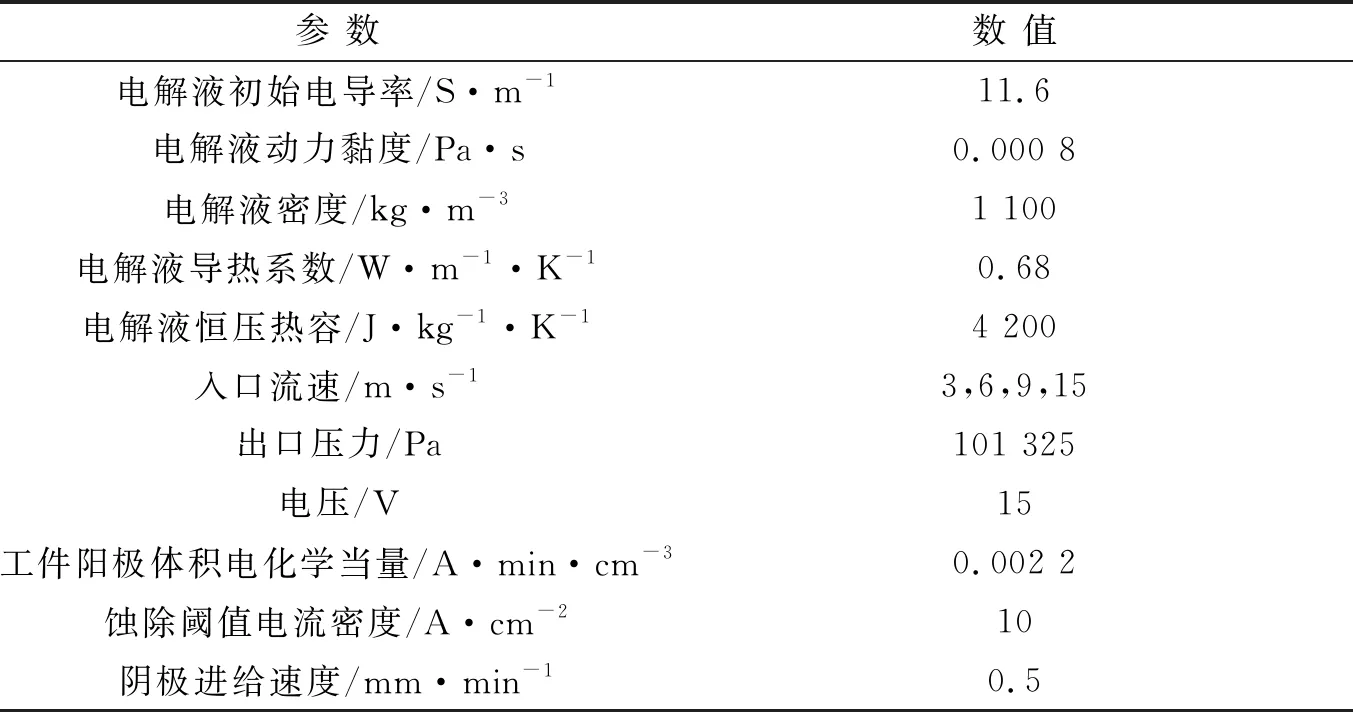
表1 仿真参数

图3 截线AB和CD示意图

2 结果分析与讨论

2.1 不同入口流速对间隙内电解液流速分布影响

流场在多物理场耦合中非常关键，在加工中不同的入口流速，会对间隙内电解液流速的分布及流场的均匀性产生显著影响。文中通过对3 m·s-1，6 m·s-1，9 m·s-1及15 m·s-1时入口流速状态下间隙流场进行仿真分析，结果如图4～5所示。

从图4～5中可以看出，电解液流速分布沿着工具阴极底面向外扩散流动，工具阴极底面对电解液流动起到了导流作用。通液孔底部为高流速电解液与工件表面最初接触位置，电解液高流速能量释放，电解液流动产生局部瞬时停滞，导致流速极小。当入口流速为3 m·s-1时，电解液最大流速为12.2 m·s-1，且在通液孔四周呈现均匀分布，但工具阴极末端边缘区域的电解液流速降低到5 m·s-1以下，在实际电解加工过程中，当电解液流速降低至5 m·s-1以下，极大可能产生钝化现象，造成阳极溶解产物及热量无法及时排出，阻碍下一步加工。提升入口流速至6 m·s-1，9 m·s-1及15 m·s-1，间隙内最大电解液流速分别提升至25.3 m·s-1，38.0 m·s-1，63.0 m·s-1，工具阴极末端边缘区域的流速均达到5 m·s-1以上，能够有效避免钝化现象。

图4 间隙电解液流动分布云图

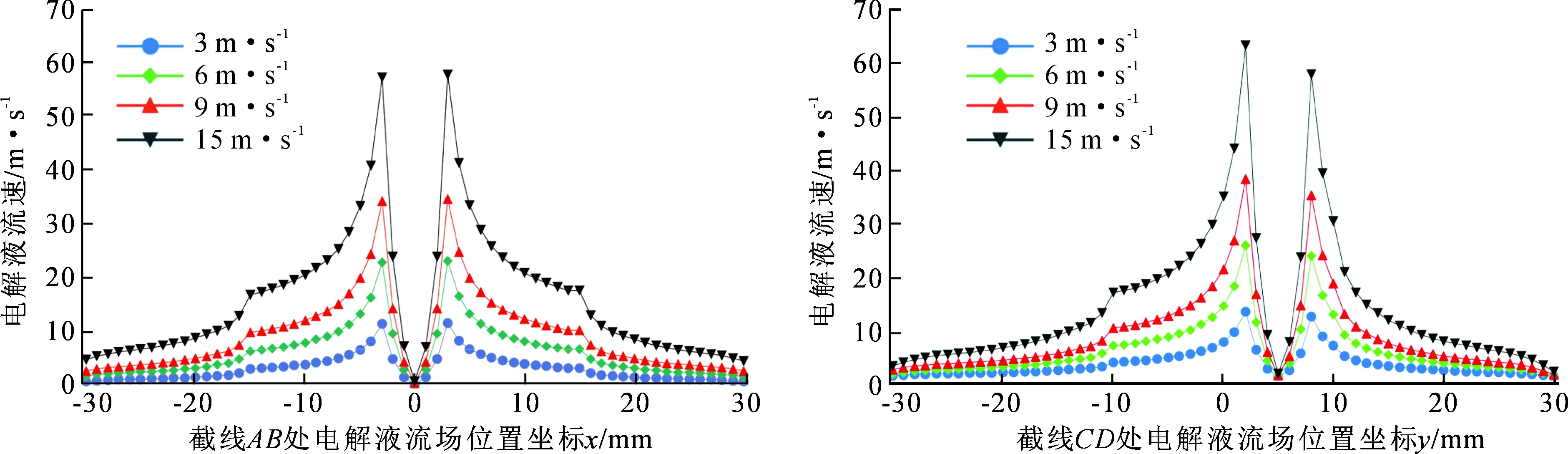
图5 电解液流速分布

2.2 不同入口流速对间隙内电解液温度分布影响

在电解加工过程中，间隙内流动的电解液可视为电阻，当工具阴极和工件阳极通电之后，电流流经电解液时所产生的焦耳热、工件阳极氧化反应产生的腐蚀放热为加工间隙内热量的主要来源。电解液温度的高低是决定加工间隙内电解液电导率大小的关键因素之一，图6所示仿真结果表明了，工具阴极底部末端边缘区域电解液温度较高，这是由于电解液在工具阴极底部末端边缘区域流速相对较低，热传导效率低，造成在该位置处电解液温度较高。在实际电解加工过程中，间隙内电解液温度不宜过高，通常为20 ℃～25 ℃。根据仿真结果，当入口流速为3 m·s-1时，间隙内电解液最高温度达到47.1 ℃。当入口流速为6 m·s-1，9 m·s-1及15 m·s-1时，间隙内电解液最高温度降低。当间隙内电解液流速大于5 m·s-1时，电解加工过程钝化现象减少,甚至可以避免，电解液温度大幅下降，并且入口流速为15 m·s-1时，电解液温度处于最佳温度范围。因此，当入口流速为6 m·s-1及以上时，能够避免钝化现象对电解液温升产生的不利影响，显著提高了加工效率,实现了成型精度和形貌变化可控。

图6 电解液温度分布

2.3 不同入口流速对间隙内工件阳极表面电流密度分布影响

在“T”形型腔的实际加工成型过程中，在多个物理场相互耦合、相互作用下，流场、温度场对工件阳极成型形貌的影响规律最终取决于工件阳极表面的电流密度分布情况。通过多物理场耦合仿真分析得到工件阳极表面电流密度分布，如图7所示。从图7中可看出，工件阳极表面电流密度分布不均匀，其分布显著地受到电解液温度分布的影响，温度高的位置电流密度大，温度低的位置电流密度小。当入口流速为3 m·s-1时，位于工具阴极底部末端边缘区域电解液流速小于5 m·s-1，间隙内电解液温差较大，产生显著钝化现象，进而导致工件阳极表面电流密度分布极不均匀，并且电流密度较大区域集中在工具阴极底部末端边缘区域位置，最大电流密度达到95 A·cm-2。当入口流速为6 m·s-1，9 m·s-1和15 m·s-1时，间隙内电解液流速均大于5 m·s-1，减少甚至避免钝化现象的影响，使得间隙内电解产物及热量能够及时排出，工件阳极表面电流密度分布得到极大改善，最大电流密度分别降低至76 A·cm-2，68 A·cm-2，65 A·cm-2。当电解液流速为15 m·s-1时，工件阳极表面电流密度分布最均匀。

图7 阳极表面电流密度分布

2.4 不同入口流速对间隙内工件阳极表面成型形貌影响

在多物理场、流场及温度场共同作用下，通过施加自由结构形变场可得到加工150 s后工件阳极型腔三维形貌和AB、CD截线形貌，如图8～9所示。从图8可看出，当入口流速为3 m·s-1时，由于间隙内电解液在工具阴极底部末端边缘区域流速小于5 m·s-1，产生钝化现象，造成在该位置区域电解液温度较高，且工件阳极表面电流密度较其他位置大，导致其蚀除量明显大于其他位置，最大蚀除深度达到4.63 mm。当电解液入口流速增大至6 m·s-1、9 m·s-1及15 m·s-1时，间隙内电解液流速均大于5 m·s-1，减少甚至避免了钝化现象的产生，最大蚀除深度分别减小至3.81 mm、3.62 mm及3.42 mm，“T”形型腔最大蚀除深度随着间隙内流速提升而减小，当间隙内电解液流速大于5 m·s-1时，工件阳极各位置电流密度分布趋于均匀，工件阳极各个位置蚀除深度差异逐渐减小。从图9可看出，当入口流速为3 m·s-1时，“T”形型腔形貌呈现中间高边缘低，使得型腔底面具有较大斜率；当入口电解液流速提升至6 m·s-1、9 m·s-1及15 m·s-1时，此时“T”形型腔蚀除深度趋于均匀，各个位置尺寸误差得到有效改善，型腔底面斜率大幅减小。

图8 “T”形型腔三维形貌

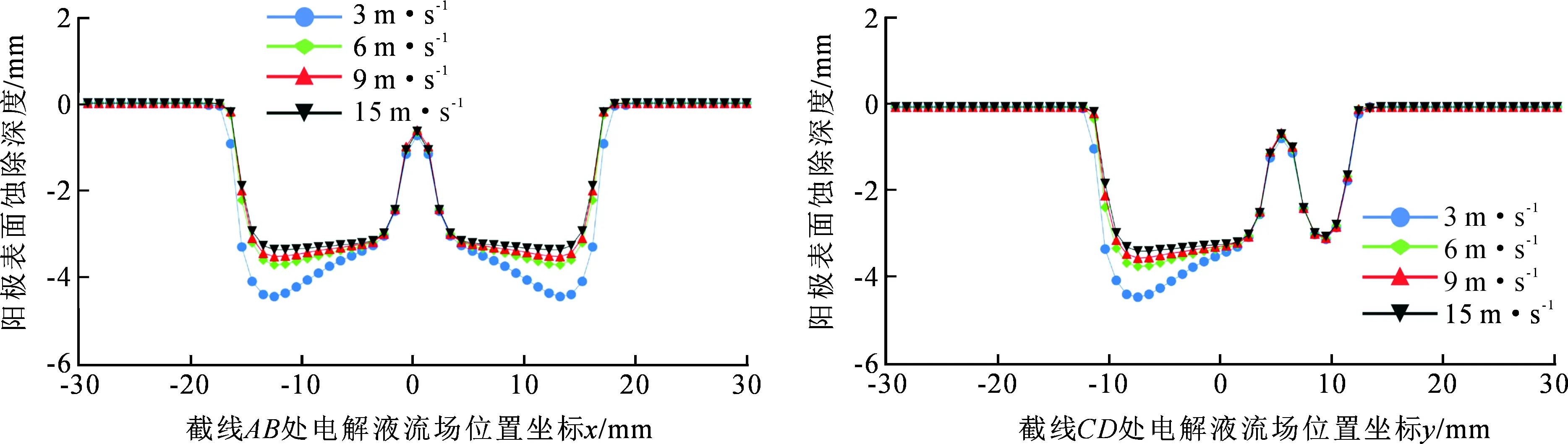
图9 “T”形型腔AB、CD截线形貌

3 结 论

文中电解加工“T”形型腔，建立了基于电场、流场、温度场及结构场的多物理场耦合模型，通过对四种不同入口流速条件下的间隙模型进行仿真计算，得到结论为

1) 当电解液入口流速为6 m·s-1及以上时，间隙内流速均大于5 m·s-1，能够避免钝化现象产生，工件阳极成型形貌精度显著改善。

2) 当入口流速为6 m·s-1及以上时，由于避免了钝化现象的不利影响，间隙内电解液温度相较入口流速为3 m·s-1时显著下降；电解液入口流速越高，间隙内电解液温升越小，当入口流速为15 m·s-1时，间隙内电解液最高温度处在20 ℃～25 ℃之间，满足实际生产中最佳电解液温度分布的要求。

3) 工件阳极表面成型精度和形貌主要受间隙内电流密度分布的影响，电解液温度越高，工件阳极表面电流密度越大，工件阳极表面各位置的蚀除量越大。随着入口流速增加，电解液温升减小，工件阳极表面电流密度分布更加均匀，成型精度有效提高。当入口流速为15 m·s-1时，工件阳极型腔表面精度和形貌尺寸误差较小，成型精度较高。