并联扑翼能量采集与动力学特性的数值模拟研究
2022-08-30王宇璐郭凯伦
王宇璐,韩 影,郭凯伦
(1.咸阳职业技术学院 机电学院,西安 712000;2.西安交通大学 能源与动力工程学院,西安 710049)
作为一种新型清洁能源利用装置,振荡扑翼可实现对风能和海洋能等流场动能的采集和转化,减小火力发电压力,成为近年来备受关注的功率发生装置之一。风能和海洋能属于分散度大、品质较低的流体能,利用扑翼实现对其合理高效地利用是扑翼装置推广应用的关键。
振荡扑翼采集流场能量的过程是通过沉浮运动耦合俯仰运动实现的[1],为获得更高的输出功率和采集效率,需查明控制扑翼运动的主要参数、振荡模式与扑翼采集性能间的内在关系,许多学者基于理论和实验方法对此进行了研究[2-7],结果表明相位差、名义攻角、运动幅值等多项参数都显著影响扑翼的能量采集性能,而最核心的因素是翼型附近涡的形成和发展。文献[8]采用数值计算和可视化实验相结合的方法对扑翼尾缘涡的形成和演变过程展开了研究,查明了缩减频率、俯仰中心等参数对扑翼能量采集过程的影响,分析了涡结构的发展规律。但由于实验条件限制,该研究只对不同影响因素在特殊工况时的性能展开分析,研究结果不足以判断扑翼性能在参数区间内的变化趋势。文献[9]数值模拟了非定常流场中扑翼的沉浮俯仰耦合振荡过程,讨论了无量纲频率在[0,0.25]区间、俯仰振幅在[0,90]区间内超过42个工况下扑翼的采集性能,查明了采集效率在振荡频率、俯仰振幅形成的参数空间内的变化规律,研究还通过两个典型工况证明了翼型厚度、沉浮振幅对扑翼采集效率具有直接影响,但仅仅两个典型工况的结果不能判断其间是否存在采集效率的峰值。一些研究发现通过控制振荡扑翼的运动参数、改变扑翼型线和厚度等[10-13],能一定程度上提升振荡扑翼的能量采集特性。文献[14]等通过构建双自由度分析模型,讨论了常见的四种振荡方式对扑翼非定常水动力性能的影响,解释了振荡形式对流场演变的作用机理。文献[15]针对扑翼在波浪能中的应用,提出了一种以多腔油缸为核心的振荡扑翼波浪能采集装置,采用数值模拟方法对该装置展开结构设计与性能分析,阐明了系统装置性能和设计变量的内在耦合关系。在此基础上,文献[16]等设计并优化了浮式振荡扑翼波浪能采集装置的输出性能,讨论了三种波况下扑翼结构的能量采集性能。然而这些研究只针对单个扑翼进行性能分析,没有涉及多个扑翼同时工作时可能存在的流场相互作用。在实际应用中,为了驱动振荡扑翼、转化并输出扑翼结构采集到的流场能量,需要额外配套相应的扑翼振荡控制装置及能量输出设备,这些设备的造价及维护成本较高,为提高整套装置的经济效益,研究人员考虑在流场中布置多个扑翼同时振荡并采集能量,提高系统输出功率。文献[17]等人提出了一种串联布置的双扑翼水动能采集装置,装置中两个扑翼沿来流方向前后布置,实验证明串联结构的下游扑翼处于上游扑翼的尾缘涡街中,可供下游扑翼采集的流场能量显著减少,直接导致其采集功率和效率相对较低。文献[4,18]的研究同样发现串联结构的下游扑翼采集性能显著受到上游扑翼尾缘涡的影响,其采集效果有所降低。这说明串联结构并不是一个提升扑翼装置整体采集性能的有效途径,为了提升多扑翼装置的输出功率,应保证各个扑翼处在具有相同来流能量的流场环境。
因此,文中提出了一种并联双扑翼结构,基于有限体积法构建并联扑翼数学物理模型,采用动网格技术精确模拟并联扑翼振荡过程,分析了不同沉浮振幅下并联扑翼的能量采集过程,讨论了雷诺数对扑翼能量采集及动力学特性的影响,查明了并联扑翼附近涡结构的演变规律。
1 并联扑翼计算模型
文中以并联布置的两个NACA 0012扑翼为研究对象,两扑翼旋转轴的连线垂直于来流方向,如图1所示。扑翼弦长c设为1 m,图中红框标出的两个扑翼为振荡起始时刻的并联扑翼位置,两者初始间距δ设为1.2 m。图1中点A处为振荡过程中的沉浮极限位置,点B处为振荡过程中的平衡位置。当并联扑翼进行向外冲程运动(即t/T=0~0.5)时,两扑翼分别由其起始位置开始沿箭头所示方向以相反姿态向外振荡,当并联扑翼分别运动到距离其初始位置2H处(即沉浮极限位置)时,向外冲程结束,此时扑翼沉浮速度为0,俯仰速度最大。在t/T=0.5~1.0的振荡周期内,扑翼如图1(b)所示开始向内冲程振荡,最终分别回到初始位置,完成一个振荡周期的运动。
扑翼振荡模式的控制参数包括沉浮振幅H0、沉浮位移h(t)、俯仰振幅θ0及俯仰角α(t)等,如图1所示。研究中选取缩减频率k,其定义如式(1)所示,其中f为扑翼的振荡频率,U∞为来流速度。振荡扑翼采用的沉浮运动和俯仰运动控制方程分别如式(2)和式(3)所示,基于前期的相关研究,文中选取并联扑翼的俯仰振幅θ0为80°[19],俯仰运动旋转轴选取距扑翼前缘1/3倍弦长处,沉浮运动与俯仰运动的相位差选取90°[11]。

图1 并联扑翼运动及参数示意图
(1)
h(t)=H0csin(2πft+φ+β*),
(2)
α(t)=θ0sin(2πft+β*),
(3)
式中:t为扑翼振荡时间;φ为沉浮运动和俯仰运动的相位差。β*为区分两扑翼的参数,当描述上侧扑翼时,取β*=180°,描述下侧扑翼时,取β*=0°。
2 数值分析方法
2.1 数值方法及网格策略
文中的流体为低速空气,为不可压缩黏性流体,其流动规律需满足如式(4)所示的连续性方程以及如式(5)所示的动量方程。式(4)中,ρ为流体密度,u、v、w分别为x、y、z方向的流体介质速度。式(5)中,Fi为控制体受到i方向的体积力,μ为动力黏性系数,Sij为应变率张量。采用软件Fluent 16.0对不同沉浮振幅和雷诺数条件下并联扑翼在流场中的振荡过程进行数值模拟,采用二阶迎风格式对空间项和瞬态项进行离散,通过SIMPLE算法求解离散后的连续性方程和动量方程。
(4)
(5)
为保证计算精度,同时节省计算资源,将计算域划分为如图2所示的内域和外域两部分,内域为边长10c的正方形区域,设置外域边界距翼型表面至少30c[20],以有效避免计算域边界对扑翼表面流动及翼型受力的影响。在并联扑翼表面划分结构化网格,保证扑翼在较大俯仰角度运动时其附近网格不会发生畸变,在除扑翼表面外的内域划分较密的非结构化网格,便于在并联扑翼振荡过程中快速更新高质量计算网格。为减少网格数量,节省计算时间,在外域划分较稀疏的结构化网格。网格形式如图3所示,计算域的网格总数为7.2万。

图2 计算域划分和边界条件

图3 并联扑翼计算网格
并联扑翼的沉浮俯仰耦合振荡过程由动网格技术实现,采用C语言编写用户自定义函数控制并联扑翼的运动轨迹,同时实现实时的网格更新和重构。计算域入口边界设置为速度入口,出口边界设置为压力出口。外域的上下边界设置为移动边界,内域和外域连接处设置交界面边界条件。
2.2 能量采集性能参数
振荡扑翼的耦合运动过程由沉浮运动和俯仰运动两部分组成,扑翼通过振荡运动采集到的流场能量P可由式(6)所示表达式计算为
P=Fy(t)Vy(t)+M(t)ω(t),
(6)
式中:Fy(t) 为y方向扑翼的气动升力/N;Vy(t)为扑翼的沉浮速度;M(t)为扑翼扭矩/N·m;ω(t)为扑翼俯仰速度/rad·s-1。
引入功率系数CP评估扑翼采集到的能量,其表达式为
(7)
其中L为扑翼展向长度/m,文中为二维数值模拟研究,取L为单位展向长度。
扑翼在一个振荡周期内的能量采集性能可由平均功率系数CPm表示,如式(8)所示为
CPm=CPhm+CPθm
(8)
式中:CPhm和CPθm分别为由扑翼沉浮运动和俯仰运动采集到的平均功率系数;T为扑翼振荡周期;Cl和Cm分别为升力系数和扭矩系数。由式(9)和式(10)计算为
(9)
(10)
采集效率η可用于衡量扑翼的能量采集性能。通常以扑翼采集到的功率占扑翼振荡过程扫略面积内的来流总功率的比值来表示η,如式(11)所示为
(11)
其中d为扑翼振荡过程扫略过的垂直高度/m,取d=2H0c[21]。
2.3 无关性验证
为获得正确的数值模拟结果,避免流场域的网格结构和迭代设置对计算结果产生影响,对不同网格划分策略及时间步数下的扑翼振荡过程进行无关性验证。验证工况选取k=1,H0=1.0,θ0=80°,δ=1.2 m的扑翼振荡过程,讨论网格数为5.1万,7.2万,10.8万的三种网格策略,以及一个周期内时间步数为600步,1 200步,2 400步的三种迭代设置。图4展示了不同网格划分策略和时间步数下扑翼在一个振荡周期内的阻力系数Cd和功率系数CP的变化曲线。可以发现,不同方案下Cd曲线的差异很小,且只出现在部分时刻,不同方案下的CP曲线也非常接近,这说明网格数和时间步数的变化对数值模拟结果的影响很小,基本可以忽略。因此,综合考虑计算资源和精度需求,文中选取网格数为7.2万,时间步数为每周期1 200步的数值模拟方案。

图4 不同网格数和时间步方案下Cd和CP曲线
3 数值模拟结果分析
3.1 能量采集特性
振荡扑翼在工程应用时需适应不同的实际运行及流场条件,作为影响流动状态的重要参数,开展雷诺数对并联扑翼能量采集特性影响的研究十分重要。同时,研究考虑扑翼沉浮振幅对并联扑翼振荡过程及性能的影响,讨论了沉浮振幅H0在0.7~1.0间变化时扑翼采集性能的变化规律。图5展示了雷诺数Re为1.1×103,5.0×103,1.0×104以及2.0×104时不同沉浮振幅下并联扑翼的平均功率系数曲线。由图5可知,在多数沉浮振幅下,CPm整体表现出随雷诺数的增大而先减小后平缓的变化趋势。在低雷诺数下,翼型附近流动稳定,有利于涡结构形成和发展,实现能量采集。在中高雷诺数下,雷诺数变化对振荡扑翼能量采集性能的影响程度较小,原因在于雷诺数较大时粘性力的作用小于惯性力,不规则紊流限制了尾缘涡结构的形成,进而降低扑翼功率系数。在相同的雷诺数下,随着扑翼沉浮振幅的逐渐增大,扑翼的能量采集效果显著提升,但其增幅随H0的增大而逐渐减小。由此推测,进一步增大H0对功率系数的提升作用有限。在所研究参数范围内,最大平均功率系数出现在Re=1.1×103,H0=1.0时,CPm=0.81。

图5 不同沉浮振幅及雷诺数下CPm的变化曲线
图6展示了不同沉浮振幅及雷诺数下扑翼采集效率η的变化曲线。由图可知,随着雷诺数的增大,并联扑翼的采集效率整体呈现下降趋势。在相同的雷诺数下,采集效率随H0的增大而呈现先增大后减小的变化规律。这是因为H0越大,扑翼振荡时在垂直方向扫过的高度越大,其扫略面积内的来流总能量越大,但扑翼采集流体能的能力有限,随着H0的增大,扑翼采集到的能量逐渐达到饱和,因此当H0增大到一定程度时,效率η开始下降。最大采集效率出现在Re=5.0×103,H0=0.8时,采集效率为0.44。对于前述最优平均功率系数工况,其并联扑翼的采集效率为0.40,相比最大采集效率有所降低,但扑翼所采集的功率显著增大。实际应用中,在保证较高采集效率的情况下,更高的输出功率能使扑翼装置获得更优的经济效益。

图6 不同沉浮振幅及雷诺数下η的变化曲线
3.2 动力学特性
图7给出了沉浮振幅H0=1.0时,不同雷诺数下升力系数Cl的变化曲线。在一个振荡周期内,不同雷诺数下的Cl曲线整体变化趋势相似,在沉浮极限位置(即t/T=0,t/T=0.5和t/T=1.0时)附近升力系数出现明显波动,这是由翼型表面的涡结构脱落引起的。涡在脱落时,其结构尺寸较大,在涡所处翼型表面形成较大低压区域,在来流作用下导致翼型两侧产生压差,扑翼的气动升力明显增大。整体来说,Re=1.1×103时Cl和Vy的同步性优于Re=2.0×104时,这是前者功率系数较大的原因之一。图8给出了H0=1.0时,不同雷诺数下扭矩系数Cm的变化曲线,可见不同雷诺数下Cm在沉浮极限位置处存在差异,而在平衡位置(t/T=0.25和t/T=0.75)附近时基本一致。这是由于沉浮极限位置处尾缘涡的形成和脱落会引起翼型所受力矩的变化。
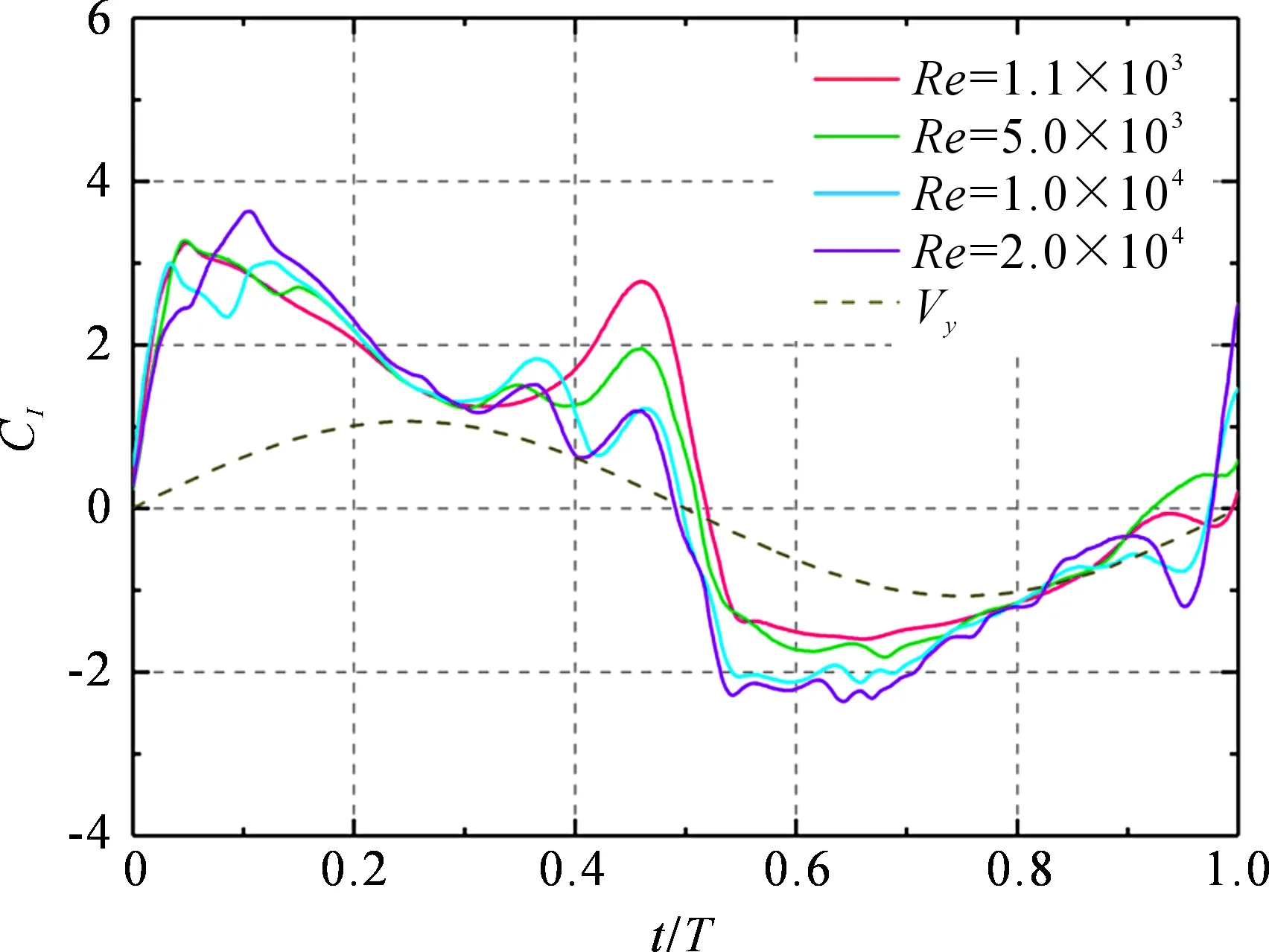
图7 H0=1.0时,不同雷诺数下Cl的变化曲线

图8 H0=1.0时,不同雷诺数下Cm的变化曲线
在并联扑翼进行向外冲程振荡时,扑翼升力系数Cl和扭矩系数Cm的波动范围均显著大于扑翼在向内冲程时的范围。这是因为在进行向外冲程振荡时,两个扑翼相距较近,扑翼尾缘涡脱落时彼此相互作用,在并联扑翼尾部叠加形成了范围较大的低压区域,导致Cl和Cm曲线变化范围更大,而进行向内冲程时两个扑翼相距较远,相互作用弱,对Cl和Cm的影响小。
图9分别展示了H0=1.0,Re=1.1×103和Re=2.0×104时并联扑翼在不同时刻的流场涡量云图。由图9可知,随着并联扑翼向外冲程的进行,翼型吸力面前缘会形成新的涡结构,随着扑翼沉浮俯仰耦合运动的进行,它的尺寸会逐渐增大,并在来流作用下向扑翼尾缘移动,最后形成尾缘涡并发生脱落。对比图9(a)和9(b)可以发现,Re=2.0×104时扑翼在t/T=0.2时刻已经出现前缘涡,相比低雷诺数下前缘涡出现的时刻更早。


图9 H0=1.0时,并联扑翼在不同时刻的涡量云图
对于单扑翼结构而言,尾缘涡发生脱落后会沿着翼型弦线方向向下游运动,而并联扑翼结构改变了涡运动方向,如图9所示。在t/T=0.1时刻,由于俯仰运动使两个扑翼的尾缘相距较近,两个脱落涡相遇,改变原有运动方向,在来流作用下沿水平方向向下游运动。对比不同雷诺数下的流场涡量云图可知,在t/T=0.4时刻,Re=1.1×103时扑翼的尾缘涡尺寸大于Re=2.0×104时的,前者翼型附近的低压区范围更大,翼型两侧压差造成翼型升力系数Cl更大(如图7所示),这是相同沉浮振幅下Re=1.1×103时扑翼平均功率系数更大的原因之一。
4 结 论
1) 文中提出了一种并联扑翼结构,基于有限体积法和动网格技术构建了一套模拟并联扑翼能量采集过程的数值仿真方法,可对多种振荡模式下的并联扑翼能量采集性能及动力学特性展开研究。
2) 并联扑翼能量采集性能的数值模拟分析结果表明,随沉浮振幅的增大,平均功率系数显著提升,采集效率呈先增大后减小的变化趋势。雷诺数对并联扑翼能量采集特性提升作用不显著。最优能量采集性能出现在雷诺数为1.1×103,沉浮振幅为1.0时,最大平均功率系数为0.81。
3) 在动力学特性方面,并联形式使扑翼尾缘涡改变方向,沿水平方向向下游运动。相距较近的脱落涡在翼型尾部形成较大低压区,翼型气动升力和扭矩显著增大。研究发现涡结构尺度显著影响扑翼能量采集性能,后续将进一步讨论复杂振荡模式下涡结构的演变机理及其对扑翼性能的提升作用。
