SD-FCE：一种识别睡眠呼吸暂停综合征发病时段的深度学习方法

高胜寒，熊 馨，相 艳，刘瑞湘，叶哲江

1(昆明理工大学 信息工程与自动化学院，昆明 650500)

2(云南省第二人民医院 临床心理科，昆明 650000)

E-mail：478219759@qq.com

1 引 言

睡眠呼吸暂停综合征(Sleep Apnea Syndrome)是一类最常见的睡眠呼吸系统疾病，包括阻塞型、中枢型、混合型.其主要由上呼吸道部分或完全阻塞引起，临床表现为不同程度的打鼾、口鼻气流基本停止以及心律失常等.在一次8小时左右的睡眠中，呼吸暂停事件会发生数十甚至数百次，严重时会导致一些神经与心脑血管疾病.通常人们使用呼吸暂停低通气指数(AHI)以评估SAS的严重程度，若AHI>5并伴有其他症状的受试者将被诊断为SAS[1-3].

多导睡眠图(Polysomnography，PSG)分析是现今诊断SAS最常用的方法之一，利用患者睡眠期间的生理信号分析其睡眠状态，常用的生理信号包括口鼻气流信号、脑电信号(Electroencephalography，EEG)、心电信号(Electrocardiogram，ECG)等.采集信号的过程要求患者在睡眠时佩戴多个电极帽，之后由睡眠医学专家进行睡眠状态分析.近年来，随着SAS患者的不断增多，睡眠医学专家的严重短缺导致许多患者得不到及时诊断和治疗.因此，有不少研究者进行关于SAS自动检测的研究.Laiali Almazaydeh等人[4]提出了一种基于声音动态检测(Voice Activity Detection，VAD)算法的模型进行特征提取，之后使用分类器进行睡眠呼吸暂停检测.Song等人[5]利用EDR信号和ECG信号中的时域与频域特征，提出一种隐马尔可夫模型用于SAS检测.Sharma等人[6]提出一种基于Hermit基函数从心电信号RR区间提取特征方法，同时使用支持向量机(Support Vector Machine，SVM)进行二分类.M.Emin Tagluk等人[7]提出一种基于双谱分析提取EEG特征的方法进行睡眠呼吸暂停检测.

上述关于SAS自动检测的研究，虽然取得不错的进展，但工作重心还是停留在平均分割信号(传统方法通常将信号分割成30s的数据段)后进行分类，缺少发病的具体时间，无法详细识别发病的中心时间与持续时间，而睡眠呼吸暂停综合症的实际发病情况是一个连续、不确定的过程.传统的分割信号检测机制存在特征信息与检测精度的矛盾，如果每段信号被分得较短，携带的特征信息偏少，影响检测性能，同时需要计算机更高的处理频率；而分割信号较长则导致时间精度下降，检测结果更新缓慢.此外，信号分割还有可能破坏发病时期的连续性，在一定程度上割裂了发病开始、发病时、发病结束存在关联的特征信息.除传统的特征提取与机器学习分类器结合的方法外，近年来，深度学习也为本研究领域注入一些新的思路.卷积神经网络(Convolutional Neural Network，CNN)是一种源自模拟生物视觉信号处理机制的一种深层次神经网络，其结构特征、反向传播以及权值自动更新等机制决定了CNN强大的分析能力.Tao等人[8]提出了一种基于ECG心电信号与LeNet5网络的睡眠呼吸暂停检测模型，通过平均分割心电信号后进行二分类.

由于心肺耦合程度高，心电信号已被广泛应用于睡眠呼吸暂停的检测.受人体内外部病理条件的调节，脑电信号与大脑对神经信息的处理有关.与其它信号相比，脑电信号的产生机制更为复杂，具备更多的神经系统特征信息.例如，当使用功率谱分析脑电信号时，Zhou等人[9]分析了SAS发生之前、期间和之后睡眠脑电信号变化.当SAS发生时，EEG的绝对功率和相对功率在0～15Hz频段存在升高，在15～30Hz频段较SAS发病前降低.而在SAS发病后，各频段的绝对功率均显著高于SAS前，但在0～8Hz频段的绝对功率有所恢复.SAS发病时睡眠脑电信号的变化为利用睡眠脑电信号检测SAS提供了支持，这些更全面的特征在其他PSG信号中是不存在的.脑电信号的研究频段主要集中在0-30Hz，依据睡眠状态与脑电信号的医学原理与特征，可将脑电信号分为以下几种节律波：1)δ波：0.5～3Hz；2)θ波：4～8Hz之间；3)α波：8～13Hz；4)β波：14～30Hz.

睡眠呼吸暂停综合征检测的难点在于特征提取与发病时间的确定.大脑功能连接性的衡量方法包括脑电信号通道间的相干性、相关性、锁相值分析、相位滞后指数等，利用来自两个通道或不同大脑区域的EEG信号之间的线性相关作用，如果两个信号之间存在较高的一致性意味着存在同步的神经元活动、神经元功能整合，反之低一致性则意味着存在独立活动的神经元，此时神经元功能存在分离[10-12].Li[13]等人在进行神经系统异常组与健康组对照实验中观察到大脑功能连接性的差异.利用脑电功能连接性来研究神经系统类疾病已取得一定成功，通过对 EEG 信号构建脑网络并进行量化分析，能在临床上辅助睡眠呼吸暂停综合症的诊断[14].

针对目前SAS自动检测机制的不足，本文基于睡眠脑电信号，利用脑电功能连接性与改进目标检测算法[15，16]提出一种新的SAS自动检测模型SD-FCE(SAS Detection based on Functional Connectivity of Electroencephalography)，其主要包含以下几个方面：

1)在EEG的预处理中，引入经验模态分解(Empirical Mode Decomposition，EMD)[17，18]进行分解-去噪-重构，以降低EEG中噪声的影响.同时为了避免特征信息的割裂，确保每一次发病的EEG信号完整性，本文通过较长的固定滑动窗口与相对较短的滑动步进从EEG中提取数据片段进行分析，保证每次检测模型获得足够的特征信息；

2)利用神经系统异常时所产生的脑电功能连接异常作为主要特征构建脑电功能连接矩阵，之后将功能连接矩阵输入卷积神经网络以完成特征提取；

3)模型包含两个用于识别SAS是否发病和发病时中心时间、持续时间的模块.为同时进行合理的优化，本文模型的损失函数综合了分类与回归，标签中负样本的位置数据不参与损失的计算，一定程度缓解样本不均衡所带来的影响.

相比于传统的二分类算法，本文从SAS发病的神经功能特征入手，基于SSD目标检测算法的改进，从根本上改变了SAS的检测机制.直接检测发病的中心时间点与持续时间将更加接近于真实情况，同时性能优于其他基于EEG的目标检测[19，20]模型.

2 SD-FCE模型

2.1 数据提取与标签匹配

本文通过固定滑动窗口从EEG中提取数据片段进行处理.在单次检测过程中，一段时间长为120s的睡眠脑电信号被视为检测载体的最小单位xn∈X(n∈N*)，xn通过长度为120s的滑动窗口从某位受试者8小时左右的睡眠脑电信号X中提取.选择长度120s、步进10s的滑动窗口为了尽可能的使检测载体的最小单位xn能够完整的包含发病时间相对较长的目标，同时选择步进较小的滑动机制是为了应对发病位置的不确定性，如图1(a)所示.

图1 EEG片段提取(a)、预选框与真实发病框的表征(b)、重叠度(c)Fig.1 Extract EEG segments(a)，representation of default frame and true frame(b)，intersection over union(c)

基于滑动窗口提取到的数据段，以每z秒为一个中心时间点生成一系列用于密集采样的预选框(Default frames)，这些预选框的长度从10s～120s均匀增加，步进为10s.若z=1时，则每段数据上将生成Nd=12×120s=1440个预选框，若z不确定，则每段数据上将生成Nd=1440/z个预选框.单个预选框定义为Di={ci，di}(i∈[1，Nd])，其中ci与di分别为预选框的中心时间点与持续时间，如图1(b)所示.同理，将呼吸暂停实际发病的时间位置信息用真实发病框(True frames)表征为Tj={cj，dj}.

在训练开始之前，需要将预选框与真实发病框进行匹配，匹配后得到真实发病框相对于预选框的偏移值.设偏移Oi={Ci，Di}，则由公式(1)即可得到匹配后的偏移值.

(1)

此举在于将每段数据对应的发病情况进行网格化整理与位置数据归一化.例如，一些数据段存在着不同数量、时间长短不一的发病片段，而其余数据不存在发病，这种随机性将导致难以直接使用未处理的真实发病框.在训练与测试过程中，网络对于目标位置信息的输出O′i={C′i，D′i}就是被预测的真实目标相对于已知预选框的偏移值.匹配的原则包括以下几个方面：

1)单个真实发病框能匹配多个预选框，反之则不能；

2)决定两者之间是否匹配的参数是重叠度(IoU)[21].IoU定义为两者交集与并集的比值，如图1(c)所示.只有IoU值大于匹配的阈值才可进行匹配，即IoU{Di，Tj}>μ，其中IoU，μ∈[0，1].若出现某一个预选框与多个真实发病框均大于匹配阈值，那么将选择IoU值最高的真实发病框与其完成匹配.事实上，匹配阈值设定合理的前提下，上述情况非常少见；

3)对于匹配阈值的设置，为了尽可能降低正负样本不平衡所带来的影响，同时考虑任务的类型，我们需要使网络对预选框的正向预测倾向于保守.这是因为对于模型的预测结果还需进行非极大值抑制(Non-Maximum Suppression，NMS)[15]处理，以消除一些正向预选框同时识别同一个目标，仅留下正向预测概率最大的一个预选框，所以不需要训练数据处于绝对平衡的二分类情况之下.通过相关研究[19-23]，设置匹配阈值将正负样本的比例控制在1：3左右能取得相对更好的效果.

4)将匹配成功的预选框标记为正样本，对应位置信息为得到的偏移值；其余则标记为负样本，位置信息均为0.

在完成匹配之后，得到经过处理的标签li={Ci，Di，Gi，Si}，其中Gi与Si分别为背景信号与SAS发病的分类标签，且有Si，Gi∈{0，1}.

2.2 脑电功能连接性分析

2.2.1 相干性分析

相干性用于分析信号之间的频谱互相关，其数学表达式如公式(2)所示：

(2)

其中n为每段信号的数据点数，A和φ分别为信号的振幅和相位，分子表示在频率f下信号x和y之间的交叉谱密度，分母表示频率f下信号x和y功率估计乘积的平方根.在频率f0处，Cohxy(f0)的值介于0～1之间，其中0表示无耦合，1表示两个信号之间的最大线性相关.

2.2.2 相关性分析

相关性用于估计信号间时域内的线性相关的水平.

(3)

如公式(3)所示，Cov(x，y)是信号x和y之间的协方差，σx和σy分别是信号x和y的标准差.并且存在Corrxy∈[-1，1]，当Corrxy=±1时，信号间呈现正或负线性相关性；当Corrxy=0时，信号间无相关性.

2.2.3 锁相值分析

锁相值分析(Phase Locked Value，PLV)是利用相位同步来分析信号之间可能存在的功能性相互作用.当公式(2)中的Ax(f，k)=Ay(f，k)=1时，可得到PLV的表达式如公式(4)所示：

(4)

在频率f0处存在PLVxy(f0)∈[0，1]，当PLVxy(f0)=0时，信号间缺乏相位同步；当PLVxy(f0)=1时，信号间完全相位同步.

2.2.4 相位滞后指数分析

相位滞后指数(Phase Lag Index，PLI)表示信号之间相位差分布的不对称性，其定义如公式(5)所示：

(5)

式(5)中，n为信号通道的长度，φx(f，k)-φy(f，k)表示频率f下信号x与y之间的相位同步.在频率f0处存在PLIxy(f0)∈[0，1]，当PLIxy(f0)=0时，信号间没有耦合；当PLIxy(f0)=1时，信号间完全耦合.

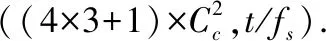
2.3 SD-FCE模型结构

SD-FCE模型主要由特征提取模块φT、分类模块φC、位置回归模块φL共3个部分构成.φT模块主要包含脑电功能连接性特征提取与卷积神经网络的部分层组，经过数据提取与预处理的EEG信号两两通道间进行脑电功能连接性分析，得到脑电功能连接矩阵.随后将脑电功能矩阵输入卷积神经网络的层组，其主要包含k个大致相同并且依次相连的结构，每个层组均包含卷积层、最大池化、批标准化、RELU激活函数.经过特征提取后得到的特征向量将进入分类模块φC与位置回归模块φL.SD-FCE模型的结构如图2所示.

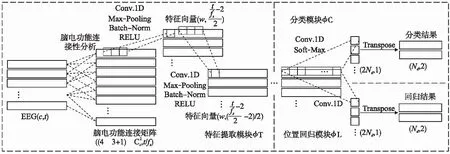
图2 SD-FCE模型的结构Fig.2 Architecture of SD-FCE

若输入的EEG通道数为c、每个通道的数据点数为t，卷积神经网络宽度为w，φT模块中第k组卷积神经网络特征提取层的输入数据点数为tk，每段数据上生成Nd个预选框，模型参数如表1所示.

表1 模型参数Table 1 Model parameters

φC与φL模块均包含一个相同的卷积层，其使用与特征向量等长的卷积核(kernel)进行处理，但网络宽度(width)不再与φT相同，为了模型能按预选框的数量输出对应的分类与位置回归结果，将网络宽度设置为两倍于每段数据上生成的预选框数量.φC与φL模块不同的是分类模块φC多出一个Soft-max层，为了将分类的输出划归为类别预测概率.

2.4 损失函数

损失函数(Loss function)是一类用于衡量预估事件与真实事件差别的函数，通常作为模型的优化准则，通过寻求损失函数最小化进行优化.在SD-FCE模型中，损失函数L(p(xi)，li)建立在模型预测值p(xi)={C′i，D′i，G′i，S′i}与真实标签li之间，G′i与S′i分别为模型对背景信号、SAS发病的概率，且有G′i，S′i∈[0，1].令∑L(p(xi)，li)=φ++φ-，其中φ+与φ-的值分别如公式(6)、公式(7)所示:

(6)

(7)

(8)

公式(6)、公式(7)中m+与m-分别为某一批次训练标签中正、负样本的个数.将损失以正、负样本分开计算后除以其样本个数，并且在负样本中不计算位置信息的损失，此举有利于缓解数据的不平衡性，同时尽可能降低背景信号位置标签所带来的影响.L1smooth(Δx)损失函数源自Fast R-CNN[21]中计算目标回归框的损失，本文中我们将其用于计算正样本位置信息的损失，详见公式(8).

2.5 预 测

为了使不规律的真实发病框网格参数化，需要利用规则的预选框对其进行匹配，模型依托于规则的预选框输出相应的偏移量.在预测时，输出的偏移量需要与其对应的预选框位置数据进行解匹配，即逆向计算公式(1)才能得到实际预测的SAS发病位置.实际情况中，由于匹配时存在多个预选框均匹配了同一个真实发病框，所以在预测时也存在多个预选框同时预测一个SAS事件.对此，在解匹配之前，还需要通过非极大值抑制[15]对预选框进行筛选，仅留下一个预测分数最高的预选框用于解匹配得到真实预测的SAS事件.在非极大值抑制中，首先将这些预选框按预测分数由高到低排序，然后将分数最高的预选框依次与第2名、第3名等进行IoU计算，如果IoU值高于一定阈值，则视为它和分数最高的预选框预测的是同一个SAS事件，将其删除，直至剩下最后一个分数最高的预选框.依次计算IoU的过程是为了排除那些与分数最高的预选框重叠度不高的其它预选框，因为同一组数据有可能存在预测其它SAS的预选框.

3 实 验

3.1 数据集

本文实验数据来自由葡萄牙克英布拉大学(Universidad de Coimbra)睡眠医学中心采集并公开的多导睡眠图(Polysomnography，PSG)数据集“ISRUC-Sleep”[24].数据集共包含3个数据子组(Subgroup I、II、III)，分别为睡眠障碍受试者100例、服用睡眠药物的受试者8例以及健康受试者10例.每位受试者的PSG均由完整的8小时左右睡眠行为构成，大部分PSG提供了18个通道，其中有6个通道为睡眠EEG(F3-A2、C3-A2、O1-A2、F4-A1、C4-A1、O2-A1)，采样频率200Hz，两个通道为呼吸气流，采样频率12.5Hz.数据集提供了每位受试者包括年龄、性别、其他病症、药物服用情况在内的基本体征信息，以及由两名训练有素的睡眠医学专家进行睡眠分期、睡眠事件、SAS发病情况的标记.

数据集提供了睡眠障碍受试者单位时间段内是否发生SAS的标签，结合PSG内提供的呼吸气流通道可得到受试者发病的具体时间信息[7]，如图3所示.

图3 SAS发病的时间段[7]Fig.3 Case of SAS time [7]

本文使用了Subgroup I中仅患SAS的睡眠障碍受试者PSG数据共计12名，表2统计了每位受试者在一次完整的PSG采集中SAS的发病次数、最短与最长的持续时间以及平均持续时间.选取的12名受试者的睡眠EEG经过预处理后得到18485组包含6通道、每通道长度为24000的数据与其对应的分类、位置标签.表3统计了包含一定目标数量的数据组数.

表2 受试者的SAS发病信息Table 2 SAS information of subjects

表3 包含一定目标数量的数据组数Table 3 Quantity of EEG segments with number of SAS

3.2 数据预处理

EEG以其信号微弱、极易混入噪声等特性为研究人员带来许多挑战.传统的EEG预处理包括使用一个频带宽度为0-35Hz左右的低通滤波器进行滤波，以此来滤除EEG中的高频噪声.但由于EEG是典型的非线性、非平稳信号，傅里叶变换以其固定的基函数为非平稳信号的分析带来一定的局限性.Norden E.Huang等人[17]提出一种新的处理非平稳信号的方法——经验模态分解(Empirical Mode Decomposition，EMD)，EMD可以依据数据自身的时间尺度特征来进行信号分解，无须预先设定基函数.这与建立在需要基函数的傅里叶变换、小波变换方法有着本质区别，因而EMD在处理非平稳及非线性数据上具有非常明显的优势，利用其自适应性进分解-降噪-重构能获得更为纯净的EEG信号.

数据集提供的睡眠EEG为未经过任何处理的原始EEG，一些片段不可避免的混入了噪声，如果不能合理地削弱这些噪声，低质量数据将会使模型学习受到极大的干扰.在本文处理过程中，结合数据集的实际情况，采用两种方法对数据进行清洗：

1)将受噪声污染严重的片段删除；

2)使用EMD对其进行分解、降噪、重构操作，以去除高频噪声.将每段数据进行EMD分解得到9-14不等个IMFs分量，由于EEG中含有的噪声基本处于高频部分，所以将最高频率的IMF分量去除，剩下的IMFs分量进行重构获得降噪后的信号.原始EEG信号与降噪后的信号如图4所示.

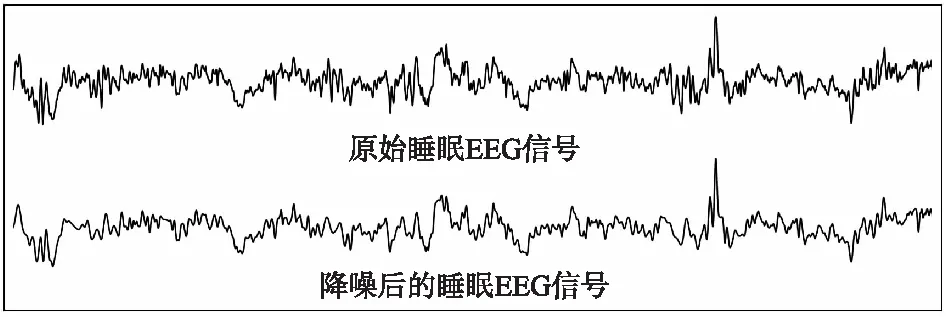
图4 原始EEG与降噪后的EEG时域对比Fig.4 Raw EEG and de-noised EEG in time domain

3.3 实验环境

本文实验操作的环境为Ubuntu 18.04.3LTS操作系统、Inter Core i5 8250U、16GB RAM、Python3.7.3、Pytorch1.2.0.实验超参数设置如表4所示.

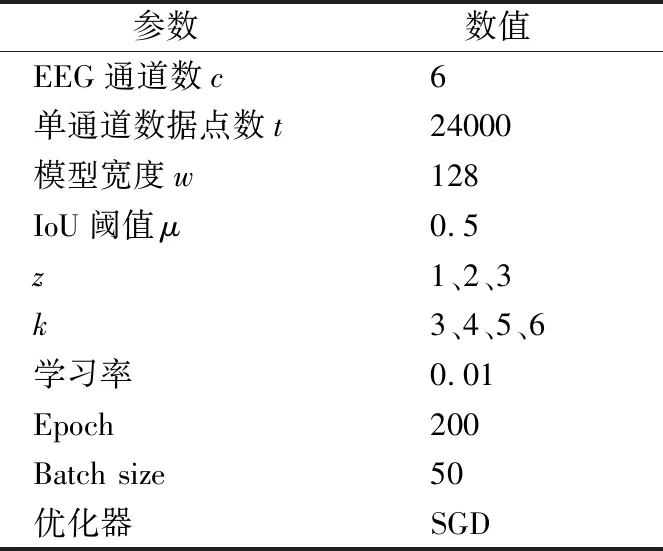
表4 超参数设置Table 4 Hyper-parameters settings

本文采用召回率(Recall)、精确率(Precision)、F1-score、最小二乘估计(Least Square Estimate，LSE)作为评价指标，设TP，FN，FP，TN分别为真阳性(True Positive)、假阴性(False Negative)、假阳性(False Positive)、真阴性(True Negative)，那么召回率、精确率、F1-score、LSE分别如公式(9)-公式(12)所示.

(9)

(10)

(11)

LSE=∑(yi-y′i)2

(12)

4 实验结果与分析

4.1 实验结果

在超参数设置中，k的取值直接决定了网络的规模大小，本文通过对近年来相关论文的研究[19，20，25-27]，在一定范围内没有发现网络规模与性能存在直接且固定的联系，所以本文设置了一组对照试验，将k分别取值为3、4、5、6，以验证不同网络规模对于网络性能的影响.对于本文的方法，z的取值也至关重要，这将直接影响网络对于位置预测的精度与网络的规模.依据得到Nd值的大小，本文将z分别取值为1、2、3，与此对应的Nd值分别为1440、720、480.对照实验的结果如表5所示.

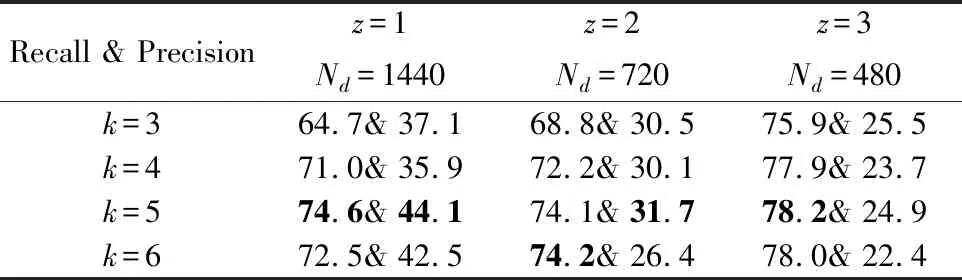
表5 网络深度与预选框数量的实验结果对比Table 5 Experimental results of network depth and number of default frames

通过对比实验，随着网络层数的加深，召回率(Recall)有一定程度的上升，但由此带来的影响就是精确率(Precision)下降.同时随着预选框生成的数量减少，也出现了召回率上升、精确率下降的结果，因此考虑模型回归的精度与模型复杂度，最终选择k=5、z=1.

为验证本文模型的性能，本文进行了多次实验，对比S.Chambon等人[20]提出的DOSED(Dreem One Shot Event Detector)检测模型与其对比实验结果，其对比模型包括Parekh等人[28]与Lachner-Piza等人[29]提出的模型.上述对比模型在SSC(Stanford Sleep Cohort)[30]数据集进行了实验，对比本文模型的实验结果如表6所示.模型的ROC曲线如图5所示，模型训练时的损失曲线如图6所示.

图5 ROC曲线Fig.5 ROC curve

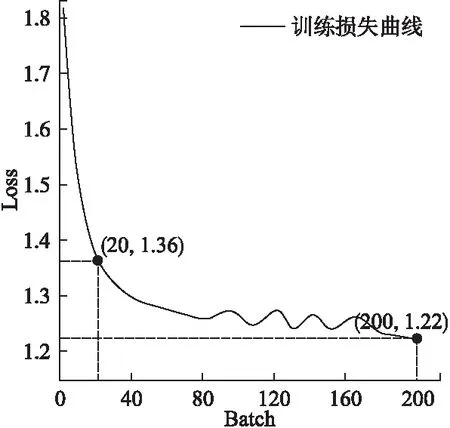
图6 损失曲线Fig.6 Loss curve

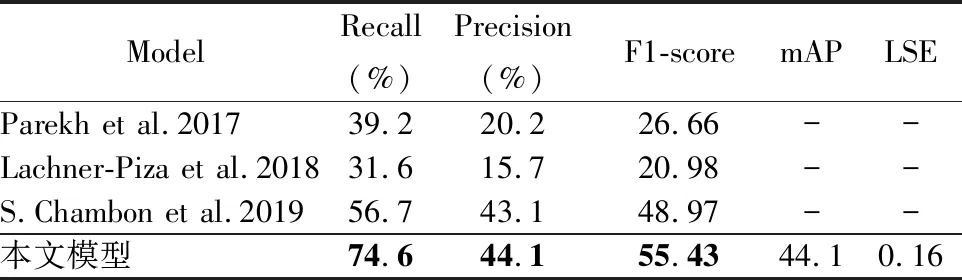
表6 实验结果Table 6 Experimental results

4.2 实验结果分析

通过实验结果可以发现，本文模型的性能在平均召回率(Recall)、平均精确率(Precision)方面优于以往提出的基于EEG的检测任务.睡眠K-复合波(K-compose)、纺锤波(Spindle)与频带能量是EEG的主要特征，而SAS发病时间段与正常睡眠时间段的结合部分与K-复合波存在一定的关系，正常偏深睡眠时期下丘脑会产生一些纺锤波，睡眠的深浅与SAS发病时存在一定的关联，但K-复合波的产生并不一定是由于SAS发病产生的，所以网络对特征较为明显的K-复合波存在一定的误判概率，除了对多个正向的预选框正确预测之外，还可能存在一些零散的负样本被错误地预测为正向，所以模型的结果相对于类似的任务对一些数据存在“选择性”.

与传统的均匀分割后进行二分类的SAS检测任务不同，传统的检测任务经过特征提取与分类之后仅需要预测两个数值，而在网络规模相差不大的情况下本文提出的方法需要输出1440×4个数值，这使得结果包含很多不确定性.但预测时并不是这1440个预选框的数据都有用，我们只需要那些相对来说评分较高、多个正向且重叠度较高的预选框，一些单独存在于其他地方的正向预选框可以忽视，这是因为检测方法中使用了大量的预选框进行密集采样，某一个被检测的目标将会被多个预选框集中识别.最后通过非极大值抑制，留下一定范围内评分最高的预选框与其对应的偏移量，解匹配得到真实的预测位置数据.

实验结果表明，本文提出的全新SAS检测模型具备可行性，同时模型性能优于其他EEG目标检测任务.

5 讨 论

本文提出了一种全新的检测SAS方法，通过脑电功能连接性分析与卷积神经网络为主要的模型结构完成特征提取、分类与位置预测.相比于传统SAS检测方法与EEG类似的研究，该方法不再局限于平均分割信号后进行分类，而是在一定时间段内预测每次发病的时段，因为SAS发病的时长与时间点对于医生的诊断也蕴含着非常重要的信息.为了使模型在学习预测中受干扰更小、更容易学习到特征，本文提出EMD等方法进行信号去噪声、去伪迹；使用特定的滑动窗口数据提取机制，既提高了检测频率，同时也保证模型单次预测可用的数据量足够多，以获得更好的结果.如何处理不规则的发病时间标签是本文的关键一步.参考目标检测算法的过程，使用类似的用于密集采样的预选框将真实的发病时间标签网格参数化.特定的损失函数保证了分类与回归的同时优化.针对两个分别用于分类与位置预测的模块，损失函数进行了功能区分，并且一部分预测结果不参与损失函数的计算.正样本同时参与分类、回归的损失计算，负样本则仅参与分类的损失计算，以减轻数据不平衡所带来的影响.

分析睡眠EEG是诊断SAS的重要途径之一.睡眠EEG不仅提供了整体睡眠结构与睡眠状态的宏观信息，还提供了时域中的微观结构.Alattar M.A等人[31]的研究表明，SAS患者睡眠期间的觉醒与呼吸暂停事件对皮层脑电影响显著，这决定了SAS患者的睡眠脑电在微观结构中存在异于健康人的部分，特别是CAP活动.CAP(Cyclic Alternating Pattern)[32]是一种涉及大脑皮层的一种脑电活动，常出现于睡眠的NREM期.CAP活动由A相与B相组成，A相由一段主要成分包括慢波(Slow waves)、Detal波、K-复合波等高振幅波构成，而B相为普通的背景节律波，以A相+B相组合为一次CAP循环.SAS严重干扰睡眠结构与稳态，而CAP作为睡眠稳态的标志，将直接导致睡眠EEG的微观结构发生一些特定的变化[32-34].

本文利用SAS发病时神经系统异常特征与深度学习方法，以SSD目标检测算法为基础提出一种新的SD-FCE模型，为SAS自动检测提供了新的思路与可靠的自动检测结果，该方法的提出为医生在SAS临床诊断中提供了更多的重要信息，这是传统分类方法所不具备的绝对优势.在下一步的研究中，本文将继续寻求模型改进方法，包括尝试不同的网络结构、关注最新的相关算法，挖掘脑电内更多维度的特征，以获得更佳的性能.