深度学习几何约束预测的蛋白质建模方法

杨 涛，刘 栋，刘 俊，张贵军

(浙江工业大学 信息工程学院，杭州 310023)

E-mail：zgj@zjut.edu.cn

1 引 言

蛋白质是由氨基酸脱水缩合形成的生物大分子，是生命活动的主要承担者，其空间结构决定了其特定的生物学功能[1].获取蛋白质结构，对蛋白质功能注释、疾病研究、靶标药物的设计有重要研究价值[2，3].蛋白质结构预测是结构生物信息学中一个尚未解决的重要问题.目前，获取蛋白质结构的主要方式还是X射线晶体衍射、核磁共振和冷冻电镜等生物实验方法，但时间成本和资金成本都很高[4，5].Anfinsen的研究表明蛋白质的氨基酸序列决定了其空间结构，蛋白质的最终折叠结构是最低自由能构象，这给蛋白质结构预测提供了理论基础[6].根据Anfinsen准则，从氨基酸序列出发，通过蛋白质物理与知识能量模型，利用计算机技术结合优化算法，探索蛋白质构象空间最优解的从头预测方法已成为生物信息学领域的研究热点[7].由于基因测序技术的快速发展，当所研究的蛋白质有大量同源序列时，通过直接耦合分析(DCA)[8-10]技术能够推断长程残基接触，得分高的残基对接触足够准确且分布良好，能有效的辅助蛋白质折叠.根据两年一次的蛋白质结构预测关键评估(CASP)[11]实验准则，如果蛋白质序列中两个残基Cβ原子(没有Cβ原子，用Cα代替)之间的欧式距离小于8Å(其中Å为Angstrom，表示0.1纳米，常用于原子间距离描述)，定义为接触.2012年，深度信念网络[12，13]被Cheng团队尝试用于预测蛋白质残基间接触辅助蛋白质三维结构建模，自此深度学习方法在蛋白质结构预测领域大放异彩.之后，Xu团队引入全新的接触预测模式(同时预测一个区域里面的所有接触而不是一个接触)和新的深度网络体系架构ResNet[14].深度残差网络应用于蛋白质残基间接触预测使蛋白质结构建模取得了重大进展[15，16]，利用预测的残基间接触来辅助蛋白质结构建模方法主要分为两大类：第1类是基于片段的方法，例如Rosetta[17]、QUARK[18]和CGLFold[19]，将深度学习预测的残基间接触转化为约束添加到片段组装[20，21]方法中.基于片段的方法在CASP实验中表现良好，但需要大量的计算能力，依赖于可用的天然态片段产生不同分数的类似天然态模型.对于复杂的β片层拓扑结构，尤其是那些高接触的拓扑结构，片段组装方法通常不能产生高精度的模型[22].另一类是基于几何约束的能量极小化方法，近几年大放异彩，其中CONFOLD2[23]将预测的接触约束转化为标准原子间距离约束，使用晶体学和核磁共振系统CNS(Crystallography & NMR System)[24]套件从这些约束中生成坐标折叠蛋白质结构.CONFOLD2在两阶段建模方法中集成了二级结构和预测的接触，在初始模型生成后过滤掉不精确的预测接触.当没有大量足够精确的接触，产生的蛋白质模型很差[25].

在最近的研究中，基于深度学习预测残基间距离分布应用于蛋白质结构预测问题，使得在蛋白质数据库中缺乏同源模板的蛋白质直接从序列折叠精确的三维结构成为可能.DeepMind开发的AlphaFold[26]表明，残基间距离可以通过深度学习从协同进化数据中准确预测，采用深度残差网络预测残基间距离分布，并将其转化为蛋白质特异性的距离势能，通过采样和梯度下降算法优化距离势能，生成蛋白质结构.RaportX利用ResNet预测原子间距离分布，将其转换为平均距离和偏差，并以此作为距离边界，由CNS构建蛋白质三维结构[27].IPTDFold利用局部二面角交叉变异广泛探索构象空间，构建基于残基间距离约束的loop区域二面角模型，通过差分进化算法得到满足约束的旋转角；最后，根据构象和预测距离之间的差异评估残基距离偏差，并引导概率有偏的残基二面角优化[28].这些方法极大促进了蛋白质结构预测领域的发展.

本文开发了GCPFold方法，设计了深度残差网络预测残基间的距离分布，深度残差网络和长短时记忆网络预测蛋白质主干二面角分布，并开发了基于能量极小化的优化方法，利用预测的残基间二面角分布转化为均值，通过加入扰动方式引入随机效应产生不同的初始二面角，使用预测的距离分布转化为能量势能，利用Rosetta能量函数来补充预测的约束，指导蛋白质折叠.GCPFold只需要在标准的计算机上运行一个小时左右，就可以完成蛋白质的结构预测.

2 方 法

2.1 构建数据集

为了训练用于预测残基间距离和主干二面角的神经网络，从SCOPe[29]中构建了6791个蛋白质单域数据集.如图 1(a)所示，基于PDB库蛋白质的序列记录，所有SCOPe2.07序列共计244735条.使用CD-HIT序列聚类工具[30]，以30%的序列相似度聚类去冗余得到10569个蛋白质，提取分辨率小于2.5Å、长度在30～300之间的序列，构成包含6791条序列的数据集，为数据集中的每一条序列搜索多序列比对(MSA).如图 1(b)所示，设置HHblits[31]的E-value阈值0.001，序列最大相似度99%，查询序列覆盖率(对齐的残基数目和查询序列长度的比值)50%，在Uniclust30数据库[32]迭代3次搜索MSA，如果MSA中有效序列条数小于100条，利用Jackhmmer[33]在UniRef90[34]数据库进一步搜索，得到最终的MSA.将数据集中的6711蛋白质用于网络的训练和验证，80个蛋白质作为独立的测试集.这80个测试蛋白的折叠类型包括α、β和α/β，这些蛋白质的三维结构已由生物实验测定，且被广泛用于蛋白质实验测试[35，36]，可以测试GCPFold的性能.

图1 构建数据集和搜索MSAFig.1 Build data set and search MSA

2.2 基于MSA提取特征集合

序列权重：在多序列比对中相似度高的序列减小权重，相似度低的序列增加权重.根据经验设置序列相似度阈值为75%，第m条序列的权重如公式(1)所示：

(1)

多序列比对中有效序列数Wsum如公式(2)所示：

(2)

其中Wm表示第m条序列的权重，N表示多序列比对中序列条数.

2.2.1 序列频率谱

序列频率谱表示多序列比对中每列氨基酸的分布情况，可以反映序列进化的趋势.目标序列的第i位置处频率如公式(3)所示：

(3)

2.2.2 位置熵

序列i位置的熵表示多序列比对中第i列残基分布随机性的度量，计算方法是该列中每个残基出现频率与对数频率值乘积之和，如公式(4)所示：

(4)

其特征维度为1×L.

2.2.3 协方差矩阵

在概率论和统计学中，协方差用于衡量两个变量之间的总体误差，引入到生物信息学领域，协方差特征衡量了蛋白质序列中不同位置之间的边际关系，由多序列比对中给定位点的残基频率和残基对频率计算得到.其中残基对频率，对于输入MSA中的每一对列，计算观察到每对列出现20种标准氨基酸的概率，将gap是视为额外的氨基酸类别，未观察到的残基对的频率用伪计数1来表示，如公式(5)所示：

(5)

协方差矩阵如公式(6)所示：

Covij(A，B)=fij(A，B)-fi(A)fj(B)

(6)

其特征维度为441×L×L.

2.2.4 CCMpred计算的耦合分数

由于协方差矩阵只能捕捉变量之间的边际关系，没有消除间接耦合噪声的存在.如果蛋白质空间结构上残基A、残基B均与残基C接触，即使残基A与残基B非接触，它们也表现为协同进化关系.引入CCMpred[37]计算的耦合分数来消除间接耦合的噪声，通过使用马尔可夫随机场学习MSA的生成模型来消除观察到的相互作用网络中的传递相互作用.其特征维度为1×L×L.

2.2.5 残基对接触势能

研究发现一些氨基酸具有隐藏在蛋白质内部的趋势，基于此估计疏水作用的经验值，一些氨基酸倾向形成相互作用的残基对[38-40].基于这些先验知识，MR.Betancourt等人给出相互作用矩阵B[41]，提供了与实验非常一致的疏水性.基于相互作用力矩阵B计算残基间势能ConPot，如公式(7)所示：

(7)

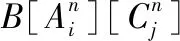
2.2.6 互信息

互信息(MI)衡量一个位置对另一个位置的依赖性[42].在多序列比对中识别相关突变的最常用方法是计算两个位点之间的MI.第i列和第j列残基间的互信息是指在明确第i位置的残基类型A后，第j位置的残基类型B的信息减少量.如公式(8)所示：

(8)

其特征维度为1×L×L.

2.2.7 去除背景噪声的互信息

蛋白质家族进化过程中的补偿性改变会产生包含重要结构和功能信息的共同进化位置.由随机噪声和系统发育成分组成的背景信息干扰了共进化位置的识别.S.D.Dunn等人准确估计给定蛋白质家族中每对位置的背景互信息水平，去除此背景信息会产生一个度量标准MIp，可正确识别蛋白质家族中更多的共进化位置[43].MIp如公式(10)所示：

(9)

MIp(A，B)=MI(A，B)-APC(A，B)

(10)

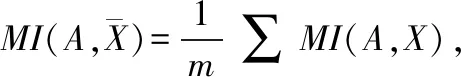
2.3 标签数据

对数据集中的蛋白质，根据序列残基中Cβ原子三维空间坐标，计算每对残基间的欧式距离和相邻残基间二面角.如果残基中不包含Cβ原子，以Cα原子代替.根据残基间的欧式距离，以0.5Å为间隔将2Å～20Å分成36个距离区间，分别标记为1～36，在2Å～20Å之外作为第37个距离区间，标记为0.残基间二面角在[-180°，180°]之间，以15°离散为24个角度区间，分别标记为0～23.用于训练过程根据交叉熵损失函数计算损失.

2.4 网络架构

与传统的卷积网络相比，残差网络易优化.通过增加网络层数迭代训练学习更佳的参数来获得更高的预测精度.这类模型在图像识别领域应用广泛，在生物信息学领域预测蛋白质残基间几何信息也有很好性能.本方法从多序列比对中提取蛋白质序列的一维和二维特征，输入到基于PyTorch框架搭建的神经网络中预测残基间距离和相邻残基间二面角.

如图2所示，设计残差神经网络用于预测残基间距离.从多序列比对中计算序列频率谱、位置熵，残基间协方差矩阵、CCMpred计算的耦合分数、接触势能、互信息和去除背景噪声的互信息.如图 3所示，对定义在单个残基上的特征通过水平和垂直条带化扩维，与定义在残基对的特征组合成489×L×L特征张量.输入到二维最大池化层进行降维，得到64×L×L的特征张量.通过二维实例归一化层对特征数据进行规范化处理，输入具有膨胀系数的32个残差块中.前30个残差块膨胀系数是1、2、4、8、16的循环，最后两个残差块膨胀系数为分别是1、1.所有的残差块均由一个二维卷积层接收来自上一个残差块的输出，经过实例归一化层和Relu激活函数之后，利用二维Dropout层进行随机丢弃避免过拟合，Dropout rate设置为0.25，再经过一个二维卷积层和实例归一化层之后通过跳跃连接与残差块的输入累加到最后Relu函数上，作为下一个残差块输入.模型的输出层在32个残差块之后，由一个1×1的Fliter的二维卷积层和一个Softmax函数组成，根据残基间距离离散的37个距离区间，输出每对残基落入各个距离区间的概率.如图 4所示，利用残差神经网络和长短时记忆网络预测相邻残基二面角.输入特征与距离预测网络相同，网络架构类似.通过最后一个残差块输出64×L×L为特征数据，输入到128个隐藏单元的双向递归LSTM层[44]，将特征数据的每一行嵌入到单个256向量中.由于每一行都嵌入在一个向量中，将特征数据转化为256×L二维张量，模型的输出层由1×1的fliters的二维卷积层和一个Softmax函数组成，根据相邻残基二面角φ、ψ、ω离散的24个角度区间，输出二面角在各个角度区间的概率.

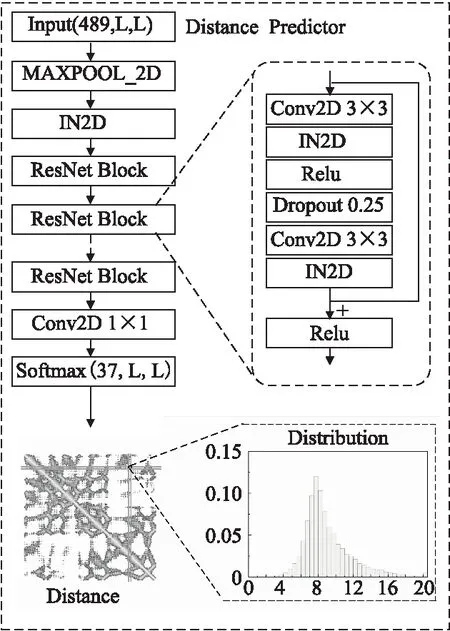
图2 残基间距离预测网络Fig.2 Distance prediction network between residues

图3 特征条带化过程Fig.3 Feature striping process

图4 相邻残基间二面角预测网络Fig.4 Dihedral angle prediction network between adjacent residues

2.5 训练过程

从数据集中随机选择6000个蛋白质作为训练集，711个蛋白质作为验证集.使用CrossEntropyLoss损失函数来衡量残基间距离预测网络和二面角预测网络的损失.通过迭代的方式来训练模型参数.训练过程包含整个数据集蛋白.每代训练完后，对训练集蛋白质顺序打乱，防止训练过程中形成记忆.在验证集上估计这代模型参数的效果，验证集中每个蛋白，针对欧式距离小于20Å残基对，将预测的距离概率分布去除第一个距离区间的概率(预测距离在2Å～20Å之外)，进行概率归一化，利用距离区间的中值和概率的乘积之和得到预测的残基间距离，计算残基间真实距离和预测的距离的绝对平均误差.如果绝对平均误差和损失loss在减小，保存这代训练的模型参数，总共执行100代.使用Adam优化算法[45]，计算高效，能较好的处理稀疏梯度，学习率为0.001，为了增加数值计算的稳定性，一阶矩阵的指数衰减率β1和二阶矩阵的指数衰减率β2分别设置为0.9和0.999，为了防止梯度计算过程中0被作为除数，模糊因子设置为1e-8，衰减权重设置为0.如果连续10代绝对平均误差和loss不降低，提前终止训练.在一块NVIDIA泰坦RTX GPU上训练好网络模型参数需要6天.

2.6 基于能量极小化的蛋白质建模

GCPFold采用能量极小化方法对蛋白质进行结构建模.将主干二面角的预测值设置为初始二面角，将预测距离分布转化为残基间势能.基于距离的势能与Rosetta能量函数共同作为约束指导蛋白质折叠.

距离分布转化为能量势能.首先将[19.5Å，20Å]距离区间设为参考状态，通过公式(11)将概率分布转化为势能分数.

(11)

其中Pi表示第i个距离区间的概率分布，k表示距离区间的数量，α表示基于距离标准化常量1.57[46].bini为第i个距离区间的中值.利用Rosetta中的SPLINE函数将公式(11)计算的分数转化成平滑的能量势，作为约束来指导蛋白质建模.为了加快建模速度，使用基于拟牛顿的能量极小化方法建立质心模型.基于LBFGS算法进行优化，结合Armijo一维线性搜索方法求取能量函数极值点[47].迭代进行1000次，收敛阈值设置为0.0001.GCPFold还使用了Rosetta能量项[48]：基于统计的rama二面角统计分布知识能量势能、空间排斥范德华力vdw、扭转偏好的Ramachandran、质心主链氢键cen_hb，Distance能量势和Rosetta能量项的权重分别设置为4、2、3、3、1.

由于Minmover算法易陷入局部最小值，对输入的初始结构和约束很敏感，GCPFold将预测的二面角加入扰动的方式引入随机效应策略，设置5个不同二面角的初始结构.以0.1为阈值，考虑在2Å～20Å内残基对的概率值，将概率高于此阈值的距离分数保留作为约束.对于每个初始结构，通过约束来建立模型.总共生成5个质心模型，利用Rosetta中的FastRelax进行全原子细化，选择能量最低的全原子模型作为最终模型.

3 结果分析

3.1 Contact精度比较

GCPFold预测蛋白质结构的关键是预测距离精度，为了保证建模精度，本文首先对预测的距离进行评估.不同的距离预测方法划分不同的距离区间.为了与其他方法进行公平比较，将GCPFold预测的距离分布归并成残基间接触和非接触的概率值.根据CASP准则，由中程(序列间隔在12～24之间)以及远程(序列间隔大于等于24)的前L/5、L/2、L精度的接触来评估接触预测的精度.本文将预测的距离分布小于8Å的概率累加得到残基对接触的概率.在80个测试集蛋白上评估预测残基间距离精度.

表1总结了GCPFold、RaportX[49]、DMP[50]3种方法在80个测试集蛋白上中程和长程接触预测的精度.结果表明在所有划分长度的范围内，GCPFold的接触预测精度最高.相比于RaportX接触预测方法，GCPFold预测的中程接触的前L/5、L/2和L的平均精度，分别比RaportX的精度提高了8.8%、11.4%和13.5%，预测的长程接触的前L/5、L/2和L的平均精度，分别比RaportX接触预测的精度提高了10.6%、11.2%和12.7%.相比于DMP接触预测方法，GCPFold在中程前L/5、L/2、L的平均精度，分别比DMP的精度提高了0.6%、0.7%和0.9%，预测的长程接触的前L/5、L/2、L的平均精度，分别比DMP的精度提高了1.1%、0.6%和1.2%.在测试集蛋白上GCPFold所构建的接触预测模型比其他方法精度更高.值得注意的是，这些方法都用了协同进化信息，可能由于神经网络训练过程中有效地整合了原始的协同进化信息，使得GCPFold预测的残基间接触精度更高，也可以推断出预测的距离分布有良好的精度.

3.2 不同特征组合对Distance预测精度的影响

与其他方法相比，GCPFold的一个重要方式利用了定义在单个残基上的特征序列谱、位置熵，定义在残基对上的特征互信息、去除背景噪声的互信息、接触势能、CCMpred计算的耦合分数、协方差矩阵，并设计深度学习网络架构用来预测残基间的距离信息.基于不同的特征组合对距离预测精度的影响做了验证.保持网络架构一致，基准实验1(Base1)利用协方差矩阵作为唯一输入来预测残基间距离，基准实验2(Base2)利用协方差矩阵、序列频率谱和CCMpred计算的耦合分数特征组合作为输入来预测残基间的距离，基准实验3(Base3)利用上述全部特征组合作为输入来预测残基间距离.如表 2所示，在80个测试集蛋白上，Base3预测的中程接触的前L/5、L/2和L的平均精度，分别比Base1的中程接触预测精度提高了3.1%、3.2%和5.5%，预测的长程接触的前L/5、L/2和L的平均精度，分别比Base1的长程接触预测精度提高了3.2%、5.7%和6.9%.Base3预测的中程接触的前L/5、L/2和L的平均精度分别比Base2的中程接触预测精度提高了1.0%、1.0%和1.0%，比Base2的长程接触预测精度提高了0.5%、0.7%和1.4%.由此可见，基于MSA提取的特征均对残基间距离预测有效.

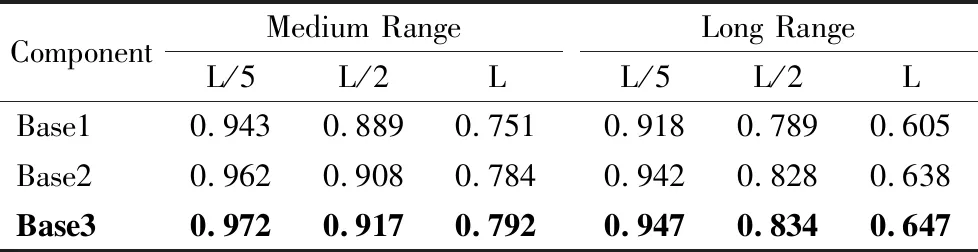
表2 不同特征组合在测试集上接触精度比较Table 2 Comparison of contact accuracy of different feature combinations on the test set

3.3 预测二面角的作用及方法整体性能

关于二面角预测网络，在80个测试集蛋白上，φ的平均绝对误差约为22.4°，ψ的平均绝对误差约为29.7°.由于ω角度比较稳定，不对预测的ω角分布做处理.GCPFold仅用预测的二面角来生成初始二面角.首先将预测的二面角分布利用每个角度区间的中间值和概率之积，累加得到相邻残基的φ、ψ，将φ、ψ随机添加[-15°，15°]内的随机角度，设置5个不同的φ、ψ的初始二面角，将ω全部设置为180°.利用Rosetta的SPLINE函数将公式(11)计算的分数转化成平滑的能量势.基于拟牛顿的能量极小化方法建立质心模型，使用LBFGS算法优化，利用Rosetta中的FastRelax进行全原子细化，选择能量最低的全原子模型作为最终模型.

本文验证了预测二面角的有效性.在约束条件下，通过预测二面角设置初始二面角和随机初始化二面角对蛋白质建模精度进行比较.采用TM-score[51]作为蛋白质结构拓扑相似性的评价指标，TM-score≥0.5表示预测的蛋白质与天然态蛋白质具有相似的拓扑结构.采用预测的二面角作为初始二面角，在80个测试集蛋白上的平均TM-score为0.725.相比于随机初始化二面角，其在80个测试集蛋白上的平均TM-score为0.659.采用预测的二面角在评价指标上均值比随机二面角高10.0%.具体到每个蛋白来说，采用预测的二面角作为初始二面角在约束条件下的建模结果在TM-score上有64个超过了采用随机二面角方式建模结果，占总数的80%，如图 5(a)所示，可直观反映预测二面角的作用.灰色实心圆代表TM-score指标的值，对角线上的点代表两种方法性能相同，颜色越深代表该位置蛋白质数量越多.TM-score对比图中的灰色圆总体分布于对角线下方，说明采用预测二面角作为初始二面角相比于随机二面角有助于蛋白质建模，但是依然存在部分蛋白质建模结果不佳.对于这些蛋白，考虑到预测的二面角误差较大，进而通过预测的二面角作为初始二面角在约束下结构建模精度低于随机二面角.GCPFold建模方法和RaportX建模方法做了比较，如图5(b)所示，在80个测试集蛋白上本方法建模精度平均TM-score为0.725，相比于RaportX，其在80个测试集蛋白上的平均TM-score为0.676，本方法在评价指标上均值比RaportX高7.2%.证明了GCPFold建模方法的先进性.如图 5(c)所示，GCPFold预测的蛋白质结构与天然态结构之间的比对图，其中包括β和α/β折叠类型，可以发现GCPFold预测的模型与天然态结构具有很好匹配度.

图5 (a)使用预测的二面角和随机二面角对蛋白质建模精度比较，(b)表示GCPFold与RaportX蛋白建模精度的比较，(c)表示GCPFold预测结构与天然结构的比对Fig.5 (a) Use predicted dihedral angles and random dihedral angles to compare the accuracy of protein modeling，(b) Represents the comparison of GCPFold and RaportX protein modeling accuracy，(c) Represents the comparison between the predicted structure of GCPFold and the natural structure

综上所述，GCPFold基于深度学习几何约束预测的建模方法，精确预测残基间距离和二面角，通过预测的二面角设置初始二面角，并基于距离分布建立约束进行蛋白质建模，有效提升了蛋白质建模的精度.

4 结 论

从蛋白质序列到三维结构的折叠算法一直是生物信息学的研究热点.针对蛋白质结构预测问题，本文提出了一种基于深度学习几何约束预测的蛋白质建模方法.从蛋白质序列出发，利用HHblits、Jackhmmer分别从Uniclust30、UniRef90序列数据库搜索蛋白质的MSA.从序列MSA中计算单位点氨基酸频率谱、位置熵，残基间互信息、去除背景噪声的互信息、协方差矩阵、接触势能，并利用CCMpred计算的耦合分数，将特征组合输入到神经网络中预测残基间距离分布和主干二面角分布.基于能量极小化的优化方法，由预测出的二面角信息加入扰动，引入随机效应策略，设置初始二面角，由预测的距离分布转化为能量势能，指导蛋白质折叠.与RaportX建模方法相比，在80个测试集蛋白上的实验结果表明，所提出的GCPFold方法具有先进性.

在下一步研究中，将探索新的深度学习网络架构以及新的蛋白质协同进化特征来预测残基间几何约束.考虑将预测的二面角转化为势能，设计能量函数指导蛋白质建模，并建立蛋白质残基级的模型质量评估，对预测的模型进行评估，形成闭环迭代的蛋白质结构预测.同时，在以后的研究中，将探索新的优化算法来进一步提高蛋白质结构预测精度，如多模态优化方法等.