面向路网的空间众包三维匹配任务点选址算法
2022-08-29孙玉娥
朱 菲,刘 安,孙玉娥,李 姝
1(苏州大学 计算机科学与技术学院,江苏 苏州 215006)
2(苏州大学 轨道交通学院,江苏 苏州 215137)
3(沈阳理工大学 装备工程学院,沈阳 110159)
E-mail:anliu@suda.edu.cn
1 引 言
随着移动互联网的发展和基于GPS的智能设备的普及,空间众包逐渐吸引了来自工业界和学术界的广泛关注.近年来,基于空间众包的应用快速发展,越来越多的人可以在众包平台发布带有空间属性的任务,平台指派合适的工人前往指定地点完成任务.如在滴滴打车中,用户向平台上传自己所在的具体位置,被分配到该订单的司机需要到达该位置接到乘客,载乘客移动到目的地后获得报酬.
在已有的关于空间众包的工作中,综述[1]对空间众包的研究现状与未来发展进行了总结,任务分配被认为是该领域的核心问题之一.以往解决任务分配问题的工作大都是对任务和工人两类对象进行匹配,根据任务属性从空闲工人池中挑选符合条件(如技能、可信度等)的工人,通知其前往用户指定的地点执行任务.在这一过程中,工人需要前往完成任务的地址由用户决定,平台并不参与.但这一假设并不总是成立,例如在美容美发类O2O应用南瓜车中,平台需要为工人和用户指定合适的任务场所.
受到这一启发,我们发现在很多空间众包场景中,任务地点可以很大程度上影响原有的任务-工人两类对象任务的效果.以空间众包中经典的打车场景为例,在图1中有一个用户u1和两个网约车司机w1、w2.如果任务点就设为用户所在的位置坐标,考虑到在路网下w1到u1的距离小于w2,传统匹配算法通知w1前往u1的位置接送乘客.然而,如果平台可以建议用户移动到附近的旗标处p1,那么w2到上车点的路网距离将大大减少.改变上车点后,平台会将该订单分配给路网距离更短的w2而非需要绕路的w1,用户也能更快坐上车开始行程.
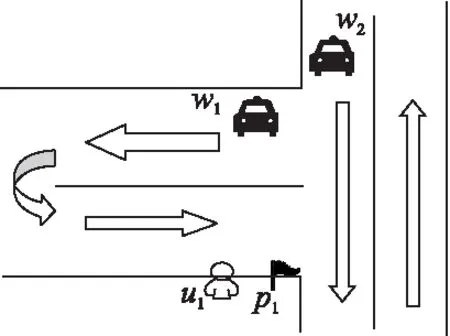
图1 打车场景中的任务点选址示例图Fig.1 Example of task location in taxi scenario
基于这种发现,我们首次提出了面向路网的空间众包三维匹配任务选址问题.通过在用户允许范围内调整任务地点,能最大化地节约工人们的旅行成本,在宏观角度上减少碳排放.同时,为了避免因刻意追求减少旅行成本而选择距离较远的不合适的工人,我们不仅选择任务点,还挑选合适的工人,保证在工人旅行成本减小的同时,工人到任务点的距离也尽可能减小,从而减少用户的等待时间.显然,该工作可以应用在许多空间众包场景(如外卖配送),这也证实了我们所提出的问题具有广泛的现实意义.同时需要说明的是,目前没有相关工作与本文问题的优化目标一致,且涉及到工作地点的分配工作都是基于欧式距离展开研究,所以现有算法不能直接解决本文问题.
为了解决本文所提出的任务点选址问题,我们首先将原问题规约到最大三维匹配问题,证明其在多项式时间内不能被找到最优解.由于在将原问题建模到三分图结构的过程中,我们需要对路网空间中的所有用户、工人和任务点两两进行检查,确认是否满足给定约束.由于待验证的对象数量往往很庞大且实际满足限制的对象是少量的,所以遍历浪费算力和时间.并且,对于每一个用户-任务点-工人组合,我们都要计算工人节约的旅行成本和最终移动距离,每一次计算都包括多次路网下的最短路径查询.显然,如果使用朴素解法,这一过程的用时在现实场景中是不可接受的.因此我们提出了筛选可用匹配对的优化算法,通过空间索引快速查找指定范围内的对象,并优化多点对间的最短路径查询,对大量重复计算的最短路径进行提取复用.然后,本文对任务点容量充足/不足的情况进行分析,并证明了前者可用二分图完美匹配的Kuhn and Munkres算法(下文简称KM)解决,针对后者提出了分块贪心算法.本文的具体工作如下:
1)首次提出了空间众包中的路网环境下的三维匹配任务点选址问题.该问题通过调整任务点并根据调整后的任务点选择工人,旨在最大化节约的工人的旅行成本并使用户的等待时间尽可能小.
2)通过对该问题进行规约,我们证明其具有NP难度.本文首先提出了筛选可用匹配对和多点对最短路径查询优化算法,并在此基础上将原问题的不同情况分别建模到二分图和三分图上,最终给出贪心解法.
3)为了评估本文算法的性能,本文在真实数据集上进行了实验,证明了所提出算法在效用和时空开销方面都有很好的表现.
本文的其余内容组织如下:第2部分讨论与本文相关的已有工作;第3部分介绍问题定义并证明其复杂度;第4部分提出解决方案;第5部分给出实验结果并进行分析;第6部分总结全文.
2 相关工作
本章首先介绍了空间众包中任务分配领域的经典工作,然后特别讨论了3类对象匹配中与本文相关的工作,并进行了区分.
2.1 任务分配
综述[1]将现有的空间众包研究归纳为4个方向:任务分配、质量控制、激励机制和隐私保护,其中任务分配一般被划分为匹配问题和调度问题.
作为被公认为空间众包领域的核心问题,大部分任务分配都是对任务和工人2类对象进行匹配,旨在在满足平台和用户约束的前提下实现不同的优化目标.文献[2]考虑任务数相对于工人数非常稀缺的情况并提出了一种公平的分配方式.考虑到不同类型的任务,如多人合作和有技能需求,学术界也涌现了一批优秀工作.文献[3]针对需要多人合作的任务提出了能够最大化合作效用的分配方式.文献[4]提出了多技能导向的任务分配问题,并给出了多种有效算法.同时,由于空间众包的任务分配过程中通常涉及到一些敏感信息,如坐标位置和任务报价等,隐私保护技术也被应用在大量的任务分配工作中.文献[5]实现了在满足社会利益最大化的同时保护隐私的任务分配.
与上述两类对象匹配不同,本文考虑任务点对于分配效果的影响.由于现实中存在很多需要平台确定任务地址的场景,所以我们的想法更加全面与新颖.
2.2 3类对象匹配
近年来,有少数任务匹配工作也将任务点作为需要匹配的第3类对象.从匹配问题的优化目标上看,工作[6]最大化完成的任务-工人匹配对的效用,而文献[7]最大化稳定匹配数.文献[8]中,平台为每个骑手规划路线,包括购买某件物品的具体位置,使得物品质量、工人评分和奖赏综合效用最高.但是他们并不考虑任务地点改变对工人旅行成本产生的影响,而本文以此任务点选址的首要目标,因此这些工作并不完全适用于我们的问题.并且相比工作[6]直接将容量为n的对象拆分成n个容量为1的对象建模并统一进行三维匹配,我们分情况讨论并规约到二分图匹配和三维匹配问题,能适应更多场景.
3 问题定义和复杂度
本章先给出形式化的问题定义,然后给出本文问题的复杂性分析.
3.1 问题定义
首先介绍4个基本概念,然后给出可用三维匹配的定义及其效用的计算方式,最后定义路网环境下的空间众包三维匹配任务点选址问题.
定义1.(路网)路网定义为一张有向带权图G=
定义2.(用户)一个用户定义为u=
定义3.(工人)一个工人定义为w=
定义4.(任务点)一个任务点定义为p=
定义5.(可用三维匹配)一个用户-任务点-工人三维匹配(u,p,w)可用,当且仅当它满足下列约束:
1)任务点p在用户u愿意接受的移动范围内,即d(lu,lp)≤ru;
2)任务点p在工人w愿意接受订单的地理范围内,即d(lw,lp)≤rw;
3)相比工人w需要移动到用户所在位置lu的路网距离d(lw,lu),他/她到任务点p的路网旅行成本d(lw,lp)更短,即dt(u,p,w)=d(lw,lu)-d(lw,lp)>0.

定义6.(面向路网的空间众包三维匹配任务选址问题)给定路网G中的用户集合U={u1,…,um},工人集合W={w1,…,wn}和任务点集合P={p1,…,pk},本问题的求解目标是找到U,W,P的一个可用三维匹配集合M⊆U×P×W使得该集合的总效用最大化,即Maximizeμ(M)=∑(u,p,w)∈Mμ(u,p,w),且满足以下约束:
1)可用性约束:集合M中的每个三维匹配都是可用的,即都满足定义5中的所有约束.
2)唯一性约束:每个用户u在M中至多出现一次,每个工人w在M中至多出现一次;
3)容量约束:每个任务点p在M中至多出现cp次.
3.2 问题复杂性
定理1.面向路网的空间众包三维匹配任务点选址问题具有NP难度.
证明:考虑原问题的一种特殊情况:在欧式空间中,提交了订单的用户数、工人数和任务地点数相等,每个任务点的容量都为1,每个可用三维匹配对中工人节约的旅行距离和最终移动距离相等.此时,该问题等价于三维匹配问题的优化问题,而三维匹配问题的决策问题已经被证明是NP完全问题[6].
另外,本文问题的难度远超上述的特例,无论是路网中的距离计算更为复杂,还是需要考虑到容量等其他约束.因此,面向路网的空间众包三维匹配任务点选址问题也至少是NP难度的.
4 解决方案
本章首先给出解决本文面向路网的空间众包三维匹配任务点选址算法(下文简称路网下的任务点选址算法)框架;随后依次介绍框架中基于筛选可用匹配对和多点对间最短路径距离的优化算法;最后,对上车点容量不同的情况进行分析,证明了上车点充足时的原问题可用二分图中的KM算法[9]解决,并给出了解决上车点不足场景下的原问题的分块贪心算法.
4.1 路网下的任务点选址算法框架
在本文问题中,在给定路网环境下,平台掌握着在原地等待服务的m个用户,n个空闲工人和k个适合作为任务场所(如司机等待乘客)的任务点的相关信息.目标是为每个订单请求指定一个任务点和分配一个工人,使其能与发起订单的用户构成一个可用三维匹配对,最终能最大化平台上所有可用三维匹配对的效用之和.值得注意的是如定义5中所示,每个可用三维匹配对的效用越大,说明该订单所指派工人能节约的旅行成本越大,同时他/她最终移动到任务点的旅行成本越小,即用户等待工人的越短,这显然是考虑到工人和用户双方利益的.
为解决该问题,一种最直观的思想是遍历所有的用户-任务点-工人,一一检查是否能满足限制.找到所有的可用三维匹配对后,逐一计算它们的效用值.之后尝试组合已有的可用三维匹配对,构造出所有满足定义6中约束的集合,最终比较得出最优解M.然而在现实应用中,在筛选可用匹配对时,需要计算用户-任务点和工人-任务点之间的距离判断是否满足空间约束.显然这一过程是极其耗时的,因此我们加入了筛选可用匹配对优化算法(算法2),通过建立空间索引进行加速.同时在计算每个可用匹配对的效用时,需要计算其中的工人-任务点和工人-用户的最短路径距离.同样地,我们基于精度换速度的思想,提出了多点对间的最短路径长度计算优化算法(算法3),大大加快了点对之间的距离计算.最后,由于对可观数量的可用三维匹配对进行组合后暴力查找最优解的解空间是很庞大的,所以我们对上车点容量充足和不足的情况做了分析,对于前者我们使用KM算法(算法4)进行求解,对于后者我们在已有的三维匹配贪心算法上进行了分块优化并求解(算法5).
算法1.路网下的任务点选址算法框架
输入:道路网络图G,用户集U,工人集W,任务点集P
输出:可用三维匹配集合M
1.筛选可用三维匹配对(U,P,W)//算法2
2.Foreach可用三维匹配对(u,p,w)
3. 计算μ(u,p,w)//算法3
4.Ifmax(cp)≥|U|
5. KM算法求得最优匹配M//算法4
6.Else
7. 分块贪心算法求得最优匹配M//算法5
8.根据匹配M通知相应的工人和用户前往任务点
本文所提出的路网下任务点选址算法框架的伪代码如算法1所示.
4.2 筛选可用三维匹配对优化算法
如引言部分所述,平台上提交订单的用户数,等待分配的工人数和有剩余容量的任务点数都是非常庞大的,然而它们能组成的可用三维匹配对数却是较小的.鉴于此,首先分析朴素遍历找到可用匹配对方法的复杂度,之后提出一种优化算法,利用Rtree结构快速筛选可用的三维匹配对.
首先介绍朴素遍历寻找可用三维匹配对的方法,并分析其复杂度.如图2所示,平台上有用户集合U={u1,…,um},工人集合W={w1,…,wn}和任务点集合P={p1,…,pk}.对每个用户ui,要对p∈{p1,…,pk}逐一进行检查:如果d(lui,lp)≥rui,则该用户愿意前往该任务点(图2中用实线表示);否则,用户ui不能和任务p在同一个可用三维匹配对中(图2中用虚线表示).遍历得到ui愿意前往的所有任务点集合P(ui)后,对其中的每个任务点p,继续对每个空闲工人w∈{w1,…,wn}进行遍历:如果d(lw,lp)≥rw,则该工人愿意移动到该任务点工作(图2中用实线表示);否则,工人w不能和任务点p在同一个可用三维匹配对中(图2中用虚线表示).如此,经过先后对任务点集合和工人集合的遍历,我们找到了所有包含用户ui的可用三维匹配对.因此,用朴素遍历算法找到本文问题中所有用户的可用匹配对的时间复杂度为O(m×k×n),这在现实场景中显然是不可接受的.
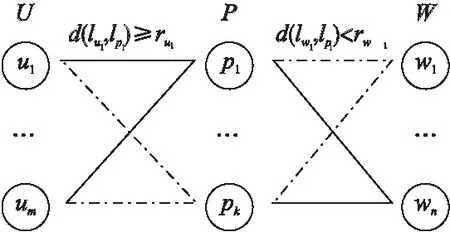
图2 三维匹配问题示例图Fig.2 Example of 3-dimensional matching
本文利用Rtree中能快速搜索指定空间范围内的点的特性,提出一种筛选可用匹配对优化算法.基本思想是根据所有任务点的位置建立一棵Rtree,再对每个工人搜索其工作范围内的任务点,并为任务点添加愿意前往该地址的工人标签.然后对每个用户在Rtree中快速搜索他/她活动范围内的任务点,并根据这些任务点的工人标签直接构建该用户的可用三维匹配对.
伪代码如算法2所示.输入为路网G下的用户集合U、工人集合W和任务点集合P,输出为所有可用三维匹配对组成的集合M′.在执行过程中,首先为所有任务点所在的区域建立RTree空间索引(第1行),然后对每个任务点p,初始化愿意移动到lp完成任务的工人标签为空集(第2-第3行).随后,对每个工人w在Rtree中搜索他/她愿意活动的区域内的所有任务点P(w),并在这些任务点的工人标签中添加w(第4-第7行).接下来,对提交任务请求的每个用户u,在Rtree中搜索他/她愿意前往的所有任务点P(u)(第8-第10行),并检索每个可达任务点p∈P(u)的工人标签p.workers,然后依次将标签内的工人w∈p.workers、任务点p和用户u组成可用三维匹配对(u,p,w)(第11-第13行).
算法2.筛选可用三维匹配对优化算法
输入:道路网络图G,用户集U,工人集W,任务点集P
输出:可用三维匹配对集合M′
1.根据P中的任务点经纬度坐标lp建立Rtree
2.Foreachp∈P
3.p.workers=φ
4.Foreachw∈W
5.areaw为以lw为圆心rw为半径的圆外切正方形区域
6. 在Rtree中搜索与areaw重叠区域内的任务点P(w)
7.p.workers.add(w)
8.Foreachu∈U
9.areau为以lu为圆心ru为半径的圆外切正方形区域
10.在Rtree中搜索与areau重叠区域内的任务点P(u)
11.Foreachp∈P(u)
12. Foreachw∈p.workers
13.M′.add((u,p,w))
14.返回M′
4.3 最短路径长度计算优化算法
得到集合U×P×W中包含所有可用三维匹配对的集合M′后,需要计算其中每个可用三维匹配对(u,p,w)的效用μ(u,p,w),其中涉及到工人-任务点和工人-用户之间的最短路径长度计算.考虑到现有的一些最短路径算法不能很好地平衡精度与速度,如Dijkstra算法[10]复杂度较高,A*过于依赖潜在价值函数的设计,本文借鉴了文献[11]中避免很多相邻的点对之共用的部分最短路径被多次重复计算的基本思想,提出了基于路网的任务点选址场景下的最短路径长度计算优化算法.
下面以图3为例解释在面向路网的任务点选址场景下的最短路径长度计算优化算法.首先将可用三维匹配对中出现的所有用户{u1,u2}、任务点{p1,p2}和工人{w1,w2,w3}根据他们经纬度坐标映射到路网平面中的一批位置点.其次对所有用户点进行聚类并找到该用户簇的中心位置点lCU,并依次类推对任务点和工人聚类后找到中心点lCP和lCW.之后计算并保存两个簇中心点间的最短路径长度,作为簇之间的距离.此时,如果要计算两类对象点(用户-工人,或用户-任务点)之间的最短路径长度,就可以转化为求两个位置点分别到所在簇的中心点的距离与两个簇之间距离的和.如果要计算可用三维匹配对(u2,p1,w3)的效用,按照定义5有μ(u2,p1,w3)=d(lw3,lu2)-d(lw3,lp1)/d(lw3,lp1),那么在该最短路径长度计算优化算法中d(lw3,lu2)=d(lw3,lCW)+d(lCW,lCU)+d(lCU,lu2).同样地,d(lw3,lp1)=d(lw3,lCW)+d(lCW,lCP)+d(lCP,lp1).显然在簇之间的最短路径被提前计算并保存下来时,相同的两个簇内的多点对间最短路径长度可以避免大量重复计算.因为本文中对于所有可用三维匹配对都涉及两次最短路径长度计算,所以这一优化可以大幅降低计算耗时,提高本文解决方案的效率.
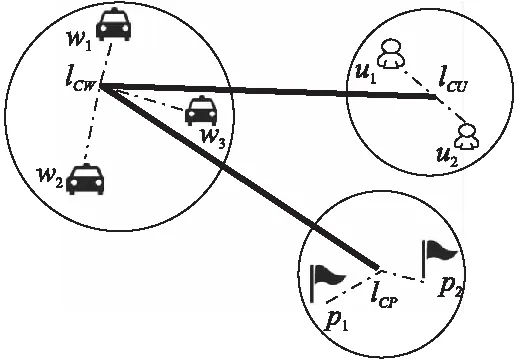
图3 最短路径长度计算优化算法示例图Fig.3 Example of optimization algorithm for shortest path length calculation
算法3.最短路径长度计算优化算法
输入:路图G,用户集U,工人集W,任务点集P,起点s∈W,终点t∈U∪P
输出:起点s到终点t的最短路径长度d(ls,lt)
1.根据U中的用户经纬度坐标lU层次聚类成簇集CU
2.numu=len(CU)
3.Foriin[0,numu-1]
4. 确定CU[i]的中心点位置lCU[i]
5.根据P中的工人经纬度坐标lP层次聚类成簇集CP
6.nump=len(CP)
7.Forjin[0,nump-1]
8. 确定CP[j]的中心点位置lCP[j]
9.根据W中的任务点经纬度坐标lw层次聚类成簇集CW
10.Foreachcluster∈CW
11. 确定cluster的中心点位置lcluster
12. Foriin[0,numu-1]
13. 计算并保存两个簇中心间的距离d(lcluster,lCU[i])
14. Forjin[0,nump-1]
15. 计算并保存两个簇中心间的距离d(lcluster,lCW[j])
16. 找到s所在的工人簇Cs
17. 计算s到簇Cs中心的距离d(ls,lCs.
18. 找到t所在的用户或任务点簇Ct
19. 计算簇Ct中心到t的距离d(lCt,lt)
20.d(ls,lt)=d(ls,lCs)+d(lCs,lCt)+d(lCt,lt)
最短路径长度计算优化的伪代码如算法3所示.输入为路网G下的用户集合U、工人集合W、任务点集合P、一个起点s(对象类别为工人)和一个终点t(对象类别为用户/任务点),输出为起点到终点的最短路径长度d(ls,lt).值得注意的是,第1-第15行为对给定工人、用户和任务点的数据预处理部分,仅第16-第20行是给定起点和终点后计算最短路径长度所需的操作.在执行过程中,首先为所有用户进行层次聚类,停止条件为两个用户簇之间的距离超过指定阈值,并找到每个用户簇中所有位置点坐标的平均值坐标点作为该簇的中心点位置(第1-第4行).并对路网中的所有任务点做同样的操作(第5-第8行).接着,在对所有工人进行聚类并确定中心点(第9-第11行)后,提前计算并保存工人簇到其他两类对象簇的最短路径距离(第12-第15行).给定一个起点s后,首先找到它所在的簇,并计算s到该簇中心点lCs的路网距离(第16-第17行).随后,找到给定终点t的所在簇和簇中心点lCt到t的最短路径长度(第18-第19行).最后,查找数据预处理阶段保存的起点所在簇到终点所在簇之间的距离d(lCs,lCt),并加上两个端点与其所在簇中心点的距离,就是所求的起点s到终点t的最短路径长度(第20行).
4.4 任务点容量充足时的任务选址算法
通过上述两个优化算法,得到原路网下的任务点选址问题中的所有可用三维匹配对的集合M′和其中每个可用三维匹配对的效用.本部分首先证明在所有任务点的容量超过用户数量时,原问题可以规约到二分图的完美匹配问题,然后给出基于KM算法的解决办法.
定理2.给定所有可用三维匹配对的集合M′,其中有用户集合U={u1,…,um},工人集合W={w1,…,wn}和任务点集合P={p1,…,pk},如果min{cp1,…,cpk}≥m,原问题可以规约到二分图上的完美匹配问题.
证明:给定用户ui和工人wj,称能与他们组成可用三维匹配对且效用最高的任务点为p.由于每个任务点的容量都大于等于用户数,所以即使其他所有的用户-工人组合都在任务点p处取得最高效用,用户ui和工人wj仍然能在p处执行任务,即取到最高效用μ(ui,p,wj).则原问题的目标是找到一个集合M⊆M′,所有用户在其中至多出现一次,且M中所有可用三维匹配对的效用之和最高.
构造一个二分图,两个互不相交的点集合为U和W,连接ui和wj之间的边权重为μ(ui,p,wj),其中p为能与ui和wj组成可用三维匹配对且效用最高的任务点.此时,原问题的目标可以规约到在构造的二分图中找到完美匹配M,本文使用经典KM算法[9]解决.
算法4.任务点容量充足时的任务选址算法
输入:道路网络图G,可用三维匹配对集合M′=U×P×W
输出:最优可用三维匹配对集合M⊆M′
1.Foreachu∈U
2.Mu为包含u的所有可用三维匹配对集合
3.Wu是Mu中的工人集合
4. Foreachw∈Wu
5.μu,w是Mu中包含u,w的三维匹配对的最大效用
6.构造二分图GM=(U,W)
7.二分图中边e(u,w)=μu,w
8.KM算法找到GM中的完美匹配M
9.返回M
任务点容量充足时的任务点选址伪代码如算法4所示.输入为路网G下的可用三维匹配集合M′=U×P×W,输出原问题所求的最优可用三维匹配对结合M.在执行过程中,首先对M′的每个用户u,找到能与其组成可用三维匹配对的工人集合Wu(第1~第3行).然后遍历该集合中的工人,计算包含u的可用三维匹配对的最大效用μu,w(第4-第5行).接着构造二分图GM,包括两个互不相交的结点集合U和W,连接两个结点u和w的边权重为μu,w(第6-第7行).最后,用经典KM算法找到GM中的完美匹配M,并作为路网下任务点选址问题在任务点容量充足时的最终解返回.
4.5 任务点容量不足时的分块贪心任务选址算法
当任务点容量不足时,可以将原问题规约到最大三维匹配问题,目标是在三分图U×P×W中寻找最大匹配M.由于在文献[12]中,最大三维匹配问题已经被证明是NP难的,所以无法在多项式时间内找到本文问题在任务点容量不足情况下的最优解.经典的近似算法有贪心和局部搜索,前者在每一次选择一条权值最大的边,后者每次替换已有匹配中的一条边来获得更好的匹配效果.然而,在空间众包场景中,3类对象(用户、任务点和工人)的数量非常庞大,所以以上两种近似算法的用时依旧不可小觑.同时,平台需要很快做出决策并通知相关工人前往指定任务点,否则用户和工人就会陷入空等.基于这种需求,本文对传统最大三维匹配问题中的贪心算法进行了优化,提出了分块贪心算法.
传统的最大三维匹配问题贪心算法在每一轮要遍历所有的边,找到一条权值最大的边e(u,p,w).在此之后,因为任务点p的剩余容量发生了变化,还要遍历所有剩余边去更新与p有关的边的权值.所以我们对原三分图进行了分块处理,按照路网中所有对象的位置聚类结果将其分成多个互不相交的三分图.经过这种处理,既能比随机拆分尽量少地降低精度,又能加快寻找最大边的过程,更能方便并行处理.下文以图4为例解释分块贪心任务点选址算法.
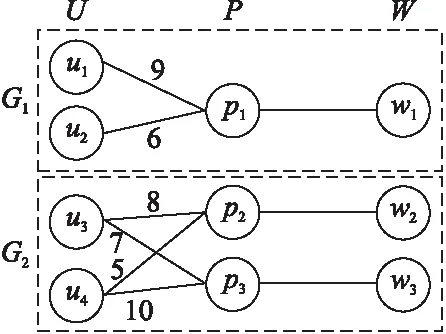
图4 分块贪心示例图Fig.4 Example of partitioned-greedy
对于平台上的所有3类对象(包括用户、任务点和工人)的位置点,统一按照经纬度坐标进行聚类.之后,根据聚类结果为每个簇建立三分图.如图4中就有为簇C1和C2和分别建立的三分图G1和G2,每个图包括对应的簇内所有位置点,每条连接3个点的边表示该簇内的可用三维匹配对.对每个三分图记录其中的最大边并记录其权值,如max1=9,max2=10.贪心地选择最大边(u4,p3,w3)后,仅需要更新三分图G2中与p3相关的边,之后重新计算该图中的最大边.在下一轮中,直接将更新后的max2=8直接与上一轮的max1比较,就可得到全局最大边.
任务点容量不足时的分块贪心任务点选址的伪代码如算法5所示.输入为路网G下的用户集合U、工人集合W和任务点集合P,输出为原问题所求的最优可用三维匹配对结合M.首先对路网中的所有对象点统一按照经纬度坐标进行聚类,得到簇集合C(第1行).之后在算法1和算法2的优化基础上,为每个簇建立三分图并计算每条边的权值,同时该簇的最大边及其权值(第2-第6行).由于每个用户在最终匹配中至多出现一次,所以在工人和任务点充足时共贪心选择m次最大边,对应m个用户提出的所有订单.在每一轮,将最大边p加入最终匹配集合后,更新该簇中与p共用任务点的其他边,并在剩余边中确定该簇的当前最大边继续与其他簇的最大边进行比较(第7-第11行).重复以上更新过程,直至最优可用三维匹配对集合M包含每个用户所在的边.
算法5.任务点容量不足时的分块贪心任务点选址算法
输入:道路网络图G,用户集U,工人集W,任务点集P
输出:最优可用三维匹配对集合M
1.对所有对象点进行聚类得到簇集合C={c1,…,cq}
2.Foriin[0,q-1]
3. 利用算法1找到ci中的可用匹配对组合Mi
4. 利用算法2计算Mi中每个匹配对的效用μ(Mi)
5. 根据Mi和μ(Mi)建立三分图Gi
6. 记录最大边权值maxi
7.Forjin[0,m-1]
8.p是权值为{max1,…,maxp}中最大值的边
9. 将边p加入最大匹配M
10. 更新p所在三分图中包含p的其他边
11. 更新该簇的最大边并记录权值
12.返回M
5 实验分析
5.1 实验数据集与参数设置
本文使用真实数据来测试所提出的方法.考虑到工人最大可接受范围rw和用户最大可接受范围ru的限制,工人和用户不会移动太远的距离,因此把所有对象都限制在一个城市内.本文选择西安作为目标城市,从滴滴打车1获取从2018年10月1日~2018年10月30日该市4500000条打车订单数据,包括订单编号和订单轨迹数据.订单轨迹点的采集间隔是2-4s,且已经做过绑路处理,保证数据都能够对应到实际的道路信息.若一个订单在短时间内出现两个轨迹点行驶方向相反,认为这个订单存在绕路接用户(乘客)的情况,我们抽取这种订单的初始轨迹点作为工人(司机)初始位置,绕路后的第一个轨迹点作为用户初始位置.之后从OSM(OpenStreetMap:一个开源的地图数据社区)获取西安路网数据,并导出路网数据中的节点作为获取候选上车点.最终,本文中所使用的数据集包含50000个工人,10000个用户以及100000个候选任务点.
表1展示了本文实验的参数设置,其中黑体字表示实验的默认参数.在每一个实验中,只改变其中一个参数,展示被测方法的效用和运行时间,其余参数保持默认值.

表1 实验参数Table 1 Experimental parameters
5.2 对比算法
如前文所述,在任务点容量充足的情况下,我们将原问题转化成二分最大匹配问题;在任务点容量不足的情况下,转化为最大三维匹配问题.对于前者,可用KM算法求得最优解;对于后者,可用贪心算法求得较优解.为了证明本文所提出的筛选可用三维匹配对优化算法和最短路径长度计算优化算法的优化效果,本文会在KM和贪心两种传统算法的基础上分别添加两种优化.具体来说:
1)对于KM算法不做任何优化,KM(o1)代表只使用筛选可用三维匹配对优化算法进行优化,KM(o2)代表只使用最短路径长度计算优化算法进行优化,KM(o1+o2)代表同时使用两种优化.
2)对于贪心算法不做任何优化,贪心(o1)代表只使用筛选可用三维匹配对优化算法进行优化,贪心(o2)代表只使用最短路径长度计算优化算法进行优化,贪心(o1+o2)代表同时使用两种优化.
在任务点容量不足的场景下,对于已经加入两种优化的贪心算法的基础上,本文又提出了贪心分块算法,能在略微降低效用的前提下明显减少运行用时.所以在将该算法与没有分块策略的贪心算法进行对比的同时,和其他两种三维匹配算法进行对比:
1)优化贪心算法:在解决最大三维匹配问题的贪心算法基础上采用筛选可用三维匹配对优化算法和最短路径长度计算优化算法.
2)局部搜索算法[6]:首先随机产生一个临时匹配集,之后不断对其中的每一个匹配,尝试能否更换为一个新匹配,使得不与其他匹配冲突的同时效用大于原匹配.
3)自适应阈值算法[6]:根据平台已有的三类对象确定初始阈值,在匹配过程中仅保留效用大于该阈值的三维匹配,并不断更新阈值.
5.3 实验结果和分析
本节首先进行实验,来证明本文所提出的两个优化算法的实际优化效果.随后在优化的基础上,将本文的贪心分块算法与其他三维匹配领域算法进行比较,并分析不同用户数量,不同工人数量,不同上车点数量对效用和计算时间的影响.
5.3.1 优化方法对实验结果的影响
从表2可以看出,在默认参数下,当任务点容量充足时,两种优化算法分别降低的效用较为微小,降低的运行时间较为明显.从表3可以明显看出,两种优化算法在任务点容量不足时也能大大提高传统贪心算法的效率.总体来看,本文所提的优化算法能以非常小的精度牺牲换取可观的效率提升,在两种不同情况下的实验也证实了其稳定性.

表2 两种优化方式在任务点容量充足时的效果Table 2 Effect of two optimization methods when the capacity of task locations are sufficient

表3 两种优化方式在任务点容量不足时的效果Table 3 Effect of two optimization methods when the capacity of task locations are insufficient
5.3.2 分块贪心算法的实验分析及参数影响
1)分块贪心算法的性能分析
从表4可以看出,无论所有参数如何变化,分块贪心算法的效用都维持在一个不错的水平.算法的效用与优化贪心算法几乎相同,稍低的原因是在分块的过程中仅考虑每个簇内的可用三维匹配对,而无视不同簇之间可能存在的高效用匹配对.而在局部搜索算法中,更多次的迭代决定了它能比局部最优的贪心算法找到更优解.但与此同时,分块贪心的效用也明显高于自适应阈值算法.
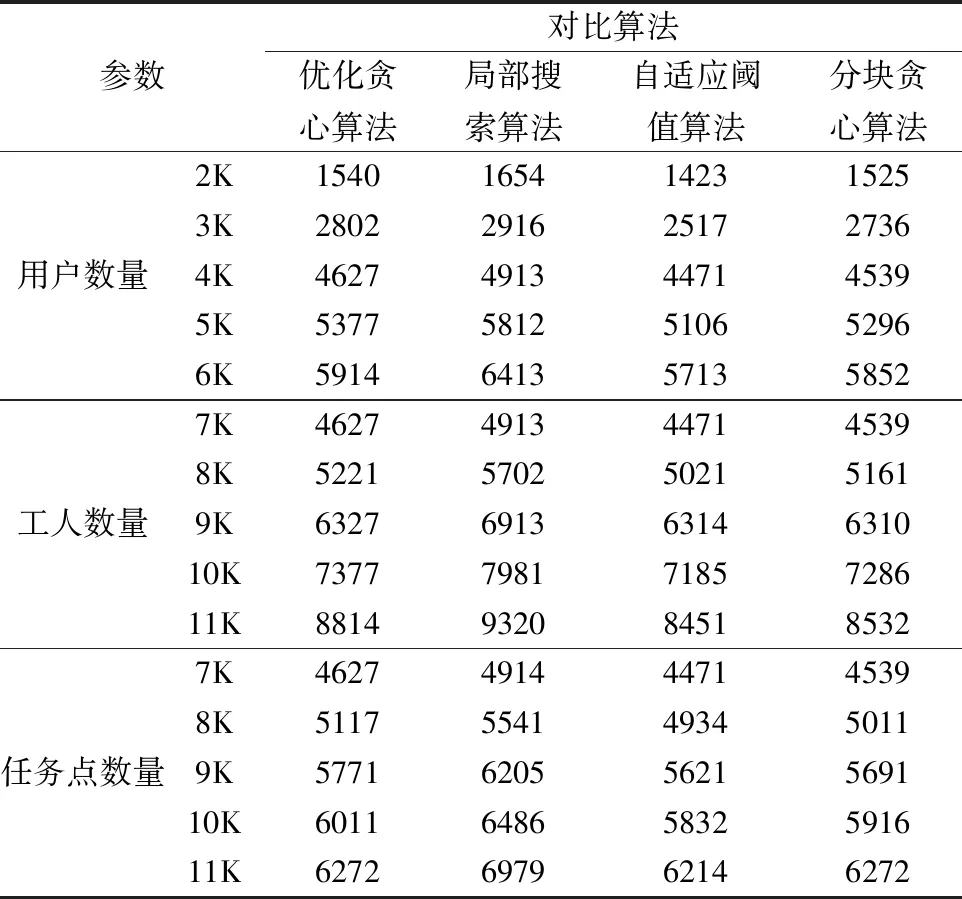
表4 不同方法在参数变化下的效用Table 4 Utilities of different methods under parameter changes
从表5可以看出,分块贪心算法的运行时间始终是所有对比方法中最低的,与优化贪心算法的时间差也有力证明了分块策略能明显提高计算效率.自适应阈值算法的用时表现不错是因为对于一些效用值低的可用三维匹配会被直接舍弃,所以在之后需要考虑冲突的三维匹配数量会大大减少.

表5 不同方法在参数变化下的运行时间Table 5 Running time of different methods under parameter changes
2)用户数量对实验结果的影响
从表4和表5看,随着用户数量的上升,所有算法的效用和用时都出现提升,这是因为可供选择的可用三维匹配增多.其中,分块贪心算法的效用略低于局部搜索和优化贪心算法,但分块贪心任务选址算法与传统贪心相比,运行时间有着显著的降低.
3)工人数量对实验结果的影响
从表4和表5也能看出不同工人数量对所有方法的效用和运行时间的影响.随工人数量增加,分块贪心算法与其他算法的表现差距稳定.相比优化贪心算法,分块贪心算法在效用只有微弱降低的情况下,运行时间都能实现明显减少.
4)任务点数量对实验结果的影响
如表4和表5所示,在任务点数量变化的前提下,分块贪心算法始终可以使用最少的计算时间并得到近似优化贪心的效用结果.再次证明了无论各类对象数量变化,本文所提方法表现稳定.
6 总 结
本文针对现有的空间众包任务分配工作忽视任务点位置对分配效果的影响和底层路网结构的不足,提出了面向路网的空间众包三维匹配任务点选址问题.本文根据任务点容量不同的场景分别进行分析:证明了容量充足时可以将原问题规约到二分图最大匹配问题,并且用经典KM算法获得最优解;对任务点容量不足情况下的原问题,本文提出了分块贪心算法.此外,本文还提出了两种优化方法,分别用于快速筛选可用三维匹配对和计算多点对之间的最短路径长度.最后,通过实验证明了本文所提解决方法能够兼具速度与精度.
