兼顾用户话语权的改进加权Slope-One协同过滤推荐

陈梅梅，董晨光，王 淇，戴伟辉

1(东华大学 旭日工商管理学院，上海200051)

2(复旦大学 管理学院，上海200433)

E-mail：cmm@dhu.edu.cn

1 引 言

电子商务的深入发展要求企业尽可能满足不同用户的兴趣爱好，个性化推荐技术应运而生.基于内存的协同过滤算法由于其推荐准确、效率高等特点在电商、影视、图书、音乐等平台得到广泛应用，但是，数据稀疏性一直是该类算法面临的一大瓶颈问题[1].用户-项目评分矩阵是协同过滤推荐算法的重要输入，源于用户的浏览、交易行为或评价结果.但在众多的项目中，每个用户都存在着大量未评分项目，因而，数据稀疏问题不可避免，且给协同过滤推荐算法中用户/项目相似性的精确计算带来了很大困难，并最终影响推荐准确度的提升.因此，对比协同过滤算法中数据稀疏性导致推荐精度问题的现有解决方案，选择简单有效的方案并针对其存在的不足加以改进，具有重要的理论和现实意义.

2 研究综述

为了降低数据稀疏性对协同过滤推荐的影响，现有研究中的主流方案一般有4类.

2.1 用户/项目聚类

先对用户或者项目进行聚类，再在几个具有相似性关系的组内分别对用户进行推荐[2]，通过缩小近邻用户的范围，在确保个性化同时最大限度地降低数据稀疏性影响，但用户或项目的聚类会导致一些有用个性化信息丢失.

2.2 改进用户/项目相似度计算方法

利用用户/项目的特征信息，基于用户/项目属性以及用户/项目之间的相似关系计算用户[3-5]或项目[6]特征相似度，通过避开对用户-项目评分矩阵的依赖，在一定程度上缓解数据稀疏性对推荐的影响，但融入基于社交网络等的用户/项目特征信息一定程度上会增加算法复杂度以及数据采集、清理和存储的要求.

2.3 基于矩阵分解技术的评分矩阵降维

主要采用奇异值分解法SVD(Singular Value Decomposition)[7，8]，通过将高维度的评分矩阵映射到低维度，能有效降低矩阵规模和数据稀疏性，但在矩阵运算的过程中将一个矩阵分解为多个矩阵的乘积，难免会丢失用户相似性信息.为此，林建辉等提出了一种基于SVD和模糊聚类的协同过滤算法，降维同时缩小近邻范围，缓解数据稀疏性同时提升可拓展性[9];刘晴晴等提出基于SVD的混合协同过滤推荐算法，先用SVD方法分解用户-项目评分矩阵，通过随机梯度下降法填充稀疏矩阵，并优化相似度计算方法以有效提高推荐准确性[10];Nilashi等则提出了基于SVD和本体论的混合协同过滤推荐方法，降维的同时利用本体论提高推荐的准确性[11].王运等在传统的概率矩阵分解算法基础上，利用用户项目评分数据及项目信息提出了融合用户偏好和项目相似度的概率矩阵分解推荐算法，虽没有根本降低矩阵分解技术计算复杂度，但仿真实验表明该算法获得了更好的评分预测准确性[12]，一定程度上缓解了该类方法推荐失真的问题.但由于奇异值分解的复杂度，计算耗时较长[13].

2.4 基于评分预测的矩阵填充

对用户未评分项目进行评分预测，回填到评分矩阵中进行协同过滤推荐，个性化程度和精确度都有所提高[14].缺省值预测常用的方法如下：使用N个近邻用户对项目i的平均评分作为用户u对未知项目i的预测评分P(u，i)[15-17]，这种方法将近邻用户同等对待，忽视了不同近邻用户特征对预测评分的贡献程度的影响，大大降低了预测结果的个性化程度.彭石等提出一种基于加权Jaccard系数的综合项目相似度度量方法[18]，使用项目综合相似度对评分矩阵进行填充，但是项目属性的选取没有统一规则，所以可靠性和普适性不强;卢棪提出了一种以迭代的方式进行缺失值预测评分矩阵填充方法[19]，这种方法在每一次迭代中仅考虑项目间的相似度来生成预测评分.

向小东等使用Slope-One算法计算得到的评分预测值来填充评分矩阵中的未评分项目，该方法有效地降低数据稀疏性，相比其它方法算法简单，易于实现，执行效率高[20]，但依然只从项目相似度角度进行未知项目的评分预测;刘林静等提出了一种基于用户相似性的加权Slope-One 算法，将用户间的相似性作为预测评分权重[21]，但去除评价次数小于0.01%的极度不活跃用户仅考虑活跃用户的影响作用，失去了一定的有效信息;张玉连等提出的加权Slope-One算法在预测评分时进一步考虑了不同项目的用户评论数量差异的影响[22];李桃迎等则针对Slope-One算法未考虑用户兴趣变化和用户相似性的问题，提出了基于用户兴趣遗忘函数和用户最近邻居筛选策略的改进方案，以期提高推荐的质量[23];王卫红提出基于用户自身属性的加权Slope One算法，将用户对项目类别的评分添加到评分矩阵以降低数据稀疏性的同时，在计算用户间相似度时考虑了用户年龄、性别和职业等属性，提升了推荐准确性和算法可拓展性[24].但无论是基于用户相似性还是考虑用户自身属性的加权Slope-One算法，用户-项目评分中仍然忽略了用户话语权这一重要用户本身属性的影响.

2.5 综述小结

用户/项目聚类和用户/项目相似度计算改进两类方法并没有根本解决数据稀疏性问题本身，且存在部分丢失或忽视最能反映用户偏好的用户/项目信息、过于依赖用户/项目特征数据等缺陷;基于评分预测对用户-项目矩阵的缺失数据进行填充的矩阵填充法，克服了SVD等矩阵降维方法计算复杂的缺点，近年来引起了学术界和企业界的关注.因此，本文拟对矩阵缺省项预测的Slope-One算法和现有的加权Slope-One算法原理及局限进行分析，在考虑评分用户数量不同对于计算项目评分偏差影响的同时，充分考虑用户属性的不同对于评分预测的影响，提出一种兼顾用户话语权这一重要用户属性的改进的加权Slope-One算法，以期在解决数据稀疏性问题同时进一步提升评分预测的精度.

3 Slope-One算法的局限

3.1 Slope-One算法的原理

Slope-One算法是一个增量算法，基于该算法的协同过滤推荐对评分很少的用户也可以产生推荐，并且精确度比基于用户和基于项目的协同过滤推荐算法的表现要好[20，21]，Slope-One算法核心的思想是根据所有用户对项目的评分推算出项目集合中两两项目之间的评分差值，从而根据项目之间的评分差值和用户已有的评分记录来近似地预测该用户对目标项目的评分.

下面用一个简单的例子来阐述Slope-One算法的原理.假设有U1、U2、U3、U4、U5这5个用户分别对I1、I2、I3、I4这4个项目的评分记录，如图1(a)所示，其中：“-”表示未评分，“？”代表需要预测的评分.

原始的Slope-One算法预测用户U1对项目I3评分的流程如下：

Step 1.筛选用户集合.

先筛选出对目标项目I3进行过评分的所有用户的集合，即{U2，U4，U5}，如图1(b)所示.

Step 2.筛选项目集合.

在用户集合{U2，U4，U5}中，寻找与目标用户U1同时进行过评分的所有项目，包括目标项目在内构成项目集合{I2，I3，I4}，如图1(c)所示，从而锁定Slope-One算法所需要的用户-项目评分数据.

图1 Slope-One算法原理示意图Fig.1 Schematic diagram of Slope-One algorithm

Step 3.预测目标项目评分.

项目j与项目i的评分偏差devj，i如公式(1)所示：

(1)

用户u对项目j预测评分P(u)j如公式(2)所示：

(2)

其中：Uj，i表示同时对项目j和i评过分的用户集合;Ij表示用户u所有已评分且满足条件(i≠j∩Uj，i≠φ)的项目集合;ru，i和ru，j分别表示用户u对项目i和j的评分;card()表示集合中的元素个数.

3.2 加权Slope-One算法及局限

原始的Slope-One算法中，项目之间共现的次数无论是多少，最终考虑的都是平均评分差，那么考虑项目之间共现次数的影响.对于项目i和j来说，在计算评分偏差devj，i的时候并没有考虑评分用户数量差异对devj，i可信度的影响，假如有1000个用户都给项目i和j打了分，而只有一个用户给项目i和k打分，那么devj，i的可信度是要远远高于devj，k的.在此基础之上，加权Slope-One考虑了共现次数，项目和目标项目共现次数越多，所预测的得分置信度越高.

加权Slope-One算法考虑到两两项目之间共现次数即不同的评分用户数量对于计算项目评分偏差时的贡献不同，对不同项目计算得到的平均偏差进行加权，改进后的计算如公式(3)所示：

(3)

其中，card(Uj，i)是对项目i和j都做出过评价的用户数量.

加权Slope-One算法在原始的Slope-One算法基础上既考虑了项目平均评分差异，又针对项目的评分用户数量进行了加权处理，通过用户评分数量的加权得到项目之间的评分偏差的加权平均，从而克服了原始Slope-One算法在项目的评分预测中不同项目的评分用户数量差异对评分偏差的影响[21].

但是传统的加权Slope-One算法仍然是基于项目考虑评分用户数量的差异，却忽略了用户本身属性尤其是不同用户活跃度差异的影响.比如，用户a评论总数是2000次，而用户b只有20次，两个用户的活跃度不同，活跃度越高的用户，对于推荐系统中同一项目评分预测的贡献越大，意味着该用户的话语权越高.因而，传统的加权Slope-One算法忽略了用户话语权的作用，限制了评分预测的可信度，进而一定程度上影响基于该算法的协同过滤推荐的准确性.

4 基于改进加权Slope-One的协同过滤推荐算法

4.1 兼顾用户话语权的加权Slope-One算法

本文在传统的加权Slope-one算法考虑不同项目之间评分用户数量差异影响的基础上，进一步考虑了不同活跃度用户的话语权差异对评分预测的影响，提出改进的加权Slope-One算法.

作为协同过滤推荐算法重要输入的用户-项目评分矩阵，评分次数不同的用户，其活跃度存在差异，对评分预测的话语权显然不能等同对待，充分考虑用户话语权的大小对评分偏差的影响，可以有效避免出现爱好大相径庭的用户被计算为相似用户的问题.当然，为了避免人为刷评论或者恶意评论等行为的影响，需要对用户-项目评分数据进行有用性甄别.以一个例子说明如下：假如现在用户U2，评分次数为100，他对于项目I2和I3的评分分别是2和5，I2和I3的共同评分用户数是30;另一用户U4，评分次数为20，其对项目I2和I3的评分分别是5和2，I2和I3的共同评分用户数是50;而用户U5的评分次数是50;其他的用户-项目评分同图1，那么，根据加权Slope-One算法首先据公式(1)计算项目I2和I3、项目I3和I4的评分偏差分别是：

如果考虑用户评分数量差异作为权重，项目I2和I3、项目I3和I4的评分偏差则分别是：

显然，考虑用户话语权有利于消除了加权平均评分差所带来的偶然因素导致的加权评分差为0的现象，这个方法也大大降低了由于偶然因素导致的爱好不一样的用户被计算为相似用户的概率.因此这种基于用户话语权的加权Slope-One算法总结如公式(4)和公式(5)：

(4)

(5)

其中，Nu代表数据集中每个用户的评分次数，它反映了用户活跃度.

4.2 基于改进加权Slope-One算法的协同过滤推荐流程

针对协同过滤算法中数据稀疏的问题，本文在传统加权Slope-One算法基础上提出了考虑用户话语权的改进算法，用户活跃度越高则对项目评分的话语权越大.据此对用户未评分项目进行预测以实现用户-项目评分矩阵的填充，作为协同过滤算法的输入.

U为用户集合，I是具有预测评分的候选项目集合，M0是用户-项目初始评分矩阵，Mi为用户-项目填充后的评分矩阵，N为给每个用户推荐的项目个数，L0是初始候选列表，L1是候选列表，Len(ui)为用户评分列表填充长度，L(u)为给所有用户的最终推荐列表，则基于改进加权Slope-One算法的协同过滤推荐流程描述如图2所示.

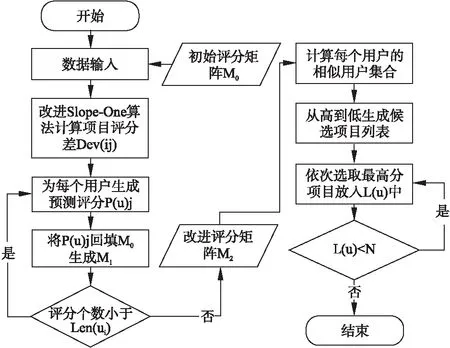
图2 基于改进的加权Slope-One算法协同过滤推荐流程Fig.2 Flow chart of collaborative filtering recommendation algorithm based on improved weighted Slope-One algorithm

5 仿真实验

5.1 实验数据

本文仿真实验选取了稀疏度不同的两个数据集Movie-Lens和Amazon-Clothes作为实验数据.Movie-Lens数据集是由明尼苏达大学的Grouplens团队收集的真实电影评分数据，经清洗得到了包含943个用户对1682部电影共100000条有效评分数据，其中每个用户至少对20部电影进行了评分，平均评论数为106次.Amazon-Clothes数据集由加州大学Julian McAuley教授团队收集的亚马逊服装销售的真实评分数据，经清洗得到了包含6962个用户对5000个项目的226956条有效评分数据，平均评论数33次.两个数据集的评分值均为1～5之间的整数，数值越高用户满意度越高.

借鉴文献[21]关于数据稀疏度的计算方法，Movie-Lens数据集的稀疏度为0.937，相对较低;Amazon-Clothes数据集的稀疏度为0.9934，相对较高.

本实验主要目的是验证本文提出的基于改进评分矩阵填充算法的协同过滤推荐的准确性.采用五折交叉法，将数据集随机分为5个不相交的子集，每次实验选择其中一个子集作为测试集，其余的4个子集作为训练集，如此重复5次的平均结果作为最终结果.每个数据集的4个训练集用于本文算法计算用户对项目的预测评分，而测试集则不参与预测评分，仅用于评估本文算法的推荐效果，之后将预测评分与实际评分进行MAE值的比较.

5.2 仿真对比的算法和指标

基于奇异值分解(SVD)的协同过滤算法通过降维来减小数据稀疏性的影响[7，8]，因此作为仿真对比的算法之一;其次，选择原始的协同过滤算法和基于传统加权Slope-One的协同过滤算法，作为本文基于改进加权Slope-One的协同过滤算法的对照组.

本文采用调整余弦相似度(Adjusted Cosine Similarity)[6]计算相似度;采用平均绝对偏差MAE(Mean Absolute Error)作为推荐准确度的评价指标，对比上述4种算法在两个不同稀疏度的数据集Movie-Lens和Amazon-Clothes上的MAE表现.MAE越小，算法准确性越高[1].

5.3 确定最优填充比例

按照Slope-One填充的评分矩阵，先通过仿真实验1来得到最优的填充比例，即对每个用户填充的预测评分数目，来验证矩阵填充比例变化对本文算法的绝对误差的影响，实验1中，矩阵填充比例分别取10%、20%、30%、40%、50%、60%，70%.本文改进Slope-One算法在Movie-Lens数据集和Amazon-Clothes数据集上的MAE值表现如图3所示.

图3 不同填充比例下本文算法的MAE值表现Fig.3 Comparison of MAE values of proposed algorithm under different filling ratios

由图3可知，本文算法在Movie-Lens数据集上的表现要好于在Amazon-Clothes数据集，同时本文算法在两种数据集上的MAE值均在填充比例在30%左右趋于稳定，因此后续实验中本文算法填充比例将采用30%.

5.4 确定最优近邻数

采用最优填充比例30%使用本文改进加权Slope-One算法对两个数据集的评分矩阵进行填充，然后分别使用另外3种算法对2个数据集进行仿真实验2确定近邻数N的大小.在实验2中分别取N=10，20，30，40，50，60，70，80，90，观察近邻数的多少对推荐准确性的影响.如图4所示，整体而言，对于4种算法，随着近邻数的增大，MAE 值逐渐降低，并在N= 50 时逐渐趋于稳定，因此，最优近邻数目选择50.

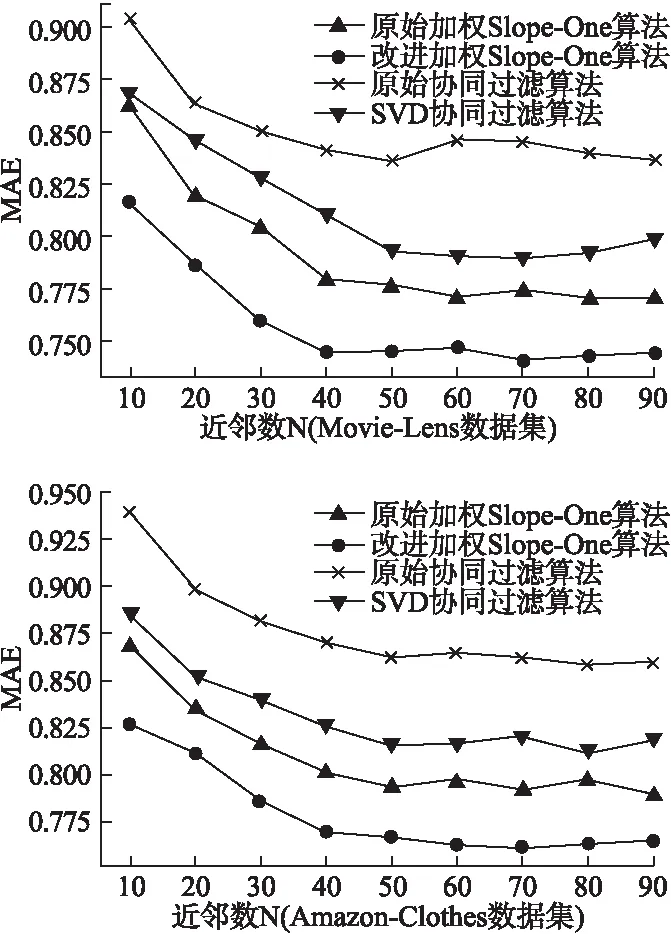
图4 不同近邻数下4种算法MAE值对比Fig.4 Comparison of MAE values of four algorithms under different neighbor numbers

5.5 仿真结果分析

对4种算法进行MAE值仿真对比实验3，结果如图5所示.

由图5可知，从算法精度来看，4种算法中，本文算法在不同稀疏度的两个数据集上的平均绝对误差值都表现最佳;表现其次的是基于SVD的协同过滤算法和原始加权Slope-One算法;原始的协同过滤算法表现最差.表明本文算法相对其它3种算法能够更有效地降低数据稀疏对推荐准确度的影响.

图5 4种算法在2个数据集上的MAE值对比Fig.5 Comparison of MAE values of four algorithms on two datasets

从数据集角度来看，各算法在数据稀疏度略高的Amazon-Clothes数据集上的总体表现都略微比Movie-lens数据集差，说明稀疏度的升高的确会影响算法的准确度;SVD协同过滤算法和原始的加权Slope-One算法在Amazon-Clothes数据集仿真中的表现差别不大，但是在Movie-lens数据集仿真中，原始的加权Slope-One算法明显要比SVD协同过滤算法表现好，说明基于原始加权Slope-One的协同过滤推荐算法在稀疏度较低的数据集上相对SVD略有优势一些;本文提出的基于改进加权Slope-One的协同过滤推荐算法在不同稀疏度的数据集上的仿真中表现稳定且都相对最优，进一步验证了本文改进算法的优越性.

6 结束语

针对目前基于内存的协同过滤算法中数据稀疏性导致的推荐结果准确度不高的问题，本文在加权Slope-One算法基础上提出了兼顾项目之间差异和用户之间差异的改进算法，在对用户-项目评分矩阵进行填充预测时考虑用户话语权的影响;并通过仿真实验确定了该算法的最优填充比例和最优近邻数等重要参数，有效缓解数据稀疏性的同时，确保用户-项目的评分预测最大限度地体现用户相似性.基于Movie-Lens和Amazon-Clothes两个不同稀疏度数据集的仿真实验显示，相对于经典协同过滤算法、基于SVD的协同过滤算法以及原始加权Slope-One算法3种算法，本文提出的基于改进加权Slope-One的协同过滤算法的推荐结果的MAE值最低.

为了揭示4种算法在不同稀疏度数据集上的表现和适用性，本文采用的两个数据集的稀疏度差别还不够突出，今后将会尝试在稀疏度反差更大的若干个数据集上分别验证4种算法的性能表现.