一种基于时不变稳定性和夏普比率的模型泛化能力优化方法

邓洪武，邢 凯，王志勇，李亚鸣，胡 璇

(中国科学技术大学 计算机科学与技术学院，合肥 230027)

(中国科学技术大学 苏州高等研究院，江苏 苏州 215123)

E-mail：denghw@mail.ustc.edu.cn

1 引 言

近年来随着深度学习在计算机图像识别领域的快速发展，深度学习及多种预训练模型被广泛应用在多类高价值应用场景，比如安防监控，自动驾驶与智能医疗等.对于多类指定图像识别任务，近几年出现的深度学习预训练模型性能已大幅超过了传统图像识别模型.这主要得益于3个方面：信息化时代产生的大规模数据集、满足计算要求的海量算力，以及高效的算法.

尽管深度学习预训练模型在图像识别领域的指定任务上已取得了比传统模型更加优异的成绩，但它在进一步广泛应用之前，仍然有很多挑战需要解决.首先，如何提高模型的泛化能力是深度学习预训练模型能否广泛应用的关键[1].目前图像识别领域的深度学习模型一般都是基于监督学习[2]，即先在已知标签的数据集中进行训练然后再应用.但是图像识别的应用场景与其训练场景往往并不相同，即训练集和测试集的数据分布不同，很多测试/应用场景在训练集中并没有出现过，因此要求模型具有较好的泛化能力.其次，如何获取并合理利用数据集是构建有效模型的前提.深度学习模型一般需要大规模数据集进行训练，但是大规模数据集往往是难以获得的，导致很多本应有效的算法在数据量不足时难以达到较好的效果.另一方面，如何利用超大规模数据集达到算法的极限性能也是应用的重要需求，比如在自动驾驶和智慧医疗的应用场景中，数据集往往易于获得，但是算法出错的成本非常高，一般需要对噪音/干扰具有良好鲁棒性的模型.

针对上述研究挑战，学者们在当前研究中提出了多种解决思路.考虑到深度学习模型通常是基于梯度下降算法得到，但是其优化空间十分复杂，难以优化且易陷入局部极小值.因此对于该类情况的针对性优化可以缓解这种问题，比如Adagrad[3]根据梯度动态调整学习率，Momentum[4]借鉴动量的思想，积累之前状态的动量来代替当前梯度.Adam W[5]为了缓解过拟合现象，在模型中加入正则化.Demon[6]基于迭代进度来调整momentum参数以提升优化算法的性能.虽然这些方法在不同程度上都提升了模型的表现，却并没有解决梯度下降算法的根本问题，其模型泛化性能始终存在理论上的缺陷.

针对数据集规模问题，当前研究通常是对通用数据集进行数据增强，或是利用元学习[7-9]，或是对模型添加先验信息的方式[10]，以此来从较少样本中学习到较好的模型.这些方法都在一定程度上提升了模型的泛化性能，但仍然对数据规模/先验信息提出了一定要求.针对小样本数据的问题，基于监督学习的训练方式仍然面临较大挑战.该领域的研究仍需要进一步从分布角度而非样本层面来对模型和相应的学习过程进行处理，以做到更好的概念层次的泛化.

针对深度学习预训练模型的泛化能力问题，近期研究中学者们进一步提出对深度网络结构和参数进行优化的思路，以此来提高模型对不同数据分布的泛化识别能力.比如利用随机dropout[11]来尝试找到更好的参数和结构，或是通过改良激活函数如Swish[12]使得模型在优化时可能跳出局部极小值，Mish[13]在此基础上通过设计更平滑的激活函数使得模型泛化性能进一步提升.何凯明提出的动量对比(MoCo)[14]是一种通过使用对比损失将一个已编码的查询与一个已编码的键词典进行匹配来训练一个视觉表征编码器的无监督学习方法.SinGAN[15]是一个可以从单张自然图片学习的非条件性生成式模型，模型采用多个全卷积GANs组成的金字塔结构，每个层级的网络学习了图片上不同位置和尺度的分布信息.目前该方向的进展多聚焦于特定模型的网络结构/参数优化，亟需一种网络结构优化的高效的通用指导方法.而同样针对不同尺寸的物体，Wang等人[16]提出了FPN通过多尺度信息融合增加模型泛化性能.而SOLO[17]的核心思想是将实例分割问题重新定义为类别感知预测问题和实例感知掩码生成问题，将实例分割问题转化为逐像素的语义类别分类任务.

此外，在图像识别领域中，基于深度学习的特征提取通常是采用卷积神经网络[18]，但不可避免的，特征图中会存在很多与主体特征无关的信息.这些噪声信息不仅会影响特征提取器的性能，导致模型性能变差，易受干扰，还会消耗过多的算力.因此如何识别有效信息并构建高效的特征组合，也是提高深度学习网络泛化性能的关键.

另外就当前的深度学习模型来看，用于特征分类的网络结构，如全连接层和池化层还存在可解释性不强，特征分类意义不明确的问题[19].针对以上问题，本文通过时不变稳定性和调制干预对模型特征提取结果进行去噪，筛选出有意义的节点，然后利用夏普比率和注意力机制对中间数据进行组合，生成和数据分布密切相关，具有概念层次含义的具有可比较性的特征，并进行分类.

本文从分布的角度对网络节点进行评价，通过时不变特性对模型进行去噪，同时利用夏普比率可以计算最优投资组合的特性，设计独特的收益函数，将低维特征组合为高维特征，并结合注意力机制生成概念层次的特征.本文创新点如下：

1)基于时不变稳定性从分布角度对网络结构进行分析并筛选具有时不变稳定性的子结构.

2)通过与分布相关的Wasserstein度量来构造收益函数，引入夏普比率来选择性构建神经元聚合子结构实现特征生成.

3)基于所生成的弱/去相关性的有效特征，通过注意力机制构建概念层次的embedding表征.

本文的内容组织如下：第2部分主要描述本文采用的技术，第3部分讲述研究内容及实验设计，第4部分是本文实验设计的工作原理及理论推导，第5部分详述实验结果及结论，最后第6部分进行总结与展望.

2 相关工作

2.1 深度学习模型时不变稳定结构

模型的时不变稳定性[20]是指在输入端改变输入时间时输出端只会改变输出的时间而不改变输出值的特性，因此模型需要满足叠加性和均匀性，并且参数不随时间改变.Sain的研究表明[20]，时不变稳定的结构在受到有界扰动的时候，即使其初始偏差很大，只要后续取消其扰动，模型都能够最大限度地恢复到初始的平衡状态.图像识别的工作类似于对图片去噪，获取本质的信息，而具备时不变稳定结构的图像识别模型可以在存在噪声的情况下经过一定的信息处理恢复本质特征.深度学习时不变稳定结构的发现需要借助因果干预手段.由于时序数据的获取难度很大，本文采用基于非时序的因果关系，通过添加调制的干预生成数据，进而挖掘具有因果性的时不变稳定子结构.

Pearl的研究[21]表明，深度学习模型在具有比较确定的因果性时泛化性能优良，而Pearl认为，因果性分为3个层次：相关性、干预和反事实推理，由于目前的卷积神经网络的构建基础为相关性，导致其性能存在理论上的上限，因此只有提高因果性的层次才可以达到更高的泛化性能.在相关性的基础上，对模型提出更深层次的要求，如果模型受到干预时节点比较稳定，模型结构就满足了第2层次的要求，而这种模型结构就是时不变稳定结构.

2.2 Wasserstein度量

Wasserstein度量[22]可以描述两个分布之间的距离，定义两个概率测度之间的Wasserstein距离为：

(1)

其中X～μ，Y～γ为在概率空间Ω上的任意两个概率测度，d(x，y)为概率空间上的一个度量.

根据上述定义，Wasserstein度量实际上刻画了两个概率测度或者实际情况中两个样本分布之间的距离表征，可以表述为从一个分布转化到另外一个分布所需要的代价.本文中之所以采用Wasserstein距离，是因为其作为一个距离度量来说是对称的，并且在两个分布距离较远甚至毫无重合区域时仍然可以度量两种分布之间的差别，不会出现梯度消失的情况，这有助于我们计算距离并进行优化.

2.3 夏普比率

世界有一个基本规律：收益越高、风险越高，当一个产品收益很高但是风险很低的时候，一定会有很多资本进入导致平均收益降低.在深度学习中，模型需要确定每个特征的重要性并分配权重，从而逼近正确结果，这与构建最优投资组合有异曲同工之妙.夏普比率[23，24]可以通过计算收益与风险的关系，获取单只股票的投资比重，因此可以将夏普比率应用到神经网络权重计算上.如图1所示，市场中所有的风险证券的市场组合会构成一个可行区域，而投资者会从这些可行区域中选择最优的市场组合.

图1 夏普比率Fig.1 Sharpe ratio

图1中，曲线表示有效前沿，在未考虑无风险收益的前提下，有效前沿上半曲线上的点都是市场最优证券组合.当无风险收益介入时，曲线中存在某个点能达到最大收益，此点的斜率为夏普比率，此点为夏普比率最大的点.当无风险收益介入的时候，可将曲线上的每个点与无风险收益点进行连接构成资本配置线，当资本配置线与有效前沿相切时夏普比率最大，此时资本配置线被称为资本市场线，切点为存在无风险收益时的最优市场组合.资本市场线的公式为：

(2)

其中RA表示市场组合A的收益，σA和σP分别表示市场组合A和P的标准差，rf表示无风险资产f的收益.经过无风险收益点的最大斜率资本配置线其斜率即为夏普比率：

(3)

夏普比率又称报酬-波动性比率，刻画了投资组合每多承担一单位总风险时所获得的超额报酬，在给定标准差的情况下，夏普比率越高的投资组合其在同样风险下拥有更高的期望收益.

2.4 ResNet预训练模型及相关深度学习图像识别方法

超大规模数据集和超大算力处理器的出现使得深度学习在新时代得以大展拳脚，各种高效的深度学习模型层出不穷.LeCun等人[25]提出了 LeNet-5 网络，此网络包含了深度学习的基本模块：卷积层、池化层和全连接层，通过两次卷积和池化提取特征，再使用三层全连接层对特征进行分类.LeNet-5网络在手写数字识别任务中达到了99.2%的分类准确率，证实了卷积神经网络在图像分类任务中确实存在优越性.但是LeNet-5存在训练数据集规模小、泛化能力弱、训练开销大的缺点.为此，Krizhevsky 等[26]提出了AlexNet 网络，主要是使用了 ReLU 激活函数代替Sigmoid，从而解决网络较深时的梯度弥散问题，使得梯度下降的速度进一步加快；同时引入 Dropout 技术，降低网络的过拟合程度，降低训练模型计算量.Simonyan 等[27]提出了 VGG 网络，通过反复堆叠 3×3 的卷积核和 2×2 的最大池化层，实现了16～19层的卷积神经网络.网络采用多尺度训练策略增加了数据量，证明了在一定程度上，神经网络越深，效果越好.由于更深的网络和更小的卷积核带来的隐式正则化效果，VGG只需要较少的迭代次数就可以收敛.VGG 网络在图像分类和物体定位任务上都取得了很好的效果，但网络深度的增加会带来训练误差增大的网络退化问题.

He等[28]提出了ResNet 网络，解决了深层网络训练的退化问题.ResNet 通过残差模块，设置恒等映射增加模型的深度.ResNet的结构可以极快地加速超深神经网络的训练，并且模型能够达到很高的准确率.ResNet网络的出现，使得构建超深层网络成为现实，网络的深度目前可达到1000层以上，对卷积神经网络的后续发展有着深远的意义.

Szegedy 等[29]为了优化卷积神经网络结构，降低网络复杂度，提出了 GoogLeNet网络.网络深度为22层，由若干Inception模块级联而成，采用全局平局池化层替代最后的全连接层，增加辅助分类节点，最终以 93.33%的Top-5准确率获得ILSVRC 2015比赛分类任务的冠军.Inception 模块通过使用多种不同的卷积核提取不同层次的特征，然后综合特征进行预测.同时，1×1 的卷积可以用很小的计算量增加一层特征变换和非线性化，不仅可以改变输入输出的维度，并且可以将不同通道的信息进行融合，增加特征之间的互信息.Huang等人[30]使用比ResNet更密集的短路连接，进一步扩展了Shortcut的思想，不仅进一步缓解了梯度消失的问题，促进了特征重用，还降低了模型的参数量.

3 基于时不变稳定性和夏普比率的ResNet泛化能力优化方法SR-Net

本方法由3部分组成：1)首先采用ResNet预训练模型作为基础网络，通过基于时不变稳定性的网络结构定向选择性dropout对模型进行去噪；2)进而利用Wasserstein度量和夏普比率选择性构建神经元聚合结构来获取高维抽象特征；3)在此基础上，利用注意力机制和全连接层提取具有概念层次意义的embedding表征，生成泛化模型.

3.1 基于时不变稳定性的网络结构定向选择性Dropout

ResNet等预训练模型由卷积层和分类层构成，其中卷积层作为图像领域最常见的特征提取网络，由全连接网络通过局部采样和权值共享改良而成.工作原理是基于局部数据构建局部特征，基于底层局部输出进一步构建高维抽象特征.但是对于卷积神经网络来说，其特征提取结果是冗余的，往往存在噪声背景特征.如果采用这些特征直接进行图像分类，结果显然不是最优的.因此，如何识别出有效的输出并进行处理，成为提高深度学习网络泛化性能的关键.筛选有效中间输出的原理是：根据Mellor J等人[31]的实验结果，当数据变化的时候，其损失函数相对于输入数据的雅可比矩阵可以看成一个长向量，性能越好的结构，在不同数据之间，其雅可比矩阵越不相关.

基于Pearl的理论[21]，模型具有良好泛化能力的前提是其存在比较明确的因果关系，而由于卷积层的构建基础为相关性，因此其中不稳定的节点会受到噪声的影响.对于同样的卷积核，如果具有相同本质特征的同类图片输入，其输出的分布如果较为稳定，则不易受噪声/干扰影响；反之，易受噪声/干扰影响的节点的输出分布是不稳定的.同时Pearl提出，因果性分为3个层次：相关性、干预和反事实推理，因此如果模型受到干预时节点比较稳定，模型结构就满足了第2层次的要求，也就能筛选出其中以因果性为基础而实现的子结构，进而实现泛化能力的优化.因此本文采用干预调制的方法将原有的非时序数据生成序列数据，对模型输出结果进行评价，进而评价网络模型结构，指导模型生成.本文采用Wasserstein距离对数据分布进行度量，而数据分布与调制曲线的关系采用因果关系检验进行检测.

干预调制可采用多种不同的方式，例如采用调制的高斯模糊函数：

(4)

干预调制的步骤设计如下：

1)对于多个不同的样本进行相同的调制序列干预，每个样本生成多张不同的图片；

2)获取模型特征提取层的结果，其维度是[样本数，数据增强个数]；

3)将采样点输出作为分布，找出此分布与调制曲线的关系以及采样点之间的关系.

通过两种筛选标准对模型结果进行去噪：1)同类样本添加背景噪声，选择Wasserstein距离分布稳定的节点；2)同类样本添加主体调制噪声，选择模型输出结果与调制曲线存在因果关系的节点.针对时间序列上的数据分布与原始调制序列之间因果关系的检测，采用协整检验[32].

3.2 基于Wasserstein距离和夏普比率选择性构建神经元聚合结构

Ruder等人[33]的研究显示，在高维空间中直接采用梯度进行数值优化存在一定的局限性，而从分布角度[34]则比较稳定，所以本文采用分布角度的优化替代梯度下降.而在高维空间的高维曲面上找到合理的分布则需要借助最优传输距离，通过找到最有效的传输路径获得合理且高效的优化方法.采样获得的特征图与高维空间上物体本质的分布表达存在距离，而如何进行有效逼近就是特征解释函数的作用，也就是希望找到每个特征与最优表达之间的最优传输路径[35，36]，我们采用Wasserstein距离进行衡量.确定度量方式与特征采样分布后，就可以采用夏普比率构建最优资产组合.

通过第1节中筛选有效节点的步骤，我们去除了CNN卷积结构中易受噪声/干扰影响的点.然后对每个点选取与其负相关性高以及一部分不相关的采样点并将其作为一个整体，采用协方差矩阵并借鉴夏普比率获取整体的最优组合.使用夏普比率从采样点构建特征时，需要定义采样点的收益以及风险.通过筛选节点的标准可以得知，采样点类内的分布距离应该尽可能小，而类外的分布距离应该尽可能大，因此定义收益为类外距离与类内距离的比值，这也是模型定义的优化目标.因此单个节点构建的收益函数定义为：

(5)

其中WI表示类外的分布距离，WB表示类内分布距离，构建数据的时候，将每个类内数据分布作为标准，然后计算其他类外数据分布与其分布的距离.选择类外的图片时，每个类别选择相同数量的图片，并对分布取平均，增加类外多样性.然后将不同图片作为标准，可以得出对应的新节点，最后对类内数据取均值，增加类内多样性.当获取的数据分布有类内多样性和类外多样性之后，就可以构建类间Wasserstein距离大，类内分布趋同的稳定特征，这些特征可以增强每个类和其他类的可区分性.这样通过夏普比率最优组合之后的特征具备高收益低风险(即夏普比率高)的特点.

从采样点集合构建出特征点之后，通过stacking最优组合结构构建单分类概念层次的表示，选择性生成具有高夏普比率的聚合结构.上一节中对于每个采样点，构建了属于特定特征的最优结构，对于结构生成的特征，我们从同样的角度出发，用基于夏普比率的选择性池化与连接的思想对特征进行组合，构建概念层次的表示.首先选择比当前收益大的特征点，然后通过协方差矩阵筛选相关性高的特征，对所有这样的整体构建最优组合.通过多次堆叠这样的结构，不断增加收益，降低风险，获得的特征图就是单分类概念层次的表示.

3.3 基于注意力机制的多分类泛化模型生成

单分类概念层次的表示具有相对稳定的偏序关系，但针对不同类别，其偏序关系并不相同.若要构建绝对稳定的高维分布，需要统一其偏序关系，而自注意力机制[37]恰好可用于沟通各类表示之间的互信息，达到多分类问题所需的通用概念层次表征.因此从不同类中构建相同偏序关系的表征，进而增强模型的泛化性能.每个类别都通过夏普比率层构建了属于其自身的独特特征向量，但是，如果将所有的特征向量直接连接，其中间结果没有互信息的辅助，难以得到较好的结果，因此，我们加入注意力模型.通过实现自注意力机制进一步增强模型的泛化模型生成，计算出最终的特征向量.这种做法比较类似Inception的思想，不再加深模型而是扩展模型的宽度，通过每个类别单独处理特征，再组合特征形成特征向量进行分类.

通过特征组合获得单分类概念层次的表示之后，我们采用多头注意力模型增强特征向量之间的互信息.如图2所示，自注意力机制通过计算单类别向量与整体语义空间的关系来调整每个类别的分布，进而使用多头注意力机制使得模型可以在不同的表示子空间中学到更多的互信息.对于不同类别单概念层次的表示向量，通过不同的初始参数构建多组特征向量Query、Key以及Value，对于同组的向量，通过一系列操作计算向量自身的相关系数，并通过对原向量进行系数加权构建更有效的特征向量.自注意力机制利用多个向量之间的语义空间关系对比获得更加准确的空间特征向量，借此生成多分类概念层次的表示，用于后续embedding表征的生成.

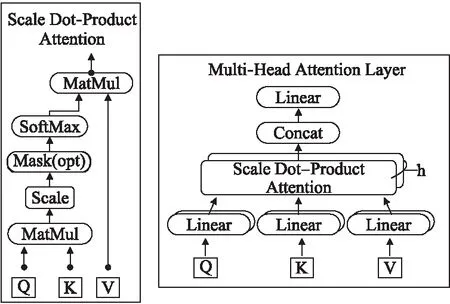
图2 自注意力机制Fig.2 Self-attention mechanism

3.4 概念层次的embedding表征与泛化模型生成

通过前述过程，我们构建了每个类别的特征向量，其在高维空间分布稳定且分类准确率高，并且相当于在分类层生成了独热编码，但是独热编码的缺点在于无法完整表述类别之间的关系，因此希望生成有意义的embedding表征.前述过程通过去相关性我们分离了类别的高维表征，现在通过注意力机制加强类别之间的互信息.所以我们需要进行表征的转化，将独热编码转化为embedding表征.利用夏普比率及基于注意力机制的Transformer，每个类别在特征提取结果层的输出分布都是稳定且去相关的，这种形成了稳定分布的特征向量，我们称之为概念层次的embedding表征.通过比较多种类别的表征，可以看出在经过有效组合特征之后，利用余弦距离可以衡量类别之间的语义距离，也就是在同一语义空间形成了具有语义距离的特征表征.对于已生成的embedding表征，模型需要进行分类，通过直接连接注意力机制生成的embedding表征构成图片的特征向量，然后采用全连接层对特征向量进行分类.由于每个类别表征都形成了稳定的分布，因此模型的泛化性能好.

3.5 算法与网络结构

本文采用的模型总体架构如图3所示，图中4个部分分别表示串行的多个数据处理过程.图中第1部分是原始图像的特征提取过程，本文采用两种特征提取网络，分别是ResNet34和ResNet50的卷积层.卷积神经网络通过对图像进行层层迭代采样，获取高维抽象特征的分布，而不同的特征分布为下文提供了有效的资源.

图3 模型概图Fig.3 Overview of model

算法的重点在于第2部分和第3部分，通过对模型结构的有效筛选以及抽象特征的有效组合构建概念层次的特征.第2部分主要是通过因果干预判断模型中特征提取节点的性质，通过数据干扰构建图像序列，然后借助时不变稳定性检测和协整检验从数据分布角度出发，对深度学习预训练模型进行结构化分析，针对非稳定子结构进行选择性裁剪来实现网络修建.筛选出有效特征之后，第3部分对稳定的特征分布进行组合，构建出具有概念层次信息的高维抽象特征.主要使用的理论是夏普比率和注意力机制，夏普比率衡量的是特征组合的单位风险收益，而将收益定义为高维空间类内类外距离比值之后，最大化夏普比率就相当于最大化高维空间类别分布的类间距离同时最大化同类数据的聚集程度.算法通过有意义的组合特征，构建同一图片在不同类别的框架下的表现结果，通过去相关性找到单类的高维稳定分布，再借助注意力模型加强互信息，进一步增强高维空间分布的稳定性和同一语义空间的联系.经过上述关键步骤之后，模型已经得到了有意义的特征，而后续过程就是对特征进行线性分类，即第四部分.

4 理论分析

4.1 基于协方差矩阵和Hessian矩阵的基础原理分析

通过优化特征提取目标函数，我们需要借助目标函数的导数进行梯度下降，而通过Hessian矩阵从二阶导数的方向对模型直接进行优化正是目前最有效的优化方式[38].对于符合高斯分布的节点取值来说，我们可以证明Hessian矩阵等于其协方差矩阵的逆，因此我们可以通过优化协方差矩阵实现此目标，而夏普比率的目标与此不谋而合.通过利用协方差矩阵构建特征组合，最大化夏普比率近似于最优化Hessian矩阵.因此可以通过夏普比率理论生成有效特征.

在本文中，协方差矩阵主要有两个用途：首先通过协方差矩阵衡量节点之间的相关性，用于筛选节点；其次通过协方差矩阵近似Hessian矩阵的逆，借助夏普比率近似协方差矩阵进而实现最大化Hessian矩阵中每个单独分量的最大值，即最大化有效信息同时最小化噪声信息.

Hessian矩阵等于协方差矩阵的逆证明如下：

对于高斯随机变量θ，其期望为θ*，协方差矩阵为Σθ，因此其联合概率密度函数为：

(6)

因此优化的目标函数可以通过其负似然函数进行定义：J(θ)=-lnp(θ)

(7)

它是θ分量的二次函数，通过对θl和θl′进行部分微分，可以得到Hessian矩阵的分量：

(8)

因此：

(9)

即hessian矩阵可以通过协方差矩阵的逆进行近似.

4.2 损失函数关键性与基于夏普比率的最优解求解分析

深度卷积网络特征提取能力优秀，但是也会提取一些非主体特征，这些特征对目标的预测不仅毫无作用，还会徒增计算量，同时可能会影响最终模型的预测性能，因此我们需要对网络进行去噪.利用时不变稳定性筛选出每个类别对目标预测无意义的节点，将其进行置零，这样相当于对模型进行压缩[39].如果不进行此操作，噪声节点会影响数据的分布，导致无法进行有意义组合，并且后续筛选收益高的节点时，噪声节点可能收益会很高，但是对模型实际表现没有提升，甚至会影响最终效果，因此筛选深度网络时不变稳定结构很重要.

对于已定义的收益和风险，构建最优组合，我们可以直接计算出权重最优解，证明如下：

假设有N个风险资产，它们的收益率用随机变量r表示：

rN×1=[r1r2…rN]T

(10)

资产投资组合中它们的份额记为W：

wN×1=[w1w2…wN]T

(11)

设eN×1=[11…1]T，则有eTw=1，即所有投资份额的总和为1 .

则期望收益向量为：

E(r)N×1=[E(r1)E(r2)…E(rN)]T

(12)

协方差分量为：

σij=cov(ri，rj)=E[(ri-E(ri))(rj-E(rj))]

(13)

同时记协方差矩阵为V，对于某一投资组合p而言：

rp=w1r1+w2r2+…+wNrN

(14)

期望收益为：E(rp)=E(r)TW

此时我们的优化目标为在给定收益期望μp的情况下，最小化风险即：

(15)

在此我们假设V是正定矩阵，此时V的逆存在.构造拉格朗日辅助函数：

L(w，λ1，λ2)=wTVw-λ1(E(r)TW-μp)-λ2(eTw-1)

(16)

其中λ1、λ2均为拉格朗如乘子.使目标函数取得极值：

(17)

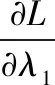
(18)

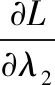
(19)

得：

(20)

(21)

(22)

记：[E(r)e]V-1[E(r)e]为A

则：

(23)

将此式代回原公式得到份额向量最优解：

(24)

根据上述的计算过程，我们可以准确计算出有效前沿的数学表达，同时将无风险收益定义为当网络结构随机初始化时的表现，表现通过收益函数定义进行衡量，据此，将节点分组后可直接计算出每个节点所对应的权重，并且根据上述理论，使用此权重组合特征的结果，其夏普比率最高.因此当我们确定收益和风险的定义方式时，我们就可以计算其特征合成的权重最优解.

4.3 概念层次的embedding表征与Wasserstein距离的相关性分析

通过时不变稳定结构的筛选之后，每个类别都获取了自身的特征图，但是通过特征图构建特征向量，我们需要对特征间的分布进行分析，通过特征相关性，构建高层次特征.对于每个类别的特征向量，综合进行预测.我们可以看作是目标特征向量的独热编码表示，但是如果仅仅使用这个独热编码进行分类，那么对于每个类别我们都需要实例进行训练，但是实际上我们并不能获得足够的数据集，因此我们需要借助一定的先验知识将独热编码向量转化为embedding表征，从而获得概念层次的信息表示.Embedding表征学习就是从数据空间自动学习出输入数据到统一目标表征空间的映射函数：

(25)

其中x表示独热编码，y表示embedding表征，通过给定约束条件constraint，从独热编码生成满足数据分布的embedding表征.而本节中，约束条件是对于多类图片而言，不同类别之间embedding表征应该相距较远，而同类之间则相对聚集.

我们通过Wasserstein度量衡量特征之间的相关性，在特征层次上，我们使用夏普比率组合特征，通过低维特征形成高维特征，进而进行预测.在数据层次上，我们通过Wasserstein距离度量分布距离，计算每个特征节点的收益与风险，并设计独特结构组合特征，得到单位风险收益最大化的特征.Wasserstein距离的优点在于作为距离，其具有对称性，且无论多大距离都可以有一个明确的表示，不存在优化过程中不可度量的情况.同时，由于此特性，在计算特征之间的相关性时，可以通过Wasserstein距离构建协方差矩阵和相关系数矩阵并参与计算.经过特征构建层后，每个类别形成了固定维度的特征向量，可以看作是每类的表示.

5 实验结果与分析

5.1 实验设置

为验证模型的有效性与泛化性能，采用ImageNet 2012[40]动物数据集作为标准数据集进行实验，部分实验结果均以ResNet-50作为基础网络，实验中采用100个动物类别作为实例进行详细分析.实验从准确率、召回率、训练数据规模以及特征泛化表现对模型进行评估.实验采用的数据集类别如表1所示，表中每个数据为ImageNet数据集中类别编号加类别名称.由于其数据分类很详细，为了讨论其泛化性能，本文在进行实验结果的展示时，考虑将其中的种类进行归纳，例如将多种不同的猫科动物全部统一为cat.本文的实验代码见(1)https：//github.com/wingsyu/SRNet.

表1 数据集列表Table 1 List of data

5.2 基于时不变稳定性的网络结构定向选择性Dropout的去噪性能分析

通过调制干预获得了原始数据特征提取之后的结果.对中间数据进行时间尺度上的分析，采用类内类外的Wasserstein距离进行评价，并通过方差对结果进行筛选，筛选之后，计算特征图中每个节点数据分布及信噪比提升情况，我们可以得出，平均信噪比提高3.72dB(约一倍以上).

经过前文提到的准则进行去噪之后，我们可以得到图4的结果.结果显示，在剔除噪声节点之后，几乎所有类别的召回率都可以达到较大程度的提高.从召回率的图示我们可以看出，通过数据分布稳定性对模型进行剪枝确实可以剔除非主体分布的无关噪声，进一步突出了主体特征的信号强度.在此阶段若不加本文的其他优化方法，直接采用预训练模型的全连接层，从最终结果可以看到模型召回率有明确的提升，并且每个类别的准确率也有小幅度上升，如果重新训练模型的分类层必然可以得到更好的结果.

图4 去噪效果示意图Fig.4 Denoising effect

同时为了验证模型的泛化性能，进行以召回率为唯一目标的网络特征节点的剪枝实验，得到如图5所示的结果，图中横坐标表示类别名称，纵坐标表示核心节点重合的数量，表格上方类别表示基准类别.从图5可以看出相似类之间的核心节点重合比较多，例如猫和猎豹；而不相似类之间重合节点很少，如猫和鱼，表明类间偏序关系存在的可能性，这将为下一步概念层次特征的提取建立较好的基础.

图5 不同类的时不变稳定性节点重合度Fig.5 Coincidence degree of different types of time-invariant stability nodes

5.3 模型性能分析

对去噪之后的有效特征进行生成组合后，其中间输出结果表明，基于所提取的有效特征，类间与类内距离几乎可以完全分开，并且多层堆栈连接之后效果可以不断提升.图6分别表示基于有效特征的各分类分布距离的差异情况，图中横轴表示网络中节点的序号，纵轴表示节点的类内与类外的距离.从图中可以看出随着有效组合，特征逐渐呈现类内外分离的趋势.

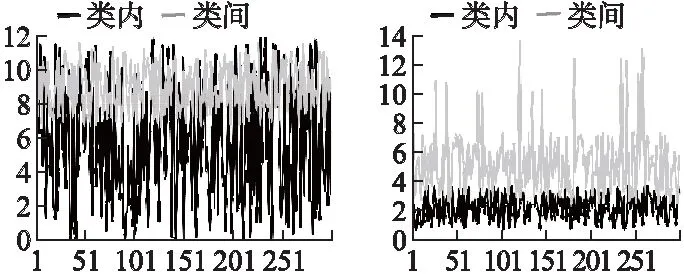
图6 类内类外分布距离示例Fig.6 Diagram of distribution distance inside and outside class

为了更好的说明问题，我们使用不同类别作为标准类进行实验，得到表格2所示结果.

表2中数据表示每个类的类内类外的Wasserstein距离值，通过实验结果可以看出，以任意一类作为标准类时，其他类别与该类的Wasserstein度量逐渐区分开来，并且使用ImageNet数据集中每类仅20张样本图片进行模型训练之后，改良之后的模型在ImageNet2012 100类数据集中准确率达到了86.72%，相对原始模型性能效果提升显著.

表2 特征组合效果Table 2 Effection of feature combination

表3显示了模型的性能表现，表中N表示模型特征提取网络的参数量，SR-Net表示本文所提出的模型.通过上表可以看出，我们的模型相对于传统ResNet耗费时间更少，训练集规模更小，但是由于删除了原始模型中的平均池化层，模型特征向量规模大，但是加入了注意力机制同时生成embedding嵌入表征，全连接层参数数量只和嵌入向量的维度相关，因此通过对每类20张图片进行增强扩展即可满足全连接层训练的数据量要求.

表3 模型性能比较Table 3 Model performance comparison

5.4 概念层次的embedding表征性能分析

通过基于夏普比率和注意力机制的泛化模型生成步骤之后，每个类别生成了其独特的概念层次的embedding表征，也就是特征向量.我们可以把这个特征向量看作是每个类别在统一目标表征空间的一种稳定表示，并且从数据分布角度看，类别内部特征分布稳定，类别之间距离较远.为了检验模型的泛化性能，我们采用表4中的数据进行实验.

表4 实验数据示例表Table 4 Sample table of experimental data

我们通过两种方式检验模型的泛化性能，首先是对于在训练集中已出现的类别但是未出现的图片，判断其准确率，由上文实验可知，准确率绝对值普遍提高约6%.另外，我们通过计算不同类别特征向量，对比了特征向量之间的余弦距离，得出图9所示的结果.

图7中圆点表示对比的中心类别，根据各类别的余弦相似度绘制了图7所示的示意图.图示结果显示，猎豹与同科的猫的特征向量余弦距离最小，而与同目的狗特征向量余弦相似度其次，其他的类别则距离较远，由此看出，模型在生成特征向量之后，其特征向量具有较稳定的偏序关系.

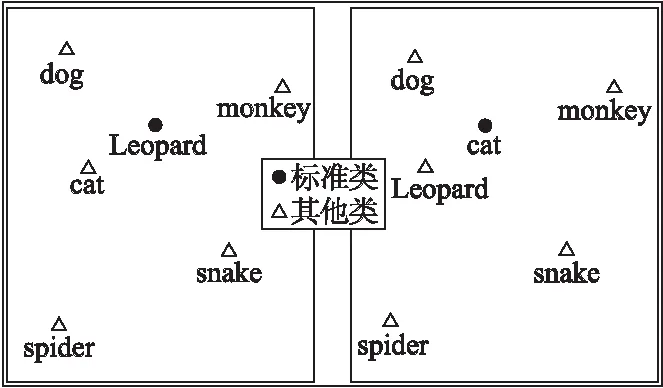
图7 特征向量余弦距离对比示意图Fig.7 Comparison chart of cosine distance of eigenvector

同时，对于未出现的类别，我们的模型可能存在一定程度的感知能力.具体来说，对于某个未出现的类别，我们构建其特征向量，并观察其特征向量与已出现类别的余弦距离.我们采用未用的豺类和湾鳄图片进行训练，豺类属于脊索动物门哺乳纲食肉目犬科豺属，湾鳄属于脊索动物门爬行纲鳄目鳄科鳄属.如图8所示，对于豺类来说，其特征表征余弦距离与同为犬科的狗类最小，其次是同为食肉目的猫，再就是哺乳纲，湾鳄也存在相同的趋势.由此从一定程度上说明模型可能生成了属于自身概念层次的embedding表征，即在同一语义空间形成了稳定的、有偏序关系的语义表征.

图8 与未出现类别的特征向量的余弦距离示意图Fig.8 Diagram of cosine distance from feature vector without category

6 总结与展望

本文提出了一种基于深度网络时不变稳定性的深度学习模型泛化能力优化方法，从数据分布角度出发，对深度学习预训练模型进行结构化分析，随后针对非稳定子结构进行选择性裁剪来实现网络剪枝，然后基于夏普比率与自注意力机制生成具有良好泛化性能的改进模型.理论分析及实验结果都表明，本方法大幅度降低了模型泛化优化过程中对于数据规模和算力的要求，同时在ImageNet 2012动物类数据集上准确率提升了6%左右，并且对数据集外部分未知动物类别的感知能力也有明显提升.我们未来计划从更多角度对特征进行组合，以更高效地提取模型有效特征，进一步降低模型复杂度同时增强模型的泛化性能，也希望本文的工作可以给后续模型改良工作者带来一些启示.