区域-道路时空图网络：一种基于图神经网络的流量预测模型

金高铭，刘 安，孙玉娥，于金刚

1(苏州大学 计算机科学与技术学院，江苏 苏州 215006)

2(苏州大学 轨道交通学院，江苏 苏州 215137)

3(中国科学院 沈阳计算技术研究所，沈阳 110168)

E-mail：anliu@suda.edu.cn

1 引 言

交通状况预测在许多城市计算系统中发挥着重要作用，如道路规划应用和交通拥堵控制系统等.但由于道路网络上的大多数交通数据(如交通流量和速度)受到复杂时空因素的影响，交通预测具有很大的挑战性.交通预测的目的是利用道路网络上观测到的历史交通数据来预测未来的交通状态.现有工作中研究的历史交通数据类型常可分为两大类：高速公路传感器数据，例如PeMS数据集[1-3]；城市交通数据，例如Taxi-NYC数据集[4-7].高速公路传感器数据通常是由数十个传感器在一段时间内的历史记录组成，包含了车流量的大小信息.而城市交通数据通常采集自电子应用程序，常见形式是出租车订单，包含了起止位置以及时间.除数据本身形式的不同，两者对地理空间的依赖上也有较大差别.高速公路的空间构成相对较简单，而且车流通常只会在高速公路网络中流动；城市区域中路网较为复杂，车流的分布较为随机.本文将主要关注城市交通数据，从而研究复杂的城市路网对交通预测的影响，而非较为简单的高速公路网.

近年来相关工作通常将交通预测建模为图问题，主要是由于路网构成了天然的非欧几里得图[3]，其中道路或路口可被视为图节点.然而，现实世界中的路网通常包含了大量的道路，导致了图的巨大化和复杂化.目前大多数研究都使用了简化的自定义图作为替代方案.例如现有工作常使用均匀网格或主干道路来将整个路网划分成多个区域[8]，并将这些区域视为图节点，从而稀疏化大规模路网.如图1左侧所示，整个城市地图被划分为多个区域，而这些区域中的每一个都会成为图中的节点，节点之间的邻接关系由这些区域在真实地理空间的相邻关系决定；图1右侧为底层复杂路网按照所属区域上色后得到的图像，其中每条道路可以视为一个节点，共同构成了一个复杂的路网图.在工作[4-7]中，历史交通数据由简化图之上的观察结果组成，受到隐马尔科夫模型的启发，本文将区域节点构成的简化图称为观测图，将道路节点构成的复杂图称为隐藏图.隐藏图中的各类隐藏状态会随着时间的流逝而变化，体现为观测图上的各种特征的不断变化.

图1 出租车区域与底层分区域后路网对比Fig.1 Taxi zones vs partitioned road network

目前大多数工作只关注上层的观测图，而忽略了下层的隐藏图.具体来说，在利用图神经网络(Graph Neural Network，GNN)捕获区域间的空间相关性时，现有的方法[4-7]通常使用基于距离的启发式规则来构建邻接矩阵，描述区域之间的邻接性.然而，对于许多交通特征(如流量或速度)而言，对区域之上的观察结果只是区域中隐藏数据的简单聚合.这意味着当两个区域在空间维度上相邻但在路网维度上相距较远时，人工构建的邻域矩阵将引入明显的噪声.

图2对观测图和隐藏图之间的关系进行了说明.上方为观测图，由a，b，c，d共4个区域构成，下方的隐藏图由代表道路的线段组成.其中深色和浅色柱状图分别代表了驶入某个区域/道路的车流量和驶出某个区域/道路的车流量.观测图中的柱状图是由下方隐藏图中对应区域的流量叠加得到.如图2中所示，区域d与c共享一条道路，同时与b共享4条道路，尽管它们在地理空间上都是相邻的，但很有可能区域b中的交通状况会对c造成更多影响.这种不同的影响在人工构造的邻接矩阵中很难被描述，导致了额外的噪声被不可避免的引入到预测过程中.此外，注意力机制[9]常常被用于描述源信息集合上的重要性分布，但由于在观测图与隐藏图之间数十倍的规模差距，现有的注意力机制很难被直接应用于描述隐藏图中节点如何影响观测图节点.

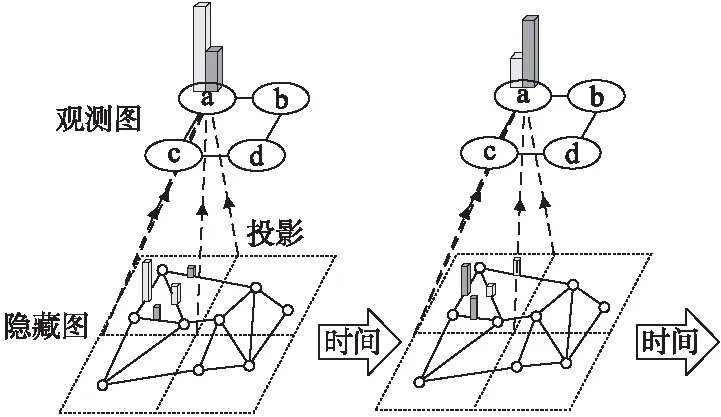
图2 观测图和隐藏图Fig.2 Observed and hidden graph

综上所述，现有工作的不足总结如下；1)现有工作通常使用自定义的区域图来建模问题，这导致了人工噪声的引入；2)由于路网的庞大和复杂，直接使用底层路网图来建模问题非常困难；3)现有的注意力机制无法很好的帮助提高预测性能.

为了解决上述问题，本文提出了一种新的模型，即区域-道路时空图网络(Region to Road Spatial-Temporal Graph Networks，R2RSTGN)，通过同时学习观测区域图和隐藏道路网络图之间的时空相关性来预测交通状况.本文的模型被设计成一个编码器-解码器结构.在编码器模块中采用压缩的多头注意机制(Compressed Multi-head Attention，CMA)来测量观测图和隐藏图之间的相关性.CMA分别考虑隐藏路网图的静态和动态特征来捕捉上下层图之间的关系.在CMA的帮助下，模型计算了输入特征和道路维度注意力的隐藏表示，并将注意力作为残差用于解码器模块.在解码器模块中，模型使用序列模型将聚集的隐图特征作为观测图的输出进行预测.

综上所述，本文中做出了以下贡献：

1)将交通预测问题的数据结构建模为观察图和隐藏图，使用细粒度的真实道路网络来提高预测性能.

2)设计了一种注意力压缩机制来学习观察图和隐藏图之间的静态和动态相关性，并提供了一个可解释的预测结果.

3)在两个真实的数据集上进行了实验.实验结果表明，对比其他同类工作，本文模型具有更优的预测性能.

本文的其余部分组织如下：第2部分介绍相关工作；第3部分定义了具有图结构的流量预测问题；第4部分介绍模型细节；第5部分给出了实验结果以及分析；第6部分总结全文.

2 相关工作

2.1 时空预测

交通预测已经被广泛研究了数十年.与早期工作中经常出现的如自回归综合移动平均法(ARIMA)和支持向量回归法(SVR)相比，基于长短期记忆神经网络(LSTM)及其变体的深度学习模型取得了令人瞩目的成就.LSTM[10]在学习时间相关性方面表现出优越的性能.ST-ResNet[11]使用基于卷积的残差网络对人群流量的周期时间特征进行建模.DeepTransport[12]使用多个LSTM层，从大而异构的数据中学习人类移动和运输模式.MDL[11]将卷积神经网络(CNN)应用于节点网络和边网络，并共同训练以理解其中的相关性.ST-3DNet[4]创新性的引入了3D卷积，可以有效地从空间和时间维度提取特征，分别使用了两个组件来建模局部时间模式和长期时间模式.

2.2 图神经网络与注意力机制

近年来，许多工作利用图卷积神经网络(Graph Convolutional Neural Networks，GCNNs)对图结构数据进行了大量的研究.ST-GCN[2]首先使用GCNNs捕获交通预测问题的非欧空间相关性.LRGCN[13]提出了一种新的路径嵌入方法，并考虑了时间相邻图之间的时间依赖性.STDN[9]在流量预测中使用周期性转移注意力来处理长期的时间转移.GMAN[3]应用注意机制来模拟历史和未来时间步之间的关系.DSAN[14]提出了多空间注意机制来过滤无关噪声.以上所有利用GCNNs对城市交通数据的研究都没有考虑到底层复杂的道路网络，而只是将地图划分为不同的区域作为节点来构造图，故无法直接应用解决本文的问题.

3 问题定义

如图1所示，本文将城市的整个路网划分为若干区域，此时可以得到两个图.

定义1.(观测图)Go=〈Vo，Eo〉，其中v∈Vo为区域，e=(u，v)∈Eo表示区域u与区域v在地理空间上相邻.显然图Go是无向图.

定义2.(隐藏图)Gh=〈Vh，Eh〉，其中v∈Vh为道路，e=(u，v)∈Eh表示道路u与道路v连通.出于简化目的，此处的联通不考虑方向性，故图Gh也是无向图.

与文献[4-7]的做法类似，本文将时间划分为时间片，并统计每个时间片上车流的信息，于是得到转移流与聚合流的定义：

定义3.(转移流)用Xtj∈|Vo|×|Vo|来表示在时间片tj中观测图Go上的输入信号.具体来说，Xtj中每个元素表示了从区域u出发且停止于区域v的车流量.

定义4.(聚合流)用Ytk∈|Vo|×2来表示在时间片tk中观测图Go上的观测信号.具体来说，表示了在此时间片内所有从区域v出发的流量；表示了在此时间片内所有到达区域v的流量.

利用上述定义，可以将交通预测的问题描述为：

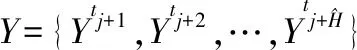
4 解决方案

4.1 框架总述

R2RSTGN的架框架图3所示.首先，模型通过编码器模块学习从观察信号到隐藏状态的映射函数.编码器模块采用压缩多头注意力(CMA)来同时考虑静态道路嵌入与动态时间嵌入.然后，本文使用了带残差的注意力机制来捕获和传递复杂的时空相关性，最后使用GCN来聚合最终输出.

图3 模型框架Fig.3 Architecture of R2RSTGN

4.2 带压缩注意力机制的编码器

由于交通工具的运行被限制在实际的交通网络之上(如汽车专用道和自行车专用道)，区域间的交通流量很大程度实际上是由路网本身的结构决定的.所以一种非常自然的想法是利用注意力机制来描述交通流量对道路的倾向性.然而，区域网络与道路网络之间数十倍以上的体量差距，使得在两者间共享的注意力机制的训练低效且困难.

为了解决这个问题，本文提出了压缩的多头注意力机制CMA.在CMA中，模型使用了图卷积神经网络来提取区域网络以及道路网络的空间特征.

给定一个无向图G，其对称规范化拉普拉斯矩阵由Lsys=D-1/2LD-1/2∈R|V|×|V|，L=D-A给出，其中D，A，V分别是图G的对角度矩阵，邻接矩阵和顶点集.一个基本的图卷积运算表示如下：

其中U∈R|V|×|V|是Lsys的特征向量矩阵，∧是Lsys的特征值的对角矩阵，Θ(∧)是可学习的卷积核，x，y是输入输出图信号.出于精度和效率方面的考虑[15]，本文在具体实现过程中使用Cheby-Net变体.记图G和信号X之间的GCN操作为G⊗x.

道路嵌入R∈R|Vh|×Rh表示了道路在路网图结构中所拥有的空间信息，是模型学习的目标之一，其初始值由随机初始化得到，并在每轮训练之后更新.

R′=Gh⊗R

(1)

(2)

其中vo∈Vo表示观测图中某一个区域节点，T表示矩阵的转置，Mv∈R|Vh|为遮罩矩阵用于过滤掉无效信息，只保留对应的区域信息，定义为：

(3)

需要说明的是，对于所有区域，R′在一轮训练过程中只需要被计算一次，原因是静态道路特征不应该随时间变化.

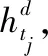
(4)

其中σ是非线性激活函数，‖是广播拼接操作.

接下来，对于一个在时间片tj中的观测区域vo，可以通过对所有的动态道路隐状态采用K并行多头注意力机制来得到一个带权和，以作为其空间隐含表示svo，tj：

(5)

(6)

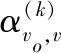
注意力得分由区域的隐藏状态和动态道路隐藏状态使用softmax计算：

(7)

其中相关性函数score采用了[9]的做法，利用缩放点积来计算：

(8)

4.3 道路级注意力机制

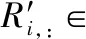
(9)

(10)

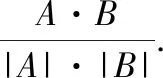
(11)

接下来利用道路维度注意力可以计算残差，用于给后续的解码器模块传递无损的原始信息.不同于传统的直接拼接残差，从原始输入中挑选更加重要的部分可以减少引入的误差.具体来说，本文使用了一个阈值Q来过滤了那些不重要的路段信息，并将剩余部分组成了残差residualvo，tj∈R|Vo|×Rh：

(12)

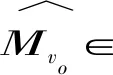
(13)

有关阈值Q的选取会在实验部分讨论.

4.4 解码器

基于上述CMA模块，模型通过捕捉空间特征得到空间表.接下来，通过使用带有道路注意力的顺序模型来捕获时域中的相关性.

由CMA得到空间表示s=sv1，sv1，…，sv|Vo|，其中svo，tj∈svo是区域vo在时间片tj上的空间表示.在这里，首先应用门控循环单元(Gated Recurrent Unit，GRU)[16]，定义如下：

(14)

zvo，tj=σ(Wzsvo，tj+Uzhvo，tj-1)

(15)

(16)

rvo，tj=σ(Wrsvo，tj+Urhvo，tj-1)

(17)

(18)

(19)

5 实 验

5.1 数据集

本文在两个大规模公开真实数据集上评估模型：

· Taxi-NYC来自出租车数据平台NYC-TLC(1)https：//www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page.使用的是从2019年3月1日～2019年4月31日之间位于纽约市曼哈顿的出租车订单记录.记录中包含订单起始时间和订单起始地点.前40天作为训练数据，其余20天作为测试数据.Taxi-NYC还提供了如图1所示的出租车区域地理信息文件，其中包含69个出租车区域及其边界信息.

· Bike-NYC来自纽约出租车共享系统citibike(2)https：//www.citibikenyc.com/system-data获得.使用的是从2019-03-01～2019-04-31年间在纽约市曼哈顿收集的记录.记录上有起止时间和起止地点.前40天作为训练数据，其余20天作为测试数据.

· 使用来自纽约市曼哈顿的OpenStreetMap(OSM)(3)https：//www.openstreetmap.org的地图数据.原始地图数据包含9884条道路.

5.2 预处理

首先检查了出租车区域的邻接性，并选择了其中的64个，因为其他5个区域在地理空间上没有任何一个区域与其相邻.然后根据与这些区域的所属关系从所有道路中保留了8141条道路，并划分为64组，如图1左侧所示.最后，将NY-TaxiC和NYC-Bike中的所有出行记录按照区域图和时间间隔聚合为2880行64×64列的转移流数据和2880行64列的聚合流数据.需要注意的是，OSM的原始道路图是一个有4579个十字路口作为顶点和9884个道路作为边的图.但由于本文重点关注的是道路特征，因此将原始图中的边(即道路)构建为顶点，将顶点(即十字路口)构建为边，将原始图转换为新的线状图[17].转换方法的研究已经比较成熟了，故本文省略了转换的细节.

5.3 实验参数设置讨论

遵循已有的相关工作[14]，本文选取12作为输入和输出观测序列的长度，选取6小时作为时间片的大小.在训练过程中采用Adam优化器[15]，初始学习率为0.001.

如数据预处理部分介绍的，观测图顶点数为|Vo|=64，隐藏图顶点数为|Vh|=8141.使用Rh=128作为道路隐向量的嵌入长度，注意力头数量为K=4.

本文用以下基线方法评价R2RSTGN：1)自回归综合移动平均(Auto-Regressive Integrated Moving Average，ARIMA)；2)支持向量回归(Support Vector Regression，SVR)；3)前馈长短期记忆网络(FC-LSTM)是一种采用全连接LSTM层的编译码模型，曾在序列预测方面取得了突破进展；4)时空图卷积网络(Spatio-Temporal Graph Convolutional Network，STGCN)[2]采用了带有卷积操作的卷积序列学习层；5)图多注意网络(Graph Multi-Attention Network，GMAN)[3]在编解码器结构中应用图多注意网络；6)动态选择注意力网络(Dynamic Switch-Attention Network，DSAN)使用了多空间矩阵分解.对于ARIMA、SVR和FC-LSTM，本文使用了工作[7]中介绍的相同设置.对于模型STGCN、GMAN和DSAN，分别使用对应原文建议的默认设置.

5.4 实验结果

对表1给出了模型在未来30分钟(1步)、3小时(6步)、6小时(12步)中在Taxi-NYC和Bike-NYC数据集聚合流的预测结果.使用均方根误差(Root Mean Squared Error RMSE)作为评价指标.从表中可以看到，深度学习方法比传统的时间序列方法(ARIMA、SVR)表现得更好，因为传统方法完全忽略了空间和其他复杂的上下文特征.

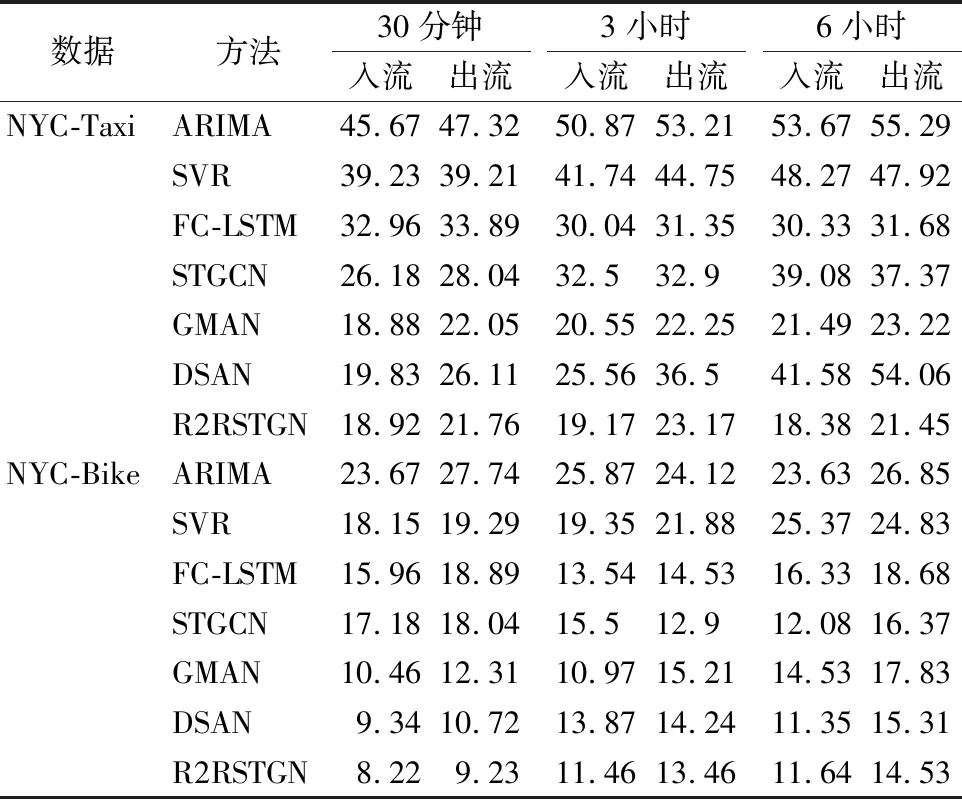
表1 不同方法间的预测性能对比Table 1 Prediction performance comparison of different approaches

FC-LSTM使用了长短期记忆网络，相比传统模型能在时间维度上捕捉更多的相关性；STGCN创新性地将图卷积应用于交通预测问题，但是缺少过滤机制的残差传递过程使其易受数据中噪声影响.具有复杂架构的模型(GMAN、DSAN、R2RSTGN)在STGCN的基础上加入了注意力机制来学习空间和时间特征之间的综合关系，明显优于其他模型.本文提出的R2RSTGN比所有对比模型取得了更好的预测性能，在两个数据集上都取得了最低的RMSE.

5.5 有效性分析

本节研究了CMA模块在R2RSTGN模型中的有效性.R2RSTGN列表的一些变体如下：

1)R2R-FNN：在这种变体中，整个CMA模块被两个简单的前馈网络所取代.第1个参数为w∈(Rh+Th)×|Vo|的网络将道路嵌入和时间嵌入的连接映射为动态嵌入.第2个参数W∈2|Vo|×|Vo|的网络将输入X和动态道路嵌入的连接映射到后续隐藏嵌入.

2)R2R-NGCN：这个变体的区别是所有CMA中的GCN操作都被去除.

3)R2R-NR：在这个变体中从CMA中计算得到的道路注意力不会通过残差进入后续的解码器.

上述几个变体的表现如图4与图5所示.R2R-FNN由于使用了简单的全连接层来替代CMA，导致完全忽视了路网的空间结构，在所有变体中表现最差.其次较差的是R2R-NGCN，证明了图卷积运算对于提取空间特征是必不可少的.R2R-NR的性能比R2RSTGN稍差，主要是由于缺少了带过滤的残差机制.

图4 不同变体的预测性能对比Fig.4 Variants performance comparision

5.6 道路注意力分析

道路的注意力得分可以显示某个时间片上道路的重要性，选取了2019年4月3日中3个时间段上模型输出的注意力得分进行了可视化，如图5所示.

图中的注意力值归一化到[0，1]之间，表示当前时间片上每条道路对整个观测的相对重要性.图中颜色越深代表其道路获得注意力值越高.可以观察到图5(a)中的道路整体颜色比图5(c)的要深，虽然图5(a)对应的是午夜时间，应该是比较空旷的.一个重要的原因是颜色深浅表明了相对的重要性，而不是交通热度；在午夜道路整体更加空旷，导致了许多路段的之间的差异性减少从而体现的同样重要.另一方面，图5(c)的注意力图在高峰时段的颜色更加不均匀的，显示少量路段具有较高的重要性，一个合理的推断是当时很少有关键道路对整个地图上的观察有显著的影响.这些数据为模型预测提供了可解释性，有助于路线规划等问题的解决.

图5 不同时段的道路注意力可视化Fig.5 Roads attention visualization at different times

5.7 模型参数探讨

在接下来的实验中，本文研究了超参数对模型的影响.首先，对控制道路嵌入生成残差的阈值Q进行实验.图6(a)给出了Taxi-NYC和Bike-NYC的1步(30分钟)预测的RMSE.可以观察到，RMSE都随着阈值的增加而减少，并且在阈值增加到1之前达到了最小值.当RMSE达到Taxi-NYC和Bike-NYC的最小值时，阈值Q约为0.7和0.6.可以得到以下几个推论：1)在阈值设置为0时，残差部分退化为最简单的连接残差，阈值设置为1时，残差完全消失，而采用一个适当的过滤阈值能有效提高模型预测的精度，说明原始数据中携带了较多噪声，不适合不加区分的生成残差；2)出租车模型中最优阈值的选取相比自行车模型更高，这是因为驾驶路网有更高的拥堵发生率，所以每条道路的重要性更不均衡.实际上，阈值可以看作是一种噪声滤波器，模型用它来去除低频噪声，提取路网的重要特征.本文还对道路嵌入的隐藏状态大小进行了实验，结果如图6(b)所示，道路嵌入的高维数对预测更有效.随着隐藏维度的增大，精度提高逐步减少但模型训练时间快速增加，因此本文使用H=150作为隐藏维度的大小.

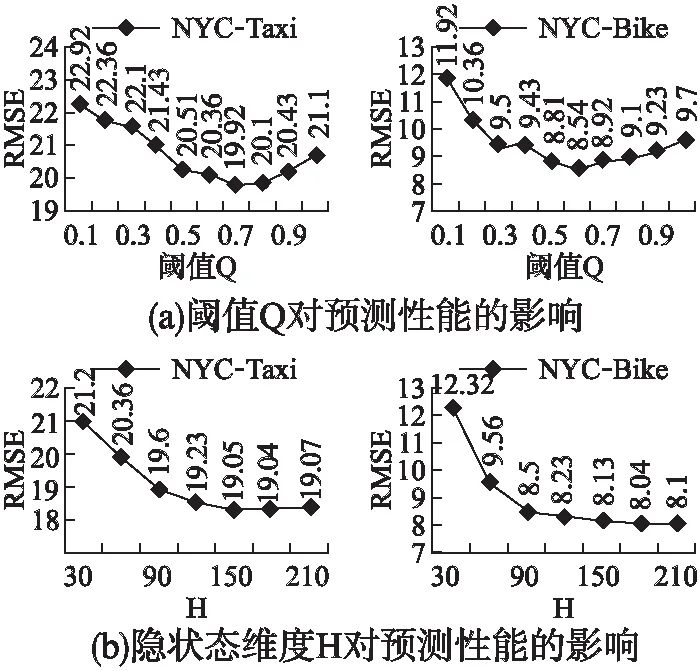
图6 参数Q、H对预测性能的影响Fig.6 Performances by Q and H

6 结论以及未来工作

本文通过将空间数据结构建模为观察图和隐藏图，研究了流量预测问题，并提出了一种新颖的区域-道路时空图网络模型R2RSTGN来解决此问题.为了捕捉两个图之间的相互作用，模型使用一个具有图卷积运算的压缩注意力模块来提取空间特征.同时，利用阈值结合道路维度注意力来滤除原始输入数据中的噪声从而产生残差，并将残差连接到序列解码器以提高模型预测精度.在两个真实数据集上的大量实验证明了R2RSTGN的性能.

下一步的工作包括探索更有效的方法来增强道路嵌入表示和预测性能.另外，更复杂的图网络变体也值得研究.