一种参数动态更新的布谷鸟搜索算法

闫 河，谢 敏，赵其峰，李晓玲

1(重庆理工大学 两江人工智能学院，重庆 401135)

2(重庆理工大学 计算机科学与工程学院，重庆 400054)

E-mail：cqxiemin@gmail.com

1 引 言

在自然界中，布谷鸟[1]会将卵产在宿主鸟巢里，布谷鸟幼鸟会本能地模仿宿主幼鸟行为来降低被宿主鸟发现的概率[2]，当幼鸟被发现时，布谷鸟需重新寻找鸟巢产卵.大量实验表明，布谷鸟寻找宿主鸟巢的飞行行为属于随机游走，飞行步长满足Lévy分布[3]，是生物界中常见的动物觅食飞行方式[4].布谷鸟搜索(Cuckoo Search，CS)算法就是依据布谷鸟“寄巢产卵”行为提出的模型[5]，其主要思想是利用Lévy飞行策略产生候选解，并利用贪婪策略更新解，在一定概率下舍弃部分解后，通过偏好随机游走策略产生新解替换淘汰解，通过不断迭代最终使得解达到全局最优.

CS算法作为一种典型的群智能优化算法，具有参数少，结构简单，易于实现等优点[6]，在各领域均得到了广泛的应用[7，8].但是固定的步长缩放因子使得算法容易陷入局部最优[9]，且偏好随机游走策略是通过任意选择当前鸟巢解来生成新解，具有随机性[10]，因此有学者对存在的问题进行了改进.孙敏等人[11]将混沌扰动策略引入CS算法(Chaotic Cuckoo Search Algorithm，CCSA)，通过Circle映射有效的防止了算法陷入局部最优，文献[12]提出了一种基于贝塔分布的CS算法(Cuckoo Search Algorithm with Beta Distribution，BCS)，采用贝塔分布随机数设置Lévy飞行步长，增强了算法收敛速度；文献[13]针对高维优化存在维间干扰现象，提出了基于逐维改进的CS算法(Cuckoo Search Algorithm with Dimension by Dimension Improvement，DDICS)，将各维度最优解组合成新解，有效地改善了解的质量；文献[14]利用教与学搜索策略(Teaching-Learning-Based Optimization，TLBO)提高算法局部搜索能力，采用精英解方法强化优势信息学习，引入模拟退火机制避免算法陷入局部最优，面对复杂多目标图像分割具有一定优势，本文将文献[14]提出方法暂命名为TLBOCS算法.

虽然改进的布谷鸟算法都在不同程度上提升了算法性能，但寻优的准确性依然较低.因此，本文提出了一种参数动态更新的布谷鸟搜索算法.首先，利用柯西分布随机数生成Lévy飞行步长，记录每代最优解对应均值参数，以此生成下一次迭代所需的新的柯西分布[15，16]，这种步长更新策略能够充分利用迭代信息，使得局部搜索更加灵活；其次，提出正态干扰策略生成干扰解，同时保留每代最优解对应的均值参数，以此生成下一次迭代所需的新的正态分布[15，17]，完成正态干扰参数的更新；再利用模拟退火算法(Simulated Annealing，SA)[18]的Metropolis准则在新解和干扰解中择优，该方法使得算法具有容差性，在一定概率下保留适应度较低的解，避免陷入局部最优；最后，利用轮盘赌选择[19]和双向随机搜索策略强化优势解的学习，生成新解来替换被淘汰的解.实验结果表明，本文提出方法具有较高的准确性和稳定性.

2 基于参数动态更新的CS算法

2.1 基于柯西分布的Lévy飞行策略

在经典CS算法中，步长缩放因子是固定的，易陷入局部最优[10]，步长大，损害搜索精度，步长小，降低搜索速度.文献[12]采用Beta分布设置步长缩放因子，虽然提高了算法性能，但容易陷入局部最优，且随着维度增加，算法性能有所下降.针对该问题，本文采用柯西随机数进行更新，更新公式如下：

Xg+1=Xg+Cauchy⊗Levy(β)

(1)

(2)

(3)

Cauchyi=randci(μCauchy，0.1)

(4)

μCauchy=(1-d)·μCauchy+d·meanL(SCauchy)

(5)

(6)

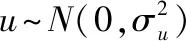
2.2 基于正态扰动和模拟退火的更新策略

为了避免算法陷入局部最优，引入SA算法的Metropolis准则，在一定概率上保留适应度较差的解可以有效避免算法陷入局部最优.Metropolis准则评价的两组解为2.1节生成的新解以及采用正态随机数生成的干扰解.解的评价准则以及干扰解生成方法如下：

exp(F(XNormal)-F(Xg))/Tg)>rand

(7)

XNormal=Normal⊗Xg

(8)

Normali=randni(μNormal，0.1)

(9)

μNormal=(1-d)·μNormal+d·meanA(SNormal)

(10)

Tg+1=kTg

(11)

其中，式(7)为Metropolis准则，F(·)为适应度函数，Tg为当前退火温度，设定初始温度T0=F(Xpbest)/ln(5)，Xpbest为当代最优解，rand为(0，1)随机数，XNormal为自适应正态随机数生成的新解，Normali为第i个正态随机数，Normal=(Normal1，…，NormalN)，randni(·)为正态分布，μNormal为正态分布均值，meanA为标准的算术均值，k为降温衰减系数，SNormal与SCauchy一样，均为成功参数集合.正态随机数的生成方式与2.1节柯西随机数生成方式相似，利用每代最优解对应的正态分布均值生成新的正态分布，并以此生成下一代新解所需参数.

2.3 基于轮盘赌和双向随机搜索策略

自然界中，当卵被宿主发现时，布谷鸟需要重新寻找鸟巢产卵，而寻找新巢的方式是随机的.基本CS算法中，是根据偏好随机游走策略生成新解来替换被淘汰的解，这种策略采用双随机解来更新随机游走步长，没有充分利用优势解的信息，且随机游走搜索方向由(0，1)区间的随机数决定，这种单向搜索在一定程度上限制了搜索的随机性[13].轮盘赌方法是遗传算法中使用最多的选择策略之一，其基本思想是每个解被选中的概率与其适应度大小成正比，本文利用轮盘赌选择适应度较好的优势解替代随机解，并增加解的反向搜索能力，在保证算法朝着全局最优解迭代的同时，也保留了解的多样性.偏好随机游走公式如下：

Xg+1=Xg+φ⊗Heaviside(Pa-ε)⊗(Xi-Xp)

(12)

其中，Heaviside()为单位阶跃函数，φ为(-1，1)区间内的随机方向系数，使得算法具有双向搜索能力[13]，Pa为解被淘汰的概率，ε为(0，1)区间内的随机数，Xi为当代随机解，Xp为轮盘赌选出的解.

2.4 改进算法的流程

算法流程抽象如下.其中，逐维更新解策略采用的是文献[13]的方法，pbestFit为当前迭代最优适应度，Xpbest为每次迭代的最优解集，gbestFit为全局最优适应度，Xgbest为全局最优解，Xa，i为Lévy飞行生成的第i个新解，Xnew，i为需进行逐维比较的第i个解，Xnew，(i，j)为Xnew，i的第j维解，Xa，(i，j)为Xa，i的第j维数据，Xnew，i其他维度的解为第g代对应维度解，Xg，i为第g代的解集第i个解，Xpbest，i为第g代最优解集的第i个解.

算法1.改进布谷鸟算法

begin

初始化种群大小N和解：Xi，(i=1，2，…，N)；

计算解的适应度F(Xi)，保留最优适应度pbestFit，对应解Xpbest；

设置初始温度T0；

设置柯西分布μCauchy与正态分布μNormal的初始均值；

while(未达到最大迭代数)

fori=1 to N

生成柯西随机数Cauchyi；

利用公式(1)-公式(6)生成新解Xa，i；

Xnew，i=Xg；

// 逐维更新解

forj=1 toD

Xnew，(i，j)=Xa，(i，j)；

ifF(Xnew，(i，j))>F(Xg)//适应度比较

Xg=Xnew，(i，j)；//单维度更新

end

//当前解优于全局解，跳出逐维更新循环

ifF(Xnew，(i，j))>F(Xgbest)

break；

end

end

end

更新当代解的适应度F(Xg)；

fori=1 to N

生成正态分布随机数Normali；

利用公式(8)生成干扰解XNormal，i；

end

根据Metropolis准则在新解和干扰解中择优；

退温操作，Tg+1=kTg；

fori=1 toN

ifr>Pa

利用轮盘赌选出Xp，按照式(12)生成新解代替Xg，i；

end

end

//更新当代最优解，并记录对应参数

fori=1 toN

ifF(Xg，i)>F(Xpbest，i)

Xpbest，i=Xg，i；

pbestFit_i=F(Xg，i)；

记录SCauchy和SNormal；

end

end

利用公式(5)和公式(10)更新μCauchy和μNormal；

保留全局最优解Xgbest以及适应度gbestFit；

end

输出全局最优解；end

3 改进算法性能测试实验与分析

3.1 基本测试函数实验与分析

为了测试改进算法性能，选取了6个优化算法常用的测试函数进行试验[20，21]，如表1所示，6个测试函数最优值均为0.表2为各算法参数配置.

表1 测试函数Table 1 Test functions

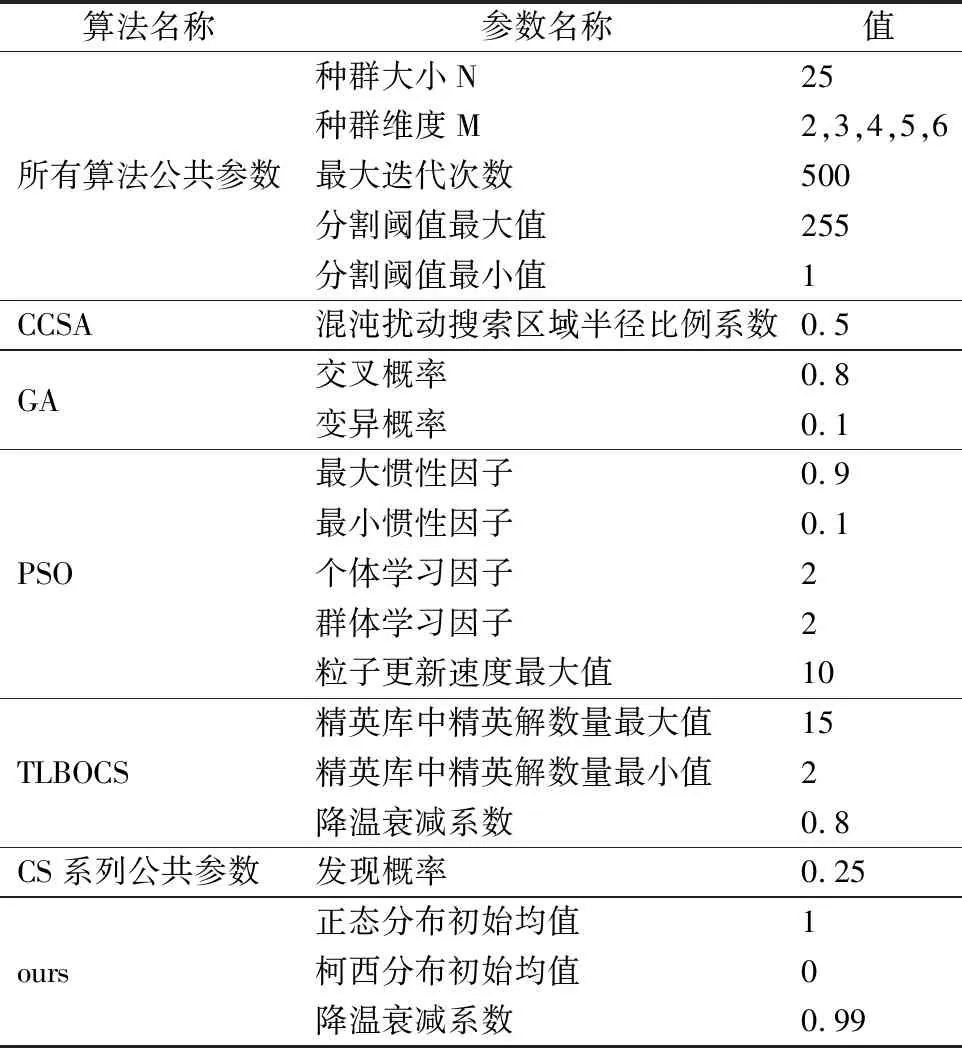
表2 各算法参数Table 2 Parameters of each algorithm

表3为本文改进算法与粒子群算法(Particle Swarm Optimization，PSO)[22]、遗传算法(Genetic Algorithm，GA)[23]、经典CS算法、BCS、DDICS等7个算法在6个基本测试函数上的运行结果，图1为对应适应度曲线图.算法各执行20次，单个迭代次数为500，由于篇幅限制，表3只显示种群维度为6时各算法的平均适应度值，图1也是6维的适应度曲线图.

从表3可以看出，本文算法能够较稳定的迭代到最优解，算法稳定的原因主要有：

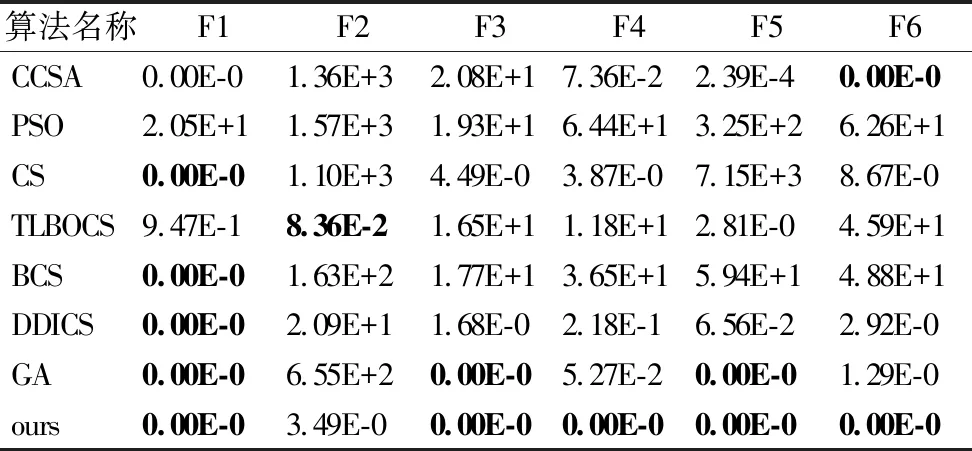
表3 各算法平均适应度Table 3 Average fitness of each algorithm

1)Lévy飞行步长的更新以及逐维求解策略，使得算法搜索在不受维间干扰的同时，能够始终向着全局最优解迭代；

2)利用正态随机数生成干扰解，加上模拟退火机制使得算法具有容差能力，保证解的丰富性，避免陷入局部最优；

3)充分利用优势解信息，通过轮盘赌方法选择适应度较优的解来辅助生成新解，完成替换.

从图1可以看出，本文提出算法能够较快的收敛到全局最优，虽然在图1(b)中比TLBOCS和CCSA算法效果差一点，但是从其他图来看，TLBOCS算法具有一定的不稳定性，而CCSA算法在其他基本函数上的结果比本文算法差了一点.使用柯西随机数更新Lévy飞行步长，收集每代最优解的柯西分布均值，利用这些参数构建新的柯西概率分布，使得步长能够根据迭代情况更新，这也是本文算法能够稳定迭代到全局最优解的关键.

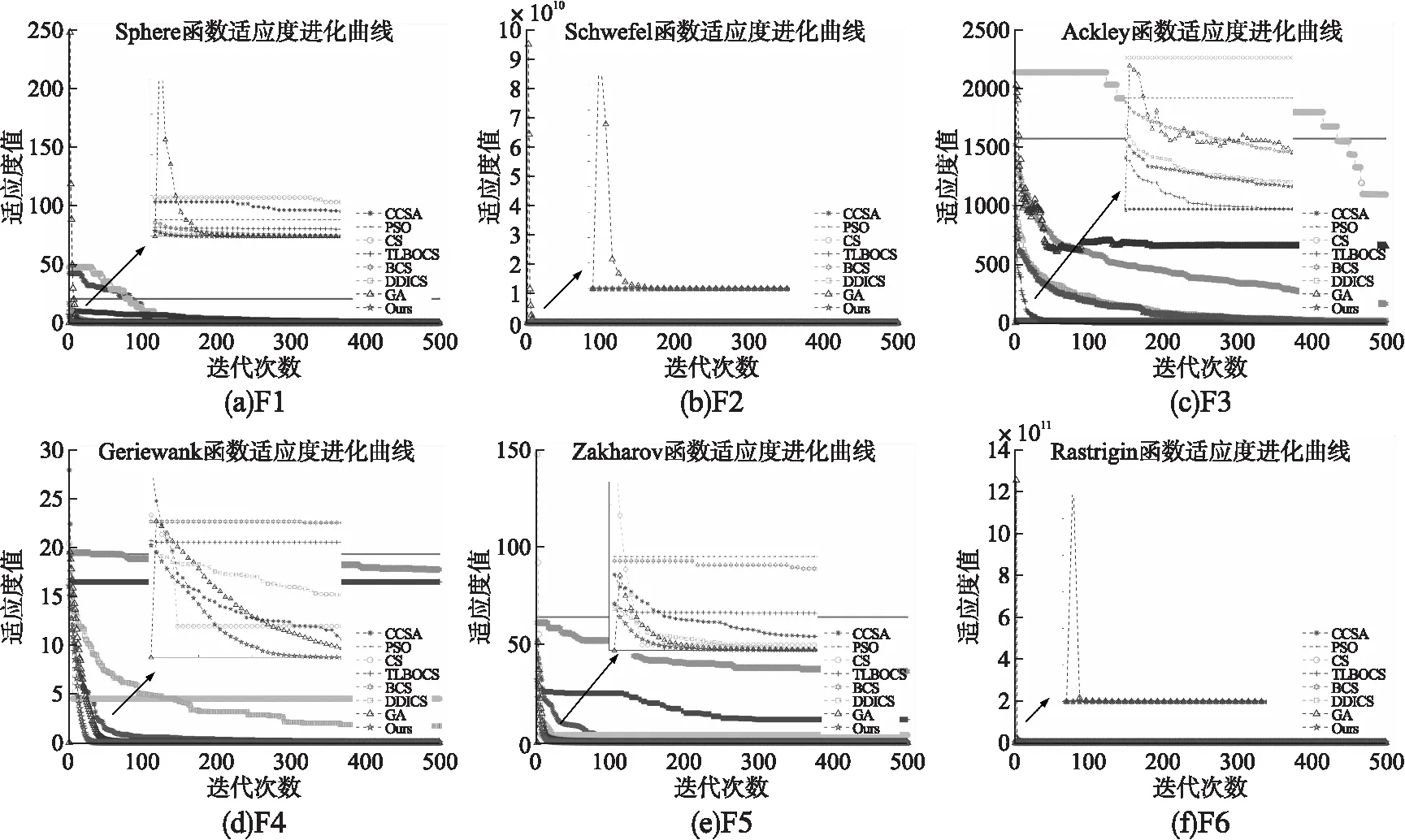
图1 测试函数的适应度曲线Fig.1 Fitness curves of test functions

3.2 多阈值图像分割实验与分析

为验证本文算法优化能力，采用文献[24]的多阈值Otsu分割函数作为适应度函数，并选择一张经典的Lena图像以及伯克利大学图像分割库中的一张图像进行试验.试验环境为Ubuntu 18.04系统，3.6GHz和32GB内存微处理器，运行软件为MatlabR2018a.

本文除了与上节7个算法进行对比，还增加了去除2.1-2.3节改进方法的3组对比实验，分别命名为Ours1，Ours2和Ours3.

图2和图3为算法各执行20次得到的结果，从图2可以看出，本文改进方法分割效果优于大部分对比算法，在一些细节上和原图更为接近，说明本文提出的方法能够较好的分割图像，图2(i)～图2(k)对比CS等算法也体现出了优势，但是在背景细节上处理得比图2(l)差一点，说明本文提出的3个改进点对于算法性能均有提升.图3(a)是目标更为复杂的伯克利图像，在处理衣服和裤子这种颜色比较接近的目标时，其他算法如CA等将这两部分视为同一目标进行分割，而本算法依然能够较为完整的分割，说明本文提出算法更加高效，能够成功分割不同图像.

图2 Lena的阈值分割结果图Fig.2 Lena figure of threshold segmentation

图3 伯克利图像的阈值分割结果图Fig.3 Berkeley figure of threshold segmentation

图4和图5为各算法执行1次得到的适应度进化曲线，从两图中可以看出，本文能够较快的完成收敛，自适应步长使得算法局部搜索能力更加灵活；正态扰动和模拟退火避免了算法陷入局部最优，而经典CS算法在早期迭代时就陷入了局部最优.去除改进步骤的3个结果也优于部分对比实验，验证了算法改进的有效性.

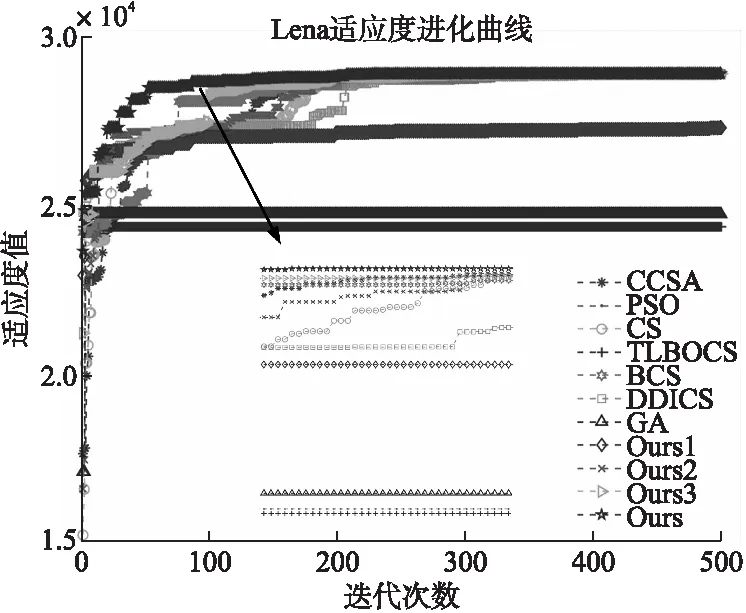
图4 Lena的分割结果适应度曲线Fig.4 Fitness curves of Lena′s segmentation images

图5 伯克利图像分割结果适应度曲线Fig.5 Fitness curves of Berkeley′s segmentation images

为了更直观的评价图像分割效果，本文选用峰值信噪比(Peak Signal to Noise Ratio，PSNR)[9]和结构相似性(Structural Similarity，SSIM)[9]来进行量化评价.峰值信噪比计算公式如下：

PSNR=10log(255/MSE)

(13)

(14)

结构相似性计算公式如下：

(15)

表4为各算法分割结果性能指标，可以看出，本文算法在低维时和其他布谷鸟类算法几乎没有差距，随着维度的增加，PSNR和SSIM的差距也越明显，DDICS在5维的时候虽然比较高，但是在6维的时候算法性能降低.非布谷鸟类算法在低维空间处理时具有一定的优越性，但是部分算法在高维空间具有不稳定性，如PSO算法在6维空间时PSNR与SSIM均有明显的下降.本文算法对比GA算法部分效果虽然要差一点，但是GA算法在5维空间上处理时，PSNR有所下降，SSIM算法在6维空间处理时也比不如5维空间的结果，而本文算法效果在维度上升的同时，保持了本身的稳定性，逐步优化，验证了本文算法的有效性.本文改进算法在去除部分步骤后的性能有所下降，体现了改进部分的重要性.

表4 各算法性能指标Table 4 Performance indexes of each algorithm

续表

4 结 论

为提升布谷鸟算法在高维空间的搜索能力与稳定性，提出了一种参数动态更新的布谷鸟搜索算法，随着维度的增加，算法性能能够稳步提升.该算法提出的步长更新策略能够充分利用迭代信息，使得局部搜索更加灵活，正态随机干扰保证了解的多样性，Metropolis准则使得算法具有容差性，避免算法陷入局部最优，轮盘赌选择和双向随机搜索方法充分利用优势解信息完成新旧解的替换.通过与PSO、CS、DDICS等算法进行对比，发现本文算法搜索能力和稳定性的结果更好.虽然改进算法拥有较高的准确性，但是因在原有算法基础上增加了模拟退火机制，使得算法增加了择优判断步骤，时间复杂度随之提高，未来将继续深入研究各种启发式算法，使得改进算法能够在保证分割准确的同时，保证分割效率.