尾斜浪中纯稳性丧失直接评估方法研究
2022-08-20祁江涛
祁江涛 鲁 江
(1.中国船舶科学研究中心 水动力学重点实验室 无锡 214082; 2深海技术科学太湖实验室 无锡 214082)
0 引 言
2020年12月10日国际海事组织(IMO)海事安全委员会(MSC)102届会议批准了第二代完整稳性衡准暂行指南,该衡准体系由5种稳性失效模式、3层评估方法以及航行作业指南/操作限制构成。受全球新冠肺炎疫情的影响,直到2022年4月国际海事组织海事安全委员会105届会议批准了二代稳性暂行指南的解释性文件。历经10年的努力,二代稳性终于变成船舶界的海事法规。纯稳性丧失是二代稳性衡准5种稳性失效模式之一。
纯稳性丧失被认为是船舶波浪中丧失静稳性导致的静态倾覆模式。波浪中稳性与静水中的稳性有很大的不同,船舯位于波谷时横摇复原力变大,船舯位于波峰时横摇复原力变小。在旧金山湾天然风浪中进行的大尺度船模试验中,随浪中,船舯位于波峰时,船模会突然失去稳性并发生倾覆,纯稳性丧失被定义为一种新的稳性失效模式。这个阶段,国内外许多学者的研究重点在于规则波和不规则波中横摇复原力计算方法,典型代表如KUO 等以及HAMAMOTO等。UMEDA 等为研究复原力变化对参数横摇影响,在复原力计算中采用切片理论计算的时域垂荡、纵摇替代静平衡法中的升沉和纵倾。鲁江等为研究随浪/尾斜浪中纯稳性丧失,进一步拓展这个方法,采用时变垂荡、纵摇的振幅和相位计算波浪中横摇复原力变化。
纯稳性丧失被认为是波峰处复原力丧失和停留时间导致大幅横摇失稳的倾覆模式。除非波浪中横倾角过大或稳性高变成负值,在没有外界横倾力矩时,当波峰经过船舶后,船舶最终会回到正浮状态。BASSLER 等认为制定纯稳性丧失衡准的难点在于纯稳性丧失不局限于波浪中复原力计算。NEVES综述了纯稳性丧失预报方法。HASHIMOTO通过比较随浪中横摇单自由度数学模型、纵荡-横摇耦合的二自由度数学模型和试验结果,确认波峰处复原力丧失和停留时间是导致大幅横摇失稳的原因。鲁江等构建了纵荡-横摇二自由度运动耦合的数学模型,进行了随浪中纯稳性丧失直接评估;之后,进一步构建了随浪中纯稳性丧失新的纵荡-垂荡-横摇-纵摇耦合的四自由度数学模型,同试验结果进行了比较,并指出随浪中不考虑固定横倾力矩时数值计算和试验不能重现纯稳性丧失现象。这个阶段,学者研究重点是时域模拟纯稳性丧失现象。
尾斜浪纯稳丧失被认为不是“纯”的稳性丧失。UMEDA首先指出尾斜浪纯稳性丧失不是“纯”的稳性丧失,操纵运动中的横荡、艏摇产生的离心力形成的横倾力矩是尾斜浪中船舶倾覆的1个重要原因,而后又进一步确认1艘实船尾斜浪中由于操纵运动中的横荡、艏摇产生的离心力导致倾覆。IMO衡准制定过程中,日本代表指出他们新构建的纵荡-横荡-横摇-艏摇耦合的四自由数学模型比纵荡-横摇耦合的二自由度数学模型能更好地预报纯稳性丧失,IMO二代稳性工作组同意采用纵荡-横荡-横摇-艏摇耦合的四自由度数学模型预报纯稳性丧失。针对IMO直接稳性评估的要求,鲁江等初步构建了纵荡-横荡-横摇-艏摇四自由度运动耦合的数学模型;之后,基于标准MMG操纵性方程,构建了一套满足IMO直接评估要求的纯稳性丧失标准数学模型,并对其中的参数表达式进行了标准化;进一步构建了纵荡-横荡-垂荡-横摇-纵摇-艏摇耦合的 六自由度数学模型,研究了尾斜浪纯稳性丧失。
针对二代稳性衡准在船舶界的应用,不规则波中纯稳性丧失直接评估软件列入国产CAE软件开发模块之一。纯稳性丧失现象表现为失稳大幅横摇运动,甚至倾覆,涉及到失稳运动中船体瞬时湿表面的自由波面强非线性模拟技术,同参数横摇数值方法有重叠部分。纯稳性丧失现象发生在随浪和尾斜浪中较高航速的船舶,和骑浪/横甩现象存在速度重叠区域,力学模型和骑浪/横甩有重叠部分。有必要构建纯稳性丧失精细化时域力学模型,实现纯稳性丧失、骑浪/横甩和参数横摇在统一预报力学数学模型。2021年10月11日,中国船舶科学研究中心发布了二代稳性评估软件HydroSTAB。本文采用HydroSTAB的扩展版,开展了尾斜浪中纯稳性丧失直接评估方法研究。该方法在参照标准操纵性MMG方程、双桨双舵MMG方程、骑浪/横甩数学模型和参数横摇预报方法基础上,构建纵荡-横荡-垂荡-横摇-纵摇-艏摇六自由度耦合的非线性时域运动数学模型,其中F-K力和静水力采用了参数横摇的瞬时湿表面积分方法。
1 数学模型
1.1 船舶运动坐标系
空间固定坐标系-,原点位于水平面,轴向下为正,该坐标系用来描述波浪。波浪沿轴正向传播,初始时刻波谷位于原点;船体坐标系-,以船舶重心为原点,该坐标系随船一起摇荡;参考坐标系-,和船体坐标系原点重合,但不随船舶横摇、纵摇和艏摇。采用平均湿表面积分时,船体型值在参考坐标系和船体坐标系下一致。

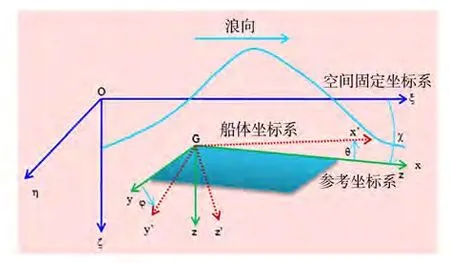
图1 坐标系
1.2 数学模型构建
本文构建了纵荡-横荡-垂荡-横摇-纵摇-艏摇六自由度数学模型进行纯稳性丧失运动数值预报。纵荡、横荡、横摇、艏摇运动方程参照文献和文献,如公式(1)至公式(4)所示。垂荡、纵摇运动方程如公式(5)和公式(6)所示。


采用文献[32]的加强积分法计算速度势,以库文件形式先计算出不同航速下的垂荡、纵摇运动的振幅和相位,然后根据实时航速,插值得出实时航速下的垂荡、纵摇振幅和相位,代入到公式(7)和(8)中,求出时域垂荡、纵摇运动。从公式(9)可以看出,实时船-波相对位置考虑了纵向速度、横荡速度和艏摇角,即垂荡、纵摇时域运动耦合了纵荡、横荡和艏摇的影响。纵荡、横荡、横摇和艏摇方向的F-K力和静水力采用瞬时湿表面积分技术,而时域绕射力和辐射力(附加质量和阻尼系数)采用平均湿表面积分,但考虑了瞬时速度影响,原理和时域垂荡、纵摇运动类似。

式中:下标,分别为船体力和舵力,公式(5)和(6)是传统的耐波性方程。
ζ()为时域垂荡运动;()为时域纵摇运动;ζ()为航速时的垂荡运动振幅,m;δ()为对应的初始相位,rad;θ()为航速时的纵摇运动振幅,m;δ()为对应的初始相位,rad;ξ/为船舶和波浪的相对位置;χ为目标航向;为考虑艏摇运动()的实时航向;C为波速,m/s。
为船舶纵荡速度,m/s;为船舶横荡速度,m/s;为船舶横摇角速度,m/s;为船舶艏摇角速度,rad/s;对应上标黑点表示对时间的导数,即加速度,rad/s。X为螺旋桨推力,N;(),()为航速时的线性和三次方项横摇阻尼系数;K为舵增益系数;T为微分控制常数;T舵机常数。
为船舶质量,kg;I、I和I分别为横摇惯性矩、纵摇惯性矩和艏摇惯性矩,kg·m。A、B、C为耦合系数;1:纵荡,2:横荡,3:垂荡,4:横摇,5:纵摇,6:艏摇。
1.3 船体力
船体力X,Y,N和K表达式如下:



公式(11)至(14)中的操纵性导数标准表达式,参见文献[12]。
1.4 螺旋桨推力和静水阻力
纵荡方程中的双螺旋桨推力的表达式如下:

式中:n为螺旋桨转速,r/s;D为螺旋桨直径,m;t为螺旋桨推力减额分数;K为螺旋桨推力系数;J为螺旋桨的进速系数;w为螺旋桨伴流分数。
纵荡方程中船体静水阻力()的表达式如下:

式中:为水密度,kg/m;S为船舶湿表面积,m;C为船舶总阻力系数;L为船舶垂线间长,m;为重力加速度,m/s。
1.5 舵 力
舵力表达式采用文献[27]标准MMG方程里的表达式,双舵的舵力X,Y,N表达式参考文献[28] (S:右舷;P:左舷)。

其中:

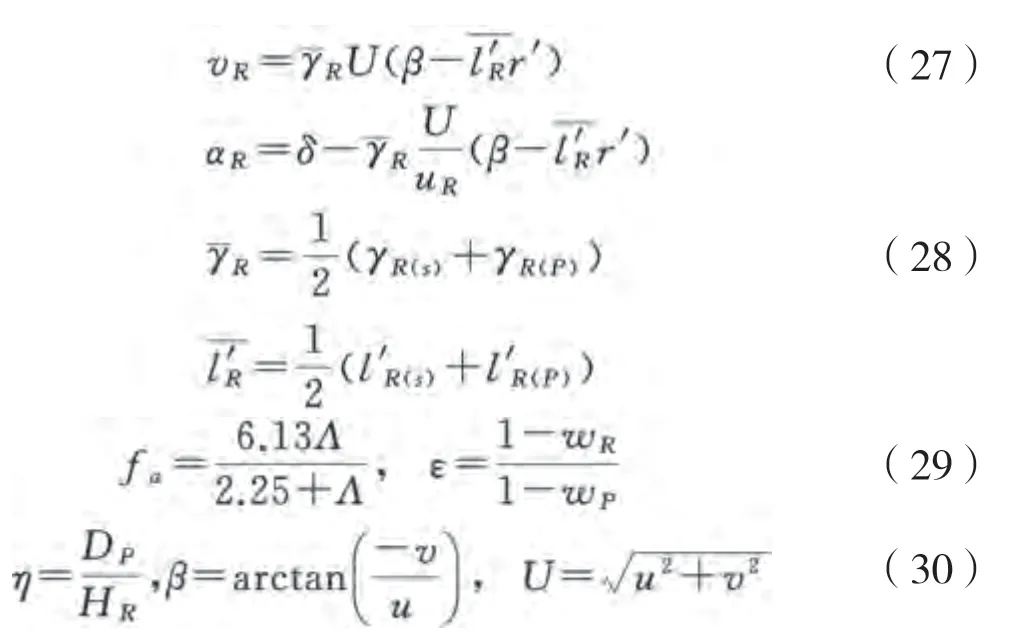

1.6 波浪力
波浪力主要包括F-K力和绕射力,各方向波浪力计算公式如下所示:

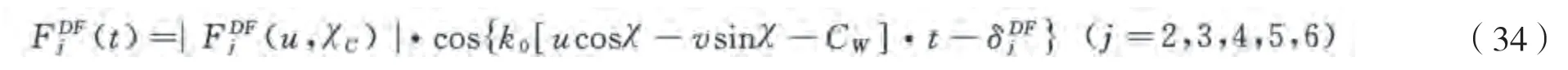

2 模型介绍
本文以ONR内倾船为目标船型,开展尾斜浪纯稳性丧失研究。ONR内倾船的主要参数和横剖面图如表1和图2所示。

表1 船型主要参数

图2 船体横剖面图
3 结果与分析
计算工况:波长与船长比/L为1.25,波陡/为0.05,船舶航向为30°,航速从0.2到临界倾覆速度。纯稳性丧失导致最大横摇角度六自由度计算结果与试验结果对比情况如下页图3所示,整体趋势比较吻合。
下页图4和图5给出了=0.225和=0.275试验测 量的时域结果。在航速低于目前衡准规定的=0.24时,横摇运动为稳定周期运动,如图4所示。在航速接近倾覆的临界航速时,出现不稳定横摇,如 图5所示。该试验结果为中国船舶科学研究中心耐波性水池测量,水池长69 m、宽40 m,船模 3.8 m,在有限长度的耐波性水池中,在航速接近倾覆的临界航速时,不同航次最大横摇角并不一致,同一航次会出现不稳定横摇运动,横摇最大值存在不确定性,图3给出组最大横摇角度试验测量 结果。
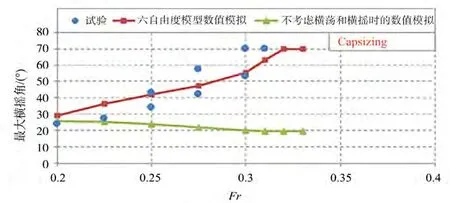
图3 尾斜浪中最大横摇角计算结果和试验结果比较(H/λ=0.05,λ/Lpp=1.25,χ=30°)
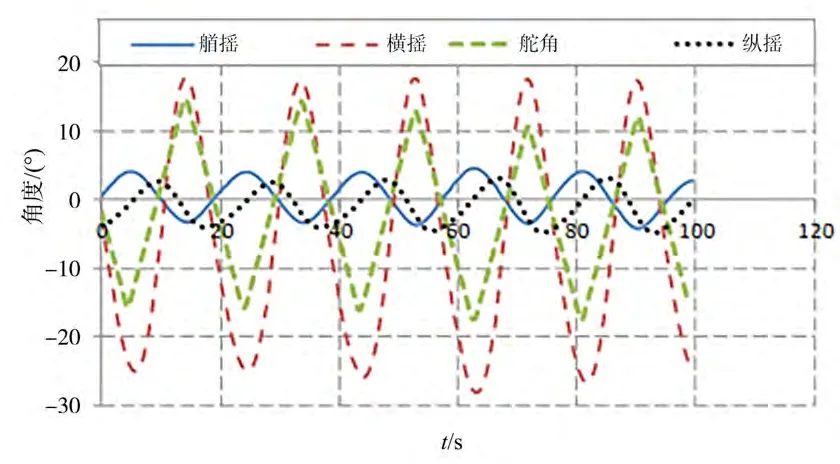
图4 尾斜浪中纯稳性丧失试验结果(Fr=0.225,H/λ=0.05,λ/Lpp=1.25,χ=30°)
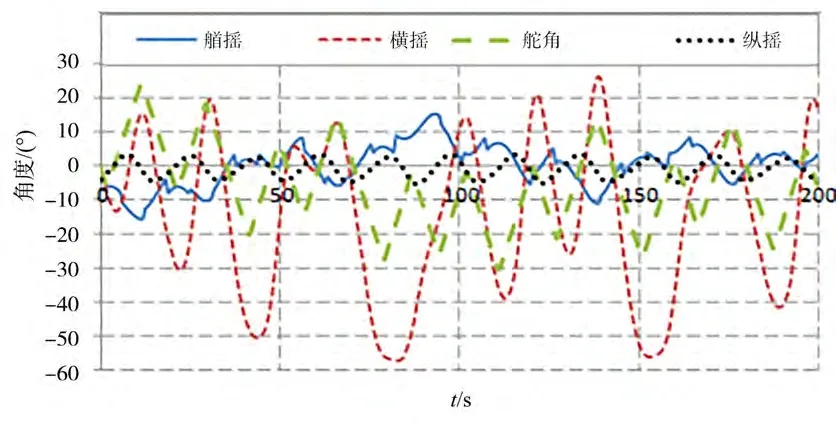
图5 尾斜浪中纯稳性丧失试验结果(Fr=0.275,H/λ=0.05,λ/Lpp=1.25,χ=30°)
图6 至图11给出了=0.2、0.225、0.25、0.275、0.3和0.33的时域计算结果。随着航速增加,遭遇周期变大,实际航速变化振幅变大,停留在波峰附近的时间变长。图12给出了=0.3、固定横倾10°,不考虑艏摇和横荡时的复原力臂GZ的变化规律。可以看出,在航速接近倾覆的临界航速时,船舯位于波峰附近时间明显变长,复原力丧失的时间变长。这是纯稳性丧失导致大幅横摇,甚至倾覆的一个重要原因。鲁江等指出横荡、艏摇在横摇方向的离心力贡献是尾斜浪中纯稳性丧失发生大幅横摇一个重要原因。图3给出了不考虑横荡和艏摇运动的数值模拟结果,在纯稳性丧失发生的航速范围内横摇振幅远小于试验结果,进一步证明横荡和艏摇在横摇方向的贡献是尾斜浪中纯稳性丧失发生大幅横摇的一个重要原因。

图6 斜浪中纯稳性丧失计算结果(Fr=0.2,H/λ=0.05,λ/Lpp=1.25,χ=30°)
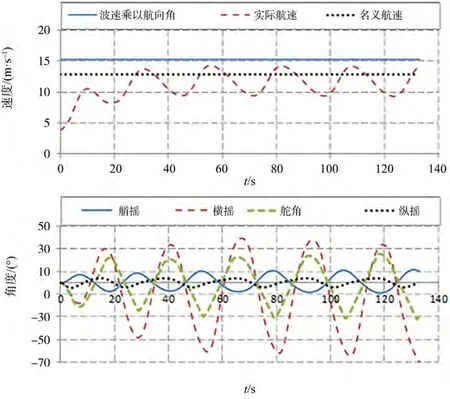
图11 尾斜浪中纯稳性丧失计算结果(Fr=0.33,H/λ=0.05,λ/Lpp=1.25,χ=30°)

图12 尾斜浪中复原力臂变化规律 (Fr=0.3,H/λ=0.05,λ/Lpp=1.25,χ=30°,Roll=10°)
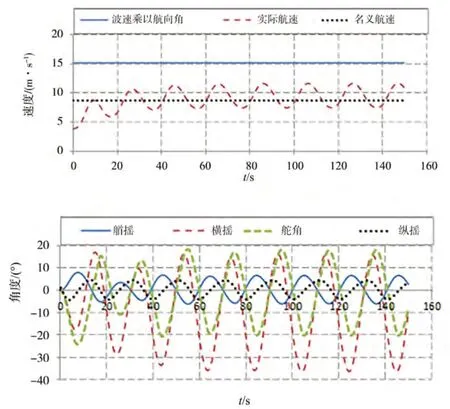
图7 尾斜浪中纯稳性丧失计算结果(Fr=0.225,H/λ=0.05,λ/Lpp=1.25,χ=30°)

图8 尾斜浪中纯稳性丧失计算结果(Fr=0.25,H/λ=0.05,λ/Lpp=1.25,χ=30°)

图9 尾斜浪中纯稳性丧失计算结果(Fr=0.275,H/λ=0.05,λ/Lpp=1.25,χ=30°)
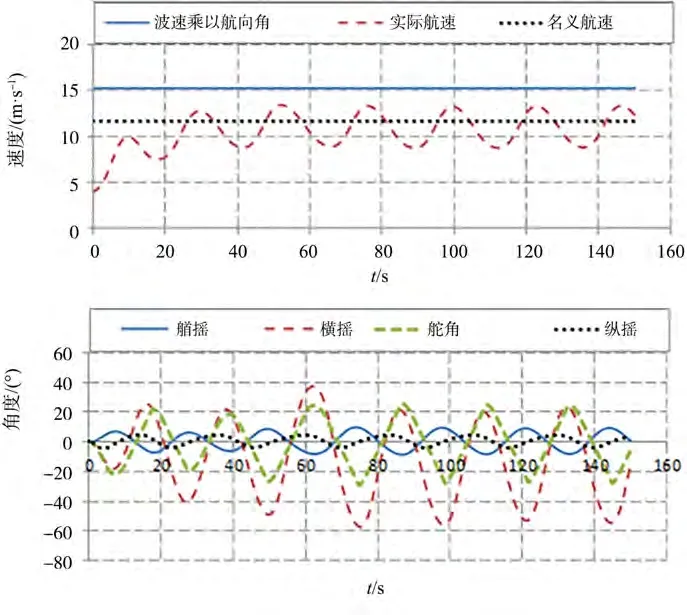
图10 尾斜浪中纯稳性丧失计算结果(Fr=0.3,H/λ=0.05,λ/Lpp=1.25,χ=30°)
4 结 论
基于内倾船型六自由度纯稳性丧失数学模型计算结果和试验结果,可以得出以下结论:
(1)本文构建的六自由度运动耦合的数学模型能够定量预报尾斜浪规则波中纯稳性丧失导致的大幅横摇和倾覆;
(2)横荡和艏摇运动在横摇方向的耦合力矩是尾斜浪纯稳性丧失导致大幅横摇失稳的一个重要原因。
5 致 谢
本文部分研究内容和ONR船型参数来自日本大阪大学梅田直哉教授,本文工作得到工业和信息化部高技术船舶项目资助和船舶二代稳性研究项目组的支持,对上述机构和个人表示诚挚的感谢。
