水下拖曳航行器水动力和拖缆姿态仿真分析

侯二虎　杜敏　汪小勇　吴国伟　秦玉峰

摘要：水下拖曳航行器是被广泛应用的水下监测平台。为掌握水下拖曳航行器的水动力及其拖揽姿态，文章通过CFD仿真分析计算其零攻角下的阻力系数，并通过多刚体-球铰模型建立其运动数学模型，分析不同航速下拖曳系统的总拉力、拖缆长度和航行器位置等的参数变化。研究结果表明：随着船舶航速的变化，拖曳系统各项参数变化的差别很大;在200 m深度时，6 kn航速相比4 kn航速的总拉力增加73%，而所需的拖缆长度仅增加1%。该数学模型可对不同航速下的水下拖曳系统的总拉力和拖缆姿态等做出预测，为拖曳系统设计提供技术支撑。

关键词：水下拖曳系统;拖缆;水下姿态;仿真分析;航速

中图分类号：P715.5 文献标志码：A 文章编号：1005-9857（2020）02-0074-04

Abstract：The underwater towing vehicle is a widely used underwater monitoring platform.In order to study its hydrodynamic and attitude prediction problems，the drag coefficient under the zero angle of attack of the aircraft was obtained through CFD simulation analysis，and the mathematical model of its motion was established by the “multi rigid bodyball joint” model，the parameters such as the total pulling force，the length of the cable and the position of the aircraft at different speeds were analyzed.The results showed that the different parameters of the towing system varied greatly with the ship′s speed changed.Under the depth of 200 m，with ship speed of 6 knots，the total pulling force of the towing system increased by 73% and the required length of cable increased by only 1% compared to ship speed of 4 knots.The mathematical model proposed in this paper can predict the total pulling force of the towing system and the shape of the cable at different speeds，and provide technical support for the design of the towing system.

Key words：Underwater towing system，Towed cable，Underwater attitude，Simulation analysis，Speed

0 引言

水下拖曳航行器亦稱水下拖曳系统，被广泛应用于海洋、内河和湖泊的水下监测，在水下环境调查和监测中发挥多种用途。随着海洋开发的日益深入，水下拖曳航行器发挥的作用越来越重要，海洋拖曳系统的相关研究成为现代海洋开发与应用的重要课题之一[1]。

拖曳系统通常由拖曳拖缆以及被动或可控的水下拖曳体组成，准确描述拖缆和拖曳体的水动力姿态是准确模拟拖曳系统水动力性能的关键[2]。皮德福等[3]通过建立拖曳系统水下拖缆的平面形状和张力的二维数学模型，计算水下拖曳系统在不同航速下的姿态;苑志江等[4]针对海洋拖曳系统建立运动计算模型，提取影响系统稳定姿态的4个关键因素，并分析各因素对系统稳定姿态的影响;杨智栋等[5]采用集中质量法建立拖缆的运动方程，分析水下航行器运动过程中拖缆的长度及其作用力的变化;李志印[6]对水下拖曳系统的流体动力参数进行CFD分析，通过Fluent语言和Fortran语言的混编和对接，实现对拖曳体的水下动态模拟。本研究针对水下拖曳航行器的流体动力参数和不同航速下的拖缆姿态进行仿真分析，对不同深度下的运动工况给出所需缆长和拖缆姿态等结果，为水下拖曳系统设计提供技术支撑。

1 数学模型

1.1 坐标系

由于航行器关于纵平面对称，计算区域取航行器的50%，并采用对称模型计算，计算区域长为35 m、半径为5 m。求解器采用基于压力式的定常算法。湍流模型为标准kepsilon模型，该模型是目前应用最为广泛的湍流模型。近壁面处理选择标准壁面函数法。海水密度视为均匀密度，即1 025 kg/m3。

在靠近航行器的区域采用加密网格处理方法，加密区域为包裹航行器的直径为1 m的圆柱体，长度选取航行器的前1 m和后4 m，加密区域内的最小网格间距为1 mm。

入口处边界条件设为速度入口，出口为压力出口[10]，具体边界条件设置如表1所示。

航行器在计算区域内的计算工况为零攻角，采用航行器的50%进行仿真计算，得出所受阻力为26 N，全部阻力即为52 N，可得出航行器在零攻角下的阻力系数为0.17。

3 拖缆姿态

分别计算6 kn和4 kn航速的不同下放深度的拖缆姿态。未考虑海流速度，拖缆参数按钢缆计算。下放深度分别为50 m、100 m和200 m，坐标原点位于海平面，船舶沿X轴正向航行，Z方向为水深，船舶拖曳点位于原点铅垂上方5 m处。

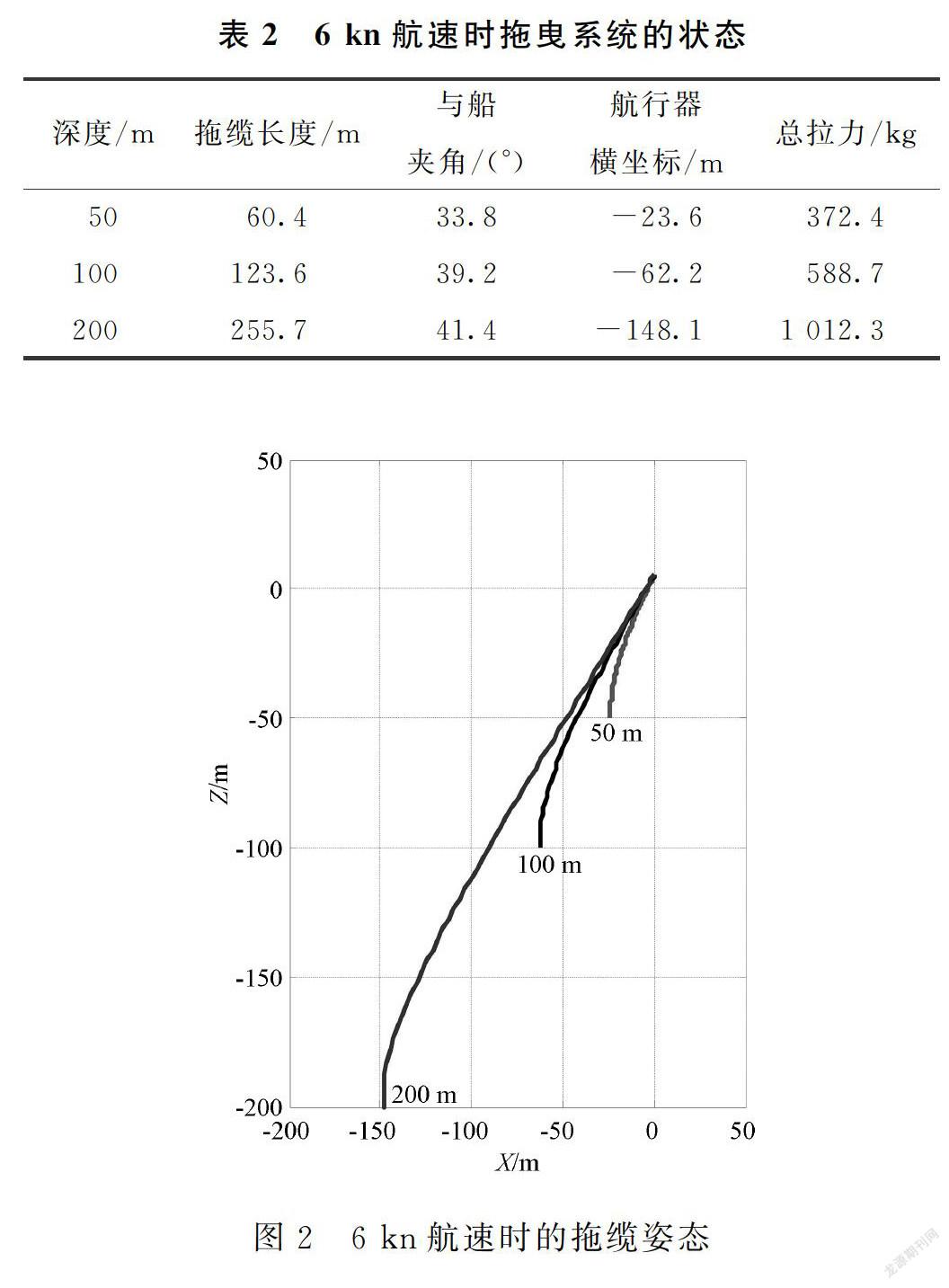
6 kn航速時拖曳系统的状态如表2所示，拖缆姿态如图2所示。

由表2可以看出，6 kn航速时，随着航行器深度的增加，拖曳系统各部分的状态均发生变化。由于船速的存在，所需拖缆的长度随深度的增加而增加：50 m定深时，拖缆长度比深度增加20.8%;100 m定深时，拖缆长度比深度增加23.6%;200 m定深时，拖缆长度比深度增加27.9%。所需拉力也有很大幅度的增加，200 m定深时所需拉力比50 m定深时增加171.8%。变化程度最小的是拖缆与船夹角，200 m定深时夹角比50 m定深时增加22.5%。由图2可直观地获取拖缆的最终姿态，结合航行器的横坐标即可确定航行器的最终位置。

4 kn航速时拖曳系统的状态如表3所示，拖缆姿态如图3所示。

由表3可以看出，4 kn航速时拖曳系统的整体状态与6 kn航速时类似。由于航速减小，拖缆长度、与船夹角和最终拉力等参数均有不同程度的减小。随着深度的增加，总拉力由50 m定深时的269.8 kg增加至200 m定深时的586.7 kg，增加117.5%。拖缆长度在50 m定深时为56.5 m，相比深度增加13%，而在200 m定深时相比深度增加26.7%。

对比6 kn航速和4 kn航速下的计算结果可以看出，随着航速的增加，船舶拖曳点处的总拉力和拖缆长度等参数均有变化。50 m深度时，6 kn航速比4 kn航速所需拉力增加38%，拖缆长度增加7%;100 m深度时，6 kn航速比4 kn航速所需拉力增加58%，拖缆长度增加9%;200 m深度时，6 kn航速比4 kn航速所需拉力增加73%，拖缆长度增加1%。3种深度下航行器横坐标的增加幅度分别为79%、54%和35%，与船夹角的增加幅度分别为50%、25%和13%。因此，航速变化对拖曳系统总拉力变化的影响最显著，且总拉力的增加幅度随航速增加而增加，其余参数的增加幅度随航速增加而减小。

4 结语

本研究建立水下拖曳航行器拖缆流体水动力和拖缆姿态的数学模型，并通过该模型对6 kn和4 kn航速下拖曳系统的姿态和受力进行仿真分析，研究结果表明：①随着航速的增加，拖曳系统的各项参数均有所增加，但增加幅度不同，其中总拉力的增加幅度增加，而拖缆长度、与船夹角和航行器横坐标的增加幅度减小;②总拉力的增加幅度非常明显，在200 m深度时，6 kn航速相比4 kn航速的总拉力增加73%，而拖缆长度仅增加1%。

本研究建立的数学模型可对水下拖曳航行器在不同航速时的流体动力及其所处位置做出预测，为拖曳系统的设计工作提供技术支撑。需要说明的是，本研究仅针对匀速航行时的拖曳系统，且将海水视作均匀密度的介质。未来研究工作应考虑实际海洋环境的潮流、波浪、温度和盐度等因素的变化对拖曳系统的影响。

参考文献

[1] 苑志江，金良安，田恒斗，等.海洋拖曳系统的水动力理论与控制技术研究综述[J].科学技术与工程，2013，13（2）：408-415.

[2] 李志印，吴家鸣.水下拖曳系统水动力特性的计算流体力学分析[J].中国造船，2007，48（2）：9-19.

[3] 皮德福，宋保维，李正，等.水下拖曳系统稳定姿态仿真计算[J].系统仿真学报，2005，17（10）：2358-2359.

[4] 苑志江，金良安，迟卫，等.海洋拖曳系统稳定姿态的影响因素研究[J].科学技术与工程，2013，13（5）：1127-1134.

[5] 杨智栋，潘光，杜晓旭.变缆长拖缆AUV纵向运动建模与仿真[J].水下无人系统学报，2014，22（1）：14-19.

[6] 李志印.水下拖曳系统的流体动力CFD分析[D].广州：华南理工大学，2005.

[7] 陈永华.波浪驱动式海洋要素垂直剖面测量系统关键技术[D].青岛：中国科学院研究生院（海洋研究所），2008.

[8] 姜静波.海洋剖面测量系统形态模拟及仿真研究[D].青岛：中国科学院研究生院（海洋研究所），2008.

[9] DEWEY R K.Mooring design and dynamics：a Matlab package for designing and analyzing oceanographic moorings[J].Marine Models，1999，1（1/4）：103-157.

[10] 朱红钧，林元华，谢龙汉.Fluent流体分析及仿真实用教程[M].1版.北京：人民邮电出版社，2010.