基于全非线性流函数理论的规则波中船舶 大幅运动弱非线性数值模型研究

马 山 赵彬彬 段文洋 刘豆豆 刘金纯 何 强

（哈尔滨工程大学 船舶工程学院 哈尔滨 150001）

0 引 言

在较为恶劣的海况中，当船舶以较高航速顶浪航行时常会遭遇到大幅的非线性垂向运动，典型船型包括集装箱船、驱逐舰和一些客船，这些船舶通常在首尾部具有显著的外飘。在船舶恶劣海况下非线性摇荡运动评估中，弱非线性方法获得了广泛应用，该类方法具有很好的计算效率和精度。在该种方法中，作用在船体上的入射波主干扰力（Froude-Krylov力，下文简称F-K力）和静水恢复力是主要考虑的非线性流体载荷，通常在入射波面以下的瞬时船体湿表面上评估，线性波浪理论模型常用来进行船体非线性F-K力的计算。然而不容忽视的事实是在高海况下海浪本身的非线性效应较为明显，典型的就是波面的尖峰坦谷特征。RAJENDRAN研究了二阶Stokes波浪理论效应对恶劣海况下船舶垂向非线性运动的影响，其中入射波压力采用包括二阶入射速度势的波浪理论来计算，通过在瞬时船体湿表面以下进行二阶入射波压力积分来计算非线性F-K力，作者发现恶劣海况下船舶纵摇运动峰值与模型试验的对比相对于线性波浪符合的要更好。

对于具有外飘的船型（如集装箱船）在较高海况的高航速下，会受到砰击载荷作用，且砰击载荷较为复杂，一般仅持续很短时间。关于砰击的研究始于VON KARMAN。他提出了水上飞机着陆时砰击力载荷的计算方法，建立了二维楔形体入水砰击理论。WAGNER进一步发展了 二维楔形体砰击力的计算方法。后来，许多学者使用WAGNER的方法来计算砰击力。除了WAGNER模型估算船舶砰击力外，动量冲击理论也经常被使用。陶智祥等用动量冲击理论和WAGNER冲击理论计算了船首外飘砰击产生的船体砰击压力和剖面弯矩，计算结果与模型试验结果吻合良好。他们在研究中提到，船首外飘砰击的持续时间相对较长，用动量冲击理论来估计船首外飘砰击是合适的。JIAO等在开发数值模型以计算大型船舶在恶劣波浪中的非线性水弹性响应时，应用动量冲击理论来估计外飘砰击载荷。

从以往对非线性船舶运动分析的研究中发现，很少有研究系统地讨论全非线性波浪对F-K力和船舶运动的影响。此外，虽然动量冲击理论已被用于分析船舶砰击引起的整体波浪载荷，但是这种砰击模型对垂向剖面砰击载荷本身及其对船舶整体运动评估的精确性并没有详细讨论。基于这两点，本文采用全非线性波浪理论来模拟入射波浪场，其目的是提高在恶劣海况下非线性F-K力和船舶运动响应的数值精度，然后结合非线性波浪模型建立船舶大振幅运动的弱非线性模型。此外，文中还引入动量冲击理论来估算船舶所受的剖面外飘砰击力，对S175集装箱船的全非线性F-K波浪力、垂向剖面上的外飘砰击载荷和船舶运动进行了数值模拟，并将数值结果与线性波浪模型、CFD结果和模型试验的结果进行了比较和验证。

1 采用弱非线性方法的非线性垂向 船舶运动预报

假设船舶以航速运动，当前主要关注顶浪中的垂向运动。建立随船平动坐标系，其中经过船舶重心铅垂向上，轴指向船首，原点位于静水面上，采用弱非线性模型求解船舶的非线性摇荡运动。数值模型中，船舶摇荡运动辐射和绕射水动力采用线性势流方法求解，而入射波主干扰力和静水回复力在入射波面夏瞬时船体湿表面积分获得，引入动量砰击载荷模型评估了船舶砰击力对总体运动的影响，对船舶运动和水动力载荷模型简述如下。

1.1 波浪中的垂向运动方程

顶浪中的垂荡和纵摇运动方程表述如下。

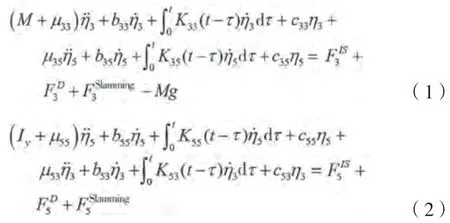
式中：是船体质量，kg；I是船体绕过重心轴的纵摇转动惯量，kg·m；、Slamming表示作用在船体上的垂向和纵摇方向的砰击载荷合力，N。上述的运动方程采用四阶龙格-库塔法求解。

1.2 辐射水动力

船体上的辐射力采用辐射脉冲响应函数的卷积积分来表示：

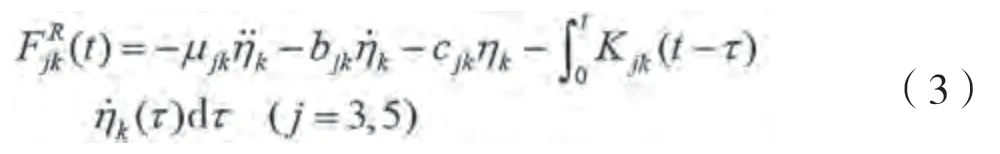
式中：η（=3.5）表示船舶的垂荡和纵摇运动响应；μ表示船体无穷大频率附加质量；b、c表示无限大频率辐射阻尼和恢复力系数；K是由于船舶脉冲运动引起的辐射力脉冲响应函数，可以采用频域水动力系数表示如下：

式中：ω是规则波中船舶摇荡运动的遭遇频率；B是频域中的辐射阻尼系数。

马山等基于频域中的切片理论的辐射水动力系数，发展了一致性算法评估μ、b、c和K，这里不再详述。

1.3 绕射水动力

在时域分析中，绕射力也采用卷积积分来表示，结合BALLARD等的分析，绕射力表示为：

式中：()是船舶重心处的入射波面位移，m；h()是绕射力脉冲响应函数，表示如下：

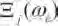
1.4 非线性入射波主干扰力和静水恢复力

入射波浪力和静水压力采用在瞬时船体湿表面上积分获得。

式中：P表示船体湿表面入射波压力，N/m；()表示入射波面以下的瞬时船体湿表面，采用离散的船体小面元几何来表示。在船体运动求解的每个时间步，穿越入射波面的面元要进一步剖分，细节请参见胡开业等论文。

对于非线性摇荡运动的评估，F-K力是主要的非线性流体载荷。高海况下波浪有显著的非线性特征，包括波面的峰谷非对称特性、流体压力和速度的非线性表达，这些采用线性/弱非线性理论不能很好的描述。为了研究非线性波浪模型对船体受到的非线性F-K力和船体运动的影响，本文应用流函数理论进行了研究。该理论是一种深水规则波全非线性的波浪理论，可以在很大范围内描述非线性波陡的影响。

建立坐标系，以波浪传播相速度运动，在这个坐标系下描述波浪场表示如下：

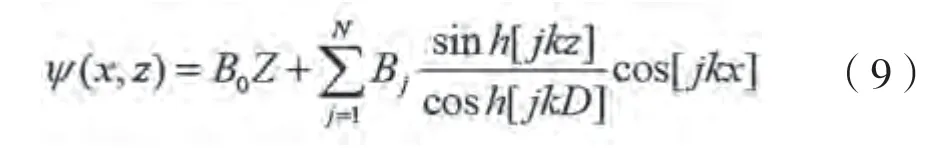
式中：，B，=1，2是未知常数；是水深，m；是未知波数。方程（9）中的未知量与包括波面位移()、波浪传播的相速度， 以及常数和一同求解。具体请查看文献[10]。

一旦求解方程（9），流体粒子速度表示如下：

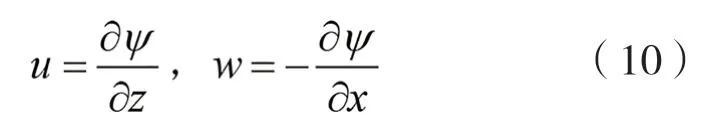
在大地坐标系下，流体运动是非定常的，非定常的流体速度分量为(，，)、(，，)，可表示为：(，，)=+(，)，(，，)=(，)。

流体压力表达为：

式中：是一常数，通过流函数理论的数值解法得到。

深水中的线性规则波在随船平动坐标系下表达如下：

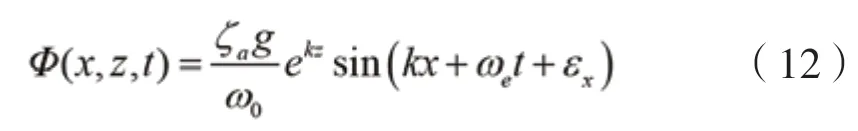
式中：ζ是线性入射波幅， m；是圆频率，rad/s；是波数；ω=ω是顶浪中的遭遇频率；ε= -kX表示初始相位角，rad；X表示船舶重心在大地坐标系下的初始位置，对应的波形表示如下：

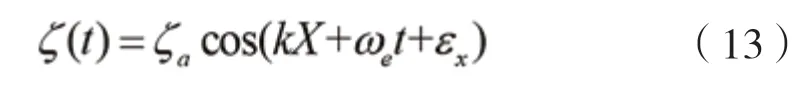
对于线性入射波浪压力，可以通过伯努利方程得到。为了考虑非线性效应的影响，这里采用了Wheeler拉伸模型进行压力修正，入射波压力表达如下：

1.5 船体外飘砰击力

对于首尾部外飘型船舶，在较为恶劣海况下高速航行时，会受到外飘砰击载荷作用，按照动量冲击理论，船体剖面的流体砰击载荷（戴仰山等）可计算如下：

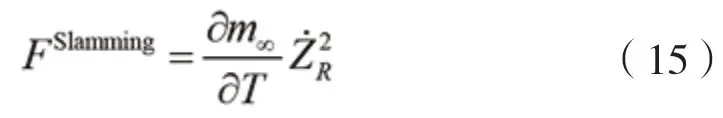
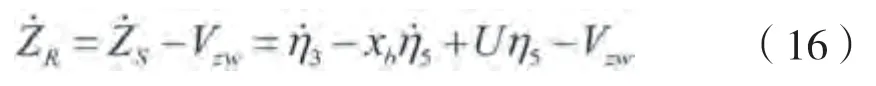
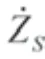
式中：X，X表示船体尾部和首部的纵向位置。

2 数值结果与讨论

基于上面的数值模型，针对S175集装箱船标模开展了计算分析，并与公开发表的模型试验开展了对比分析。下页表1给出了船模主尺度。

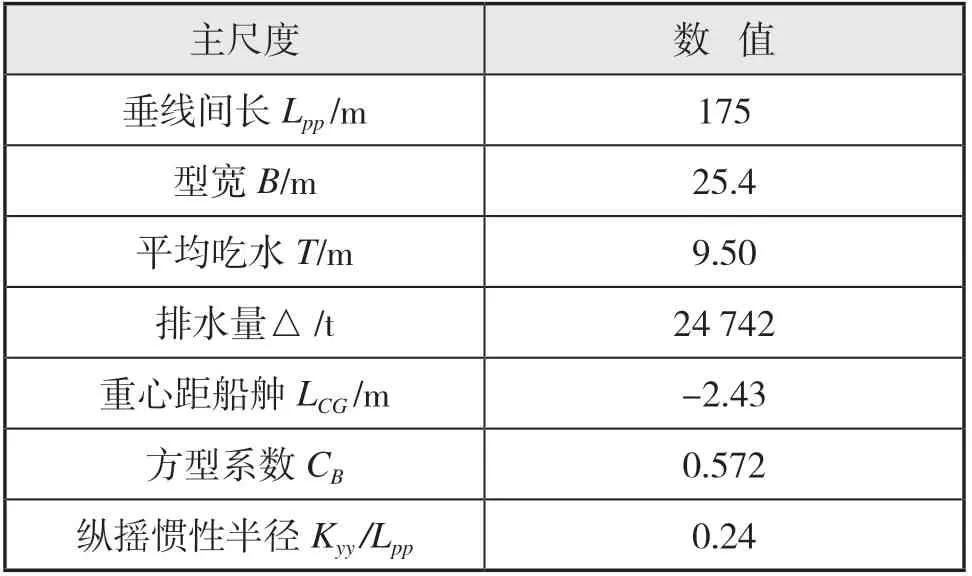
表1 S175集装箱船主尺度

S715的线型如下图2所示。

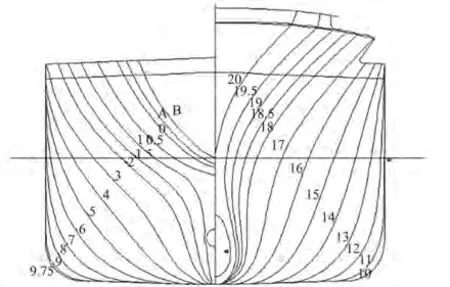
图2 S175集装箱船型线

2.1 数值模型验证

本文中，动量砰击模型用于估算船体剖面砰击力，选取AARSNES的剖面砰击力试验进行验证，作者开展了船首剖面不同落体高度下的自由落体砰击试验。本文砰击力采用公式（15）进行评估，垂向落体运动方程采用如下公式描述。

式中：是落体质量，按文献取为261 kg；m是静水面以下落体结构的瞬时垂向附加质量，kg；本文中的落体高度取= 0.318 m；表示静水面以下的落体瞬时浮力，N。

数值模拟时从剖面底部刚接触水面开始模拟，对应的落体初始速度取2.43 m/s，落体剖面轮廓如图3所示。

图3 AARSNES落体试验中用到的船体剖面

剖面最大宽度和深度分别取320 mm和240 mm。通过求解方程（18），剖面的垂向水动力载荷与落体速度如图4所示。

图4 船体剖面在落体高度h=0.318 m的垂向水动力和落体速度结果

从中可以看出：垂向水动力载荷整体上与试验符合较好，但峰值位置相对于模型试验有0.008 s的滞后。对于垂向落体速度，在0.04 s以后，数值结果的速度改变相对于模型试验偏小一些。本文的数值模型中没有考虑砰击过程中的水体上涌现象，而在模型试验中，该效应可能影响了下落体撞击水面的过程，导致最大砰击力载荷相对于本文的数值模型更早发生。总的来说，本文采用的动力砰击模型可以提供波浪撞击载荷的定量预报。

为了进一步研究船体剖面入水中的砰击过程，采用黏流分析软件StarCCM+开展了S175集装箱船剖面19站的入水砰击分析，数值模拟缩尺比是1∶40，对应的模型尺度落体速度是1.3 m/s（实际长度是 8.22 m/s）。该剖面几何形状如图5所示，剖面最大垂向高度是476.5 mm，网格划分如图6所示。

图5 S175集装箱船19站的几何剖面

图6 剖面恒速入水的流体域网格设置

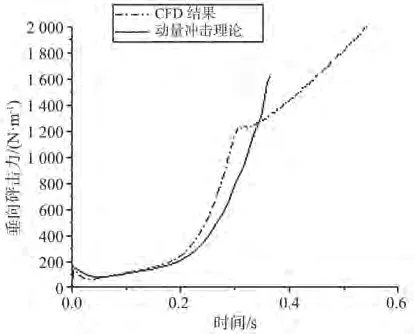
图7 S175集装箱船首部剖面以1.3 m/s入水的垂向砰击力

表2给出了计算参数和对应的每套网格的峰值砰击力情况。

表2 用于收敛性分析研究的网格数和局部砰击载荷

不同网格数间的砰击峰值载荷的相对变化和收敛率情况如下：

从中可以看出，收敛率满足0<R=ε/ε=0.58<9，表明对应的3套网格的砰击载荷满足单调收敛条件。因此，下面工况2的网格设置获得的砰击载荷用于开展与本文的动量定量砰击载荷模型的对比。对应的背景区网格数是23.7万，重叠区网格数是17.1万。采用高性能集群完成黏流CFD计算，采用单节点、32核、64 G内存获得图7的砰击载荷计算耗时5 h。

图7提供了单位长度的船体剖面恒速入水的总的垂向流体载荷，可发现在0.309 s之前动量砰击理论的结果相对于CFD（computational fluid dynamics)方法偏小些，但总体上与CFD结果较一致。在0.309 s以后，来自于 CFD 结果的载荷随时间变化率有所降低，而动量砰击理论的结果仍然增加。为了分析该现象，图8给出了砰击入水中的波面演化。

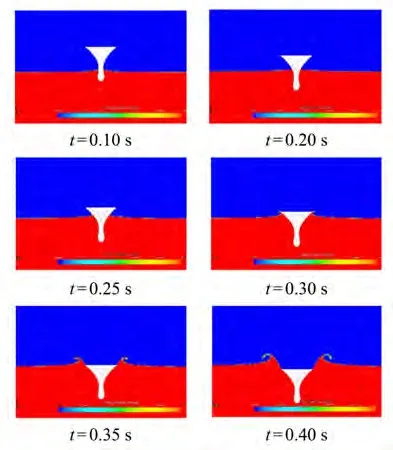
图8 入水过程中的自由液面演化

从中看出0.3 s之前的波面在浮体周围上涌：在0.3 s左右，自由面下的剖面宽度达到最大，船体剖面砰击载荷达到最大值；在0.3 s以后，从图7可看出流动分离在剖面顶部拐角发生，剖面砰击载荷增加的变化率降低。本文采用的砰击模型当前没有考虑入水中水面堆积抬升的影响，从而导致在剖面入水达最大宽度前砰击载荷偏小，同时没有合理反映流动分离以后时刻的砰击载荷。

下面，针对S175规则波中的非线性运动的幅值响应因子（response amplitude operater，RAO）与模型试验结果进行对比。线性STF切片理论结果同时也用于数值模型对比验证。

图9至下页图11给出了规则波顶浪2个入射波陡下一阶与二阶垂荡和纵摇运动幅值对比，结果以无因次化的波长船长比/L表示。垂荡和纵摇运动幅值分别用ζ和kζ无因次化，其中是线性入射波波数，ζ是线性入射波波幅。

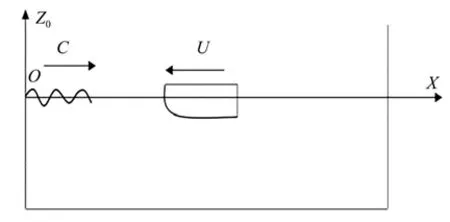
图1 全非线性顶浪规则波中求解非线性运动的大地坐标系OXZ

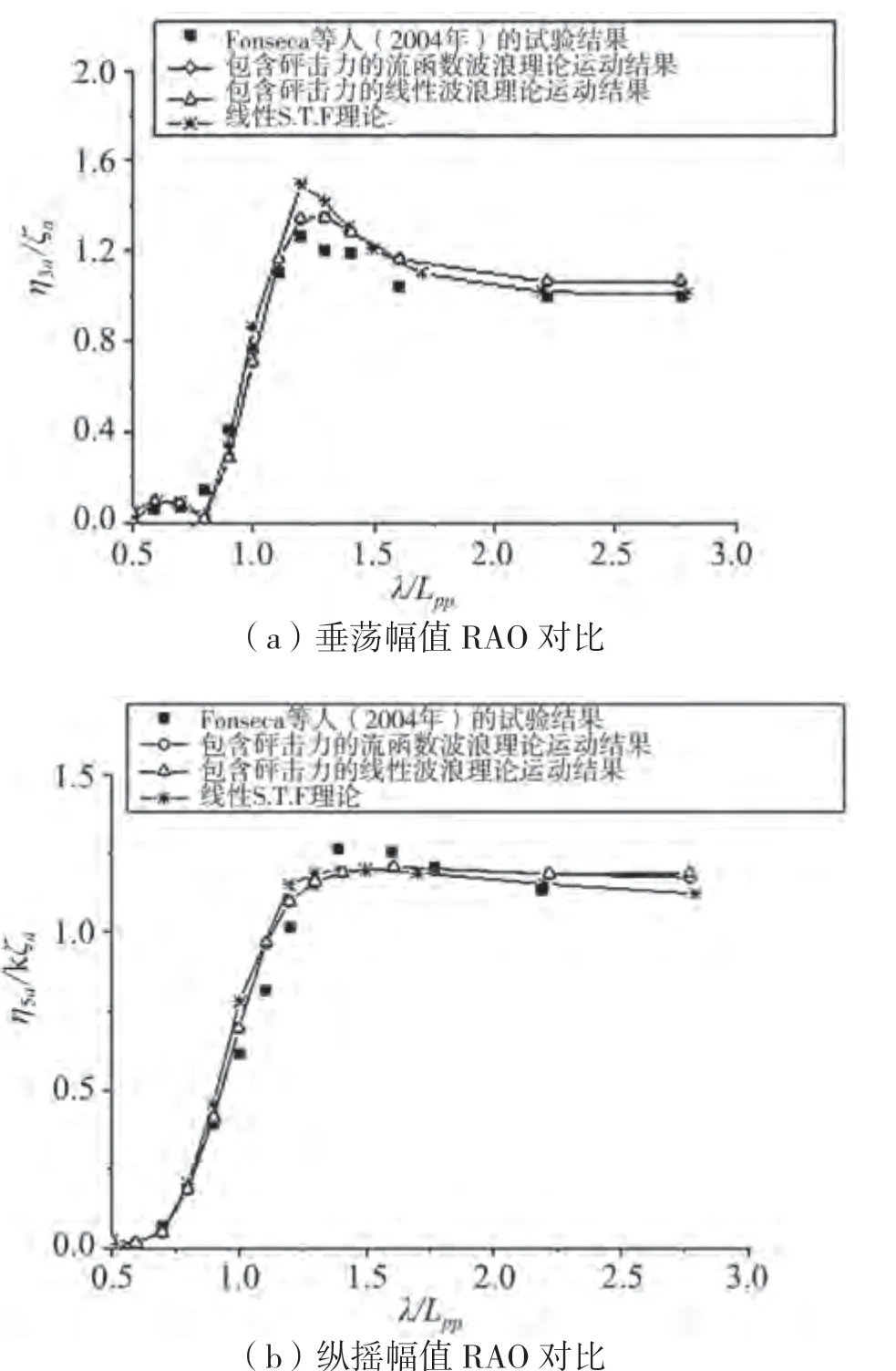
图9 顶浪规则波中一阶垂荡和纵摇运动幅值对比（Fr = 0.25，HW/λ=1/120）

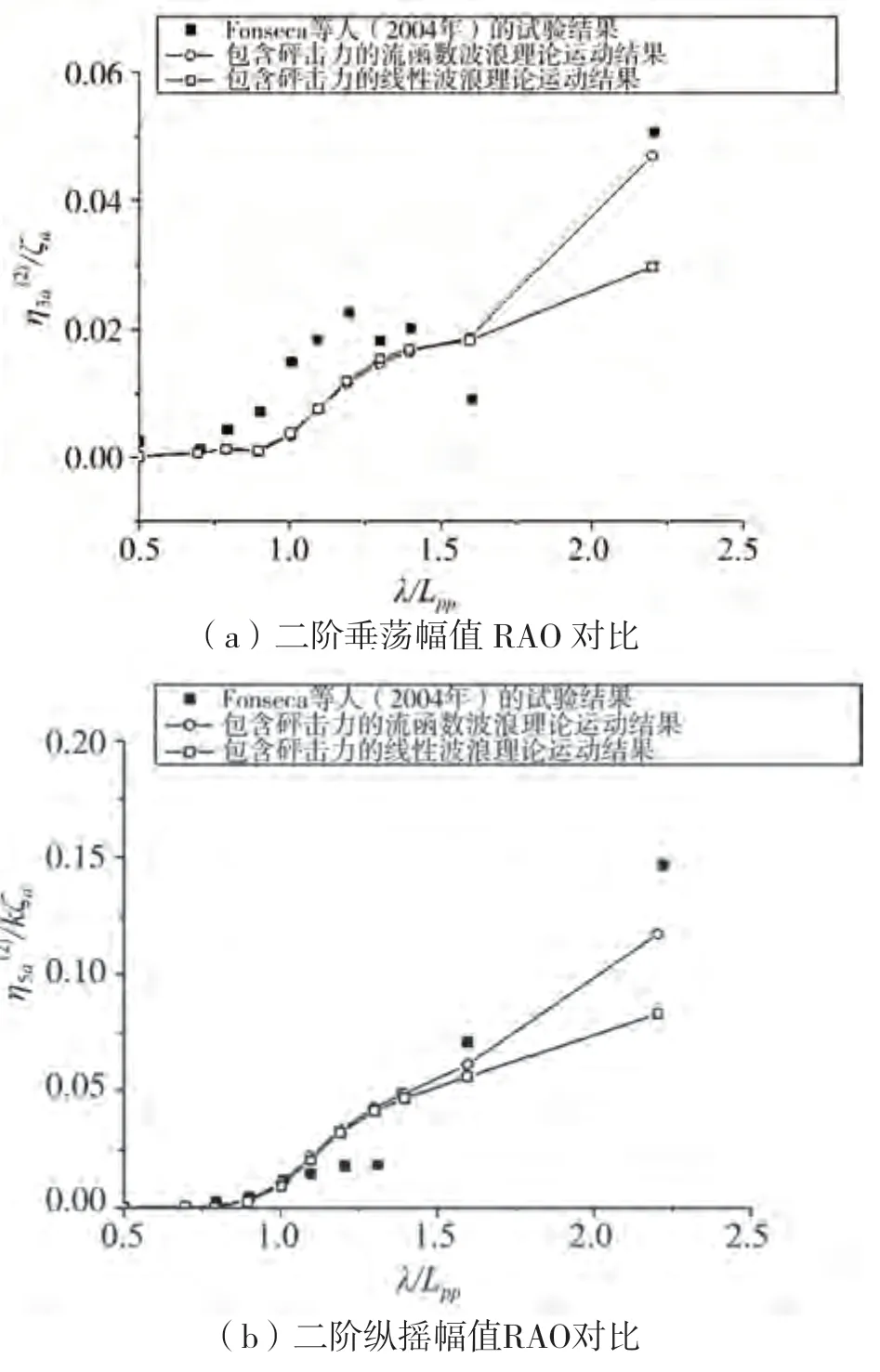
图11 顶浪规则波中二阶倍频垂荡和纵摇运动幅值对比（Fr=0.25，HW/λ=1/40）

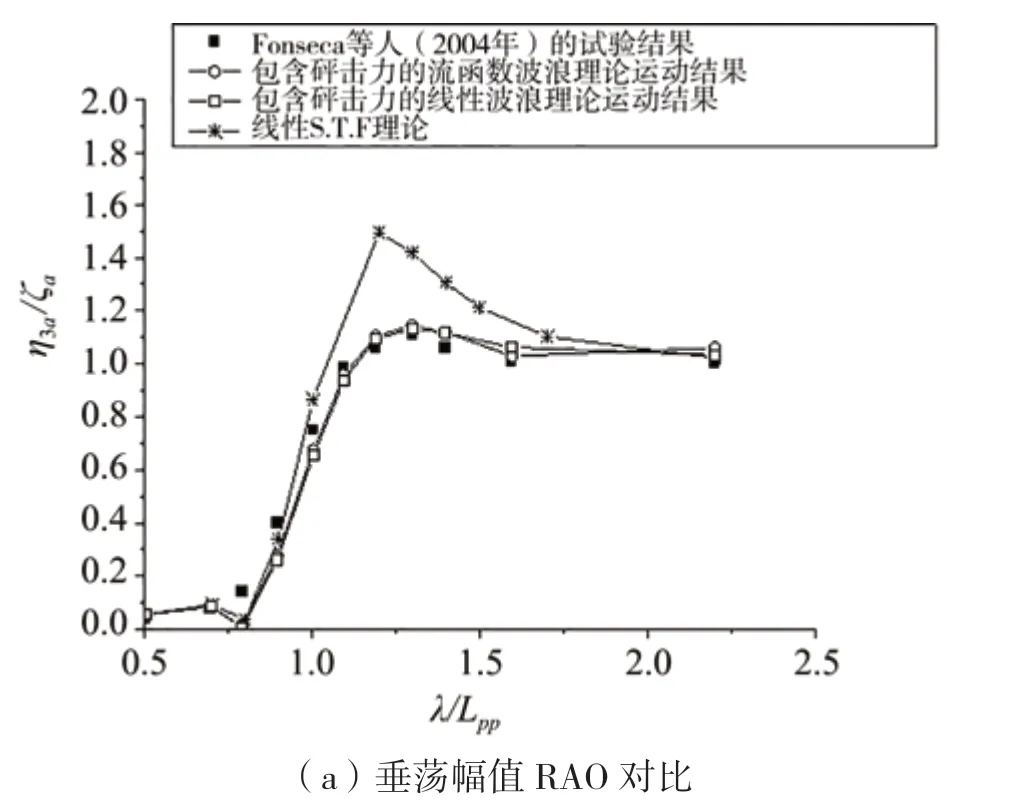
在图9～11结果中，采用对运动时间历程的最小二乘拟合公式（19）来获得运动幅值。

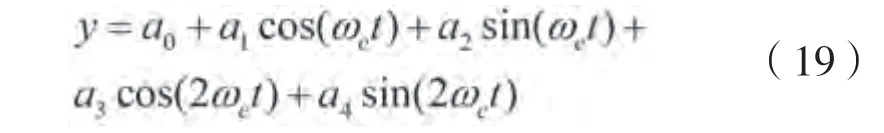
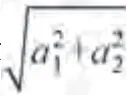
图9～10表明本文提出的弱非线性船舶运动模型可以有效改善规则波中一阶运动RAO幅值特别是共振运动峰值位置的预报精度。图11给出了二阶垂荡和纵摇运动峰值的预报结果，二阶运动幅值相对于一阶运动幅值小很多，数值可以提供与试验结果一致的预报精度，此外，在波长船长比＞2.2时，采用流函数波浪理论预报的垂荡和纵摇运动二阶幅值与试验结果符合的更好一些。

为了进一步检验本文的数值模型，采用流函数波浪模型与线性波浪模型开展了波长船长比1.0、1.2和1.4的3个典型波长不同波陡下顶浪中垂向运动计算。结果如图12～14所示，最大的入射波陡/在0.03左右。

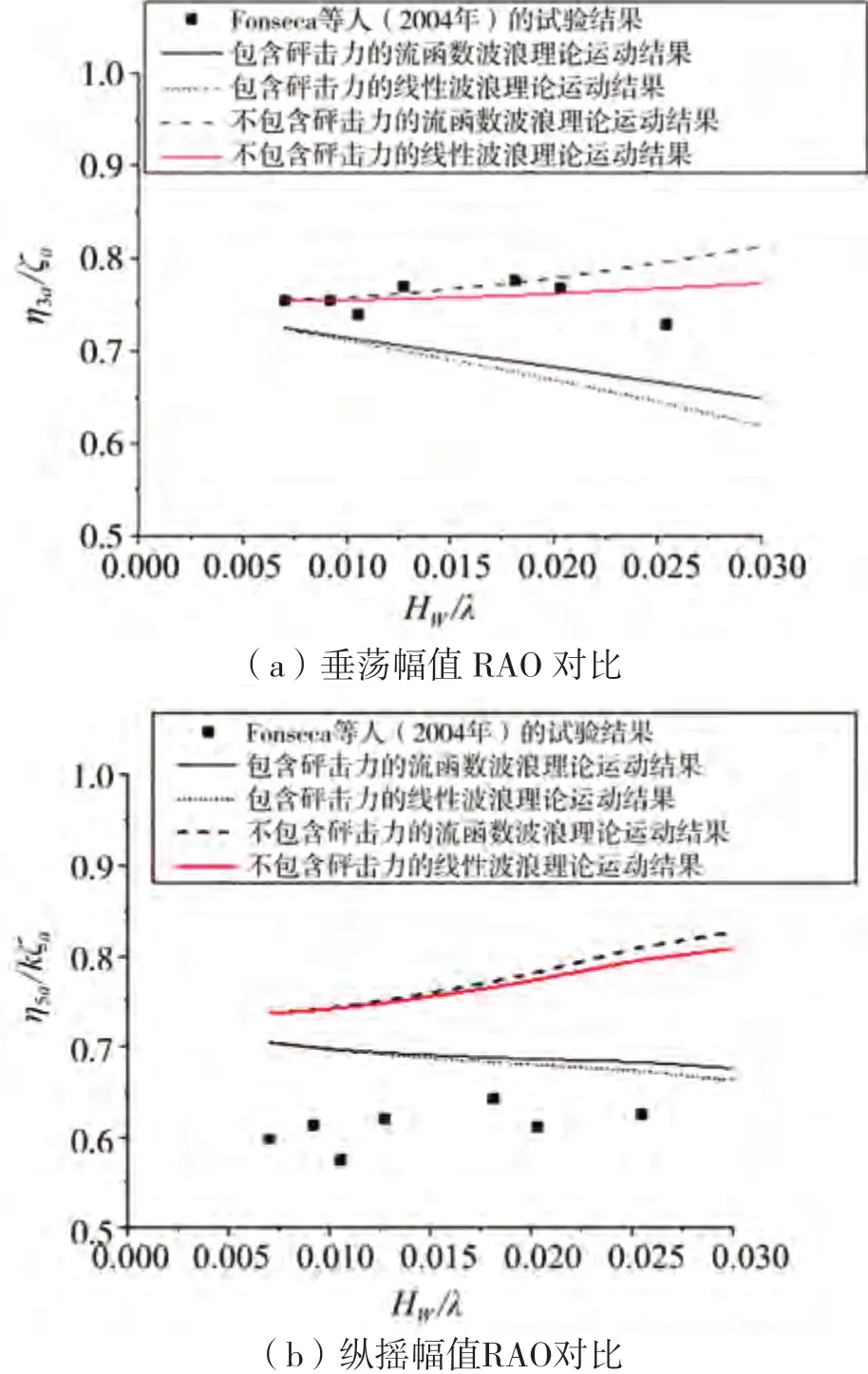
图12 顶浪中一阶垂荡和纵摇运动幅RAO对比（Fr=0.25，λ/Lpp=1.0）

图12～14中给出了结果对比，图中结果给出了3个典型波长下无因次运动幅值随入射波幅增加的变化情况，数值和试验结果变化趋势总体上较为一致。可以发现包括船体砰击载荷的船舶运动幅值总体上比不考虑船体砰击载荷的结果要小，除了图12的垂荡运动幅值外，其他结果都显示考虑砰击载荷后船体垂向运动预报结果得到了很大改善。对于加入砰击力后船舶垂向运动计算结果减小的原因，可从以下两个角度分析：

由图9和图10可知，在=0.25顶浪规则波中，该船垂向共振运动位于波长船长比为1.0～1.5范围内。图12～14给出的非线性运动的入射波长落在共振波长范围内，此时船体特别是船首与波浪间具有较大的垂向相对运动，对应的外飘砰击载荷量级也较大、对整船流体载荷和运动影响也较大。

图10 顶浪规则波中一阶垂荡和纵摇运动幅值对比（Fr=0.25，HW/λ=1/40）

另一个原因是对于共振的船体运动，流体阻尼力对于减缓船体运动有较大作用。当前采用的砰击力模型与船波相对速度平方相关，可推断砰击力产生了某种阻尼效应，减缓了共振频率处的垂向运动幅值。

当前本文采用的砰击载荷模型没有考虑水面的上涌效应，KIM等采用了类似的VON KARMAN砰击载荷模型开展了船体的砰击力评估，他们指出如果沿着船体垂向剖面等效楔形体斜升角变化，该砰击载荷模型可能高估或者低估船体的砰击力，这一原因可能是导致当前本文的模型在某些波况下预报的船体运动效果不理想的原因。从图12来看，在波长船长比1.0情况下，当入射波陡＞0.02时，流函数理论得到的非线性垂荡幅值比线性波理论结果要大。从图13和图14来看，在入射波陡＞0.03时，两者不同的波浪理论模型得到的垂向运动幅值差别逐渐明显，特别是不考虑砰击载荷的船舶运动预报结果。垂向运动受波浪模型影响的原因与垂向F-K力相关，在本文下一节中，将结合更大范围不同入射波陡下的垂向波浪力与运动预报结果对这一问题再深入分析。

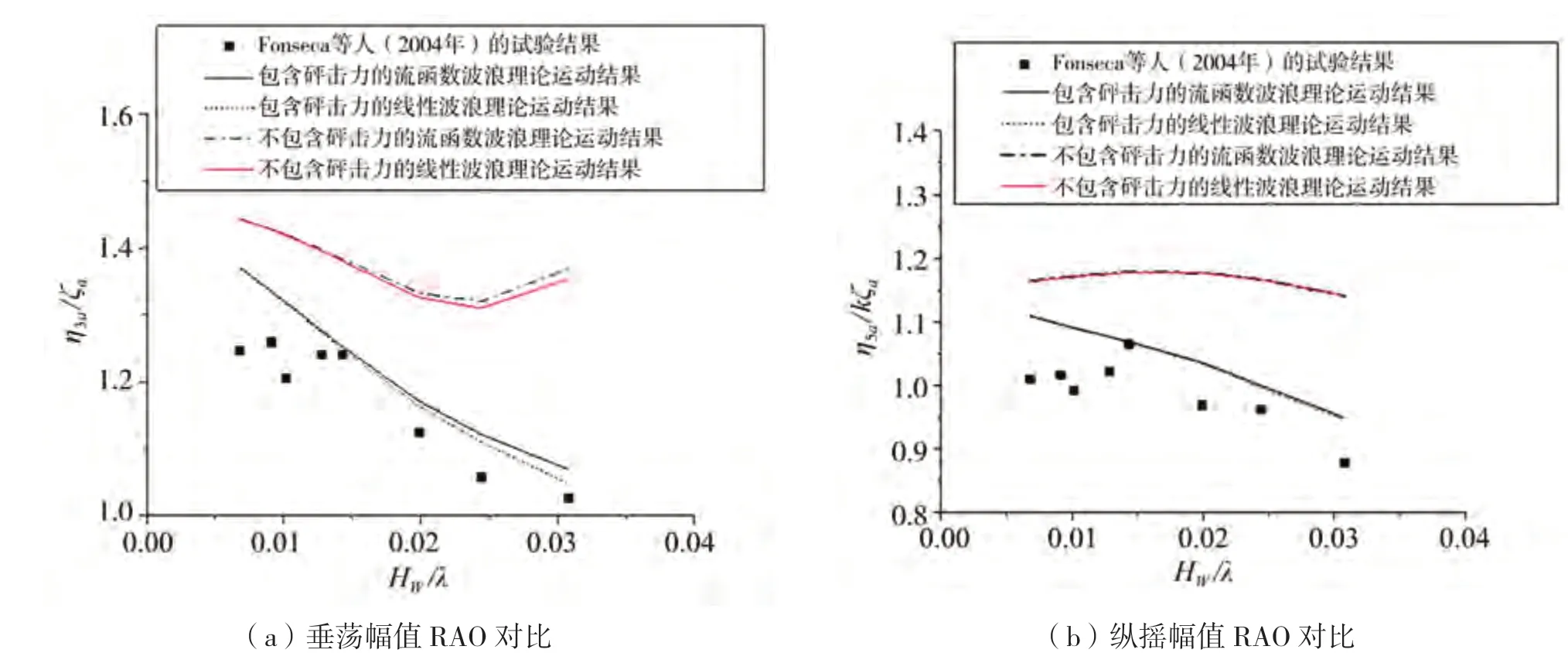
图13 顶浪中一阶垂荡和纵摇运动幅RAO对比（Fr=0.25，λ/Lpp=1.2）

图14 顶浪中一阶垂荡和纵摇运动幅值RAO对比（Fr=0.25，λ/Lpp=1.4）

在当前的弱非线性数值模型中，考虑了砰击载荷对运动的影响，这在一定程度上考虑了船体受到的非线性水动力载荷对船体的作用，从当前来看有助于改善船体总体运动的预报，发展更为精细的船体大幅运动的辐射与绕射水动力载荷预报模型应该会更为有助于进一步的船舶大幅运动预报精度。

2.2 不同波陡下非线性波浪模型对船体垂向 F-K力和运动的影响

图15至下页图17给出了3个不同波陡下相对于静水面的水下典型位置自由波面、入射波动压力对比。图中，水平轴采用波浪周期无因次化，波面起伏采用线性入射波幅无因次化，波浪压力采用ρgζ无因次化。式中：表示密度，kg/m；是重力加速度，m/s。

图15 小波陡情况下波面和入射波动压力对比（HW/λ=1/120，T=11.59 s，z=-6.5 m）

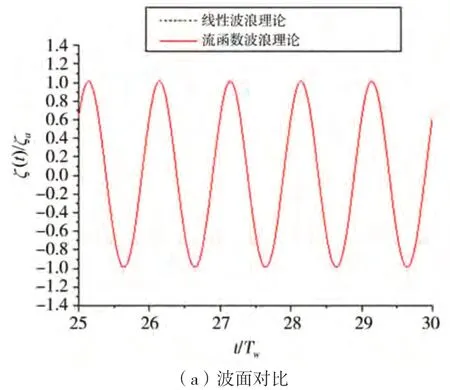
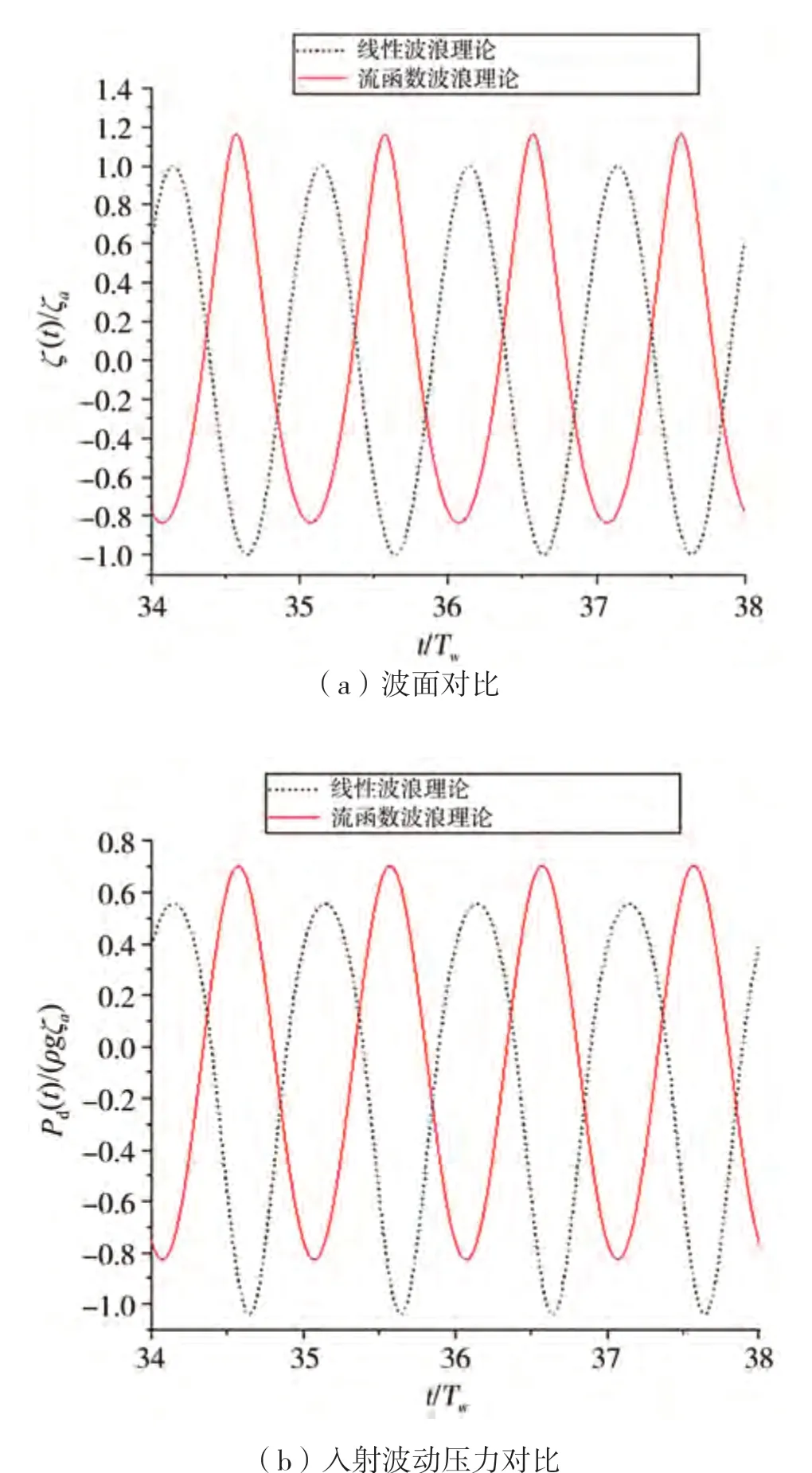
图17 波陡1∶10情况下波面和入射波动压力对比（HW/λ=1/10，T=11.59 s，z=-10 m）

图15中，入射波陡是1/120，对应的线性入射 波长为1.2倍船长，波浪非线性效应很小，线性波（LN）结果与流函数理论结果符合很好。图16中，入射波陡是1/20，流函数理论给出的波面起伏表现出显著的非线性特性，表现出尖峰坦谷的特征。对于入射波动压力，非线性波浪理论给出大的峰值压力和幅值偏小的谷值动压力。图17中，入射波陡是1/10，从中可以看出流函数理论得到的波面非线性更显著，波峰比波谷高45%。对于入射波动压力，流函数理论给出的峰值压力比线性波浪理论大30%，而谷值大小比线性波浪理论小24%左右。

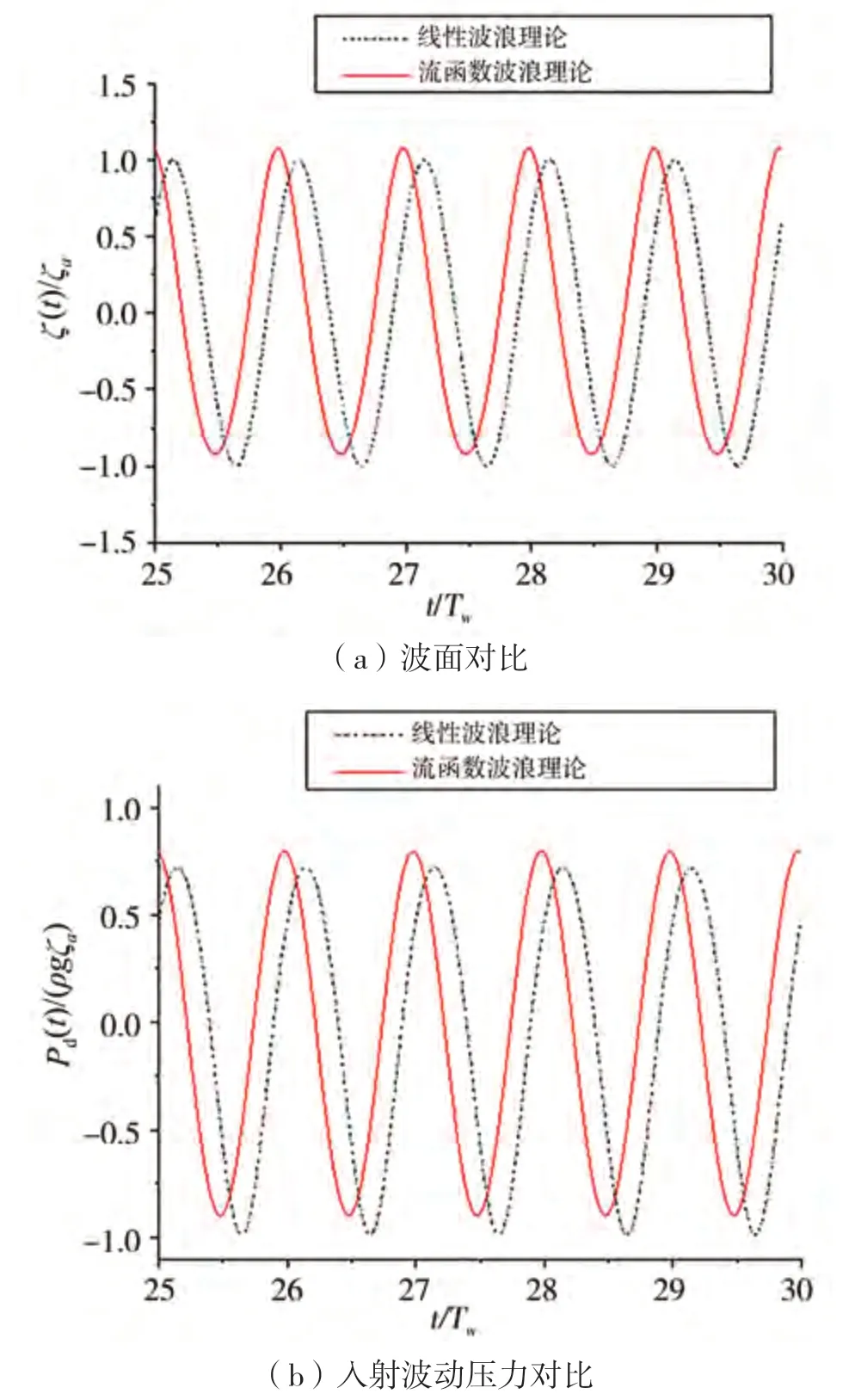
图16 波陡1∶20情况下波面和入射波动压力对比（HW/λ=1/20，T=11.59 s，z=-6.5 m）

图18至下页图20中给出了不同波陡下约束船体受到的垂向和纵摇方向的入射波主干扰力和静水压力的积分之和的对比，对于垂向力去除了平均浮力的贡献。公式中的垂向波浪力用Δgζ /L无因次化；而纵摇波浪力矩用Δgζ无因次化；Δ表示船舶排水量，kg；L表示垂线间长，m。

图18 S175集装箱船迎浪垂向F-K力和纵摇力矩对比（HW/λ=1/120，λ/Lpp=1.2，Fr=0）

图20 S175集装箱船迎浪垂向F-K力和纵摇力矩对比（Hw/λ=1/10，λ/Lpp=1.2，Fr=0）

图19 S175集装箱船迎浪垂向F-K力和纵摇力矩对比（Hw/λ=1/20，λ/Lpp=1.2，Fr=0）

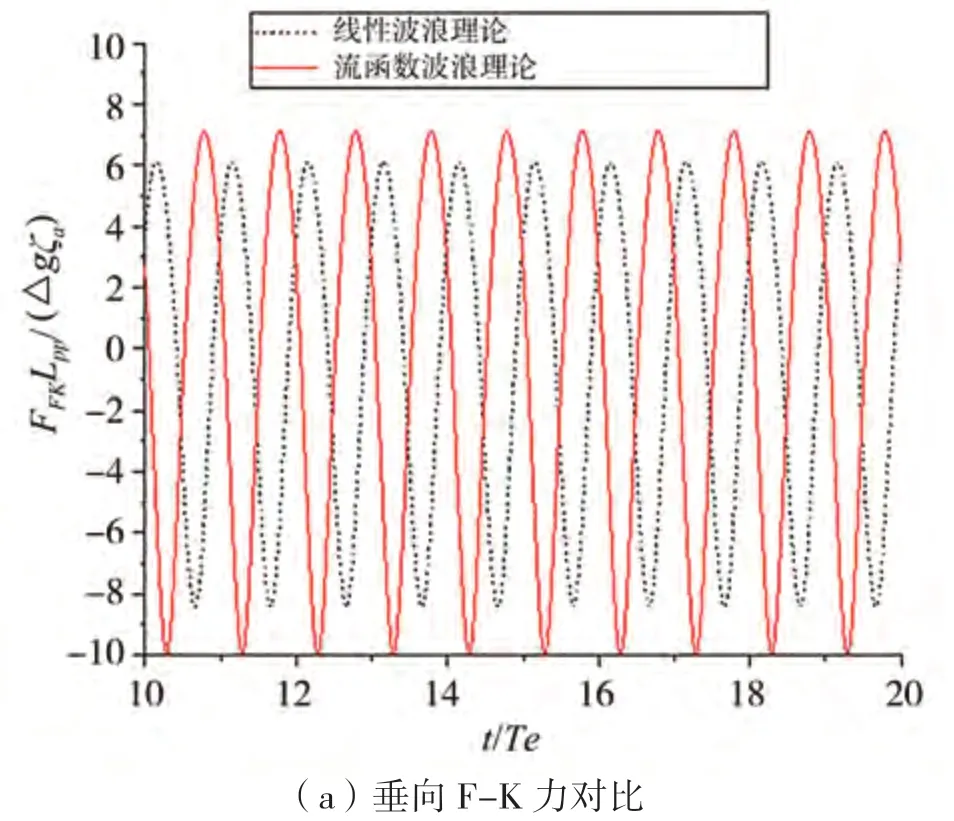
从图18～20看出，两种波浪模型结果在较大波陡1/20，1/10时具有较大差异，流函数理论给出的垂向波浪力的峰值比线性波浪理论的结果要大。两者之间的差异主要是由前面分析的波面起伏和入射波压力造成的。

下面分析了采用不同波浪模型下S175集装箱船垂向运动的对比，分析了入射波陡对结果的影响，波长船长比为1.2，取为0和0.25。为了单纯考虑波浪模型的影响，在船舶运动分析时没有考虑外飘砰击载荷对运动的影响。

下页图21给出了在时刻268.8 s空间波形的对比。在入射波陡为1/120时，两种波浪模型给出的结果较为一致；而在入射波陡为1/20时，流函数理论给出的波面峰谷值与线性波理论有差异，而且可以发现线性波浪理论得到的波长比流函数理论的波长略小一些，这是由于波浪色散关系的非线性效应造成的。

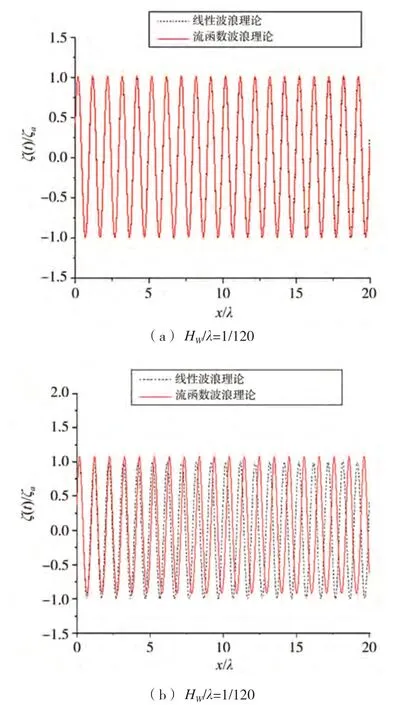
图21 不同波浪模型获得的波面起伏比较（λ/Lpp=1.2）

图22～23给出了波陡为1/20、1/10情况下的垂向运动时历对比，线性波浪理论与流函数波浪理论得到的结果有一定的相位差。该相位差产生原因与两种波浪理论模型给出的入射波长在大波陡时不一致有关，由此造成了船舶遭遇波浪周期由两种波浪模型给出的结果有一定差异。

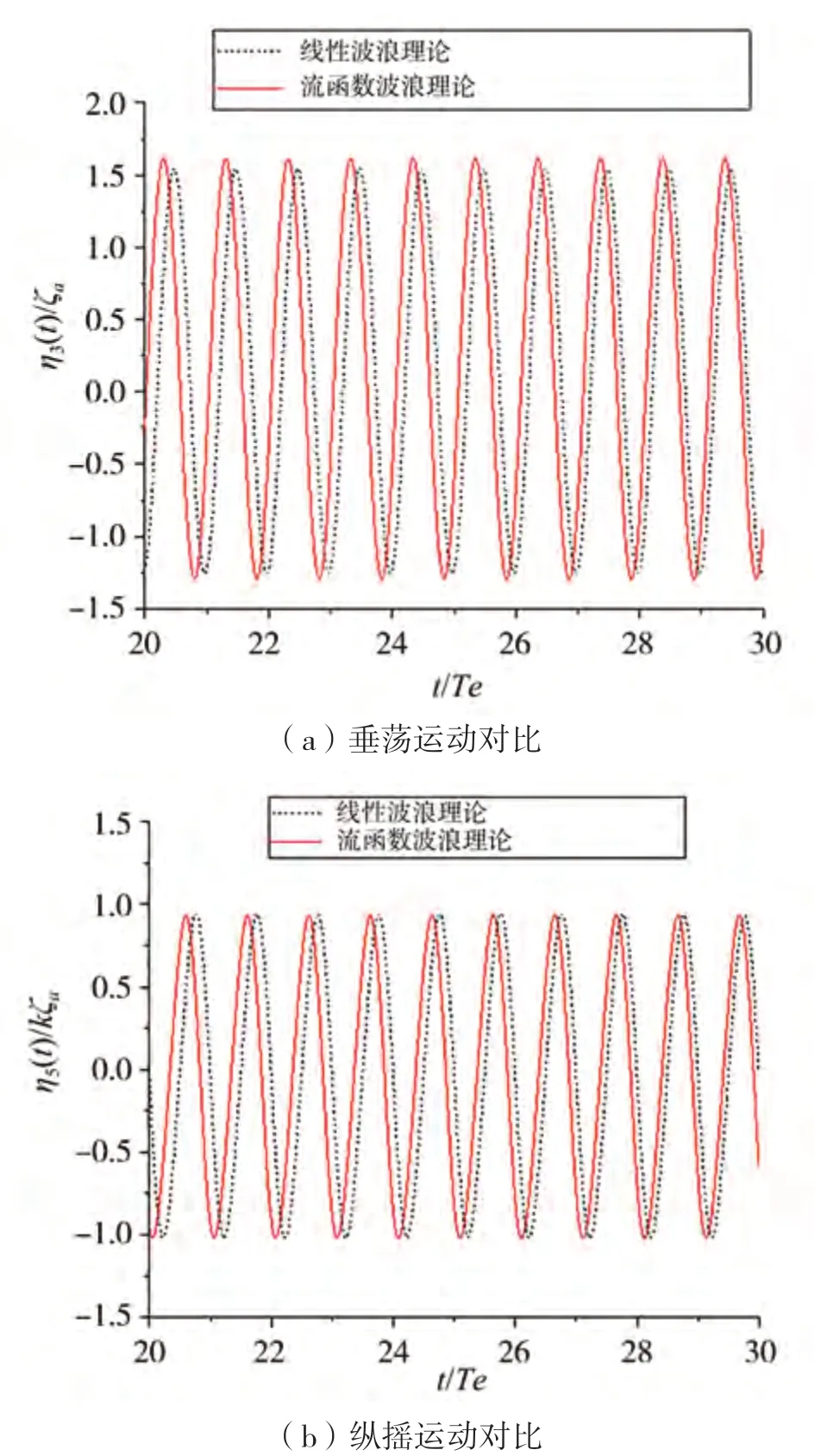
图22 不同波浪模型获得的迎浪规则波垂向运动比较（HW/λ=1/20，λ/Lpp=1.2，Fr=0.25）

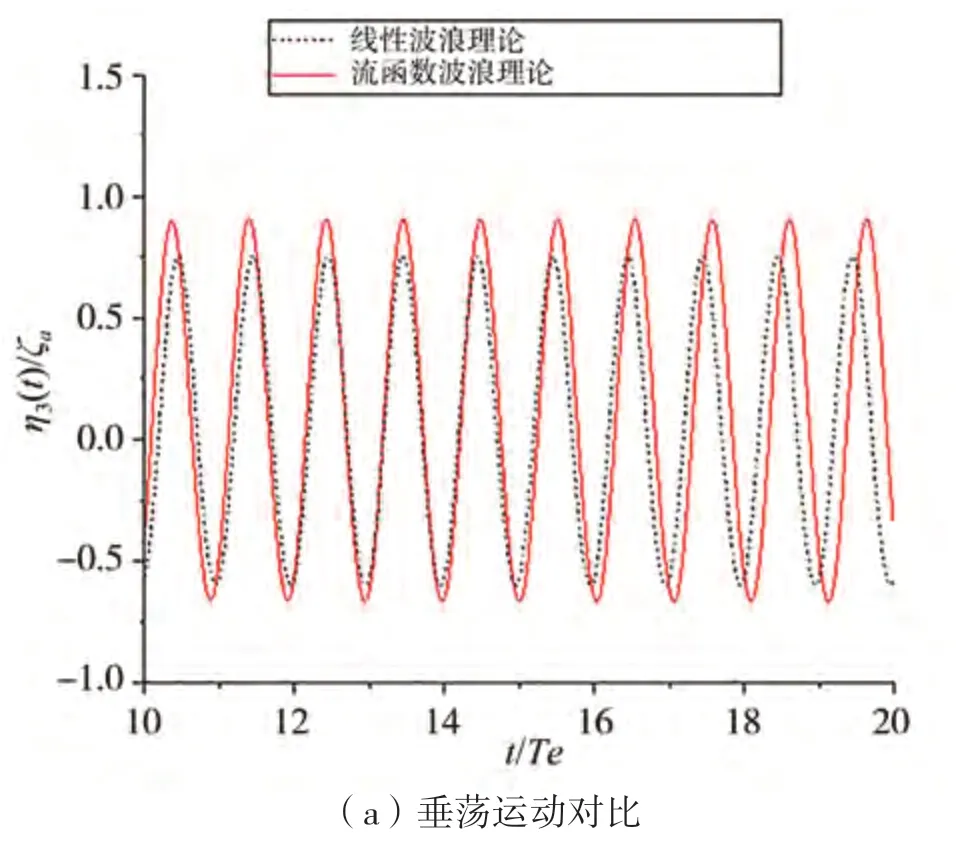
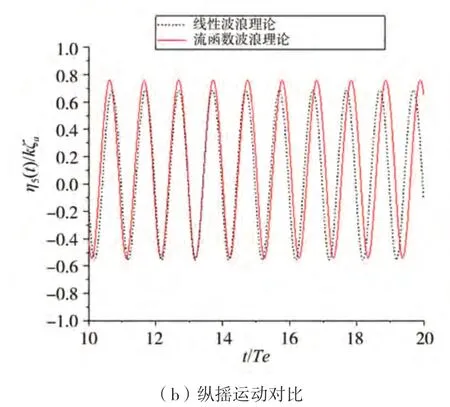
图23 不同波浪模型获得的迎浪规则波垂向运动比较（HW/λ=1/10，λ/Lpp=1.2，Fr=0.25）

下页图24～25给出了2种波浪模型下一阶运动幅值随着入射波陡变化结果，图24给出的是零航速结果。在波陡＜1/30时，两者较为一致；而当波陡＞1/30时，垂向运动幅值特别是垂荡运动幅值差异变得较为明显，流函数理论给出的结果要大于线性波模型结果。在为0.25时，在入射波陡＞1/30时，2种波浪模型间运动幅值也显示出差别，但差异比零航速要小。对于纵摇运动，2种波浪模型给出的结果较为一致，但零航速在波陡＞1/15时除外。通过前面分析可知，不同入射波陡下的船舶运动幅值差异主要是由2种波浪模型下波面起伏、波动压力作用下船体上的垂向波浪主干扰力引起的。

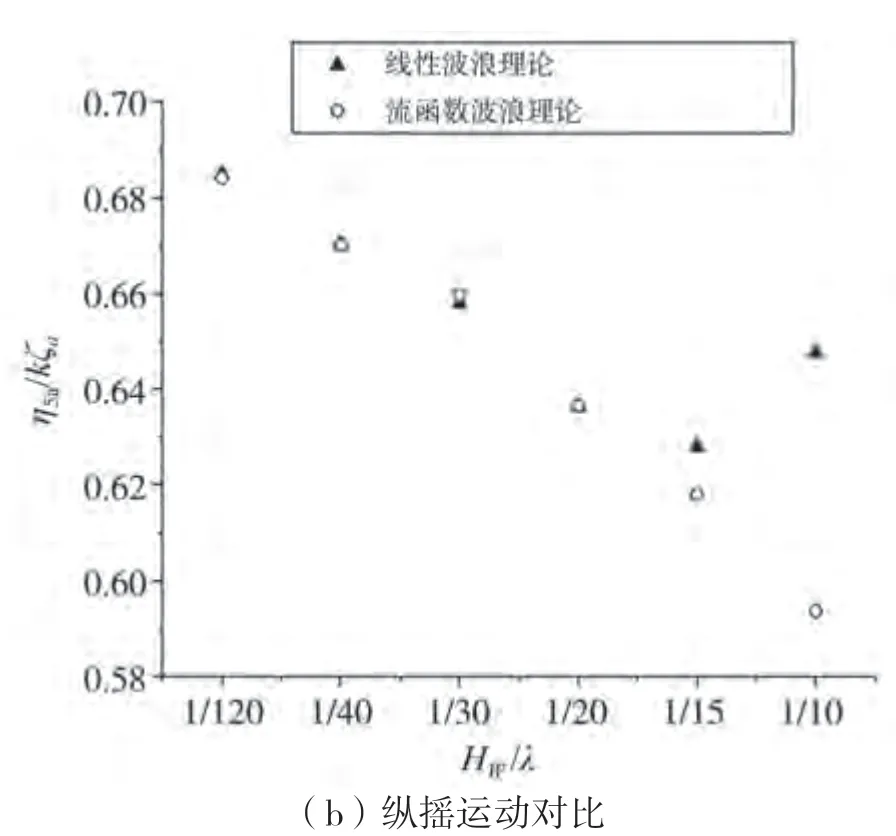
图24 不同波浪模型、不同波陡下顶浪规则波中垂向运动幅值（λ/Lpp=1.2，Fr=0）

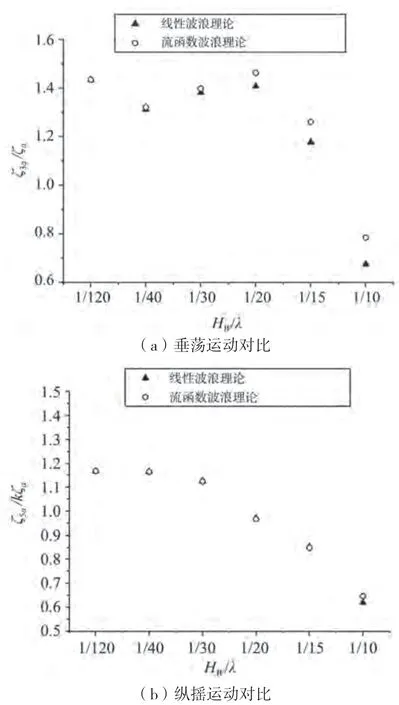
图25 不同波浪模型、不同波陡下顶浪规则波中垂向运动幅值比较（λ/Lpp=1.2，Fr=0.25）

3 结 论

本文介绍了一个求解垂荡和纵摇耦合运动的弱非线性数值模型，研究了全非线性流函数波浪理论的应用。在数值模型中，基于脉冲响应函数法的卷积积分计算了时域的辐射力和绕射力。利用瞬时湿表面上的压力积分估计了F-K力和流体静力恢复力。在动量冲击理论的基础上，考虑了外飘砰击力载荷。对S175集装箱船在规则波中的垂荡和纵摇运动进行了数值模拟，并与船模试验数据进行了比较。

可以得出以下结论：

（1）在相对较大的波陡1/20、1/10时，基于流函数波浪模型和线性波浪模型的F-K力和流体静力恢复力有明显差异。用流函数波浪模型计算的垂向F-K力比用线性波浪理论计算的要大。对应波陡下，基于流函数波浪理论的升沉运动结果也大于使用线性波浪理论的结果。就波浪模型对垂向运动的影响而言，尤其是在零航速情况下，当入射波陡度＞1/30时，垂荡运动表现出较明显的差异，而纵摇运动振幅在入射波陡度相对较大时对波浪模型不太敏感。

（2）通过计算船舶的外飘砰击力，在船型较大时（目前船型≈0.15～0.2），砰击力会影响船舶在共振运动附近的垂向运动。当波陡较大时，砰击力对船舶垂向运动的影响更为显著。考虑砰击力的船舶非线性响应幅值比不考虑砰击力的结果一般要小。

（3）通过与模型试验和CFD计算的比较，表明动量冲击理论一般能提供较好的砰击载荷精度。在大多数情况下，现有的动量冲击砰击模型的应用有助于改进船舶垂向运动的数值预报，它在一定程度上反映了非线性水动力的贡献。为了更好地模拟船舶在恶劣海况下的非线性运动，需建立更精确的非线性辐射力、绕射力和砰击力模型。

（4）本文主要研究全非线性波浪模型对规则波中垂向运动的影响，在不规则波中的影响将更加复杂和重要，未来的研究应朝着这个方向进行。