基于改进能量包线随机平均法求解窄带谱激励下船舶随机参激横摇响应

刘亚柳 刘利琴 刘依伦

（天津大学 水利工程仿真与安全国家重点实验室 天津 300072）

0 引 言

船舶在遭遇恶劣海况时，为了避免横风横浪的影响，通常会调整航向，选择纵浪或斜浪航行。但即使船舶在静水中有足够的稳性，在纵浪和斜浪航行时，仍有发生大角度摇摆乃至倾覆的可能。随着船-波相对位置的周期性变化，船舶横摇复原力矩也呈现出周期性变化，从而引发显著的参数横摇运动。国际海事组织（IMO）制定的第二代完整稳性衡准包含了参数激励横摇等5种失效模式，更加深入地研究了船舶在波浪中的动稳性问题。

随机波浪中的船舶大幅横摇运动非常复杂。首先，它是一个强非线性问题，包括了以下非线性项：非线性恢复力、非线性阻尼力和非线性波浪载荷。其次，由于海浪的随机特性，船舶运动响应为随机过程。因此，本文研究的随机波浪中船舶横摇运动是一个强非线性随机动力学问题，不能用确定性方法描述，也不能采用常规的谱分析方法。研究随机波浪中船舶横摇运动响应和稳性最直接的方法是数值模拟，许多学者基于数值模拟对参数横摇问题进行了大量研究。ESPARZA等采用安全池理论衡量了船舶在参数激励下的抗倾覆能力，并分析了安全池形状面积随环境参数的变化以及破损现象。SILVA等基于切片理论提出了研究迎浪船舶动稳性的新方法，并将该方法拓展到船舶六自由度非线性运动模型，通过与试验结果对比，验证了该方法的可行性。MATSUDA等考虑横摇恢复力矩的变化研究了规则和随机纵浪和斜浪中船舶的参数激励横摇运动，其中横摇恢复力矩系数根据模型实验测出。BELENKY等对顶浪中C11型集装箱的参数横摇运动进行了数值模拟，并采用统计方法和傅里叶变化得到了响应谱密度和自相关函数。

船舶倾覆是十分罕见的事故，因此解析方法对于评估船舶倾覆概率，衡量船舶横摇稳定性仍然十分必要。在应用随机平均法求解随机响应时，一般要求随机激励的功率谱为宽带谱。朱位秋指出，随机平均法的基本思想是将随机运动响应近似为扩散的马尔可夫过程。随机平均法的准确性在很大程度上取决于激励谱带宽与响应谱带宽的比值。但在实际工程应用中，系统的实际响应带宽并不是很大，因此也可以采用随机平均法求解非白噪声激励下的响应。ROBERTS采用随机平均法求解了有色噪声激励下的横摇运动方程，基于Fokker-Planck方程推导出了横摇稳态响应的概率分布。然而，这种随机平均方法仅能反映系统的非线性阻尼特性。当船舶具有强非线性恢复力时，该方法在大横摇角处表现出明显的误差。另一方面，MARUYAMA等采用能量包线随机平均法借助Hamiltonia量则可以同时考虑非线性阻尼和非线性恢复力。DOSTAL等采用能量包线随机平均法求解了以RORO船的横摇稳态概率密度函数。柴威等采用能量包线随机平均法和路径积分法研究了随机海浪中船舶非线性横摇运动响应。研究表明：随机平均法的基本思想是对原始系统进行降维处理，从而降低随机响应的计算难度；相比之下，路径积分法则是基于系统的马尔可夫性质，在时间域内求解相应的Fokker-Planck方程，得到随时间演变的船舶横摇运动的转移概率密度。

虽然有一些学者成功采用能量包线随机平均法求解了某些特定船舶的横摇运动响应，但本文作者以C11型集装箱船为例，研究高海况下的船舶横摇运动响应时，采用能量包线随机平均法得到的结果与数值模拟的结果有明显差异。MARUYAMA等采用该方法求解ITTC A1型集装箱船的横摇运动响应时也出现了类似现象。本课题组研究了外部激励强度、激励带宽和系统阻尼对能量包线随机平均法计算精度的影响，给出了该方法求解窄带海浪激励下船舶横摇运动的适用性条件。当采用能量包线随机平均法求解非白噪声激励的系统响应时，要求系统的阻尼和外部激励强度足够小且激励带宽足够大。如果不满足这些条件，则需要采用数值方法来计算横摇响应，以获得更准确的结果。随机平均法分为标准随机平均法和能量包线随机平均法。标准随机平均法虽然应用很广泛但在平均过程中会损失掉非线性恢复力项从而不能计及其对响应的影响。而能量包线随机平均法虽然能弥补标准随机平均法的这个缺陷，但一般要求外界激励为理想白噪声。船舶与海洋工程结构物遭遇的实际海浪一般具有有限的带宽以及给定的谱密度函数。当外界激励为窄带谱，并采用非线性阻尼和非线性恢复力描述船舶横摇运动方程时，2种随机平均法的适用性范围受到限制。

本文基于这个背景，通过改进能量包线随机平均法求解非线性横摇系统在窄带随机波浪激励下的响应。以C11型集装箱船为例，考虑非线性阻尼力和非线性恢复力建立横摇单自由度运动方程，分析其在随机波浪下的运动响应特性。采用BULIAN提出的改进Grim有效波理论来描述随机波面升高以降低解析方法的求解难度，即用固定波长的规则波在一个船长范围内对不规则波波面进行最小二乘替换，将波幅和船波相对位置作为随机过程。假设船舶在波浪中的运动为准静态过程，基于切片理论数值计算横摇复原力矩，并采用解析表达式进行拟合。采用改进能量包线随机平均法求解随机激励下船舶的横摇运动响应，得到横摇角的概率分布，更直观地展示船舶的稳性特征。采用蒙特卡洛法数值计算横摇响应分布，验证改进能量包线随机平均法的准确性。

1 参数激励横摇运动方程

式中：为横摇角，rad；I为横摇惯性矩，kg·m；A(ω)为横摇附加惯性矩，kg·m；ω为横摇固有频率，rad/s；为线性阻尼系数，N·m·s；为立方非线性阻尼系数，N·m·s；Δ为排水量，kg；为重力加速度，m/s；(，，)为船舶复原力臂，m，由()、()和()决定，其中()为波幅，m，()∈［0，2π］为船和波的相对位置，rad；为时间，s。

本文采用Grim有效波理论描述随机波面升高，因此整个船长范围内随机波面，可以用波长等于船长的规则波进行拟合。在波长等于船长的规则波中，基于切片理论和Froude-Krylov假设数值计算不同、和时C11集装箱船的复原力臂函数(，，)。采用高斯积分求解作用在船体上的流体力，考虑瞬时湿表面计算静水恢复力和F-K力。复原力求解示意图如图1所示，船舶横摇复原力矩为：

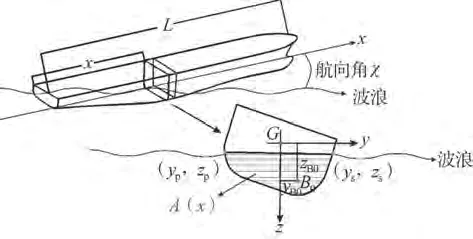
图1 复原力臂计算示意图

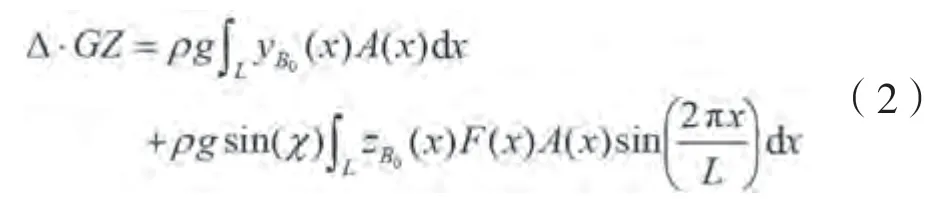
式中：为海水密度，kg/m；为船长，m；y()与z()为各浸水横剖面形心在参考坐标系下的坐标，m，参考坐标系以船舶重心为原点，不随船的运动而旋转。()为各浸水横剖面面积，m；为航向角，°；()为各横剖面的压力梯度系数。

为了使用解析方法求解运动方程（1），将(，，)展开为关于横摇角的多项式：

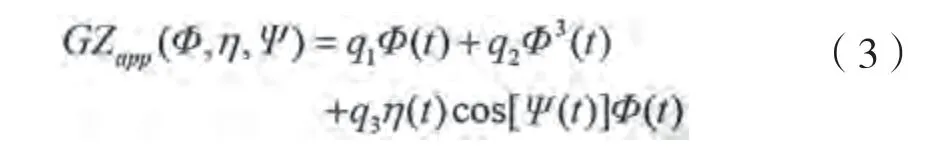
式中：q (1，2，3)为展开项的系数，使用最小二乘法确定。

采用JONSWAP波浪谱对随机海况进行描述：

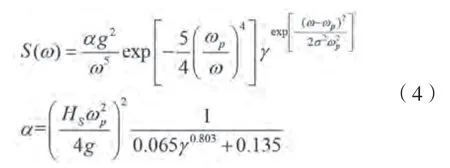
式中：为能量尺度度量；为谱峰升高因子；ω为谱峰频率，rad/s，ω=2π/T，T为谱峰周期，s；H为有义波高，m；为峰形参数。当波浪频率ω＜ω时，0.07；当ω＞ω时，0.09。

图2是根据有义波高和谱峰周期的联合概率密度绘制的波浪散布图。它表示100 000次海浪观测中不同有义波高和谱峰周期组合的数量。

图2 波浪散布图

本文以C11型集装箱船为例，采用改进能量包线随机平均法求解其在随机波浪中的横摇运动响应。C11型集装箱船的主尺度参数如表1所示。

表1 C11型集装箱船主尺度

2 改进能量包线随机平均法

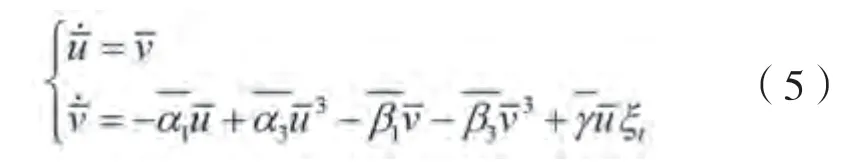
式中：

并作如下尺度变化：

为了书写简便，以下用替代，则运动微分方程（5）变为：

系统总能量的具体表达式为：

基于原始能量包线随机平均法计算不同海况下的横摇角概率分布，并与蒙特卡洛数值模拟得到的结果进行对比。采用Kullback-Leibler（KL）散度描述能量包线随机平均法的横摇角度概率分布于蒙特卡罗法计算结果的差异。如果2个分布相同，KL散度为0。当2个分布之间的差异增加时，KL散度也会增加。

从图3可以直观地看出，随着有义波高和峰值因子的增大，原始能量包线随机平均法计算的准确性降低。因此，采用原始能量包线随机平均法计算高海况下船舶横摇运动响应时，存在很大误差，严重影响横摇稳性评估。

图3 不同海况下的KL散度

基于以上背景，对原始能量包线随机平均法进行改进。借鉴标准随机平均法引入相角，进行坐标变换：

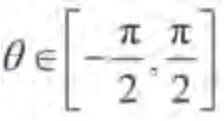
公式（8）两边对时间求导可得：

公式（7）下式的左右两边同时乘以可得：

联立公式（10）和公式（11）可得：

由公式（9）可知：

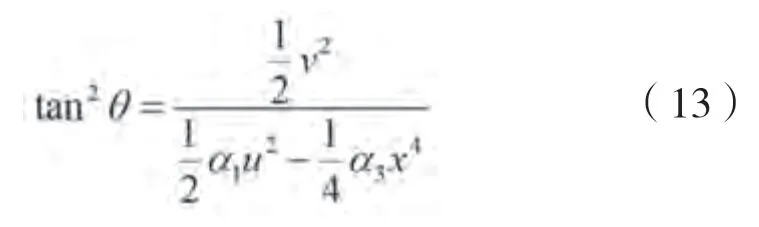
则：

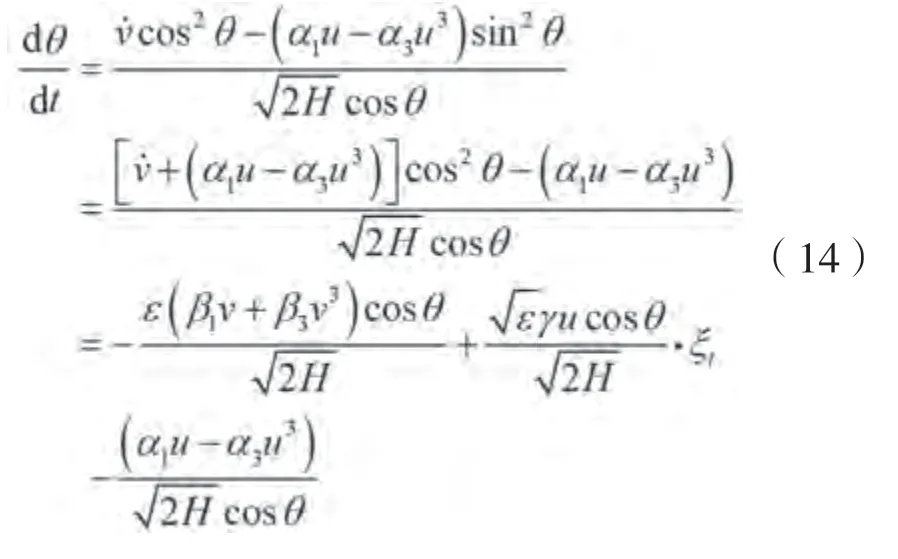
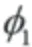
根据公式（9）可以将、表示为和的函数，代入公式（12）和公式（16）中可以得到标准形式的随机微分方程为：

式中：

式中：()为ξ的自相关函数；

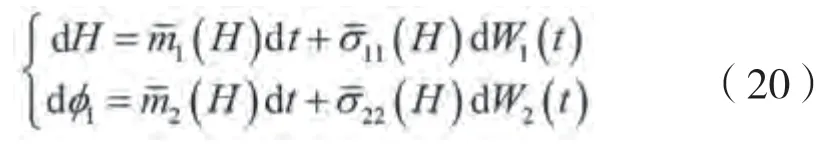
式中：()和()为相互独立的维纳过程。

对于上述的平均伊藤随机微分方程（20），其响应为扩散过程，系统能量对应的转移概率密度(，，)满足如下的FPK方程：

在船舶不发生倾覆的前提下，式（21）对应的平稳概率密度函数为：

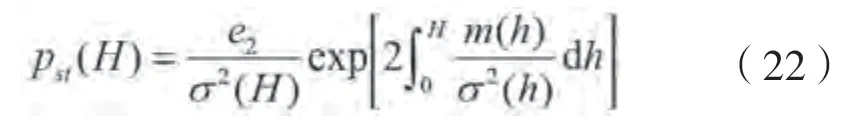
式中：参数由边界条件确定。

根据能量的平稳概率密度函数，可以很容易地得到横摇角和横摇角速度的联合概率密度函数。其对应的解析表达式为：

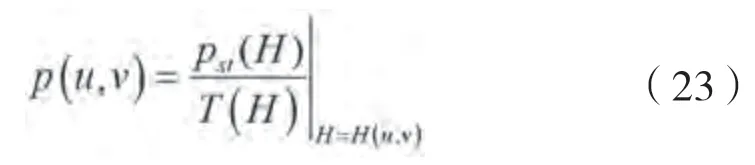
对横摇角速度进行积分，进而得到横摇角的概率密度分布。

打底层为了避免熔池在正面焊缝产生坠瘤，坡口两侧熔合良好，焊接过程中焊条向坡口根部用力送进，并在坡口两侧稍许停留，以保证背面的穿透和坡口两侧的熔合性。由于焊条电弧焊时焊条的电阻大、焊条易发红，后半部分焊条的使用性能较差，所以在焊接过程中应留有稍长的焊条头，以5cm为宜，避免出现焊条沾粘、保护不良等焊接缺陷。

3 计算结果分析

本文重点研究高海况下采用改进能量包线随机平均法预报船舶大幅非线性横摇运动。因此，选取海况使船舶遭遇谱的谱峰频率在横摇固有频率的2倍附近，以激发参数激励横摇运动。采用JONSWAP波浪谱对随机海况进行描述，=1。船舶在随机波浪中顶浪航行，具体计算工况如表2所示。

表2 计算工况

随船坐标系下遭遇频率ω的表达式为：

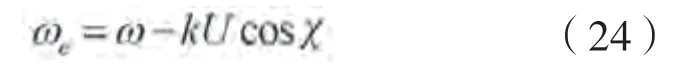
式中：为波数；为航速，kn。

遭遇频率ω下的海浪谱(ω)的表达式为：

采用四阶龙格库塔方法对方程（5）进行数值计算，并采用蒙特卡洛法统计横摇角的概率分布，随机参数激励下的横摇角具有普遍非各态历经性。为了克服这一现象，需要在同一海浪谱下进行多次不同的实现。因此，选取 500个随机种子数，每次数值模拟的时长为50 000 s。将解析方法得到的横摇角概率密度分布与蒙特卡洛法得到的结果进行比较以验证改进能量包线随机平均法的准确性。

不同工况下原始和改进能量包线随机平均法的计算结果以及和蒙特卡洛法的对比如图4至图7所示。

图4 工况1计算结果

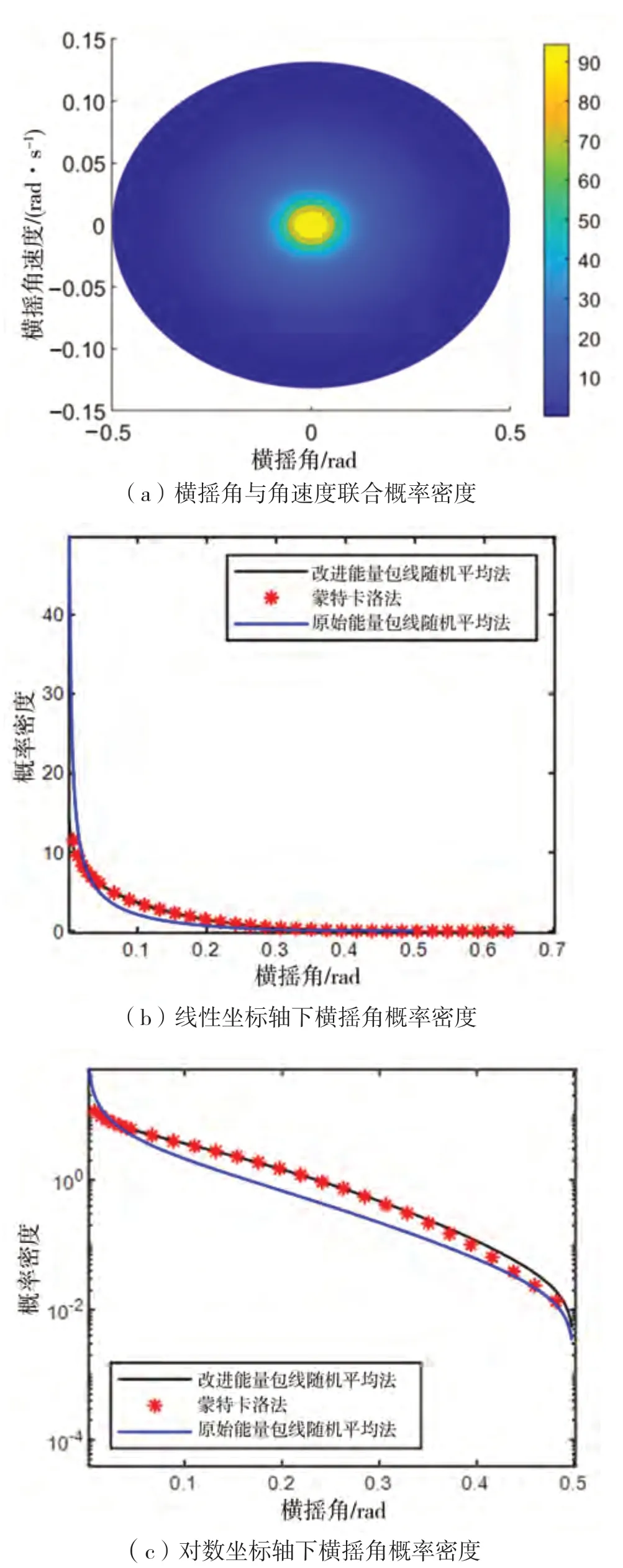
图7 工况4计算结果

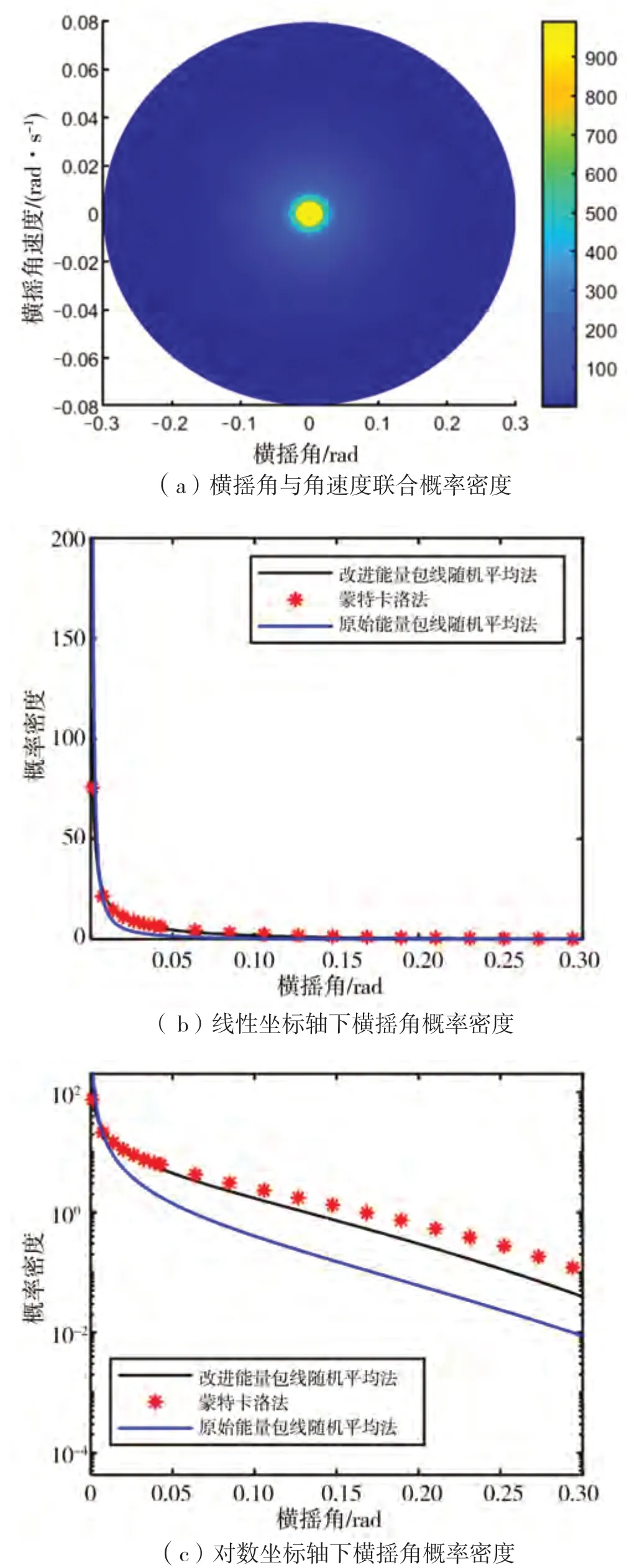
图5 工况2计算结果

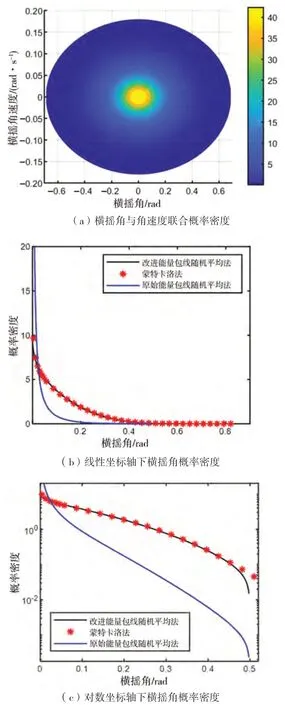
图6 工况3计算结果

由图4至图7的计算结果可知，改进能量包线随机平均法能够大幅提升随机平均法的准确度，计算高海况下船舶参数激励横摇运动响应分布，对船舶稳性进行直接评估。但是从对数坐标轴中能够看出，横摇角概率密度曲线在尾部区域仍存在一定的计算误差。

4 结 语

本文提出改进能量包线随机平均法，在原有的能量包线随机平均法的基础上借鉴标准随机平均法引入相角。将非线性系统对随机激励的响应近似看成扩散的马尔柯夫过程，推导能量与相角满足的伊藤随机微分方程，将漂移系数和扩散系数在快变量的一个周期内进行平均，得到支配系统能量的转移概率密度所满足的FPK方程，其中快变量对慢变量的影响由于其随时间迅速变化的性质被平均掉。改进的能量包线随机平均法既可以考虑非线性恢复力，又同时放宽了外部激励带宽的限制，使其可以为窄带随机激励。最后通过求解平均后的 FPK方程得到横摇角稳态响应概率分布。

改进能量包线随机平均法能大幅提升随机平均法的计算精度，在高海况下计算得到的横摇运动响应分布与蒙特卡洛法对比良好。但是从对数坐标轴中能够看出，横摇角概率密度曲线的尾部区域仍存在一定的计算误差。由于大横摇角区域对于准确预报船舶横摇倾覆概率或者首次穿越时间非常重要，因此后续仍然需要研究如何提高尾部区域预报的准确性。