船舶非线性动力学分析方法及工程应用

唐友刚 王丽元 刘 峥 刘利琴 李 焱

（1. 天津大学 建筑工程学院 天津 300350； 2. 江苏科技大学 海洋装备研究院 镇江 212003）

0 引 言

针对船舶二代稳性中的失效模式，目前主要的研究方法和手段有非线性动力学方法、模型试验方法和数值计算分析方法等。研究内容主要包括各种失效模式的发生机理以及如何避免船舶发生失稳。非线性动力学在研究船舶二代稳性中，有着不可替代的作用，是研究船舶失稳机理的主要手段。本文基于作者所在团队多年科研工作，总结船舶非线性动力学分析方法在船舶参数横摇、骑浪横甩方面的工程应用，探讨船舶非线性运动响应和稳性的研究方法，揭示船舶大幅运动响应、运动失稳直至倾覆全过程的非线性动力特性。

1 船舶参数横摇非线性分析

1.1 规则波中非线性响应

规则纵浪中船舶参数激励非线性横摇方程为：

采用多尺度法求解上述方程，得到近似解析解。当φ = 0时，得到方程的平凡解；但当参数激励的幅值、频率满足一定的条件时，将得到方程的非平凡解，横摇就会被激起。在参数空间内确定平凡解的稳定域与非稳定域，也就确定了参数激励横摇发生的条件。

由图1可见，当=0.4时，若遭遇频率与横摇固有频率的比值Ω从0开始增加，对于主参数共振来讲，渔政船的稳定横摇幅值将在T处发生跳跃，出现大幅横摇。继续增加Ω，横摇幅值逐渐变小，在T之后周期解失稳，平凡解稳定。

图1 渔政船幅频曲线h0=0.4

由图2可见，当=0.9时，若Ω从1.5开始增加，则船舶将在T处倾覆，平凡解失稳，而没有稳定的周期解。

图2 渔政船幅频曲线h0=0.9

1.2 非规则波中非线性响应

船舶在随机斜浪中航行，假设船舶的纵向运动为小量，得到船舶参-强激励单自由度横摇运动方程如下：

式中：为横摇角，rad；I为横摇惯性矩，kg·m；A()为横摇附加惯性矩，kg · m；为线性阻尼系数，N· m· s；为立方阻尼系数，N· m· s； Δ为排水量，kg；为重力加速度，m/s；为船舶复原力臂，m，由、和决定；()为波浪力矩，N·m。

采用能量包线随机平均法研究船舶随机参-强激励横摇运动概率密度函数。将船舶运动过程处理为马尔可夫过程，将运动响应分成快变量与慢变量，通过对快变量的平均得到慢变量的近似方程。

将随机波面升高处理为窄带随机过程，即用有效波面Z (，)来代替随机波面(，)。将Z (，)展开为2个随机过程η()和η()的组合，具体如下：

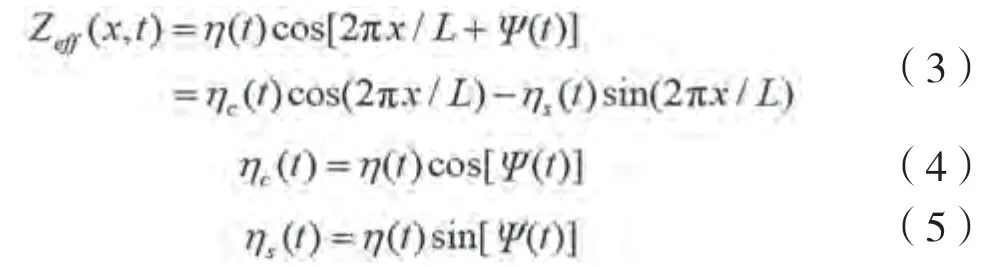
式中：η()和η()均为高斯平稳随机过程，经证明两者相互独立。

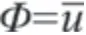
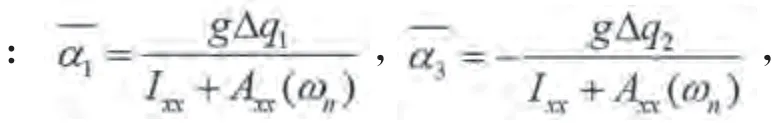
作尺度变换如下：

用替代t ，则运动微分方程为：

将响应分量分为快变量和慢变量，即系统的状态空间由（，）变换为（，），其中为系统总能量：

式中：每个能量值（，）对应于特定的横摇运动。例如：当=23.73、=19.74 时，得到对应的能量等值线，如图3所示。

图3 能量等值线

运动方程进一步写为：

引入中间变量（，），令：

则（11）可进一步写为如下随机微分方程式：

根据随机平均法，其漂移与扩散系数分别为：

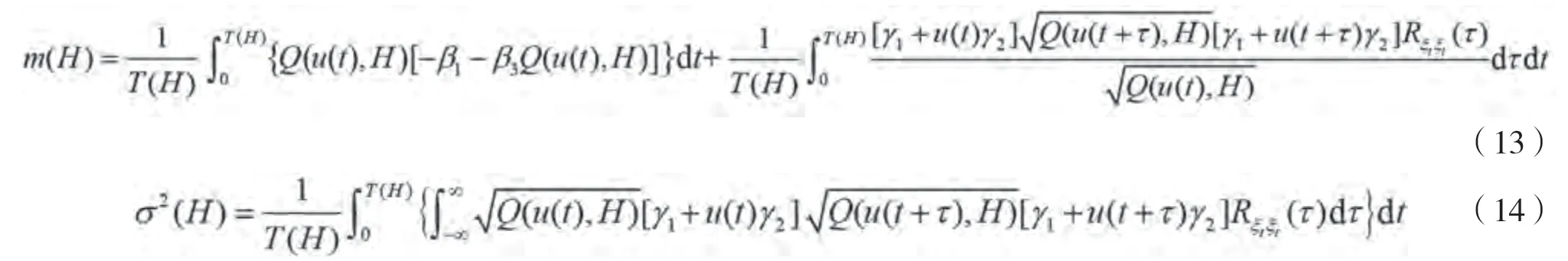
式（13）与式（14）中，（）为时间区间：

针对0≤≤H，采用雅可比椭圆函数求解运动微分方程，得到：

式中：、、为雅克比椭圆函数。符号定义为：

将式（15）至（18）代入式（13）与式（14），并考虑上述的符号定义，得到漂移与扩散系数为：

系统能量满足如下伊藤随机微分方程：

式中：（，）表示初始状态，该式可表达为式（23）所示形式：

引入尺度函数()与速度函数()：

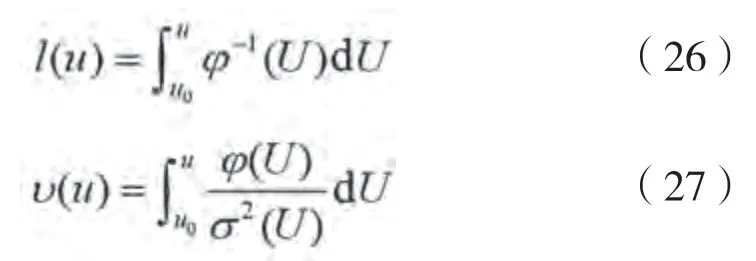
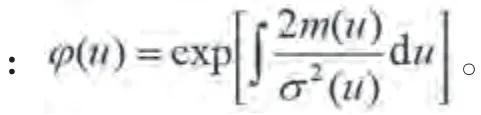
式（25）可进一步写为：

如果系统能量＞H，方程（28）不存在稳定解；如果≤H，则式（28）的平稳概率密度函数为：

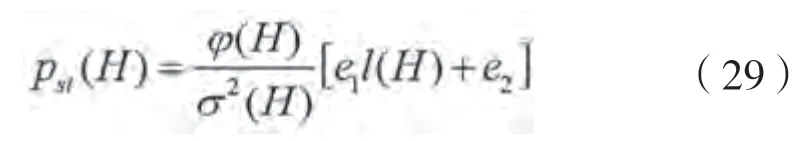
式中：参数、由边界条件确定。

对于低强度噪声激励有=0，则式（29）可进一步写为：

应用传递函数关系p()=p()(d/d)，得到基于变量的平稳概率密度函数为：

对式（30）在某一角度范围[，]内积分，可进一步得到()在该范围内的概率。

应用蒙特卡罗方法求解C11型集装箱船在实尺度下的横摇响应概率密度函数。随机种子数=25、迭代步数=5 000 000、时间步长Δ=0.01 s，得到的概率密度函数的数值解，其与随机平均法得到的结果对比如下页图4所示。对比结果表明，两者吻合较好，同时也证实本文采用的解析解法和数值解法的正确性。

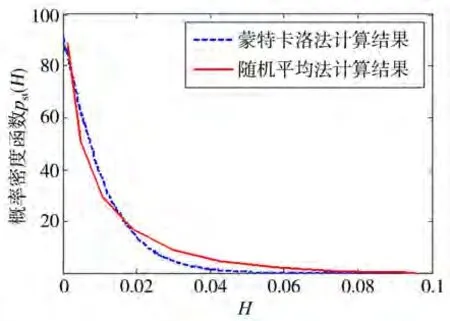
图4 概率密度函数对比

1.3 波群分析方法

波浪频谱不能反映波群的特性，本文用波包来描述波群，用波包谱作为靶谱来模拟相位谱，波包谱S()的靶谱：

同时，当≤0.7，f / f=5~15，当＞0.7，f / f=10~28。

采用波包谱数值模拟不规则波的波群过程如图5所示。

图5 波群模拟流程图

JONSWAP公式如下所示：

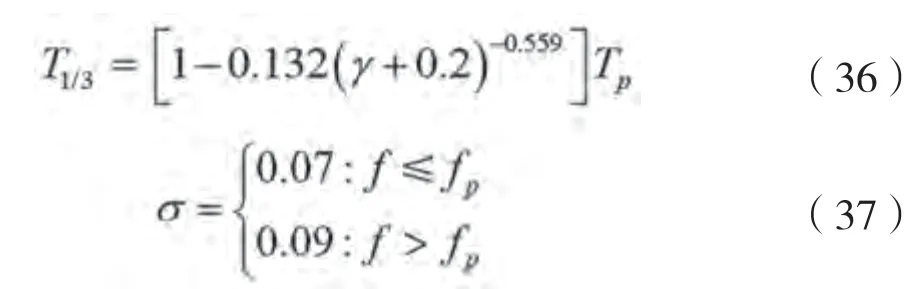
GFH和GLF分别表征波群的高度和长度特征， 参见图6。对于给定的频谱，当GFH不变，随着 GLF增大，波包靶谱面积基本不变，峰频减小，波包变平坦，群长增大；当GLF不变，随着GFH增大，峰频不变，波包谱面积增大，波包线的波动幅度增大，群高有明显变化。群高和群长对参数横摇有明显影响，群长的影响更显著。

图6 波群波面升高及船舶横摇角（GFH=0.8，GLF=9.82）

2 船舶骑浪运动非线性分析

参照图7坐标系，船舶在波浪中纵荡运动方程为：

图7 运动坐标系

式中：为船舶的质量，kg；m为纵荡附加质量，kg；ξ为船舶重心的纵坐标，m；()为船舶阻力，N；为纵向瞬时速度，m/s；(，)为船舶螺旋 桨推力，N；为螺旋桨转速，r/s；F(ξ，)为船 舶在纵向受到的波浪力，N。

船舶静水阻力()为：

式中：、、为多项式的系数。

船舶静水中螺旋桨推力（，）为：

式中：t表示为推力减额分数；为海水密度，kg/m；为转速，r/s；D为直径，m；K为推力系数。

基于切片理论，船舶在波浪中运动时受到的波浪力可表达为：

式中：为绕射效应修正系数；C为方形系数；C为中横剖面系数；为海水密度，kg/m；为重力加速度，m/s；为波浪幅值，m；为波浪的波数，m；为船舶航向角，rad；为船舶每站横剖面的湿面积，m；为每站的吃水，m；d为每站间隔距离，m；为每站的船体宽度，m。

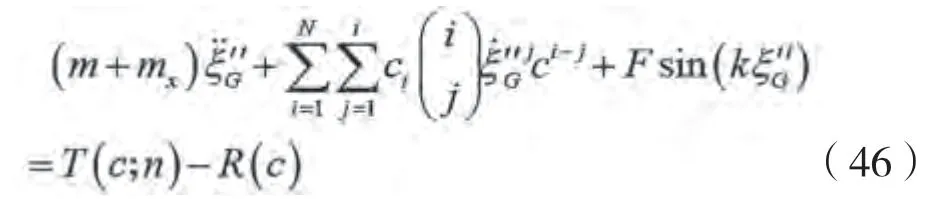
式中：c可用多项式表达如下：

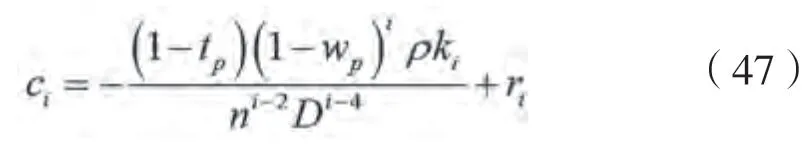
在方程（48）中引入小参数，其中0＜1，将纵荡方程（48）转为：

2.1 规则波中骑浪运动分岔研究

当小参数0时，式（50）退化为无阻尼和外激励作用的哈密顿系统：

将式（52）中的右端项取不定积分，并由第1项减去第2项，则得到方程（52）对应哈密顿的量（，）：

当哈密顿的量（+π，0）=1时，系统轨道如图8所示。

图8 异宿轨道示意图

其中，红色线为系统的异宿轨道线，红色线内部的蓝线则是表示系统的同宿轨道线。整个哈密顿系统存在着连接（π，0）和（-π，0）2个鞍点的 2条异宿轨道，在异宿轨道之间，存在着几条围绕着 （0，0）中心的同宿轨道。同宿轨道与异宿轨道的分界线，即为船舶纵荡运动中发生骑浪现象的分界线。系统的异宿轨道方程为：

忽略式（50）右端项中的小参数，将其沿异宿轨道积分，得到船舶纵荡运动方程的梅林可夫函数：

沿着（54）所示的异宿轨道进行积分，并使=0，则有：

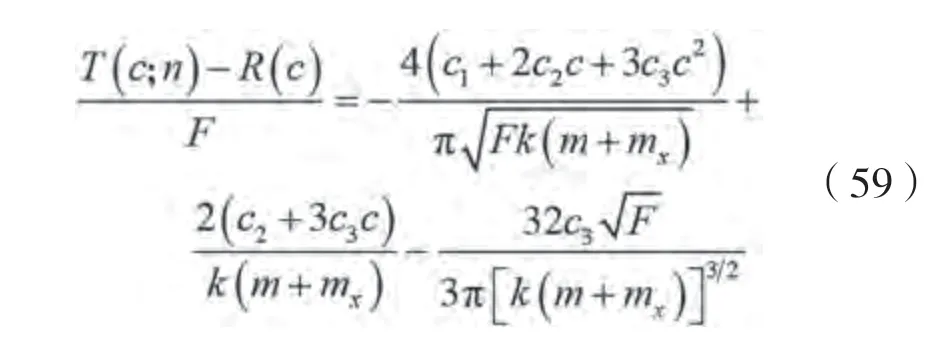
式（59）当中除了参数未知，所有其他参数都是已知的，所以根据式（59）可求出临界螺旋桨转速；再根据船舶在波浪中前行时的阻力和推力相等，求出船舶的临界船速，确定船舶骑浪失稳的条件。

以某内倾船为例开展研究，其主尺度如表1所示，推力系数和阻力系数由模型试验得到。分别采用解析方法和数值方法判断该船是否发生骑浪运动，给出对应的临界值条件。通过2种方法的比较，验证解析方法的正确性。

表1 内倾船主尺度

当波浪船长比/L=1.5，航向角χ=0°时，船舶发生骑浪运动的螺旋桨临界转速与波幅之间的关系如图9所示。由图可以看出，随着波幅值增加，螺旋桨临界转速减低。

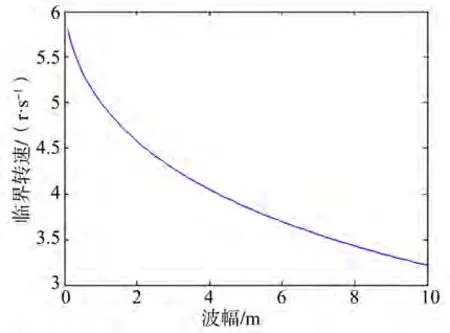
图9 螺旋桨临界转速随波幅变化曲线图

船舶临界船速随波幅的变化如图10所示。

图10 船舶临界船速随波幅变化曲线图

当波幅值增加时，船舶临界航速减低。波幅较大时，临界航速较小，船舶更容易发生骑浪现象。

当波长船长比λ/L=1.5，航向角=0°时，取1/10，基于解析方法和数值方法分析规则波中的船舶纵荡运动。由解析方法得到的螺旋桨临界转速为3.38 r/s，对应临界航速为10.38 m/s。由数值方法得到的螺旋桨临界转速为3.5 r/s，对应的临界船速为10.69 m/s。2种方法得出的结果相差很小，误差在5%左右，从而验证了2种方法的正确性。

当螺旋桨转速为3.4 r/s时，船舶相对于波浪的相对速度和位移分别如图11和图12所示。由图中可以看出，船舶与波浪的相对速度是周期变化的，相对位移随时间增大，即船舶尚未被波浪所捕获，未发生骑浪现象。

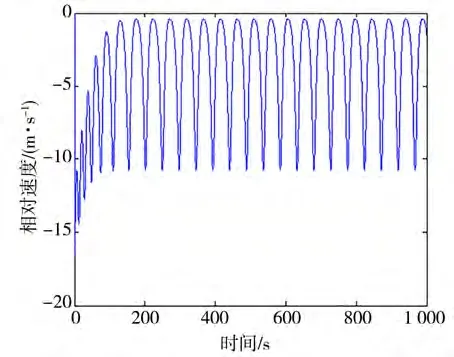
图11 转速3.4 r/s时相对速度时间历程曲线

图12 转速3.4 r/s时相对位移时间历程曲线

当螺旋桨转速增加到3.5 r/s时，船与波的相对速度和相对位移分别如图13和图14所示。由图中可以看出，约200 s后，船舶与波浪之间的相对速度为0，船舶与波浪之间的相对位移也保持为一个常数。表明船舶在运动一段时间后会被波浪捕获，以波浪速度前进。此时，螺舵系统失去对船舶的控制，发生了船舶骑浪运动现象。

图13 转速3.5 r/s时相对速度时间历程曲线

图14 转速3.5 r/s时相对位移时间历程曲线

为了更加准确地判断船舶骑浪运动的发生，以cos(2π·ξ″/)为相图横坐标，船的绝对速度为相图纵坐标，分别给出螺旋桨转速为3.4 r/s和3.5 r/s时船舶运动的相图。由下页图15和图16可以看出：当螺旋桨转速为3.4 r/s时，船舶纵荡运动系统的相图是封闭的，此时船舶运动是稳定的，未发生骑浪现象；当螺旋桨转速为3.5 r/s时，船舶纵荡运动系统的相图不是封闭的，此时船舶运动丧失稳定性，发生了船舶骑浪现象。

图15 3.4 r/s船舶运动相图（未骑浪）

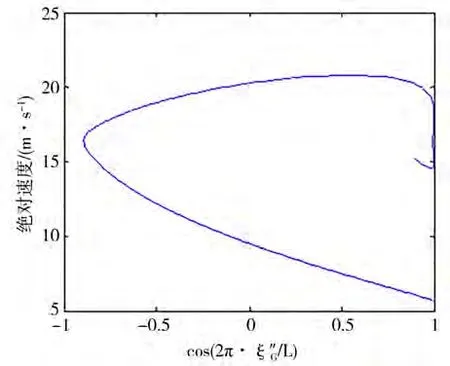
图16 3.5 r/s船舶运动相图（骑浪发生）

取波长船长比/L=1.5，航向角=0°，/= 1/10。针对不同的螺旋桨转速，数值求解船舶纵荡运动，得到运动时历曲线。以螺旋桨转速为横坐标，船舶在波浪中的相对速度运动的稳定响应幅值为纵坐标，给出船舶相对速度随螺旋桨转速变化的分岔图，如图17所示。由图可见：当螺旋桨转速低于3.4 r/s时，船舶纵荡运动是稳定的周期运动，在分岔图的表现上表示为一个点；当螺旋桨转速为3.5 r/s时，分岔图上不能画出点，此处用蓝色的圆点示意非稳定区域，此时船舶纵荡运动开始发散，即船舶发生骑浪失稳运动。

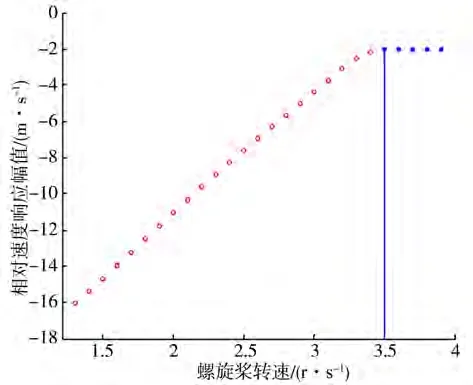
图17 船舶相对速度随螺旋桨转速变化分岔图

2.2 非规则波中骑浪概率研究

建立船舶纵荡运动微分方程，采用随机Melnikov非线性动力学方法，求解船舶在随机波浪中发生骑浪的概率。

通过线性叠加求解随机波浪力：

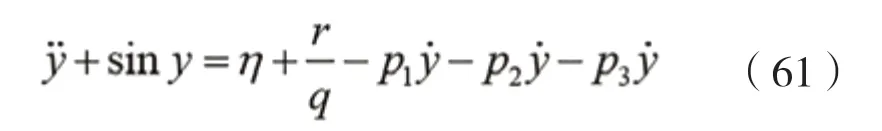
是一个随机过程，其谱密度函数为S。假定不规则波浪力为在规则波的基础上叠加一随机的波浪力，规则波周期和波高为对应波浪谱的谱峰周期和有义波高。基于以上假设，可以表示为如下 形式：

式中：ω为波浪谱的谱峰频率，rad/s；()为随机相位角，rad。

采用Melnikov函数来表征稳定流形与不稳定流形之间的距离，如下表示：

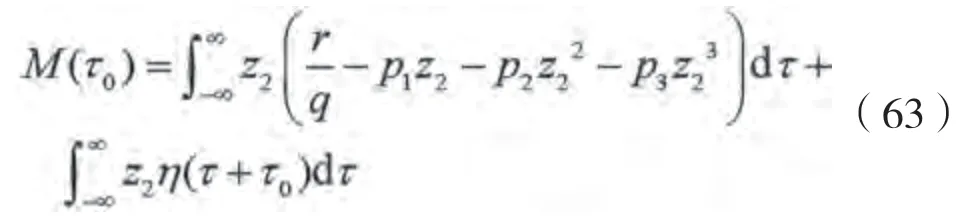
船舶在随机波浪中发生骑浪的必要条件为()<0。随机波浪产生的激励可近似为高斯随机过程，因此通过线性变化得到的Melnikov过程()也是高斯过程，均值μ和方差σ的表达式为：

式中：()为频率响应函数：

正态分布的概率密度函数为：

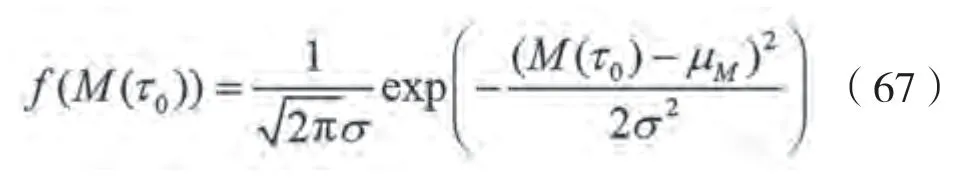
通过积分可得到该正态分布的概率分布函数：

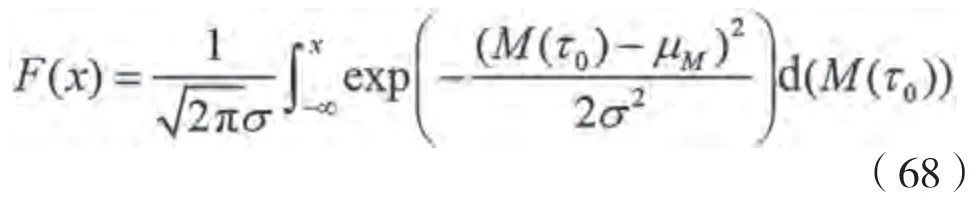
根据上述概率分布函数，随机波中骑浪发生的概率为：

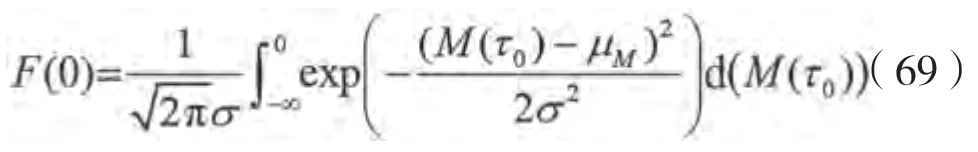
分别研究波高和转速对船舶骑浪发生概率的影响，计算结果如图18和图19所示。随着有义波高的增加，船舶所受到的波浪载荷增加，骑浪概率也随之增加。随着螺旋桨转速的增加，船舶的航行速度增加，当航速越接近波速时，骑浪发生概率 变大。

图18 不同波高下的骑浪概率

图19 不同转速下的骑浪概率

3 船舶横甩非线性分析方法

基于累积艏摇运动原理，建立船舶艏摇运动方程如下：

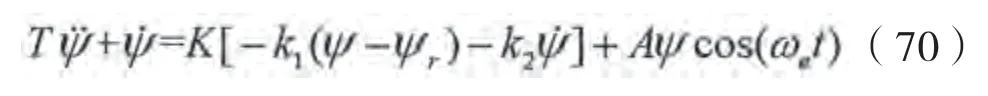
将船舶的艏向角以艏摇偏差角和目标艏向角的方式来表示，引入艏摇偏差角，=-Ψ，将其代入公式（70）可得：

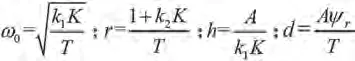
引入时间尺度=，将其代入式（71）得到如下表达式：

引入小参数，并在计算完成后令小参数=1，式（72）变换为：

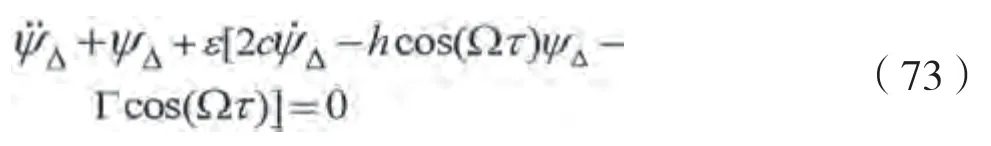
为研究艏摇运动的亚谐共振，令船舶遭遇频率与固有频率的比值满足Ω≈2，并引入频率比调谐因子来描述频率比与2之间的差异，令：

将式（74）代入式（73），整理可得：

假设方程（75）的解为：

根据多尺度法，可得到方程的一阶近似解为：

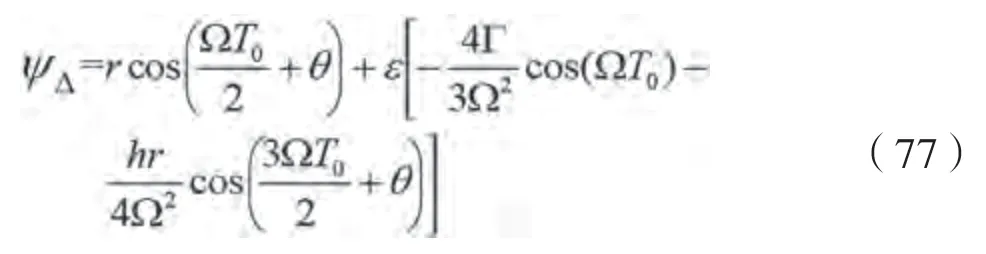
式中：变量和变量由如下两式确定：

根据消除永年项条件，可得：

将公式（80）的近似解表达为：

式中：B、B都表示为实数，将表达式（81）代入到表达式（80）中，将方程的实部和虚部分离开，可得：

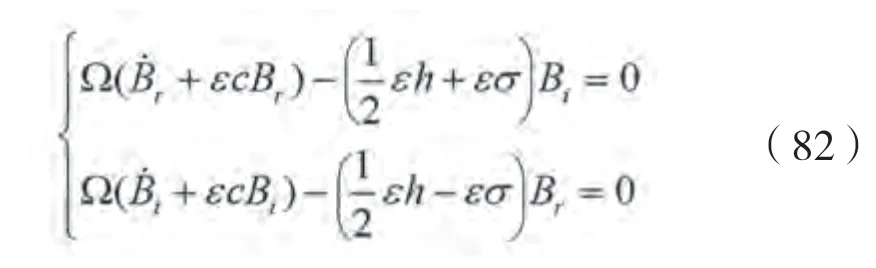
设方程（82）的解分别为：

式中：b和b都为常数，将公式（83）代入到公式（82）中可得到：

由此得到艏摇运动的稳定域和不稳定域如图20所示，在频率比为2时，船舶艏摇运动方程中的参数激励项在达到0.62左右时就会发生失稳。

图20 解的稳定性区域图

以波高为分岔参数，得到船舶艏摇运动响应幅值随波高变化的分岔图，见下页图21。在 2倍频波浪条件下，当波高<0.7 m时，系统为稳定的周期运动，在分岔图的表现上表示为1个红点。当波高＞0.7 m时，发生船舶发生艏摇失稳运动。

图21 2倍频下船舶艏摇角随波高变化分岔图

由下页图23和图24可见，当波高取为1 m时，船舶在经过几个周期后，艏摇运动幅值越来越大。此时参数激励的作用明显增加，引起艏摇运动发生亚谐共振，此时相图不再是1个闭合的圆圈，而是螺旋线，即船舶艏摇运动不断增大导致丧失稳定性，发生船舶横甩现象。

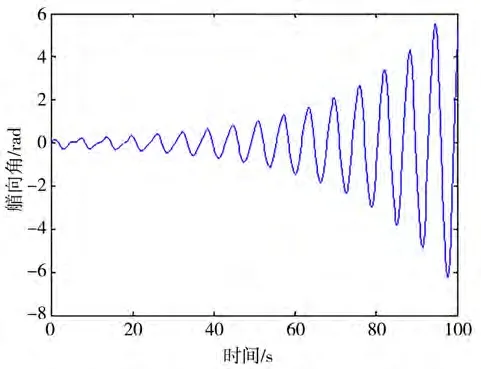
图24 波高1.0 m艏摇角时间历程曲线图

由图22和图23可见，当波高为0.5 m时，参数激励较小，不能激起系统的亚谐共振，船舶艏摇运动的相图构成1个闭合的圆圈，船舶艏摇运动是稳定的，不会发生艏摇失稳现象。

图22 波高0.5 m艏摇角时间历程曲线图

图23 波高0.5 m船舶艏摇运动相图

图25 波高1.0 m船舶艏摇运动相图

4 结 论

本文回顾总结了基于非线性动力学理论和方法开展船舶在波浪中的运动、倾覆过程和运动失稳机理研究的主要进展。主要结论如下：

（1）船舶运动（尤其大幅运动）是非线性动力系统、非线性动力学方法与耐波性理论的结合，是船舶稳性研究的重要发展方向；

（2）非线性动力学方法可以更为精准和方便地描述船舶的瞬时运动状态，比如采用相图可以给出船舶瞬时的运动速度、幅值和趋势等；

（3）采用哈尔米顿系统分析轨道的同宿与异宿，可以确定船舶不同运动形式（例如骑浪、横甩）的稳定与失稳域的范围；

（4）船舶失稳导致运动过程出现不同状态，采用分叉方法研究船舶运动失稳的不同状态（包括倾覆）是可行的方法；

（5）今后研究的方向是将耐波性理论、波浪理论及非线性动力学理论相结合，探索船舶运动和稳性研究的新概念和新方法，开辟船舶运动和稳性研究的新途径和技术手段，使船舶运动安全的研究和表达更为精准。