考虑最优会面位置的多车型拼车优化调度模型
2022-08-18胡忠恺袁鹏程高洪振
胡忠恺,袁鹏程,2,高洪振
(1.上海理工大学 管理学院,上海200093;2.上海理工大学超网络研究中心,上海200093;3.青岛市城市规划设计研究院,山东青岛266000)
0 引言
近年来,Uber、Aribnb等一系列共享平台逐渐出现在人们的视野中,“共享经济”热潮不断袭来。而在此背景下网约车合乘已成为共享经济发展中一种主流的交通出行方式,虽然一般情况下合乘可以满足客户门到门的出行需求,但客户因司机未在其期望的会面位置进行接送而造成满意度大打折扣的情况时有发生。因为道路交通安全法对于车辆临时停车有一定的规定,司机极有可能因为违停面临交通处罚从而增加不必要的支出。而新冠疫情的爆发加剧了此类现象的发生,疫情期间各地社区纷纷采取科学合理的防控措施,部分社区合并成一个大的社区实施封闭式管理,原则上只保留几个进出通道。由于司机属于社区外人员不能直接进入社区接送客户,所以只能在社区外选择某一位置与客户会面,客户和司机需要在进出口附近寻求一个最佳的地点作为实际的会面点,从而不仅能保证客户对会面位置的要求也能避免会面位置的不佳选择导致的司机过多绕路、客户等待时间过长等问题。
而随着网约车平台的不断发展与完善,越来越多的车型加入到网约车的队伍中,常见的网约车类型有:紧凑车、中级车、豪华车、SUV等,一般是5~7座的小型载客车辆,而不同类型的车辆所对应的车辆燃油费等都各不相同。因此网约车平台在派出车辆为客户提供服务前通常会考虑车辆类型对成本所造成的影响,并在满足客户要求的前提下尽量降低成本以达到利益最大化。综上所述,将最优会面位置和多车型因素结合起来考虑对网约车合乘来说是至关重要的。
1 相关研究
目前,国内外在网约车合乘模型构建方面,众多研究主要考虑目标函数和约束条件对模型的影响且已经有了一定的成果。而就优化目标而言主要集中于优化运营成本目标和服务质量目标,许多关于合乘模型的目标函数都是优化单个运营成本,也有部分文献考虑了运营成本和服务质量相结合的多目标系统。在单目标优化模型中,为了确保能满足客户所需的最低服务水平服务质量因素通常以约束条件出现。例如在Wolfler Calvo的文章中,以合乘的总出行时间最短建立目标函数,但对未提供服务的请求设置了惩罚函数,在这种情况下,需要较大幅度地扩展合乘的服务范围以满足客户需求。一些研究考虑了以最大化合乘总利润或者最小化DARP运营总成本为目标建立模型。除此之外,还有不少文献考虑了一些更具体的问题作为目标,Guerriero等人以所需车辆最少为目标,Atahran等人以车辆排放量最小为目标,Garaix等人以最大化客户乘坐率为目标构建模型。
综合以上分析,目前国内外对网约车合乘模型的研究大多数是考虑单一车型下司机和客户会面位置确定的合乘模式,并在此基础上考虑时间窗等约束,而在模型研究中还没有相关文献将车辆类型和最优会面位置作为约束条件进行综合考虑。一方面,以往研究中没有加入对不确定性会面地点因素的考虑;另一方面,单一车型的合乘不能满足网约车平台规模的发展需要以及客户的多元化需求,现实中用于合乘的网约车车辆类型也趋于多样化,而且不同车型的车辆各特征都不相同,对合乘过程也造成了不容忽视的影响,因此需要构建新的模型。本文以后疫情时代为背景,以DARP模型作为基本模型,以运输总成本为目标建立基于车型类别考虑最优会面位置的网约车合乘优化模型。
2 问题描述
基于车辆类型考虑最优会面位置的网约车合乘优化问题可描述为:现有网约车平台派出一定数量不同车型的车辆提供合乘服务,已知有一定数量的客户发出合乘请求以及每个客户的需求量和其所能接受的合乘最大车型,各客户向平台提供能接受的多个会面位置供司机选择其中一个地点作为真实会面点。因此每个客户各自相对应的多个可能的接送位置中只能有一个接送位置被且只被访问一次,即每一个客户应由同一辆车为其完成合乘服务。每辆车所访问的客户需求总和不能超出车辆的最大负载能力,并要求车辆对每个客户的服务时间必须在其要求的时间范围内开始。目标是在所有的约束条件被满足的情况下,尽可能找到最科学合理的车辆使用方案、车辆行驶路径以及车辆访问客户的先后顺序,保证车辆以最小的运输总成本完成合乘任务。
如MVDARP-M场景图(见图1)所示,网约车平台存在多种类型的车辆提供合乘服务,均从车辆的出发节点驶出,然后为客户1、2和3提供服务,而客户1、2和3均存在三个不同的出发节点和目的地节点,图1中网约车平台提供了两种类型的车辆。车型1车辆从起始节点出发为客户1和2提供服务,并分别在客户1和客户2的所有出发节点中选择其中一个作为客户实际的上车位置,再将所有客户送往各自相对应的目的地之后车辆驶入目的地节点;车型2车辆从起始节点出发为客户3提供接送服务。
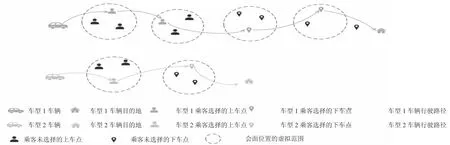
图1 MVDARP-M场景图
3 模型建立
3.1 模型的假设
通过对本文所研究问题的描述,为建立模型需要作出以下假设:任意两节点之间的距离为点到点之间的最短运输距离,所有类型车辆在运输过程中均匀速行驶,不考虑交通堵塞、交叉口红绿灯、车辆损坏以及其他特殊情况的影响;所有车型的属性都是已知的,包括车辆载重量、运输成本、使用成本等;所有客户的需求量以及客户所能接受的最大车型已知;各客户的所有节点位置以及服务时间要求已知;每辆车可以为多名客户提供服务,但每名乘客只能由一辆车完成服务,且服务期间不允许出现换乘的情况。
3.2 模型符号说明
(1)集 合
N=S∪D∪{0,2n+1}为节点集合,其中0表示车辆的起始节点,2n+1表示车辆的目的节点;
S={1,… ,n}为客户的上车节点集合;
D={n+1,…,2n}为客户的下车节点集合;
Z={1,… ,m}为集合N中各节点所对应的可选择的节点集合;
K={1,… ,k}为车辆类型集合;
G={1,… ,g}为k类型车辆的集合。
(2)参 数
L为客户的最大乘车时间;
M为k类型车辆产生的单位固定成本;
C为k类型车辆的单位运输成本;
Q为k类型车辆车型系数,车型越大,车型系数越大;
o节点p的第i个节点的客户能接受的最大车型系数;
f为车辆提前到达客户点时产生的单位时间惩罚成本;
f为车辆延迟到达客户点时产生的单位时间惩罚成本;
Q为k类型车辆的最大载重量;
T为k类型车辆行驶路线的最大总时长;
d为车辆在节点p的第i个节点的服务持续时间,p∈N,i∈Z;
W为车辆在节点p的第i个节点的载重量;
e为节点p所对应的第i个节点的客户期望最早服务时间;
l为节点p所对应的第i个节点的客户期望最晚服务时间;
ee为节点p所对应的第i个节点的客户可接受的最早服务时间;
ll为节点p所对应的第i个节点的客户可接受的最晚服务时间;
t为节点p的第i个节点到节点q的第j个节点的行驶时间;
D为节点p的第i个节点到节点q的第j个节点的距离。
(3)变 量
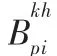
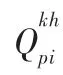
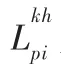

3.3 目标函数说明
本文所构建模型的目标函数是在疫情背景下实现网约车合乘的运输总成本最小,由于本文考虑的问题是多车型合乘研究,因此不同车型车辆都有各自不同的固定使用成本和单位距离运输成本。而运输成本包括三部分:第一部分是车辆的固定使用成本,由公式(1)表示;第二部分是车辆的运输成本,由公式(2)表示;第三部分是车辆的时间惩罚成本,由公式(3)表示。
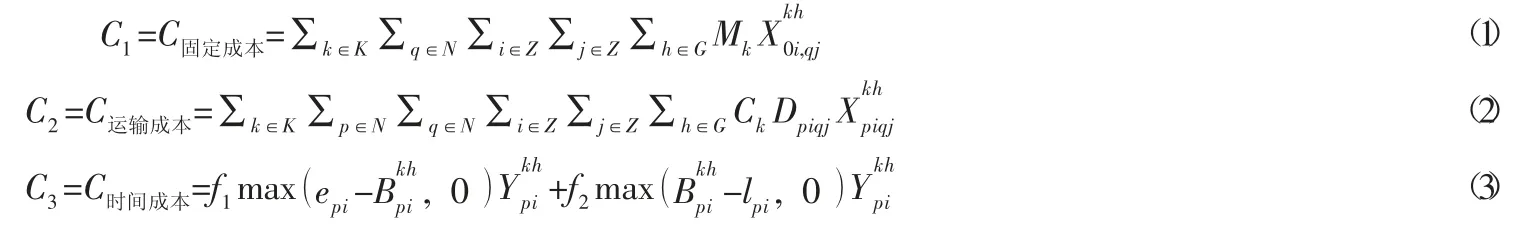
3.4 模型建立
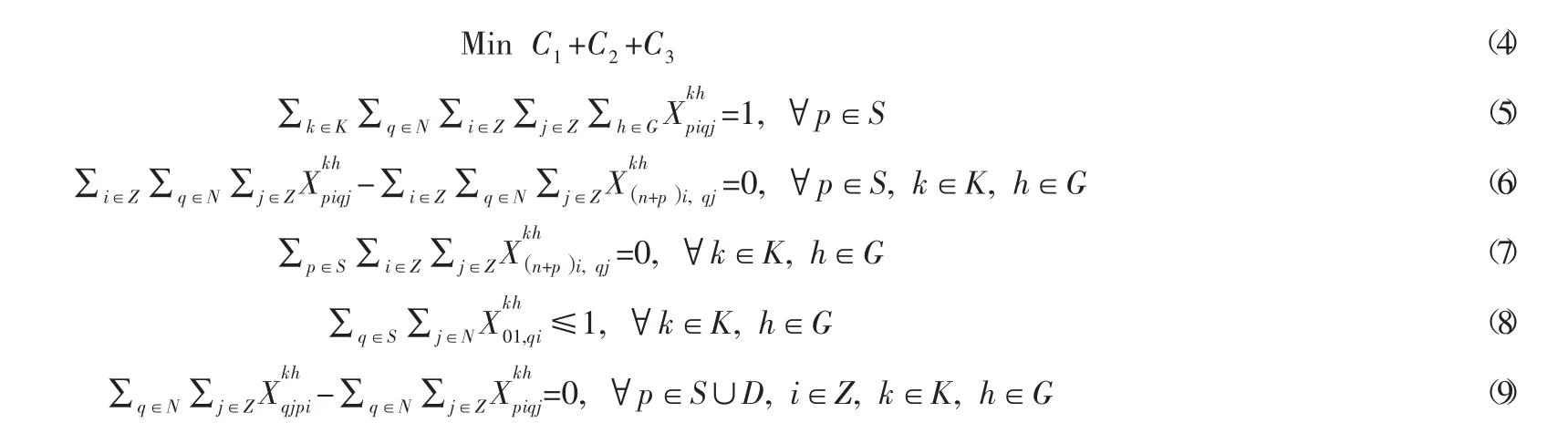
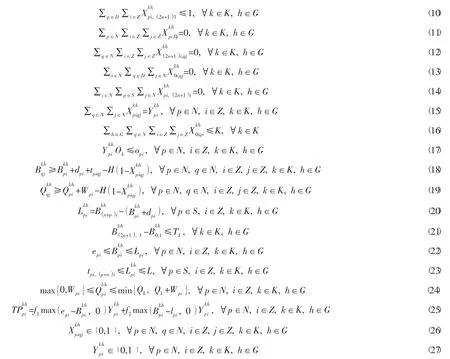
其中:式(4)为目标函数即总成本最小化。式(5)至式(27)为约束条件。其中式(5)表示每个发出合乘请求的用户恰好被服务一次;式(6)表示同一辆车访问客户的出发节点和其对应的目的节点;式(7)表示不允许车辆先访问客户的目的节点,再访问客户的出发节点;式(8)至式(10)表示提供合乘服务的车辆从车辆的出发节点开始,到车辆的目的地节点结束;式(11)表示车辆在服务过程中不允许访问车辆的出发节点;式(12)表示车辆到达车辆的目的地节点后不会再驶出提供服务,即服务车辆最终都会停在车辆的目的地节点;式(13)表示车辆从车辆的出发节点后必须先访问某客户的出发节点再访问该客户的目的地节点;式(14)表示车辆不允许从客户的出发节点直接访问车辆的目的地节点;式(15)表示车辆是否访问某个节点;式(16)表示任意车型的服务车辆使用数不超过该车型总的车辆数;式(17)表示服务车辆的车型系数要小于或等于所服务客户点的最大车型系数;式(18)和式(19)分别表示时间的一致性和负载变量的一致性,其中H是一个非常大的常数;式(20)为每个客户在车辆k上的乘车时间,并且该时间会受到式(23)的约束,而式(23)也被用作优先约束,式(21)限制了每辆车行驶路径的总时长;式(22)表示车辆需在客户要求时间窗内提供服务;式(24)为各类型车辆的容量约束;式(25)为惩罚函数的表达式;式(26)和式(27)表示决策变量为0~1变量。
4 算例分析
4.1 算例描述
假设在上海市某一路网中已知存在86个节点位置。其中有两个节点分别作为所有服务车辆的出发节点和目的地节点,客户的所有节点共有84个。平台提供三种类型的车辆供客户选择,且每种车型有2辆车可提供服务。在该路网中共有14个客户发出请求,且每个客户各自都对应三个不同的节点供选择。本文用[0,40]×[0,4 0]的矩形区域来表示该路网范围,车辆和客户的所有节点位置都随机且独立的均匀分布在该区域内。各种车型的单位运输成本、固定使用成本、车型系数、车辆数以及最大载重量如表1所示,各节点位置坐标以及时间窗要求、车型系数要求、需求量要求等如表2和表3所示。

表1 各车型的车辆参数
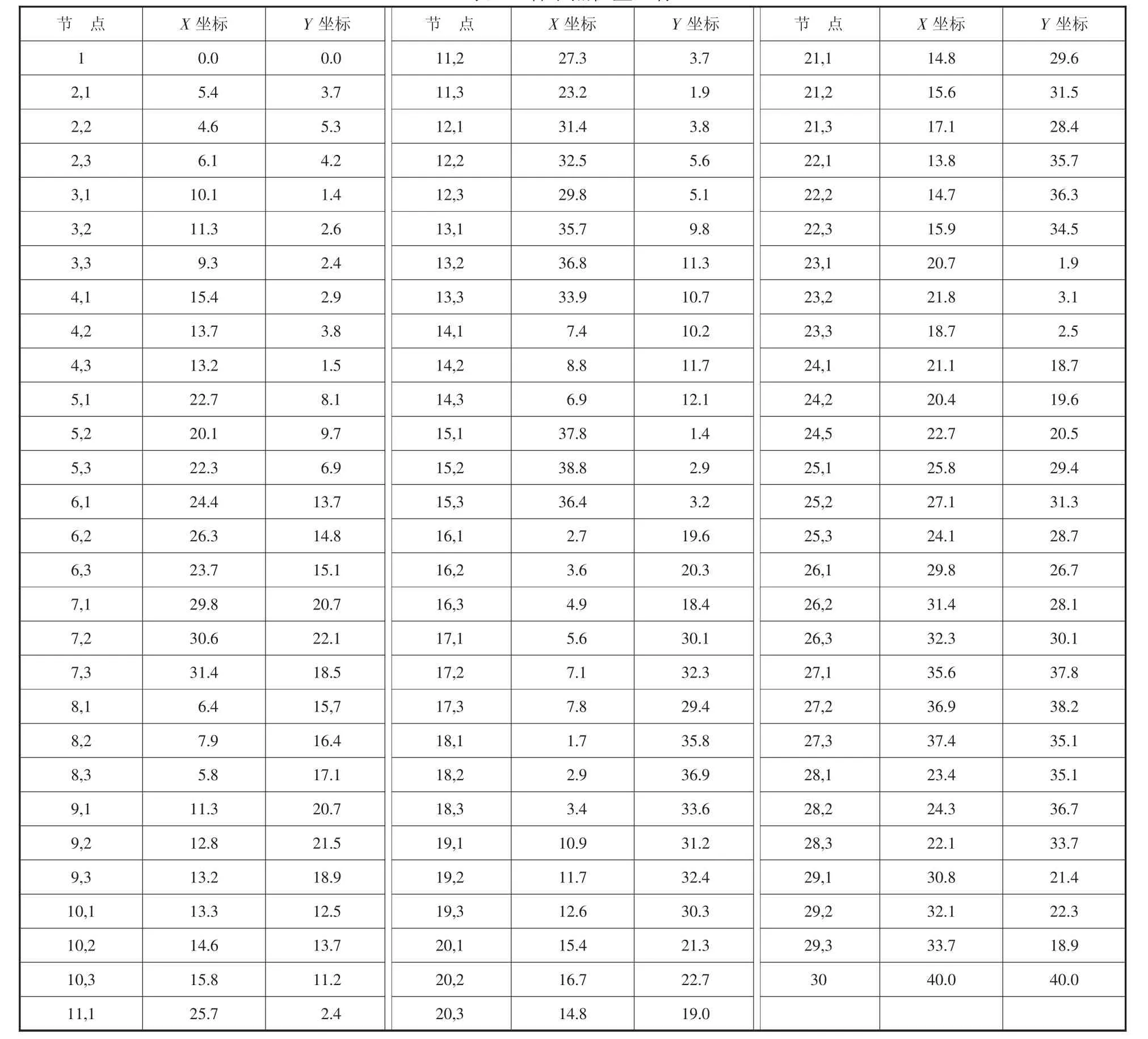
表2 各节点位置坐标
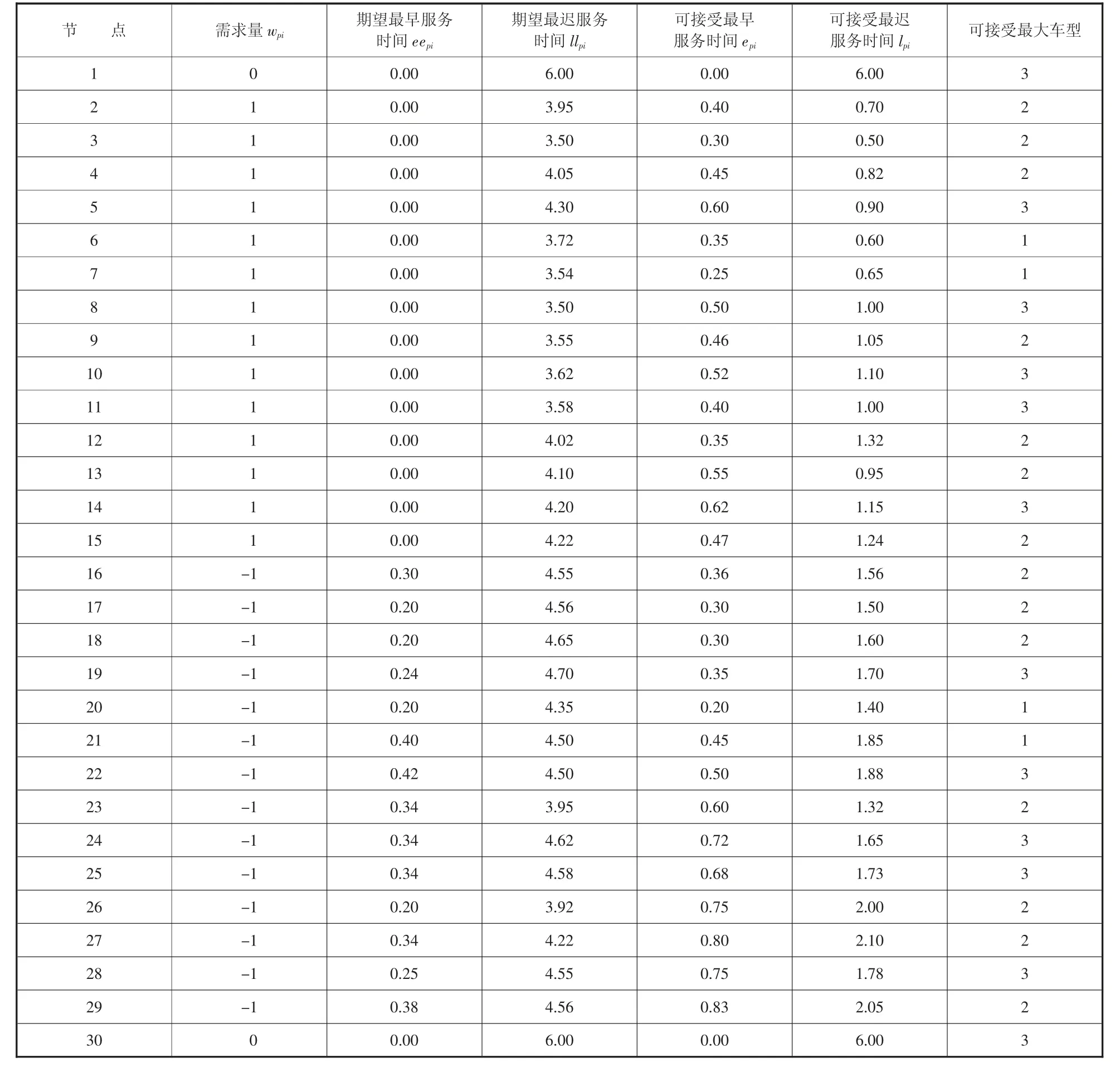
表3 各节点特征数据
4.2 算例结果
基于上文表中给出的节点和各车型数据利用Lingo18.0软件求解本文构建的MVDARP-M模型,将计算结果进行整理得到的最优接送方案和合乘路径如表4所示。由表4可知,共需六辆车完成合乘服务,即派出三种不同车型的车辆各两辆,总行驶距离为537.75公里,总运输费用为875.90元,并形成六条合乘路径。
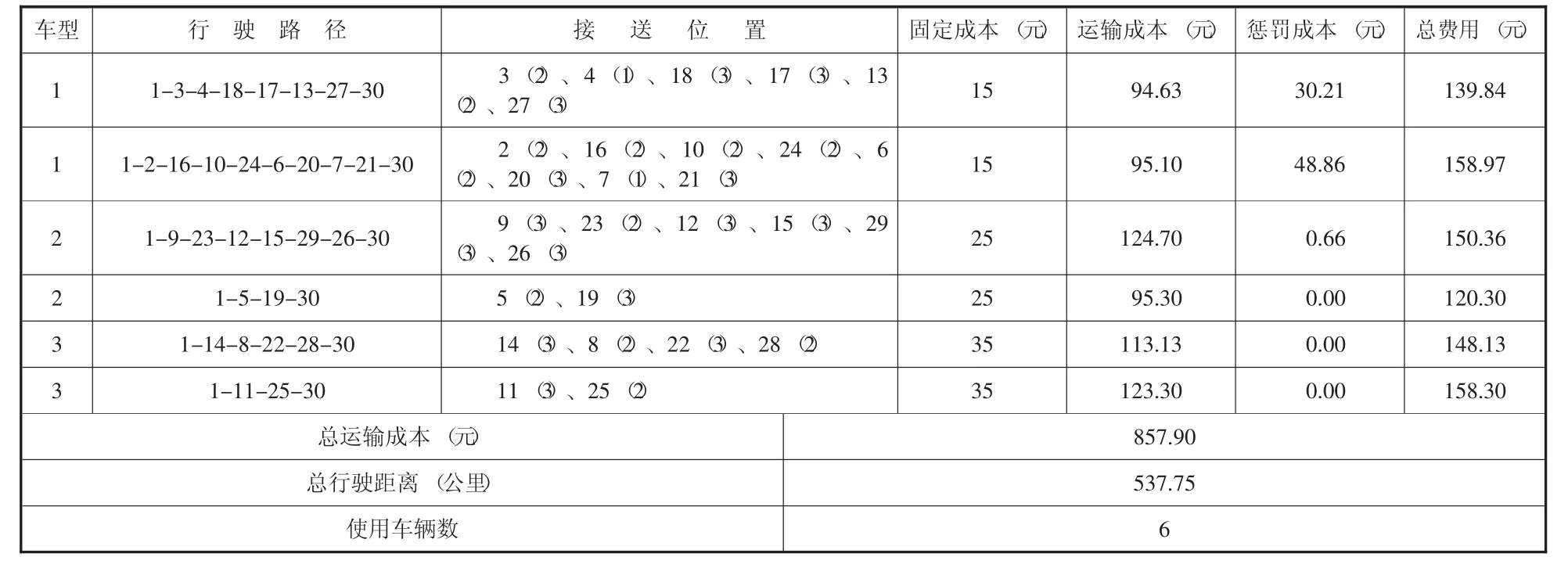
表4 最优合乘方案
4.3 方案对比分析
上述算例是在车型不同且车辆数有限的情况下得到的最优合乘方案,并且选择最优的会面位置提供合乘服务。为了验证该方案的优化效果,将该优化方案与未考虑最优会面位置的合乘情况进行对比分析,给出未考虑最优会面位置的合乘方案如表5、表6所示。未优化方案是在所有基本数据保持不变的情况下满足各约束条件,并在每个客户所有可能的接送位置中分别随机选择会面地点而得到的合乘路径。从表5、表6可以看出未优化方案仍是提供三种车型的情形下得到的合乘方案,且未对会面位置进行最优的选择。未优化合乘方案1中,平台派出六辆车提供服务并形成六条路径。未优化方案1中车辆总运输成本为1 053.70元,总行驶距离为635.45公里,未优化方案2中车辆总运输成本为1 247.76元,总行驶距离为711.99公里。具体的合乘路径以及各类成本等数据如表5、表6所示。
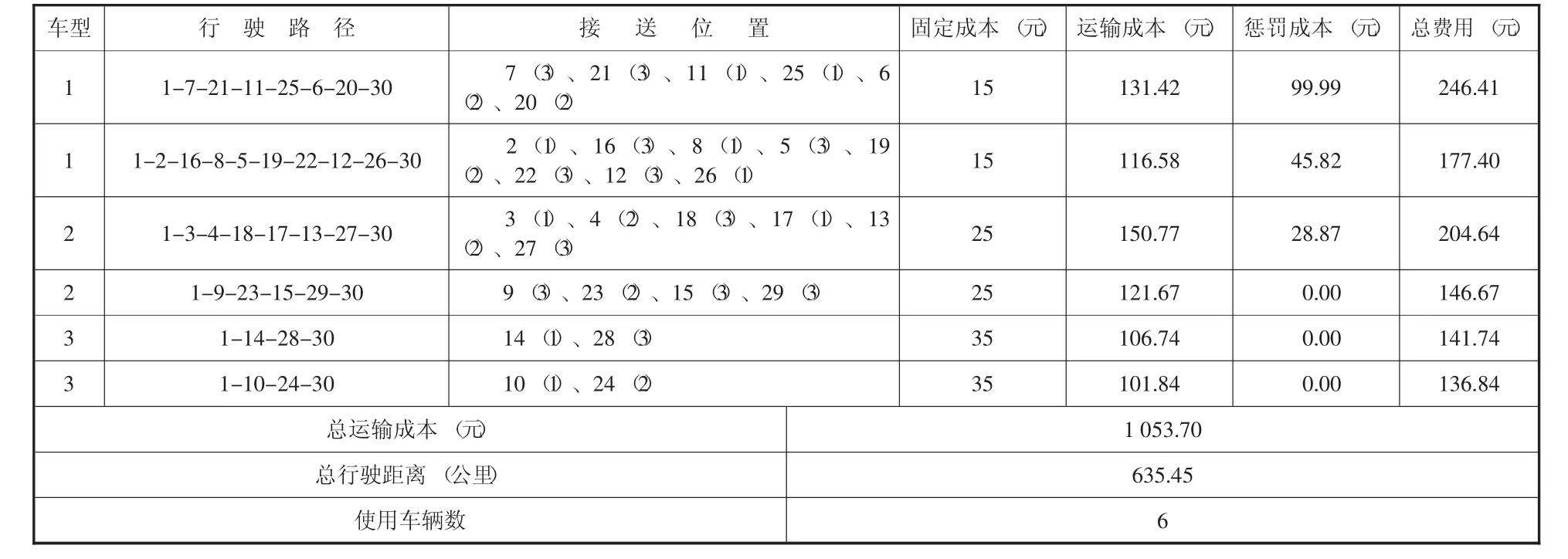
表5 未优化合乘方案1
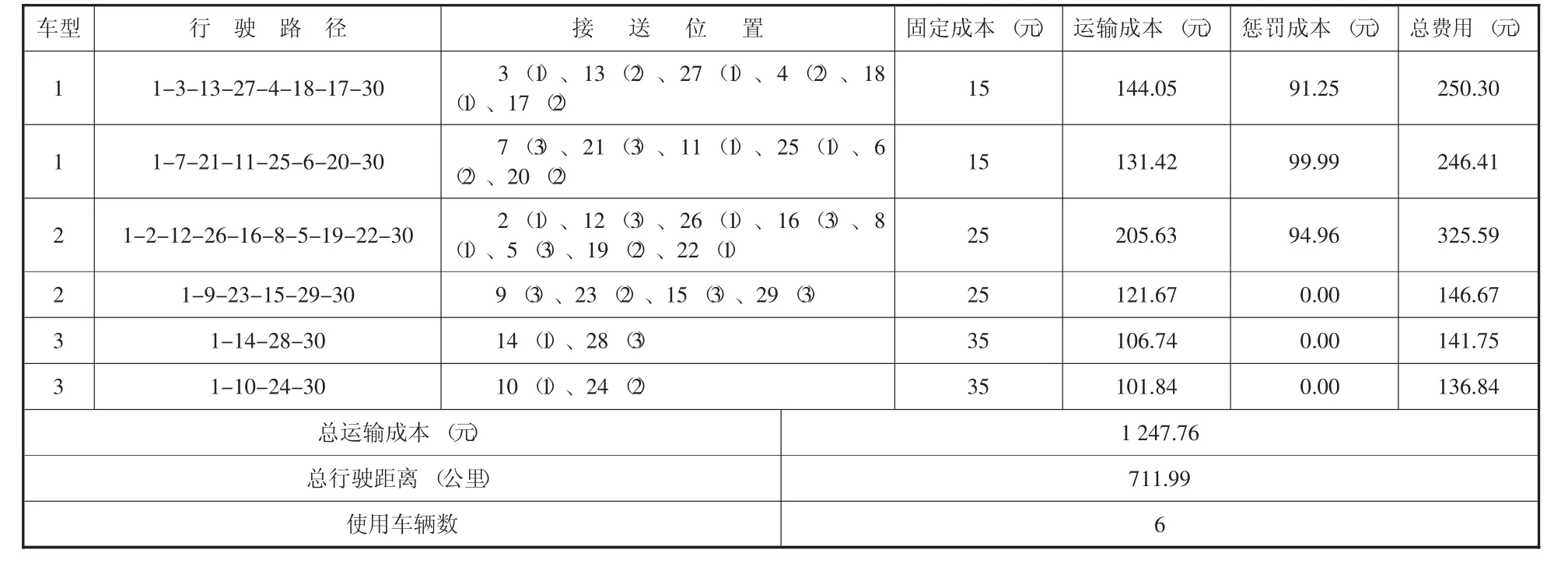
表6 未优化合乘方案2
相较于未优化的合乘方案,考虑最优会面位置的多车型网约车合乘最优方案的总运输成本分别节省了177.8元、371.86元,总行驶距离分别减少97.70公里、174.24公里,即成本费用率分别降低20.30%、42.45%,行驶距离分别降低18.17%、32.40%。而且在网约车实际的合乘方案中,因为客户地点的不确定性容易产生客户找不到司机或者司机找不到客户的情况,从而可能造成实际成本和行驶距离的进一步增加。所以优化方案极大可能比现实的合乘方案更有优势,不仅能在一定程度上减少车辆行驶距离,而且较大幅度地减少了总运输成本。通过对比分析表明,本文得到的优化方案能够为平台产生一定的经济效益且是合理有效的,进一步说明本文所构建的基于车型类别考虑最优会面位置的网约车合乘优化模型的有效性,能够为实际的网约车合乘问题提供参考价值。
5 结论
在后疫情时代的大背景下,本文基于DARP问题,提出了所要研究的网约车合乘问题MVDARP-M,并综合考虑了网约车车辆的运输成本、固定成本以及时间惩罚成本建立了基于车型类别考虑最优会面位置的网约车合乘优化模型。将多车型的网约车合乘优化方案分别与单一车型且未选择客户最优接送位置的三个方案的运输总成本及运输总距离进行对比,验证了模型的适用性和有效性,可为疫情下的合乘车辆路径优化和网约车平台调配车辆提供理论依据。基于本文所研究的是多车型的合乘优化且仅考虑燃油车,而新能源汽车的崛起越来越受到人们的关注,而在实际情况中,电动汽车正不断加入到网约车的队伍中。因此在车型中加入新能源汽车对合乘的影响可考虑作为下一步的研究方向。
