车辆合乘问题的分布式复合变邻域搜索算法*
2019-02-13郭羽含
郭羽含,伊 鹏
辽宁工程技术大学 软件学院,辽宁 葫芦岛 125100
1 引言
近年来,随着国民收入和购买力的增长,驾驶私家车已成为人们的主要出行方式。截至2016年末,我国私人汽车保有量已达16 559万辆[1],私人汽车保有量增长的同时也带来了交通拥堵、环境污染等负面问题。随着互联网与共享经济的发展,车辆合乘的出行方式逐渐在大中型城市涌现,车辆合乘问题也引起了学术界的关注[2-4]。早期的车辆合乘模式以出租车搭载多名路途相近乘客的形式出现。这种模式虽然满足了更多乘客的出行需求并在一定程度上降低了其出行成本,但仅依靠这种合乘模式并不能从根本上减少私人汽车的出行数量以缓解其引起的社会问题。针对大中型城市人口工作地点集中但居住分散的特点,本文提出一种合乘关系较为固定且长期保持的车辆合乘模式,该出行模式不但可以减少私家车的出行率,减缓交通压力和环境污染,还可在较大程度上降低人们的出行花费。
目前国内外关于车辆合乘问题的研究有:邵增珍等人利用匹配度聚类算法求解单一车辆的合乘问题,但未涉及多车辆合乘[5-6];周和平等人对合乘者的费用分担与路径选择同时进行优化,综合考虑驾驶员与出行者利益,以出行者时间费用成本最小为目标函数,设计相应的遗传算法对其进行求解[7];Li等人将车辆合乘优化问题转化为基于图的模型问题,利用贪婪集合覆盖算法来解决合乘问题[8];Armant等人对于车辆合乘问题提出三种混合整数规划模型[9];Kleiner等人通过引入个人偏好与价格竞争机制来促使人们进行车辆合乘,但由于其系统限制,一位司机只能与一位乘客合乘,且缺乏大规模的实验论证其性能[10];Simonin等人通过建立一个互联网系统来解决人们动态合乘的需求[11];Rahimi-Vahed等人提出的路径重新链接算法用以解决合乘问题,但对于规模较大的合乘问题求解效率不高[12]。综合来看,现有研究的模型和算法[13-14]在高效求解大规模多车辆合乘问题上存在局限性。
对于合乘关系长期保持的长期车辆合乘问题(long-term carpooling problem,LTCPP),本文提出了涵盖车容量和时间窗约束的全面数学模型[15-16],并在变邻域搜索的基础上提出了一种基于分布式的复合变邻域算法。本文将变邻域算法与分布式计算相结合,可以高效求解大规模车辆合乘问题,并有效避免了由于变邻域算法随机性而产生质量较差优化结果的问题。实验结果表明该算法求解质量高且求解速度快,对于大规模的算例具有较好的实用性。
2 车辆合乘问题数学模型
2.1 问题定义
长期车辆合乘问题中每位合乘参与者都拥有车辆,且具有相近的目的地。每位合乘参与者与其他合乘参与者互相组成合乘小组,组内用户每天轮流接送组内其他用户抵达目的地。问题的目标是在满足合乘参与者约束的条件下将其分配到若干个合乘小组中,最终得到总出行成本最低的合乘方案[17]。合乘小组中司机接送组内其他用户的路径概况如图1所示。

Fig.1 Overview diagram of carpooling group route图1 合乘小组路径概况图
2.2 合乘模型符号定义
2.2.1 常量定义
数学模型中常量如表1所示。

Table 1 Constants used by model表1 模型使用的常量
2.2.2 变量定义
数学模型中变量如表2所示。
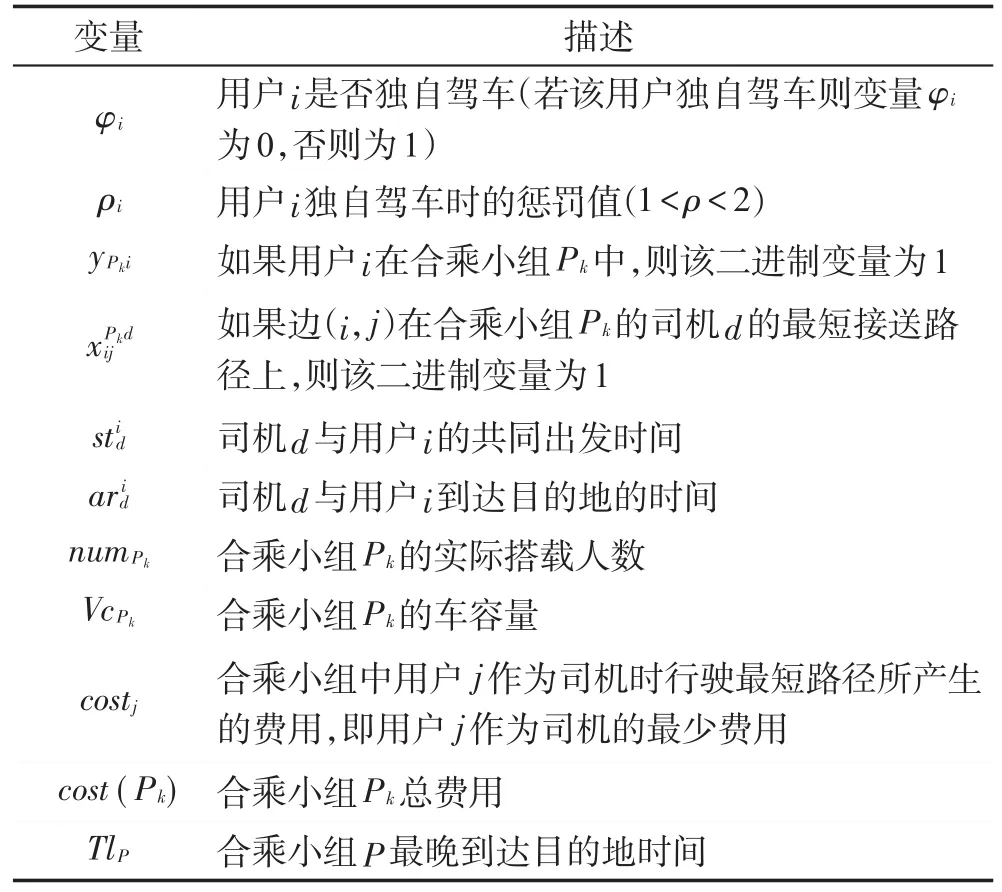
Table 2 Variables used by model表2 模型使用的变量
2.3 目标函数
LTCPP以用户总出行成本作为优化目标,合乘小组中每位用户作为司机时,该用户可以有多种接送顺序接送组内其他用户,因此对应着有多条行车路径,本文通过路径规划算法对合乘小组中每位作为司机的用户规划出一条最短的接送路径及相应的接送顺序,为了鼓励用户与其他用户合乘并减少用户单独驾车的可能性,在此引入了惩罚因子ρ(1<ρ<2),未与其他用户合乘的用户将会受到惩罚付出更多的费用。合乘小组Pk总费用cost(Pk)定义如下:
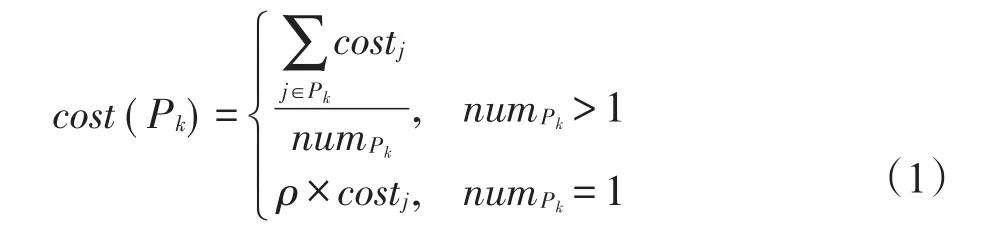
则有目标函数:

其中,fLTC为所有合乘小组的出行成本之和。
2.4 数学模型
长期车辆合乘问题的数学模型表示如下:

式(3)和式(4)表示司机d将用户i和用户j加入到合乘小组P中;式(5)表示连续性约束;式(6)表示单独出行的用户需受到惩罚;式(7)和式(8)表示合乘小组载客量约束;式(9)和式(10)表示合乘小组P最晚到达目的地时间约束;式(11)表示合乘小组中司机d的行驶时间约束;式(12)表示司机接送用户的时间约束;式(13)~(15)为二进制完整约束;式(16)和式(17)为非负约束。
3 LTCPP合乘方案
3.1 合乘方案表述
LTCPP合乘方案表述的目的是在待求解问题和算法生成的解决方案之间建立一个完整的映射。LTCPP的合乘方案包括将用户划分到各个合乘小组,并在组内用户作为司机时描述司机接送组内其他用户的路径。鉴于该问题涉及分组方式和行驶路径,因此合乘方案需要能够表述组内每个用户的路径信息。合乘方案设计为两层。第一层显示各个合乘小组的用户信息,而第二层则记录组内用户作为司机时接送组内其他用户的路径。此外,在第二层中,还显示与组内每个用户相关联的一些其他信息,例如总行驶时间和距离,当该用户作为司机时接送其他用户的时间,以及该用户是否与其他用户合乘。
在第二层表述组内每位用户i作为司机时的相关信息,其中包括用户i的行驶路径Ri、出发时间及到达其他用户所在地点的时间Ti、是否与其他用户合乘φi、行驶路程disi、行驶时间ti及到达目的地时间avti。合乘方案表述示意图如图2所示。
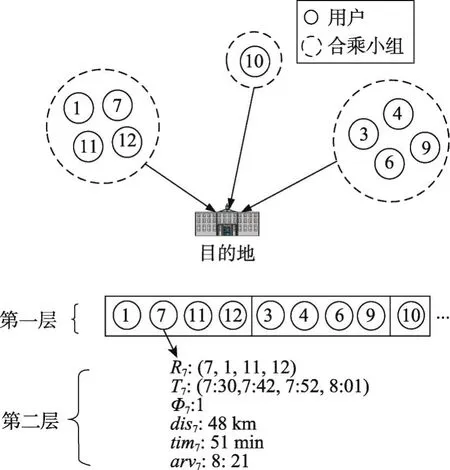
Fig.2 Presentation diagram of carpooling solution图2 合乘方案表述图
3.2 初始合乘方案
为了得到质量较高的初始合乘方案,本文采用了两步法。
第一步选择n个用户来构建n个合乘小组。此n个用户作为每个合乘小组的初始司机,其余未被选择为司机的用户将被分配至以上合乘小组中。具体步骤如下。
所有用户按照随机顺序放入用户集合中。从列表中随机选择用户a来构建合乘小组,然后从用户集合中删除用户a和距离用户a最近的m个用户,其中m为通过对所有用户的搭载人数求平均值而获得的整数,如式(18)所示。

然后,从用户集合的剩余用户中随机选择用户b来构建另一个合乘小组,继而将用户b和用户集合中距离用户b最近的m个用户移除。当所有用户从用户集合中删除时,该过程结束。
这种机制避免了选择两个距离过近的用户构建两个合乘小组,从而保证合乘小组中用户的均匀分布,为下一步算法提供了良好的基础。
在第二步中,本研究设计了一种Regret Insertion算法。该算法针对在第一步中未被选择为司机的所有用户的Regret值进行计算,以便将这些用户分配到各个合乘小组中。
首先,通过式(19)计算每一位在第一步中未被选择为司机的用户i和被选为司机的用户j之间的距离dij。
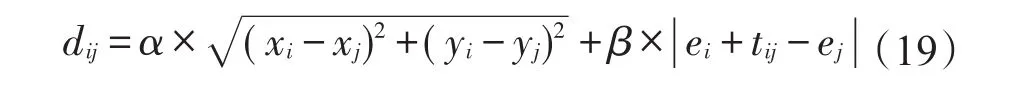
其中,(xi,yi),(xj,yj)分别为用户i和用户j的坐标;ei和ej为用户i和用户j的最早出发时间;tij为用户i到用户j的行驶时间;α和β为调整参数。
然后,计算用户i的Regret值,即上文中计算的第二短距离dij和最短距离dik之差,如等式(20)所示。

该算法在分配用户时优先分配Regret值最大的用户,避免将其分配到第二近的司机所在的合乘小组,使得合乘方案的质量产生较大幅度的降低。该分配过程受合乘小组车容量约束限制,用户不能被分配到超出车容量限制的合乘小组中,如果离用户最近的司机所在的合乘小组人数达到车容量限制,则依次尝试将该用户分配至下一个最近的司机所在的合乘小组。当所有未选择的用户均被分配至合乘小组中或者不可能再将任何未选择用户分配到任何合乘小组时,该过程停止分配,未被分配的用户被视为单独驾驶。
为降低算法的复杂度,在用户分配阶段未检查行驶时间和时间窗约束。因此,需要在分配结束后对各合乘小组进行约束验证及修复以确保初始合乘方案中所有的合乘小组均满足行驶时间和时间窗约束。如果合乘小组违反行驶时间和时间窗约束,将被修复为符合约束且出行成本增长最少的两个或多个合乘小组。修复过程具体如下,其中n的初始值为2。
(1)选出该合乘小组中n个相互距离最远的用户作为新的n个合乘小组的司机。
(2)将其余用户按照Regret Insertion算法分配到新的合乘小组中,并执行步骤(3)操作。
(3)若新的合乘小组满足行驶时间和时间窗约束,修复过程结束。否则对该合乘小组进行重新修复,将n的值加1,并执行步骤(1)操作。
获取初始合乘方案的算法设计如下所示:


4 变邻域搜索
为了使变邻域搜索算法适应本文特定的长期车辆合乘问题,需定义针对本问题的邻域结构,建立适用于合乘方案的搜索过程,并且利用Spark分布式平台将算法部署到多台计算机上进行并行计算。
4.1 邻域设计
根据长期车辆合乘问题的特点,本研究设计了四种不同的邻域搜索Nk(S),四种邻域搜索分别为混合邻域(mixed neighborhood)N1、链式邻域(chain neighborhood)N2、分割邻域(divide neighborhood)N3和合并邻域(merge neighborhood)N4。其中混合邻域N1与链式邻域N2为主优化邻域,同时引入分割邻域N3和合并邻域N4以防止混合邻域N1与链式邻域N2陷入局部最优,这四种邻域互相补充,弥补其他邻域的不足,通过迭代优化逐步提升合乘方案的质量。DVNS-LTCPP(distributed variable neighborhood search for long-term carpooling problem)算法邻域的具体定义如下:
(1)混合邻域N1。混合邻域通过交换两个合乘小组中的用户达到降低两个合乘小组总出行成本的目的。首先计算合乘方案S中的所有合乘小组P的重心坐标(wx,wy),如式(21)所示。
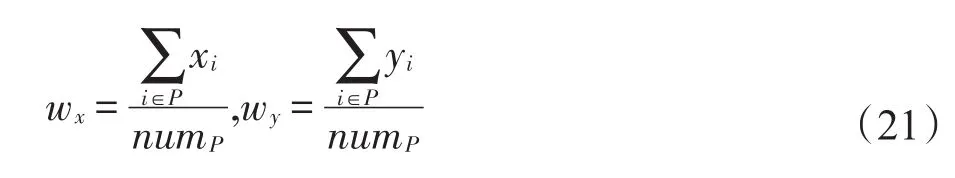
每次操作选取一个合乘小组P1,筛选出P1中距P1重心最远的用户i,然后计算该用户与P1重心的距离dP1i,最后计算P1与S中其余合乘小组重心的距离差wdP,如式(22)所示。在S中选出满足式(23)约束的合乘小组,并将这些合乘小组按照wdP值由小到大依次插入到合乘小组集合Stemp中。

对于Stemp中合乘小组与P1进行如下操作:
①选出Stemp中第一个合乘小组Pt1,并将该合乘小组从Stemp中删除。
②从P1与Pt1两个合乘小组的所有用户中筛选出距离最远的两个用户,将这两个用户作为两个新的合乘小组的司机,然后将P1与Pt1中其余用户按照Regret Insertion算法分配到两个新的合乘小组中。
③对新的合乘小组进行结果评估,若总出行成本降低,则对S进行更新,混合邻域搜索操作结束,否则继续执行步骤①直至Stemp为空集合。
混合邻域操作的示例图如图3所示。该操作的复杂度为O(n2)。
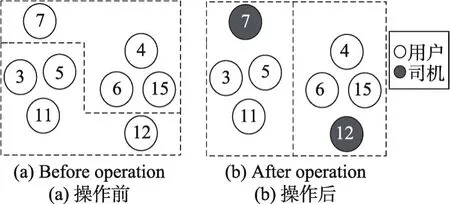
Fig.3 Example of mixed neighborhood图3 混合邻域示例图
(2)链式邻域N2。链式邻域将当前合乘小组中距离合乘小组重心较远的用户移动到距离当前合乘小组重心距离更近的其他合乘小组中,从而降低出行成本。链式邻域操作如下所示:
①构建一个合乘小组循环链表L存储合乘小组。
②首先从S中的每一个合乘小组P中筛选出距离该合乘小组重心最远的用户i,计算用户i与该合乘小组重心的距离dPi,然后计算用户i与S中其他合乘小组重心距离,其中diPx为这些重心距离值中最小的重心距离。最后计算dPi与diPx的差值disP,如式(24)所示。
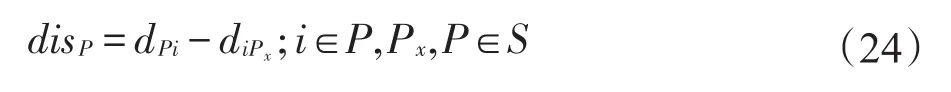
③在S中随机选择一个满足式(25)的合乘小组Pr作为L的第一个元素,并从S中删除Pr;如果S中没有满足式(25)的合乘小组,则链式邻域搜索结束。

④标记L中最近插入的合乘小组Pj,在S中筛选出与Pj重心距离差wd最小的合乘小组Pf,将Pf插入L中,并从S中删除Pf。
⑤重复步骤④直到S中所有的合乘小组全部插入到L中。
⑥以L中第一个合乘小组Pr作为起始点。将Pr中距离重心最远的用户移动到L中的下一节点的合乘小组Pnext中。
⑦如果下一节点的合乘小组违反了式(8)约束,则将该合乘小组中距离重心最远的用户移动到下一节点的合乘小组中。重复此操作直至操作节点的合乘小组满足车容量为止。
链式邻域的示例图如图4所示。该操作的复杂度为O(n2)。

Fig.4 Example of chain neighborhood图4 链式邻域示例图
(3)分割邻域N3。分割邻域将一个出行成本较高、用户间距离较远的合乘小组分割成多个合乘小组,使各合乘小组总出行成本降低。分割邻域每次可以将一个非独自驾车的合乘小组分为两个合乘小组。分割邻域首先对每一个非独自驾车的合乘小组计算该小组中所有用户的重心距离差之和sumP,如式(26)所示。
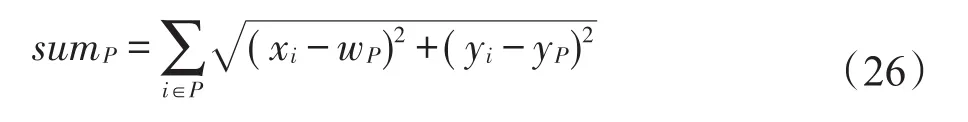
在sumP值最大的n个合乘小组中随机选出一个合乘小组进行分割操作。其中如果n设置得过大则容易导致随机性较强,算法收敛速度较慢;n设置过小,会导致该邻域操作的随机性下降,容易产生对某些无法成功分割的合乘小组进行重复分割的情况,致使计算效率下降。经过多次实验,将n设置为非独自驾车的合乘小组数量的1/4效果较好。然后将该合乘小组中互相之间距离最远的两个用户分到两个合乘小组中作为司机,其余用户按Regret Insertion算法分配到两个合乘小组中。分割邻域的示例图如图5所示。该操作的复杂度为O(n)。

Fig.5 Example of divide neighborhood图5 分割邻域示例图
(4)合并邻域N4。合并邻域将两个合乘小组合并成一个合乘小组从而降低出行成本。合并邻域操作每次可合并两个人数没有达到车容量约束的合乘小组,并且合并后的合乘小组满足式(8)的约束。其具体操作如下:
①构建一个合乘小组S1存储合乘小组集合S中人数未达到车容量的合乘小组。若S1中的合乘小组数量小于2,则合并邻域搜索结束。
②构建一个合乘小组链表l存储合乘小组,计算S1中各个合乘小组的车容量与实际搭载人数的差值difP,选出difP最大的合乘小组Pm存入l中,并从S1中删除合乘小组Pm。
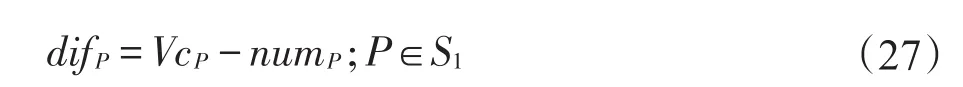
③计算S1中的各个合乘小组Pk重心与Pm重心之间的距离差wdPk,并将S1中各个合乘小组按wdPk
值由小到大依次存入到l中。
④将Pm与l中第二个合乘小组进行合并,如果合并后的合乘小组满足式(8)的约束,则合并邻域搜索结束;否则Pm与l中下一个节点的合乘小组进行合并,直至合并成功或与l中最后一个节点的合乘小组进行合并操作,合并邻域搜索结束。
合并邻域的示例图如图6所示。该操作的复杂度为O(n)。
4.2 结果评估
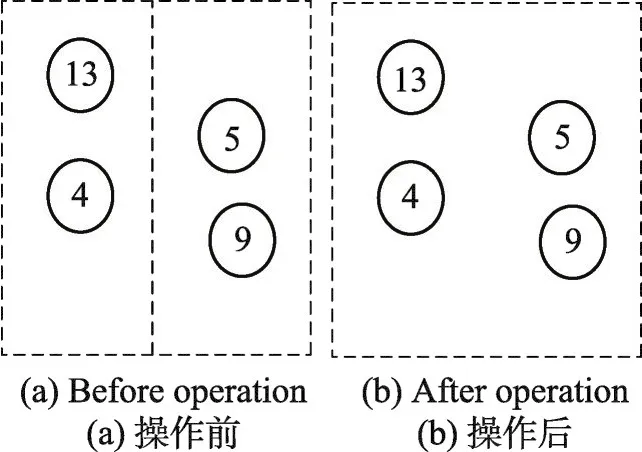
Fig.6 Example of merge neighborhood图6 合并邻域示例图
目标函数的评估通常是所有的启发式算法中最费时的操作。对于长期车辆合乘问题,一个完整的结果评估包括计算成本、验证每个合乘小组的车容量、司机行驶时间和时间窗口约束。由于邻域操作后的合乘方案S′与S仅部分合乘小组不同,本文提出了一种更有效的评估方法。该方法评估合乘方案中发生变化的合乘小组E(s,g),其中s是当前合乘方案,g是组内用户发生变化的合乘小组,而并非对S′中所有的合乘小组进行评估,因此极大地提升了评估效率。这种评估方法的复杂度与搜索过程中使用的邻域相关。其中混合、分割和合并邻域操作只对两个组内用户发生变化的合乘小组进行评估。对于链式邻域操作,组内用户发生变化的合乘小组数量不定。
在评估之前首先检查各合乘小组的行驶时间和时间窗约束,对于不满足行驶时间和时间窗口约束的合乘小组将通过与构建初始合乘方案中使用的相同修复过程进行修复。
4.3 VNS-LTCPP的主要结构
综上所述,VNS-LTCPP算法主要应用四种不同的邻域结构连续对合乘方案进行邻域搜索操作,并对各合乘小组进行行驶时间和时间窗约束验证与修复,最终得到优化后的合乘方案。VNS-LTCPP算法的整体结构介绍如下。
首先根据Regret Insertion算法构建初始合乘方案S0,并对S0中各合乘小组进行行驶时间和时间窗约束验证与修复得到S。然后对S进行迭代优化,每次迭代优化过程中所应用的邻域搜索依次为混合邻域N1、链式邻域N2、分割邻域N3和合并邻域N4。这四种邻域搜索依次对S进行邻域搜索操作,当前邻域搜索Nk对S进行邻域搜索操作后生成S′,VNS-LTCPP算法对S′中各合乘小组进行行驶时间和时间窗约束验证与修复得到S″。如果S″的总出行成本比S低,则将S″替代S,并对S进行下一次迭代优化;否则切换到下一个邻域搜索。当迭代次数超过规定次数n时,优化过程停止。

4.4 VNS-LTCPP分布式结构
4.4.1 Spark基本概念
Spark是一个分布式的内存计算框架,其特点是能处理大规模数据,计算速度快。Spark延续了Hadoop的MapReduce计算模型,相比之下Spark的计算过程保持在内存中,减少了硬盘读写,能够将多个操作进行合并后计算,因此提升了计算速度。同时Spark也提供了更丰富的计算API。
MapReduce是Spark的计算模型,其特点是Map和Reduce过程高度可并行化;过程间耦合度低,单个过程失败后可以重新计算,而不会导致整体失败;最重要的是数据处理中的计算逻辑可以很好地转换为Map和Reduce操作。
RDD(resilient distributed dataset)是Spark中最主要的数据结构,RDD是分布式的数据集,每个RDD都支持MapReduce类操作,经过MapReduce操作后会产生新的RDD,而不会修改原有RDD。RDD的数据集是分区的,因此可以把每个数据分区放到不同的分区上进行计算。
4.4.2 VNS-LTCPP算法分布式设计
VNS-LTCPP算法可以很好地应用于分布式系统,本文基于Spark平台将算法计算部分部署到多台计算机上进行并行化计算。Master节点负责构建初始合乘方案,为每个Worker节点调度任务,通过对比各Worker节点返回的优化合乘方案的总出行成本得到总出行成本最低的合乘方案;各Worker节点负责对初始合乘方案进行迭代优化。VNS-LTCPP算法分布式结构如图7所示。

Fig.7 VNS-LTCPPalgorithm distributed structure diagram图7 VNS-LTCPP算法分布式结构图
VNS-LTCPP算法并行化主要基于Spark的Map及Reduce操作来实现,首先Master节点按照初始合乘方案算法求解初始合乘方案,与集群管理器通信,通过集群管理器启动Worker节点。然后Master节点创建RDD存储合乘方案,并将RDD及Map、Reduce操作以任务的形式提交到各个Worker节点的执行器中。程序配置分区数为8,每个分区都存储一个完整的合乘方案数据,每个Worker节点启动一个执行器,每个执行器执行两个独立的分区任务,4台Worker节点一次可产生8个优化合乘方案。其中Map操作执行对合乘方案的迭代优化运算,经过规定迭代次数优化后得到优化合乘方案,Map操作产生新的RDD存储优化合乘方案。Reduce操作负责将Worker节点中每个任务所得的存储优化合乘方案的RDD返回Master节点。最后Master节点通过对Worker节点传回的优化合乘方案进行总出行成本计算,并筛选出总出行成本最低的优化合乘方案作为最终的车辆合乘方案。
为了减少通信时间的损耗,Master节点将任务传输给各个Worker节点中进行计算,每个Worker节点中的任务负责对合乘方案进行规定迭代次数的优化得到最终的优化合乘方案,任务完成迭代优化后通过Reduce操作将合乘方案传输回Master节点进行处理。
5 实验结果与分析
5.1 实验配置环境
Spark集群由一个主节点(Master)和四个从节点(Worker)组成,Spark版本为1.6.0。集群中各节点具体配置如表3所示。
5.2 实验数据及参数设置

Table 3 Cluster configuration表3 集群配置
实验所用算例由Solomon标准算例修改所得,算例的规模为100人(S1)、200人(S2)、400人(S3)和 1 000人(S4)四种规模。其中100人规模的算例有五组:S1_1,S1_2,S1_3,S1_4,S1_5;200人规模的算例有五组:S2_1,S2_2,S2_3,S2_4,S2_5;400人规模的算例有五组:S3_1,S3_2,S3_3,S3_4,S3_5;1 000人规模的算例有五组:S4_1,S4_2,S4_3,S4_4,S4_5。实验的参数设置:α=0.8,β=0.2,100人算例迭代次数为500次,200人算例迭代次数为1 000次,400人算例迭代次数为1 500次,1 000人算例迭代次数为3 000次。
5.3 实验结果分析
为验证VNS-LTCPP算法的收敛速度,本文对S1_1、S2_1、S3_1和S4_1进行实验计算,其中S1_1与S2_1的最低成本由Cplex平台计算得出,S3_1、S4_1由于算例规模较大通过Cplex平台无法在合理时间内计算出最低成本。实验对4个算例分别运行计算10次,并从每个算例10组实验结果中随机选取5组实验数据,实验结果如图8~图11所示。

Fig.8 Convergence diagram of S1_1图8 S1_1算例收敛图
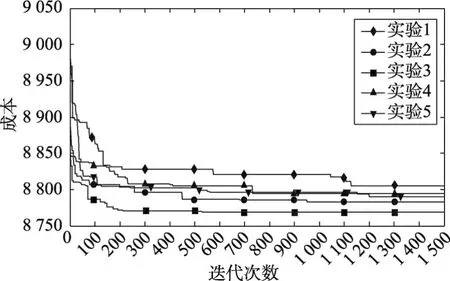
Fig.10 Convergence diagram of S3_1图10 S3_1算例收敛图

Fig.11 Convergence diagram of S4_1图11 S4_1算例收敛图
由图8~图11可以看出,VNS-LTCPP算法可以快速收敛,但实验的收敛速度随着算例的规模增大而减缓,实验结果的偏差也会随着算例规模的增大而变大。同时由于在构建初始合乘方案时,司机的选择具有随机性,因此在相同算例的各次实验中所得合乘方案均有所不同,造成了初始合乘方案的出行成本有所差异。对于生成质量较差的初始合乘方案同样可以得到很好的优化结果。由图8、图9可以看出VNS-LTCPP算法的收敛所得的最终成本也趋近于最低成本。
为了验证VNS-LTCPP算法的精度和可靠性,本文对100人规模和200人规模的算例进行实验,每个算例进行10次运行计算。其中Ropt表示算例的最低总出行成本,Rmin表示实验所得的最低总出行成本,Rave表示实验的平均总出行成本,AME表示实验的平均误差,ME表示实验的最小误差。实验结果如表4所示。

Table 4 Precision experimental test表4 精度实验测试
由表4可以看出,实验的平均误差为0.31%~0.65%,VNS-LTCPP算法具有很高的精度和可靠性,对于200人以内规模的算例可以得到质量可靠的合乘方案。
本文提出的基于分布式的复合变邻域算法由于分布式的算法设计和集群节点之间网络通信原因,理论上在相同实验环境下其整体计算时间要高于非分布式的计算时间,此外由于VNS-LTCPP算法具有随机性,会出现优化效果较差的优化合乘方案,而分布式计算可以有效地过滤掉较差的优化合乘方案,能够最大限度地得到成本更低的优化合乘方案。因此本文进行了分布式计算与非分布式计算之间的对比实验。分布式计算每台Worker节点一次计算出两个优化合乘方案,故分布式计算一次可以得到8个优化合乘方案并从中选取总出行成本最低的优化合乘方案。每个算例的分布式计算实验次数为10次,其中Rdis表示平均成本,Tdis表示平均计算时间。非分布式计算实验分为两组实验,其中实验1为一次计算出1个优化合乘方案,实验次数为8次,其中R1表示平均总出行成本;实验2为一次计算出8个优化合乘方案,实验次数为10次,其中T2表示平均计算时间,时间单位为ms。Per表示Tdis相对于T2节约的时间的百分比。具体数据如表5所示。
由表5可以看出VNS-LTCPP算法分布式计算的平均总出行成本Rdis整体上要低于实验1的平均总出行成本R1,其中1 000人算例的效果最为明显。在计算时间上,由于通信时间和任务调度时间的时间损耗对于100人和200人规模的算例,分布式计算的平均计算时间Tdis对于实验2的平均计算时间T2并没有明显减少,但随着算例规模和优化迭代次数的扩大,通信时间和任务调度时间所占的时间损耗比例逐步降低。400人和1 000人规模算例分布式计算所需时间明显低于实验2的平均计算时间,其中1 000人规模算例约为分布式计算的平均计算时间较实验2的平均计算时间节省60.6%~63.0%,因此对于大规模算例分布式计算的时间具有明显的优势。

Table 5 Distributed contrast experiment表5 分布式对比实验
从整体上看,对于100人、200人规模的算例VNS-LTCPP算法分布式计算的优势并不明显,但随着算例规模和迭代次数的增大VNS-LTCPP算法分布式计算在合乘方案优化和计算时间上的优势明显增强。因此VNS-LTCPP算法分布式计算可以更好地解决1 000人及更大规模算例的合乘方案优化问题。
6 结束语
本文构建了LTCPP的数学模型,提出了针对该问题的复合变邻域搜索算法,并将算法与分布式计算相结合。通过实验结果分析,VNS-LTCPP算法与分布式计算能够在短时间内求解出较高质量的车辆合乘方案,可以有效降低机动车出行数量,降低环境污染,节约出行成本,具有很高的实用性。此外,由于本文用户目的地相同,而在实际生活中用户群体的目的地不尽相同,因此在下一步研究中可将用户群体按目的地划分为多个用户群体,对多目的地的用户群体进行分布计算。经过实验观察,本文算法在构建初始合乘方案时,出行总成本还有很大的波动,将来的研究拟对初始合乘方案的构造进行完善。
