函数与导数压轴题中赋值确定参数范围后的处理策略

曹凤山, 朱伟义

(1.余杭区教育发展研究学院，浙江 杭州 311100； 2.浙江师范大学数学与计算机科学学院，浙江 金华321004)

函数与导数压轴题中确定参数范围是常见的问题形式.从“数学的原点”看，函数与导数试题中往往涉及一些特殊点(极值点、端点、零点等)，如果能充分利用这些点，通过赋值，得到参数的取值范围，往往可以优化问题求解.但赋值法只是确定范围的必要条件，不是充要条件，还要证明充分性，赋值得到的范围并不一定是问题的解，赋值后还有不少问题需要解决.本文结合具体案例，给出赋值后的一些处理策略，供读者参考.

1 赋值后得到参数单个值，然后证明充分性

如果可以判断某个点为极值点，那么可以利用函数取极值的必要条件建立关系式，求出参数值，然后证明充分性.极值点的判断要根据函数结构，如指数函数要关注“0”，对数函数关注“1”，代数形式需留意其零点等.

例1已知函数f(x)=ex-sinx-cosx，g(x)=ex+sinx+cosx.

2)若g(x)≥2+ax，求a.

(2021年“八省联考”数学试题第22题)

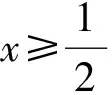
p(x)≤p(0)=1.

综上所述，f(x)≥0.

2)若g(x)≥2+ax，则

ex+sinx+cosx-2-ax≥0.

令h(x)=ex+sinx+cosx-2-ax,观察该函数的特点可知h(0)=0，又h(x)≥0，从而x=0是函数h(x)的一个极小值点.

由h′(x)=ex+cosx-sinx-a，得

h′(0)=2-a=0，

于是

a=2.

下面证明充分性.当a=2时，

h(x)=ex+sinx+cosx-2-2x，

从而

h″(x)=ex-cosx-sinx.

故h(x)=ex+sinx+cosx-2-2x≥0成立.

2 赋值后得到参数范围，化为单值检验问题

有些极值点或区间端点赋值后得到的不是参数的单个值，而是一个范围，要检验充分性很烦琐.若能转化为单值,则简单很多.

例2已知函数f(x)=aex-1-lnx+lna．

1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

2)若f(x)≥1，求a的取值范围．

(2020年全国高考数学山东卷理科试题第21题)

分析1)略.

2)取x=1，则a+lna≥1.令函数g(x)=x+lnx，因为g(x)单调递增，且

g(1)=1，

所以

a≥1.

关于a的函数h(a)=aex-1-lnx+lna是增函数，只要证明

h(1)=ex-1-lnx≥1，

即证

于是f(x)≥1，故a的取值范围为[1,+∞).

3 赋值得到参数值，然后逐步调整，再检验

有些赋值不是函数的极值点，也不是区间端点，赋值只能得到一个相对压缩的范围，检验时就需要十分仔细.

例3已知函数h(x)=(x2-2x)lnx-a(x2+2x)(其中a∈R).

1)若a为整数，且h(x)≥0在(0,+∞)上恒成立，求a的最大值；

(2021年浙江省新高考联盟数学联考试题第22题)

分析1)根据函数h(x)的特点，容易想到当x=1时,h(1)=-3a≥0，故a≤0.a=0是最大值吗？

当a=0时，h(x)=(x2-2x)lnx，当1

仔细分析可知：当a=0时，函数h(x)=(x2-2x)lnx，虽然在(0,+∞)上h(x)≥0不成立，但是只有当1

当a=-1时，

h(x)=(x2-2x)lnx+(x2+2x)

h(x)≥0.

综合以上讨论可知：当a=-1时，h(x)≥0.这里，先赋值然后根据具体情况微调，得到参数的值.

2)由题意可知

H′(x)=2[(x-1)lnx-a(x+1)]=0，

得

要证明x2>(2a+1)x1，只要证明

记g(x)=(x+1)2-2lnx(其中x>1)，则

故

g(x)>g(1)>0.

4 赋值后转换主元，再检验

赋值后若得到的是参数的取值范围，又不能转化为单值检验，则可以转换主元，看成参数的函数，从而完成充分性的证明.

(注：e=2.718 28…为自然对数的底数.)

(2019年浙江省数学高考试题第22题)

(1)

这里不能用区间端点证明.

式(1)左边可以看成关于x的函数，也可以看成关于a的函数.

也可以转化为

(2)

式(2)开口方向是确定的.我们选择式(2)作为研究对象，函数模型最熟悉，形式相对简单.

故

p(x)≥p(1)=0，

于是

由以上案例可以看出，赋值确实是求解一些函数与导数压轴题不错的选择，但是赋什么值、赋值后如何处理还是有不少值得探究的，不能一概而论、一赋了之.“回归数学原点”“回归问题原点”“具体问题具体分析”仍然是解题的不二法门.