一道高考试题的教学实践及思考

许家钊

(苏州大学附属中学，江苏 苏州 215000)

1 课题背景

高考方向：2020年10月，中共中央国务院《深化新时代教育评价改革总体方案》指出,稳步推进高考改革，构建引导学生德智体美劳全面发展的考试内容体系，改变相对固化的试题形式，增强试题开放性[1].2020年全国数学新高考Ⅰ卷第17题第一次出现了以三角为载体的结构不良问题，随后在2021年全国及部分省市的高考数学试题中不仅出现了以三角为载体，还出现了以数列、函数为载体的结构不良问题．可见数学高考改革的方向便是增加试题的开放性，因此在平时教学中增加开放性试题教学显得尤为重要．

教学目标：掌握解三角形的基本知识和基本方法；了解三角结构不良问题的常见类型并掌握相应的解决办法；在解决三角结构不良问题的过程中体会如何选择条件、如何解决问题、如何优化方法．

2 教学片段

片段1

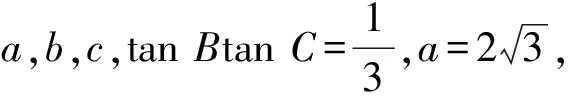
1)求角A,B,C的大小；

2)求△ABC的周长和面积．

学生答题情况：31名学生中，选①的有11名，选②的有20名，选②的学生多于选①的．

师：为什么想到选②？

生1：因为我发现它们都是正切．

师：生1从函数名的角度迅速做出选择，选择好之后如何处理？

师：你是怎么计算出这个结果的？

生1：利用消元法解方程组．

师：太棒了！

(生2举手，教师示意其回答.)

(全班学生自发鼓掌.)

师：生2看到了和与积，联想到了韦达定理．接下来，我们来研究选择①之后的解决方案．

两式相减，得

从而A=120°.

师：生3想到了切化弦，接下来你是如何求角B和C的呢？

师：生3的功底很扎实，太棒了！本题还有没有更优化的方法？

(1分钟后，生4举手，教师示意其回答.)

生4：将两式相加，得

cosBcosC+sinBsinC=cos(B-C)=1，

从而B=C=30°.

(全班响起一片掌声.)

师：从同学们的掌声中可以发现生4的方法很受欢迎，给出了本题的一个优化方案.请问你是怎么想到的呢？

生4：我看到生3将其相减得到角A，发现它们相加是特殊值．

师：生4的眼光独到，看到了特殊值，从而得到特殊角．

师(小结)：感谢以上几位同学，让我们通过例1经历了三角结构不良问题中如何选择、如何解决、如何优化的全过程．

教后反思本题在已知两个条件的基础上，进行“二选一”，条件聚焦于角B和角C，属于三角形中的“边角边”类型，重点在于解决第1)小题.从分析过程可以看出选②相对简便一些，从运算结果来看，属于“选择不同结果相同”的类型，对三角函数、切化弦思想、两角和与差的余弦公式以及辅助角公式的运用提出了很高的要求．

教师应在带领学生读题、分析试题类型、如何选择条件、如何优化解题方法等环节上舍得花时间．在本题解决之后的二次做题环节中，还应带领学生分析本题在揭开神秘面纱之后，究竟是一个什么样的解三角形问题.本题的最终落脚点还是在于解三角形的基本模型，教师除了注重三角基本知识、基本方法的教学与训练外，还应总结“两角一边”“边角边”“边边角”“三边”等这些常见的知三求三模型，熟练掌握正弦定理和余弦定理的使用类型，才能使学生在日后顺利地解决此类问题．

片段2

注：如果选择多个条件分别解答，按第一个解答计分．

(2020年全国数学新高考Ⅰ卷第17题)

学生答题情况：31名学生中，选①的有11名，选②的有5名，选③的有15名.

师：我很好奇，为什么选③的同学明显多于其他？

师：生5同时使用了题设中的一个条件和所选的结论，得出了三角形3条边的比例关系，从而得出与题设中另一个条件矛盾，确定此种情况下三角形不存在，可谓是迅速．

师：生6同时使用题设中两个条件和所选的结论，得出了三角形的3个角度，这时发现与题设条件矛盾，从而三角形不存在．生5和生6选择的条件相同，但后面得出矛盾的方法有所区别，都很不错．

(教室里再一次响起掌声.)

师：选①的同学是怎么处理的呢？

(全班再一次不约而同地鼓掌.)

师(小结)：通过例2我们发现，先选择再分析，或者先分析再选择，都是很好的处理方法.高考题留给我们的思考空间很大.

教后反思本题有如下3个特点：1)试题只有一问；2)在已知两个条件的基础上，进行“三选一”，3个备选条件较为分散，有边边关系、也有边角关系，有乘积关系、也有倍数关系，这些特征直接影响到选择之后的解决办法；3)本题属于“选择不同结果不同”类型.

学生既可以先分析两个已知条件，得出三角形3条边长的关系，从而确定三角形的形状，也可以根据已知条件中的一个以及选择的条件，分析出相应的结果，从而发现矛盾．解决的方向和角度很多，是开放度较高的一道试题．

片段3

1)求B的大小；

2)在以下3个条件中选择一个作为已知，使△ABC存在且唯一确定，并求边BC上的中线的长度．

(2021年北京市数学高考试题第16题)

学生答题情况:31名学生中，选②的有21名，选③的有10名，全班都正确．

生8简述答题过程：

1)A=B=30°，C=120°.

2)若选①，则无法确定三角形，故不可以选①.

3 教学反思

反思1例1主要考查了三角函数同角基本关系式，两角和与差的余弦公式，从学生的答题情况来看，学生正向思维已经比较熟练，但是关于两角和与差的余弦公式的逆用明显不熟悉，教学中应予以重视．另外，两数的和与积在韦达定理、两角和的正切、基本不等式中经常出现，教师应在平时的教学中给予梳理与总结．例1代表的是“条件部分缺失，结论一致型”，但重心却落在了选择之后如何处理上，开放度不够高，与高考命题方向有一定的差距，不够典型．

反思2例2是一道高考题，开放度之高可想而知，学生思考的角度较多，具有很强的时代特征，与高考命题改革的方向契合度很高．笔者在课堂教学中发现基于“先分析再选择”的学生只有2名，绝大多数学生都是“先选择再分析”，也涌现了一批好的解决方法，这点值得夸赞．两种思路有很大的差异性，在此类问题的教学中到底该倾向于哪一个，仍是一个值得商榷的问题.笔者认为应侧重“先分析再选择”的做法，希望得到同行专家的指点与建议．

反思4高三的教学往往是通过一轮复习和二轮复习展开的，其中试题评讲课占了很大的比重，教师对于试题如何评讲，以及指导学生如何答题显得尤为重要.但是笔者认为，还有一个环节也很重要，那就是对于优秀试题的“二次做题”，甚至是“三次做题”，它不同于试题订正，也不同于错题整理，它是在学生已经掌握了某类问题的常见模型以及相应的解题方法之后，对于该类型的优秀试题的再做再认识，笔者在实践的过程中，发现该方法对于提升学生的数学答题水平有较好的效果．

4 结语

2019年11月，教育部考试中心发布了《中国高考评价体系》，是深化新时代高考改革的理论支撑和实践指南，是统筹推进高考综合改革和高中育人方式改革的重要载体[1]．2020年10月，中共中央、国务院印发的《深化新时代教育评价改革总体方案》明确指出，要“改变相对固化的试题形式，增强试题开放性，减少死记硬背和‘机械刷题’现象”．近几年的数学高考命题已经从能力立意转变为价值引领、素养导向、能力为重、知识为基、试题形式进行了调整，部分试题的答案与结论也没有一尺之规．结构不良问题正是基于以上背景的一种尝试．

笔者在此次参加市级公开课的活动中，经历了研究高考、查找资料、构思打磨、向同行请教、优化等一系列环节，提升了自己对三角结构不良问题的理解，进一步激发了研究热情．笔者还体会到：在课堂教学中，教师应舍得花时间让学生思考，多多创造学生之间学习与碰撞的机会，教师还应及时给予表扬及夸赞，如此才可以树立学生的主体地位，激发学生的课堂参与热情，从而提升教学效果．