一类二次型递推数列中的“倒数法”——从2022年浙江卷第10题说起

熊焕焕， 顾予恒

(杭州第二中学钱江学校,浙江 杭州 311215)

2022年的高考大幕已经落下，浙江省数学高考试题(以下简称浙江卷)这一座大山依然压着考生们喘不过气来,它仍然保持着高难度、高计算量的特点.在近几年的浙江省数学高考中，数列一直作为选择题压轴,可见数列的地位在浙江卷中不可撼动.2022年浙江卷第10题以一类特殊的二次型递推数列为背景,考查了数列的放缩.本文着重从这一类特殊的数列出发,探索求解此类问题的通性通法.

1 回归课本，不忘初心

笔者翻阅了人教A版高中《数学(必修2)》发现，教材着重强调等差(等比)数列的概念、通项公式以及求和公式.粗粗一看，本题和课本内容几乎没有关联，实则不然，它们之间内有乾坤.下面进行详细阐述.

一般地，累加法适用于形如an+1-an=f(n)的数列问题，其中式子左边的次数都是一次，且结构又是差型，右式是可相加的.

2 寻找本质，追根溯源

方法1(直接取倒数)

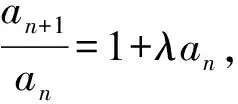
3 细品高考，真题分析

( )

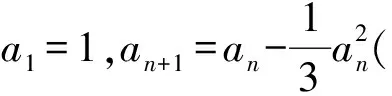
(2022年浙江省数学高考试题第10题)

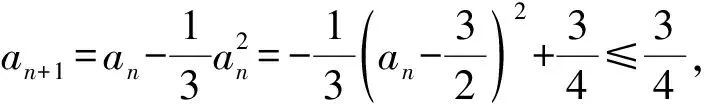
一方面，因为

累加得

从而

于是

另一方面，因为

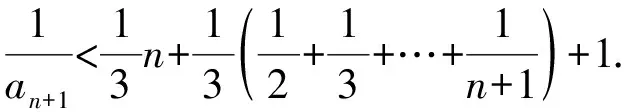
又

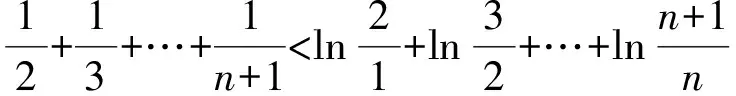
=ln(n+1),

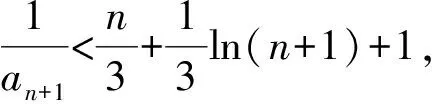
于是

评注本题是一道考查一类特殊的二次递推型通项放缩的好题，需要学生对数列的概念、单调性与递推关系等基础知识都了解，考查数学抽象、数学运算与逻辑推理等素养.本题通过“倒数法”把原式变形为倒数齐次式，然后利用累加法进行放缩.

4 例题研究，深入剖析

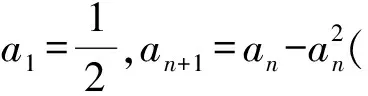
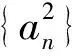
(2015年浙江省数学高考理科试题第20题)

1)证明利用方法1，直接取倒数，化简得

利用方法2,相除取倒数,化简得

因此

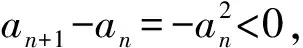
且

从而

an>0,

于是

故

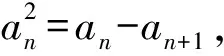
Sn=a1-an+1.

即

代入得

评注我们惊讶地发现例1与例2高度相似.师生不应该只停留于做题，而应从做这一题看到其背后的一类题，总结归纳这一系列题目的核心思想方法.

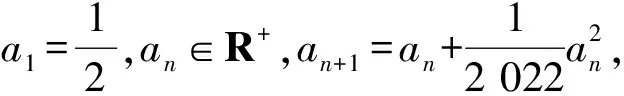
解根据方法1,直接取倒数,得

累加可得

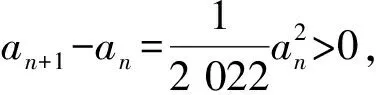
评注由例2和例3可以发现：两种方法虽然殊途同归，但是在解决具体题目时还应该具体分析.对例2来说，方法2较为简单；对于例3，方法1会更为快捷，因此遇到各类题目应采用不同的策略，从而使得解题效率达到最高.

5 潜心钻研，栎阳雨金

笔者认为对于复杂的高考题也应该追根溯源，不忘初心，回归教材.针对这一类特殊的二次递推型数列，我们只需要真正了解累加模型的结构特征，针对不同的题目应用与之对应的方法，对其累加之后,进行合理放缩就可以快速解决这一类问题.