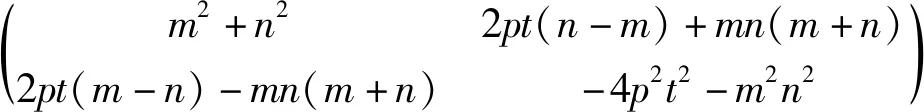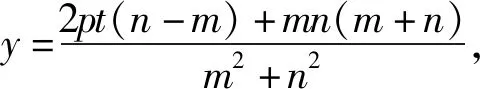与抛物线相关的一个定点问题
2022-08-09重庆市铜梁二中402560
中学数学研究(江西) 2022年8期
重庆市铜梁二中 (402560) 李 波 田 飞
圆锥曲线的定点问题中有很多有趣的结论. 笔者发现一个抛物线特有的定点问题,兹介绍如下:
性质如图1,A(-t,m),B(t,n)分别是直线x=-t,x=t(>0)上的定点,M是抛物线C:y2=2px(p>0)上的动点,直线AM,BM分别与抛物线C交于E,F(E,F存在且不重合),则
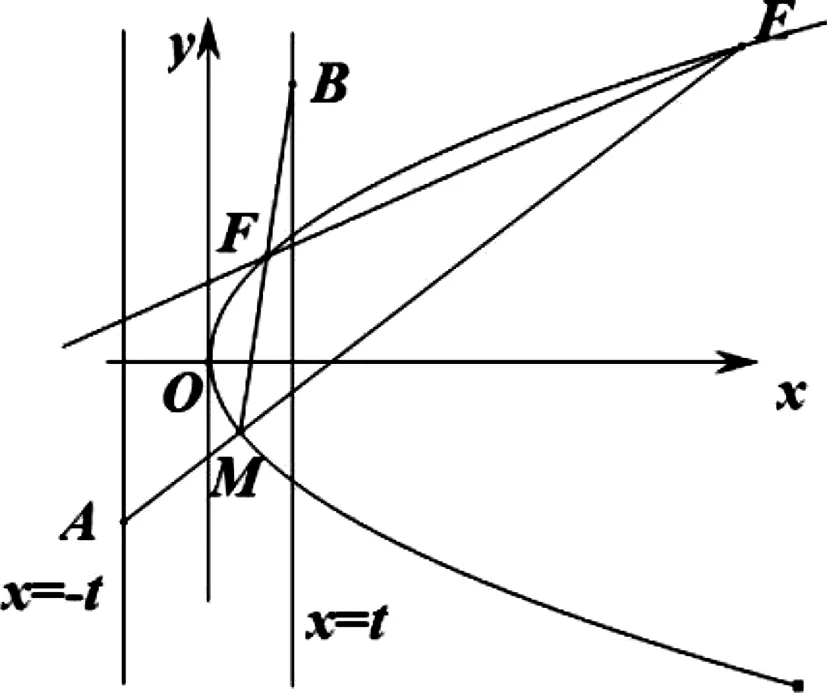
图1
(1)当m=n=0时,EF是垂直于x轴的动直线;
(2)当m,n中仅有一个为零时,EF恒过定点;
(3)当m,n均非零时,EF恒过定点当且仅当m2n2=4p2t2+2pt(m2-n2).
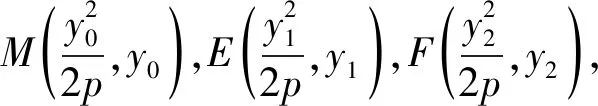

把①式左端看成关于y0的多项式,由于y0具有任意性,可得方程组

若直线EF过定点,即方程组②有唯一解.
为叙述方便,下面采用线性方程组理论来分析②的解的情况. 非齐次线性方程组②的增广矩阵
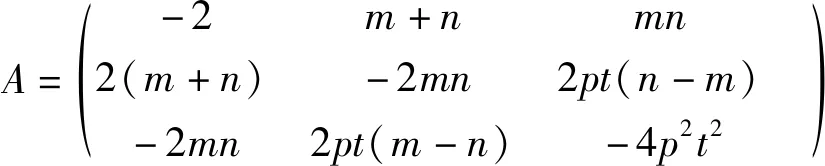
方程组②有唯一解的充要条件是增广矩阵与系数矩阵的秩都为2,且矩阵的初等行变换不改变矩阵的秩,则m2+n2≠0(即m,n不全为零)且矩阵