基于问题驱动的拓展课设计——以“反比例函数图象和性质”为例

浙江省宁波市海曙区集士港镇中学 (315171) 张 丹

《义务教育数学课程标准》(2011年版)的“综合与实践”是以问题为载体，培养学生问题意识、应用意识和创新意识的学习活动.浙教版教材是通过设置“探究活动”、“设计题”和“课题学习”等选学材料来体现.但是，多数教师对教材中这些材料处理一般是“视而不见”，或让学生“自主学习”，因此很少有学生去花时间研究在教师看来“毫无意义”的学习内容.事实上，这些材料在教材中不是可有可无的，它有助于学生学习能力和数学素养的提升，是教材内容的重要组成部分〔1〕.对于教材中选学内容教学，教师可以采用拓展课的形式，促进学生深度学习：即在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的学习过程〔2〕.本文笔者从浙教版《数学》八年级下的一道“设计题”出发，整合三角形、四边形等相关知识，开展了一节“反比例函数图象和性质”的拓展课，现把执教过程与思考予以展示，与同仁分享.

一、目标设定

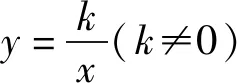
基于学情分析与设计题的表述，笔者设定以下的教学目标：

(1)学生通过经历观察、猜测、验证和证明的全过程，理解反比例函数的图象关于y=x和y=-x成轴对称的性质，及双曲线中直线运动产生的线段保持等量关系的性质.

(2)学生通过一系列问题解决，培养自身的数学思维、问题意识和创新意识.

(3)学生通过教师引领、独立思考和合作交流，进一步提升自身的几何直观、逻辑推理和模型思想等数学素养.

二、教学过程

1．呈现问题，激发兴趣

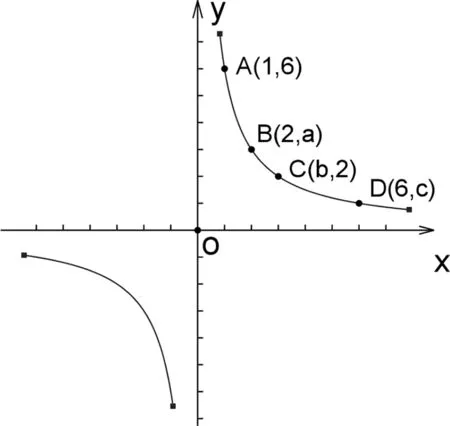
图1

(1)求k的值；

(2)求a,b,c的值；

(3)求点D关于原点O的对称点坐标.

2.深化问题，探索性质

师：从问题1解决中，我们可以看到，关于坐标原点成中心对称的两点坐标间关系是“对称点的横、纵坐标是互为相反数”，我们继续探索以下问题.

问题2 观察上题中A,B,C,D各点的坐标特征，回答下面问题：

(2)从图形直观上来看，点A与点D，点B与点C，点P与点Q是否关于同一条直线对称？

生1：A坐标为(1,6)，D坐标为(6,1)，B坐标为(2,3)与C坐标为(3,2)，可见A与D，B与C的坐标关系是“横、纵坐标互换位置”.

生3：点A与点D，点B与点C，点P与点Q都关于第一、三象限的角平分线对称.

师：它们都关于第一、三象限的角平分线对称，即关于y=x对称，那么，怎样证明“点P(a,b)和Q(b,a)关于直线y=x对称”呢？

学生陷入沉思之中，很多学生处于惘然.略待片刻，教师缓缓提示：以前我们是怎样证明“点(a,b)和点(-a,-b)关于原点成对称”？

生4：如图2，不妨设a,b都大于0，分别过点P、Q作PN⊥X轴，QM⊥Y轴,垂足为别为N、M.则OM=ON=b,QM=PN=a,∠PNO=∠QMO=90°,所以⊿PNO≌⊿QMO,于是，OQ=OP,∠QOM=∠PON,故∠QOG=∠POG,即PQ被直线y=x垂直平分，所以点P(a,b)和Q(b,a)关于直线y=x对称.

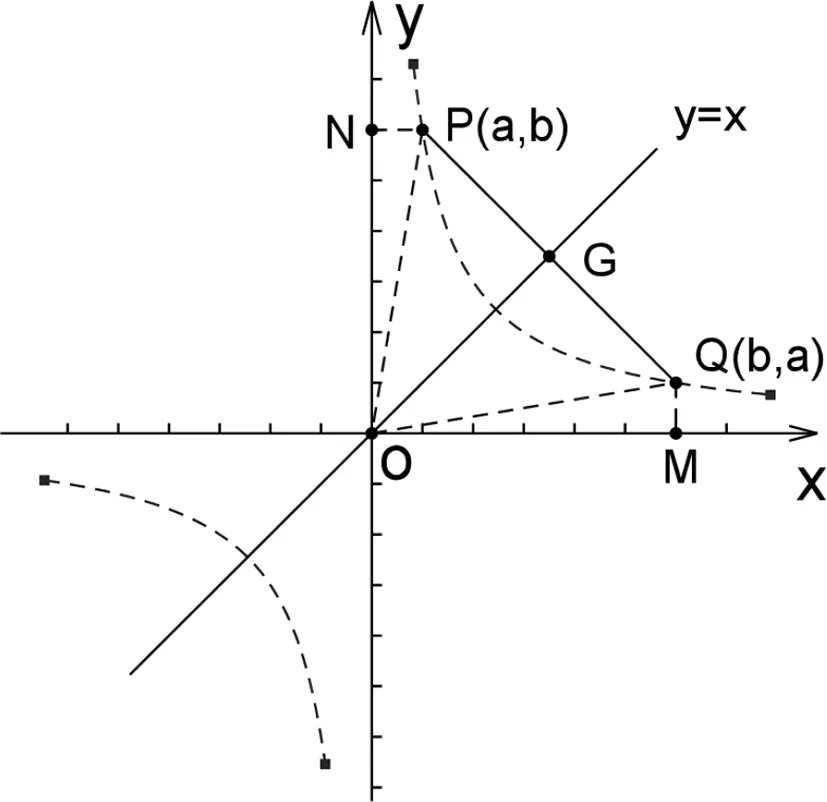
图2

师：漂亮﹗生4完美证明了双曲线关于直线y=x成轴对称图形.那么，双曲线除了直线y=x是对称轴以外，还有没有其他的对称轴？

刚进入兴奋状态的学生，一下懵住了，过了片刻，生5起来回答.

生5：老师，另一条对称轴会不会是第二、四象限的角平分线y=-x？

师：你猜得太对了，双曲线与以前学习过的矩形、菱形一样，有2条互相垂直的对称轴.它的证明过程与生4叙述的过程类似.具体的证明，请同学们回去自己研究.

设计意图：教师从学生已有的关于坐标原点对称点的坐标规律出发，让学生研究A(1,6)与D(6,1)、B(2,3)与C(3,2)、P(a,b)与Q(b,a)的坐标关系，发展学生数据分析观念；再借助图形直观，让学生直观感受双曲线的轴对称性，培养学生的几何直观素养；让学生经历观察、猜测、验证和证明的学习活动全过程，既提升了学生逻辑推理数学素养，又积累了活动经验.

3.拓展问题，应用性质

师：双曲线既是一个以原点为对称中心的中心对称图形，又是一个2条对称轴互相垂直的轴对称图形.这个性质与以前学习过的矩形、菱形的对称性比较类似，下面我们继续探讨以下问题.

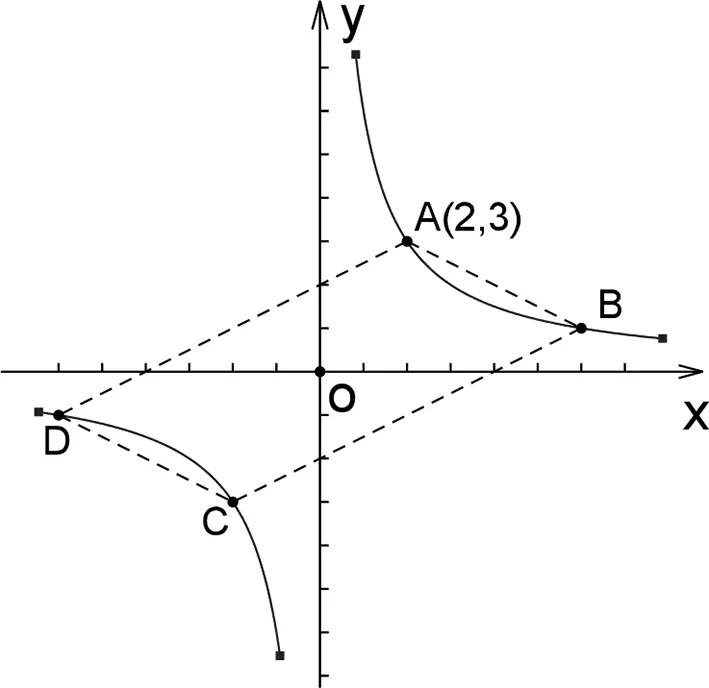
图3

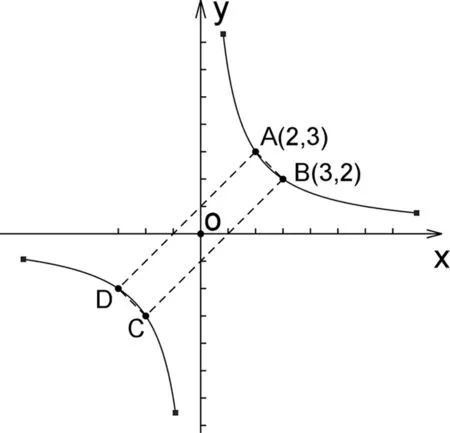
图4

师：真的吗？你能否给我们说一下“双曲线中不存在菱形”的理由.

生7：因为菱形的四个顶点都在2条对称轴上，而双曲线中有1条对称轴y=-x是在第二、四象限，所以它不可能与双曲线有任何交点.

师：说得真好﹗在图4的矩形ABCD中，隐去矩形的三边BC、CD、DA，作直线AB与坐标轴交于两点，得到问题3.

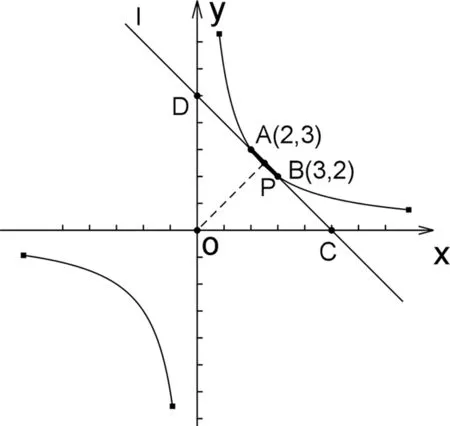
图5

生8：取AB的中点P,联接OP，则OP所在的直线为y=x.由于AB⊥直线y=x，易得△OPD、△OPC是等腰直角三角形，于是PD=OP=PC,所以AD=BC.

生9：点P既是AB的中点，也是CD的中点.

教师操作几何画板，把直线l绕着点A旋转，让学生探讨问题4.

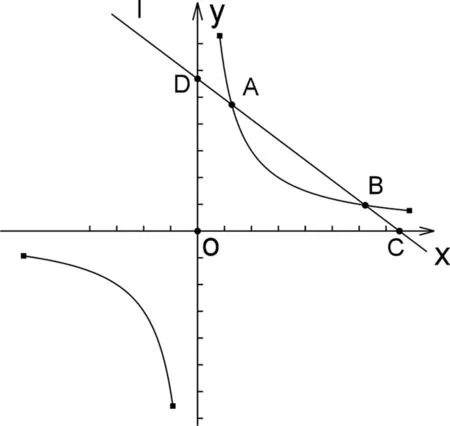
图6

于是，很多学生画图、测量、讨论，也有几个学生在静静地思考之中，过了一会儿，有一位学生起来回答.

生10：我一开始就想，会不会尽管直线l绕点A在旋转，而AD=BC的数量关系没有变化呢？画图测量之后，结果的确如此.

教师利用几何画板的测量工具，进一步验证生10猜想的正确性.

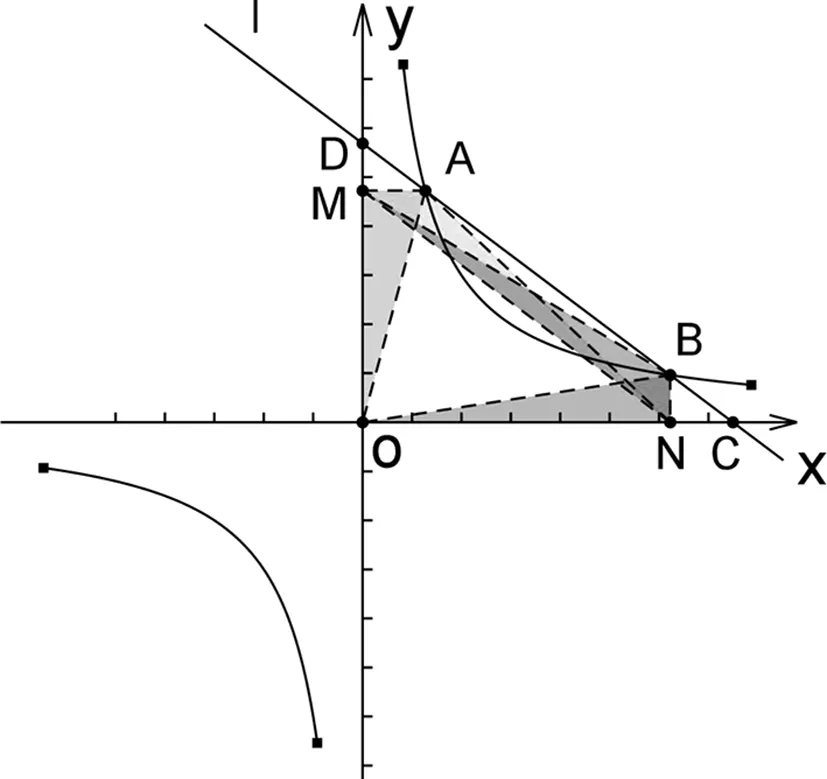
图7

师：证明两线段相等，常用全等三角形方法，那么怎样构造两个三角形呢？

生众：过点A、B分别作y轴、x轴的垂线，垂足分别为M、N.显然∠AMD=∠BNC，∠MAD=∠BCN.还差一个边相等条件，比如AM=CN.

师：在图7中，已有AM∥CN，欲证AM=CN，联接MN，则只需证四边形ACNM是平行四边形，那么这该如何证明呢？

在新课程标准下，课堂以“学生为中心”的教学理念，更加体现了历史学融入语文课堂的必要性。历史学的融入让语文课本的人文性更加生动风趣，让学生愿意去接受和理解原本晦涩难懂的语言和文字，激发了学生的学习兴趣，由原先“要我学”的教学模式变成了“我要学”的课堂模式，从而真正实现“以生为本”的课堂模式，实现素质教育。

生众：只要证明AC∥MN，考虑到反比例函数k的几何意义，应该用面积方法去证明.

生11：如图7，联接OA、OB、BM、AN.因为AM∥x轴，所以S△OAM=S△NAM，同理S⊿OBN=S⊿MBN，由于S⊿OAM=S⊿OBN=k，故S⊿NAM=S⊿MBN，所以AB∥MN.于是，四边形ACNM是平行四边形，所以AM=CN，易证⊿AMD≌⊿CNB，所以AD=BC.

师(惊喜)：很好，生12用解析法证明AB、CD的中点重合，从而说明AD=BC，是个好方法.我们继续探讨下面问题.

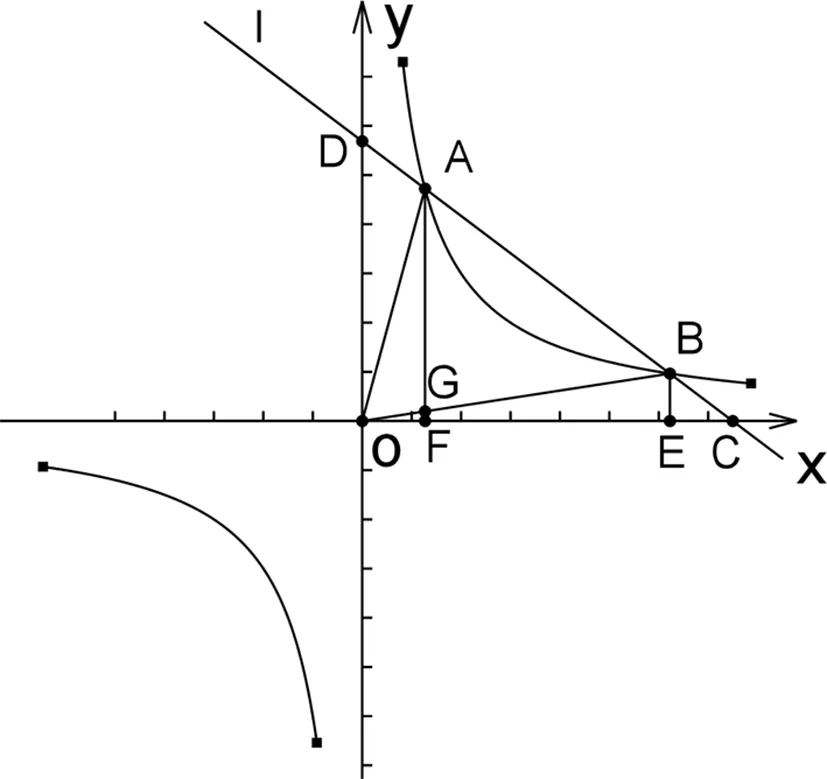
图8

(1)请探究OF与CE的数量关系；

(2)联接OA、OB，请探究⊿AOB与直角梯形AFEB的面积关系.

设计意图：本教学片段是让学生从双曲线的对称性联想到平行四边形、矩形、菱形和正方形的对称性，然后“从特殊到一般”探讨直线与双曲线、坐标轴的交点构成线段的数量关系，最后让学生研究“原点三角形”与直角梯形面积关系.笔者遵循“从简单到复杂”、“从特殊到一般”规律设置问题序列，旨在通过学生自主探究、合作交流和师生互动的方式，积累活动经验、展现思考过程、培养创新意识.

4.解决问题，提升素养

图9

例2 如图10，过原点的直线与反比例函数y=的图象交于A、B两点，点A在第一象限，点C在x轴正半轴上，连接AC交反比例函数图象于点D.AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连接DE.若AC=3DC，⊿ADE的面积为8，求k的值.(2019年宁波中考第18题)

图10

设计意图：例1与例2是问题6结论的两个应用，解决例2需要学生综合运用几何和代数两大内容领域的知识.设计这两个例题是为了培养学生的“数学建模”素养、“转化与化归”思想及综合运用知识解决问题能力，而培养学生数学素养、数学思想和应用意识应该是数学拓展课的首要目标.

5.反思小结，分享成果

围绕以下问题进行反思：本课的研究过程是怎样的？有哪些研究方法？

通过反思，让学生主动把双曲线对称性与矩形对称性进行类比，在探索过程中体会数学中“变”与“不变”的关系，领悟研究数学从“简单到复杂”、从“特殊到一般”思维方法.

设计意图：通过反思小结，让学生感悟知识间的联系，优化知识结构和体系；掌握数学研究方法，不断积累学习活动经验.

三、几点思考

教师要开展拓展课教学，应该做好以下三个方面的工作.

1.关注学生现实，促进深度学习

在本课中，笔者是从学生已有知识“双曲线中心对称性”出发，围绕“双曲线对称性”主题，让学生经历探究“双曲线的轴对称性”、“双曲线中的四边形”、“双曲线中直线运动产生的线段保持等量关系”等问题过程.在探究过程中，有画图、测量、猜测和验证等学生动手操作和自主探索过程；有师生合作交流中互相质疑、释疑和解疑的过程；在学生迷惑时，几何画板介入给学生探究提供几何直观支持的过程.

2.凸显数学本质，设置阶梯问题

在本课中，笔者以问题为引领，从易到难依次设计6个阶梯问题.问题从“双曲线的轴对称”、“双曲线中的四边形”、“双曲线中的相等线段”最后到“原点三角形与直角梯形面积相等”，解决问题所需的知识和思维层层递进，让不同层次的学生都获得成功的体验.

3.提升数学素养，培养应用意识

在本课中，笔者依次设置问题3、问题4与问题5的三个问题，让学生在探究中经历了两次从“特殊到一般”过程，培育学生的数学抽象素养；在问题4探究中借助几何画板验证，培育学生的几何直觉素养；在问题5证明中的“几何综合”证明和“代数解析”证明，培育学生逻辑推理.本课最后2个例题的解决，是利用问题6的结果作为数学模型，旨在通过问题解决培养学生的应用意识.