数学解题教学需从“就法论法”走向“以法生法”——由一节高三复习课引发的思考

江苏省南京市金陵中学河西分校 (210019) 杨 红

高三复习课阶段，解题教学就成为了课堂教学的“主旋律”.解题教学不能“就题论题”，而是要做到“归一类、得一法、通一片”，但现实教学中，不少教师的教学有避免“就题论题”现象的想法，但“就法论法”的现象依然明显.笔者最近听了一节高三复习课，深有感触.

1 教学过程简介

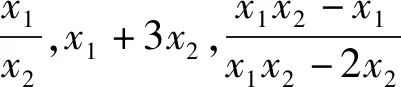
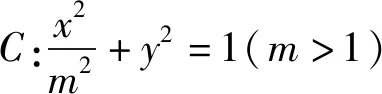
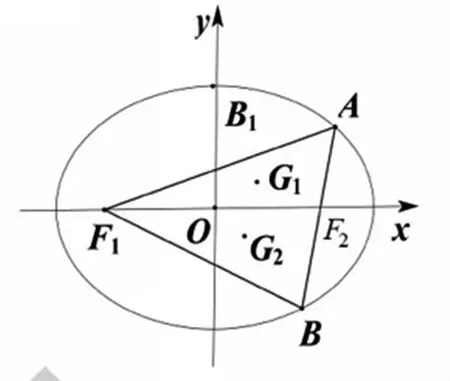
图1

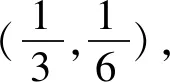
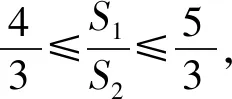
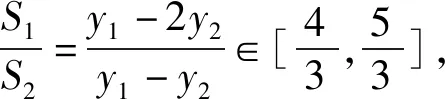
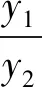
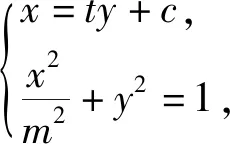
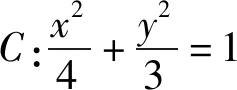
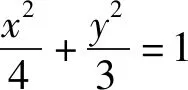
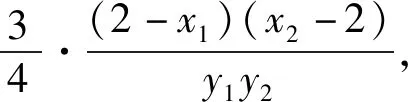
讲完两道例题后，接下去就是课堂练习，至此，本节课就结束了.纵观整节课，虽然涉及的方法比较巧妙，但自始至终都是教师在讲，学生没有独立思考的时间，完全是在“记忆、模仿”解题的结论和方法.

2 “就法论法”是一种急功近利的表现

课后，笔者就这节课的“师生互动”问题和上课教师进行了交流.上课教师给出的解释是：经过二轮复习，学生已经掌握了相当多的解题技巧，因此，教师只要把方法告诉学生，学生就能够理解与掌握，没必要再花时间在“师生互动”上；再说本节课的方法比较巧妙，学生自己很难想到，直接把方法呈现出来，能够提升教学效率.教师给出的解释听起来似乎有些道理，但仔细分析后，不难发现，这是一种“急功近利”表现，与学生的认知规律不相符.

2.1 “就法论法”以灌输现成结论为目标

现在关于解题方法研究的成果很多.因此，“拿来主义”就成了很多教师的不二选择，见到比较巧妙的解题方法，就直接照搬过来.由于好的方法实在太多，但教学时间有限，于是以“灌输”代替生成，以强化训练代替内化，就成为了高三解题教学的一种比较普遍现象.

本节课中“非对称韦达定理”的应用技巧在圆锥曲线的运算中确实能起到化繁为简的功效，但教师显然“太急”，学生还没理解题意，就给出了解题的过程，就把问题聚焦在对于目标函数的简化上，使得教学过程被解题方法所“绑架”，纯粹是为了灌输方法而呈现方法，造成了方法与问题的分析、问题的解决过程相脱节.其实，教学的重心首先应该放在对解题思路的剖析上，自然得到目标函数后，再引导学生思考如何对目标函数进行化简，这才是解题教学的正常流程.

2.2 “就法论法”无视方法之间的联系

学生知识的获得并不是靠教师的灌输，而是在已有认知经验下的意义建构，解题方法的获得也是如此，它也是在学生已有解题经验下的意义建构，但“就法论法”显然忽视这一真相.“非对称韦达定理”根基就是“韦达定理”，当遇到“非对称”结构时，韦达定理虽然不能直接套用，但并不一定非要把“非对称”化为“对称”不可，直接运用“求根公式”把坐标表示出来也能解决问题，而用坐标直接表示属于通性通法的范畴，是学生能够想到的方法.在此基础上，教师再引导学生思考如何对方法进行优化，从而自然引出如何把“非对称”化为“对称”，这样通性通法与“巧法”之间就建立了联系，学生也更容易理解数学方法的精髓了.

3 从“就法论法”走向“以法生法”

数学解题教学的真正目的并不是直接传授新的方法，而是在通性通法的基础上，通过思维的迁移，进一步优化生成更多“新”的方法.也就是说，解题教学的重心应该从“就法论法”向“以法生法”转变，从而使得解题方法前后关联，联系紧密，形成完整的思维脉络.下面以例2为例，谈谈具体的操作.

3.1 立足已有方法

3.2 生成创新解法

除了“消参”外，还可利用一些圆锥曲线的性质，实现“优法”.

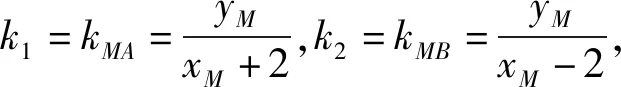
图2

总之，数学解题方法并不是空穴来风，也不是无源之水无本之木，而是立足学生的已有经验；数学解题教学也不是“灌输”，而是靠学生主动的意义建构.解题教学不能被眼花缭乱的方法所左右，而是要透过方法看清背后的数学本质.