深度学习的实践探究——以“以退为进”问题求解为例

江苏省苏州湾实验初级中学 (215200) 吴明飞

深度学习的研究起源于国外，Ference Marton和Reger Saljo于1976年首次公开提出深度学习(Deep Learning)这个概念，后来得到了更为深入、广泛的研究.随着核心素养概念的提出，深度学习的概念又一次被广大教师所谈及，深度学习得到了广泛的认同，并被不少人认为深度学习是培养核心素养的有效途径.深度学习一定具有思维深度，孙智昌等人指出，深度学习的“深度”应当具有“理解”和“创新”的方向[1],数学学习最强调就是理解学习，创新也是深度学习的一种表现.今天我们就从问题的解决过程中，体现创新的过程，了解深度学习的一些具体表现.

数学家华罗庚曾说过：“善于退，足够的退，退到最原始而不失去重要的地方，是学好数学的一个诀窍”.在解题的过程中，有时感到“进”有困难，没有思路，没有角度去“进”，可能是因为太关注目标，离题目“太近”，以致于管中窥豹，不能观其全貌，退一步海阔天空.我们不妨运用“退”的思路，“退”到我们最容易看清楚的地方，从而寻求突破口，再“进”上去.根据不同的问题，可以从一般退到特殊，从数退到形，从条件退到结论，从整体退到局部，从充要条件退到必要条件等等，退到一个我们更容易解决的问题上，找到思路，解决问题，并能够培养更高阶的思维.本文结合具体问题，谈谈这种策略的应用.

一、从一般退到特殊

当探寻一般性规律受阻时，往往可以通过特殊去探寻一般情形，即从一般退到特殊[2]这一策略，探寻解题思路.

例1 已知数列{an}中，a1=2，∀p,q∈N*，有ap+q=ap+aq，求数列{an}的通项公式.

分析1：由ap+q=ap+aq很难求出{an}的通项公式，可以先写出前几项，寻找规律，再求{an}的通项公式，实际上就是采用特殊化的方法，利用数学归纳法求出通项公式.

分析2：∀p,q∈N*，有ap+q=ap+aq，用特殊化的方法转化为常见的递推关系，即令p=n,q=1，得到an+1=an+a1.

解：令p=n,q=1，得到an+1-an=2，所以{an}为等差数列，an=2n，检验：∀p,q∈N*，有ap+q=2(p+q)=2p+2q=ap+aq满足.

本题采用从一般退到特殊，再由特殊推出一般规律，但要反过来检验一般性.

二、从数退到形

数属于数学抽象思维的范畴，形属于数学形象思维的范畴.抽象的东西很难把握，但形象的东西更容易解决，从数退到形，开拓解题思路，提高解题能力.

例2 设x,y,z∈(0,1)，求证：x(1-y)+y(1-z)+z(1-x)<1.

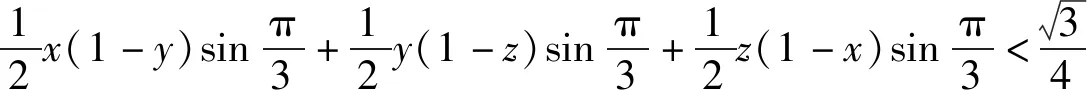
图1

三、从条件退到目标

有些题目，从已知条件去推出结论是很困难的，有时，我们可以先从目标出发，寻求所需条件，反而可以简化运算，达到意想不到的效果.

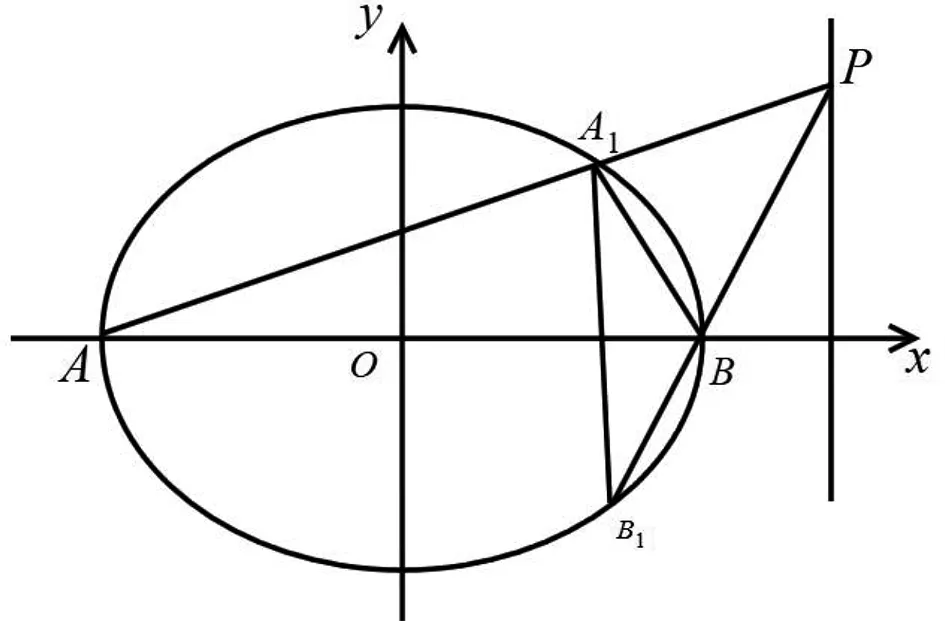
图2

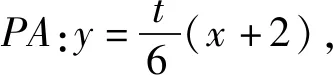
四、从整体退到局部

通常判断整体的性质不便解决，可以先研究其局部，局部的解决，往往伴随着整体问题的解决.

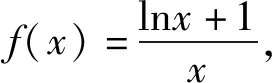
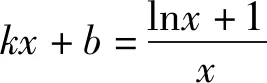
下证g(x)在(0,+∞)有零点.

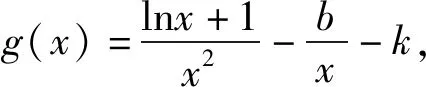
五、从充要条件退到必要条件

一般地，所解的数学问题都是充要问题，但有些问题不容易入手，求解时不妨放宽条件，先求其必要条件，对于取值范围问题而言，就是先缩小范围，这样有助于对问题的处理.

例5 若a>0，x2+ax+4<0有唯一整数解，求实数a的取值范围.

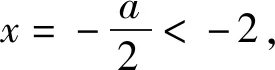
评注：还可以先从端点考虑，也称端点效应，从而缩小所求参数的范围，例如函数f(x)=x2-2ax+1在区间[1,2]上恒成立，求参数a的取值范围问题，可以先考虑端点，f(1)≥0,f(2)≥0从而缩小范围，得a≤1，得到二次函数的对称轴小于等于1，函数f(x)在区间[1,2]单调的，从而解决问题.

总之，深度学习能矫正学生浅层次的学习，更强调学生在学习过程中的理解程度与思考程度，从而达到更高阶的思维程度.