让学生看到数学森林一片
2022-08-09江苏省苏州市陆慕高级中学215131万福昌
江苏省苏州市陆慕高级中学 (215131) 万福昌
1 问题提出
《普通高中数学课程标准》(2017年版)中提出:“提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界”,会用数学的眼光观察世界,其中所指的这个世界也应包含数学.
教学中,一方面鼓励学生用数学的眼光看现实生活;另一方面,也要积极鼓励学生用数学的眼光看数学.我们面对数学对象或问题,如何让学生用数学的眼光看数学?如何让学生看到更多的数学背景,并在观察、联想、思考的过程中发展学生的能力和素养?
笔者在一次公开课上尝试用一个数学问题,鼓励学生联想已学习的数学知识,多角度思考解决问题的途径.课堂教学设计旨在探究如何让学生看到数学森林一片,公开课得到了听课者好评,惊叹学生的联想能力和思维发散度.下面录入课堂教学主要片断,与同行们分享教学中的体会.
2 案例

视角一:视为和积式
师:这个题目是我们所熟知的简单题,请根据已知条件和结论中的式子特征联想有关数学知识,并加以解决.
生1:已知为和、所求为积,联想基本不等式.
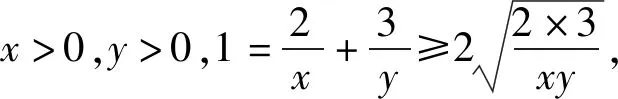
视角二:视为三角函数平方关系
师:你能联想到三角有关知识吗?
生2:联想到公式sin2θ+cos2θ=1.

师:同样地,也可以联想圆的方程或椭圆方程.
视角三:视为等差数列
师:你能联想到数列有关知识吗?
生3:联想等差数列中项.

视角四:视为平面几何图形中有关量.
师:能否联想有关几何图形?
生4:构造直角三角形,运用几何或三角知识来解决问题.
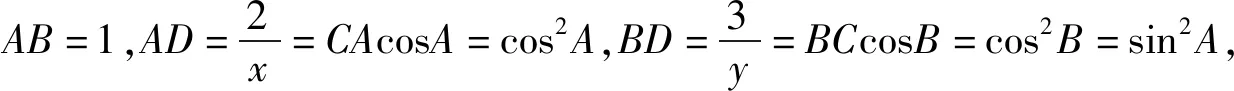
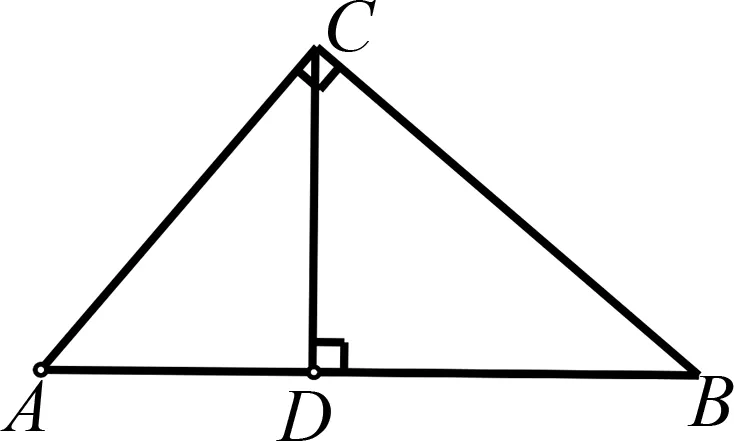
图1

视角五:视为直线方程
师:有哪些式子和为1,能利用相关知识来解决吗?

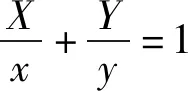
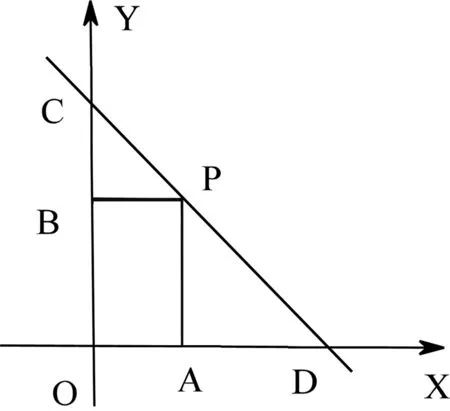
图2
生6说出了下列解法8.
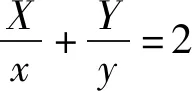

视角六:视为函数求值域
师:求变量的范围,还有什么方法?
生7:将xy消元变为一元函数求值域.


视角七:视为方程的根
师:从方程的视角看,两个数的和可以联想到什么?
生8:联想到一元二次方程根与系数的关系,可构造一元二次方程.
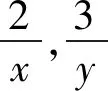
视角八:视为方程的系数
师:在求解二元变量时,除了消元变为一元函数,还可以考虑整体设元,回带求解.
生9提供了解法13.
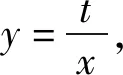
师:整体设元,回代后视为一元二次方程的系数,再用判别式求范围.
视角九:视为线性规划问题
师:在求线性规划中,我们如何求范围.
生10:将目标函数视为整体,变为函数和可行域有公共交点.
视角十:视为工程应用问题
师:还能联想到什么数学问题?
生11:联想到应用问题中的工程问题:一项工作,若甲、乙单独完成分别为x,y小时完成,若甲单独做2个小时,乙再做3个小时,恰好完成工作,求xy的最小值.

师:解法15将问题特殊化,虽然解法不严谨,但敢于联想,联想到应用问题中的工程问题还是值得肯定.
3 教学思考
师生共同探究下,学生通过联想激活思维,对问题“横看成岭侧成峰”,使这节变成了一堂智趣的数学课.一个简单的问题,可以用十种不同的视角,十多种不同的方法来解决,几乎涵盖了函数、导数、三角、数列、不等式、平面几何、解析几何、方程等数学的主干知识.教学后有如下体会.
3.1 让学生看到数学的森林一片
数学发展的动力,一方面来源于生活实际需要,另一方面是数学自身发展的需要.从数学的发现和创造过程来看,数的产生和发展不只是实际需求的结果,也是数学内部矛盾作用的结果.正负数不仅起源于为了表示具有相反意义的量,也是数学自身发展的需要.无理数的产生也是如此.教学实践中既要强调用数学的眼光看客观世界,也要用数学的眼光数学.
在不同的视角中,建立数学知识之间的联系,灵活运用数学知识解决问题,积极发展学生的思维发散力,培养学生的数学思想方法运用意识,培育数学的关键能力.
3.2 数学联想让学生思维翩翩起舞
联想是一种自觉的有目的的想象,是由当前感知或思考的事物,想起有关的另一种事件,或由此再想起其他事件的心理活动,丰富多彩的想象,往往有利于开拓思路.只要善于想象,精心联想,就能做到灵活解题.
在教学中,教师要善于鼓励学生多角度的审视已知条件、结论,把握数学的本质特征,充分联想有关数学知识,着力培养学生的发散思维的习惯.
联想需要数学知识做基础.如|x|=1,在数轴上看是两个点,在平面直角坐标系中看是两条直线,在复平面中是一个圆,在空间直角坐标系中是个球面.掌握数学概念本质,数学公式的特征十分必要,是数学运用的前提,也是数学联想活动的关键.联想思维的方式,主要有相似联想、数形联想、化归联想、整体联想.在数学解题过程中,要针对数学问题的内容和特点展开联想,由于联想的方式以及方向、角度不同,往往可以得出多种解法.而相似联想、数形联想、化归联想、整体联想在解题中并不是独立的,在同一题目中可以相互交错使用.
在数学教学中,培养学生既会用数学的眼光看世界,也会用数学的眼光看数学.面对数学问题,鼓励学生充分联想,多视角审视数学对象,让学生看到数学森林一片.
