齐次线性方程组解的结构问题的教学设计

裴慧敏 （江苏师范大学 数学与统计学院，江苏 徐州 221116）

1 引 言

在中学数学中，对于给定的线性方程组，一般只需要求出它的解即可，这对于线性方程组的研究是远远不够的.对于给定的线性方程组，它可能无解、有唯一解或者有无穷多解.当线性方程组无解或者有唯一解的时候，都很容易表示出来.但是，当线性方程组有无穷多解的时候，不可能将所有的解都一一表示出来.那么，如何将这无穷多解以一种比较简洁的形式表示出来呢？

本文主要是关于齐次线性方程组解的结构问题的教学设计.首先，通过问题引入，引出齐次线性方程组的解的结构问题.再通过不断引导学生，给出基础解系、结构式通解的相关概念.最后，给出求结构式通解的方法.本文结尾，也结合本节课知识点，融合课堂思政，做到教书育人相结合.

2 教学过程

2.1 问题引入

首先，我们来回顾一下，对于给定的齐次线性方程组，如何求出它的解.

解齐次线性方程组

则齐次线性方程组（2.1）可以表示成矩阵形式

其中，就是要求的齐次线性方程组的解.

通过前面的学习我们知道，要求，首先就要对方程组的系数矩阵施行初等行变换将其化为行最简形矩阵：

显然，（）＝2＜5，所以，原齐次线性方程组有无穷多个解，其通解为

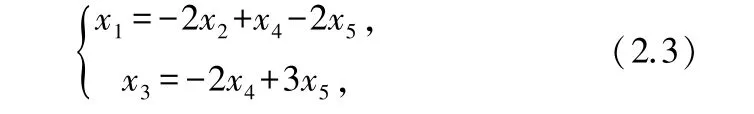
其中，，是自由未知量.

把自由未知量，，依次取为任意常数，，，则方程组＝0 的通解还可表示为

显然，当未知量的个数比较多且自由未知量的个数比较少时，如果继续用（2.4）式来表示齐次线性方程组＝0 的解，就会比较烦琐.

对于一般的齐次线性方程组＝0，当它有无穷多解时，如何以一种比较简洁的形式将这无穷多解表示出来呢？这一问题值得我们去研究，这就是齐次线性方程组解的结构问题.

2.2 研究问题

给定元齐次线性方程组

则齐次线性方程组（2.5）可以表示成矩阵形式

其中，是系数矩阵，是齐次线性方程组（2.6）的一个解向量或者解.

注意到，当齐次线性方程组＝0 有无穷多解时，它的所有解向量就可以组成一个集合，记为解集那么，根据向量组的极大无关组的定义，如果我们能够找到解集的极大无关组，那么，解集中的任何一个解向量都可以由该极大无关组线性表示，即齐次线性方程组＝0 的无穷多解可以由该极大无关组线性表示.

将解集的极大无关组记为，，…，α，显然，它需要满足如下三个条件：

（1），，…，α是解集的一个部分组；

（2），，…，α线性无关；

（3）解集中的任一向量都可由，，…，α线性表示.

对于这个极大无关组，我们将它称为齐次线性方程组＝0 的基础解系.下面，我们具体给出基础解系的概念.

定义2.1齐次线性方程组＝0 的一组解，，…，α称为它的一个基础解系，如果

（1），，…，α线性无关；

（2）方程组＝0 的任一解都可由，，…，α线性表示.

显然，如果，，…，α是方程组＝0 的一个基础解系，那么方程组＝0 的任意一个解都可以表示成如下形式：

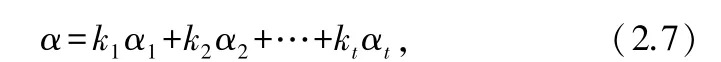
其中，，…，k是一组常数.反之，对于任意一组数，，…，k，也都是方程组＝0 的一个解，因为

我们将式（2.7）称为齐次线性方程组＝0 的结构式通解.

对于一般的齐次线性方程组＝0，当它有无穷多解时，我们就可以用结构式通解将它的无穷多解简洁地表示出来.那么，对于给定的齐次线性方程组＝0，如何求出它的结构式通解呢？

要求齐次线性方程组＝0 的结构式通解，首先就要求出它的基础解系.根据基础解系的定义，我们思考：

（1）什么样的齐次线性方程组＝0 存在基础解系？

（2）若存在，如何求出齐次线性方程组＝0 的基础解系？

下面，我们将围绕这两个问题进行讨论.

首先，我们来看第一个问题.

由前面的学习，我们知道只含零向量的向量组不存在极大无关组，也就是说，只有当齐次线性方程组＝0 有非零解（无穷解）时，即（）＜时，它才存在基础解系.

接下来，我们从秩的角度出发，对第二个问题进行研究.

设（）＝，的行最简形矩阵为

当＝0 时，为零矩阵，即＝0.此时，任一维列向量都是方程组＝0 的解.由于＝0 与＝0 同解，所以，任一维列向量都是方程组＝0 的解.也就是说，＝0 的解集是由所有的维列向量构成的.通过前面的学习知道，维单位向量组，，…，ε是解集的一个极大无关组，所以，任意个线性无关的维列向量都是方程组＝0 的一个基础解系.

当0＜＜时，不妨设的前个列向量线性无关，由于的列向量组与的列向量组具有完全相同的线性关系，所以，矩阵可设为

则方程组＝0 的通解可表示为

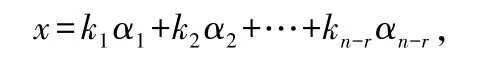
即＝0 的任一解都可由，，…，α线性表示.

如果，，…，α又是方程组＝0 的-个线性无关的解，那么，，，…，α就是方程组＝0 的基础解系.接下来，我们只需证，，…，α是方程组＝0 的-个线性无关的解即可.

通过观察我们发现：在方程组＝0 的通解（2.8）中把自由未知量x，x，…，x依次取-组值：

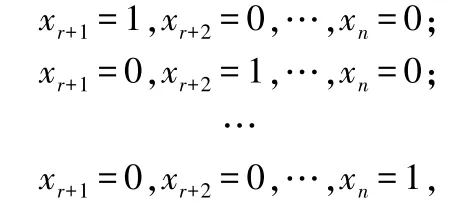
就得到了，，…，α，也就是说，，…，α是方程组＝0 的-个解.

接下来，我们只需证明，，…，α线性无关即可.为此，建立向量方程

解得＝＝…＝t＝0，也就是，，…，α线性无关.结合上述分析可得，，，…，α是方程组＝0 的基础解系.

进而，可以得到下面的定理：

设是×矩阵，若齐次线性方程组＝0 有非零解，即（）＜，则它的基础解系存在，且基础解系所含的向量个数等于-（）.

上述分析还给出了求基础解系的方法：

第1 步 用初等行变换把系数矩阵化成行最简形矩阵.

第2 步 写出方程组＝0 的通解，然后在通解中把自由未知量x，x，…，x依次取-组值：

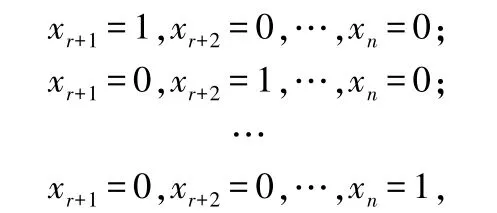
就可得到方程组＝0 的-个线性无关的解，，…，α，也就是＝0 的一个基础解系.

第3 步 写出齐次线性方程组＝0 的结构式通解：

其中，，…，k为任意常数.

下面，我们通过例题来看一下具体如何求出齐次线性方程组的结构式通解.

求齐次线性方程组的结构式通解.

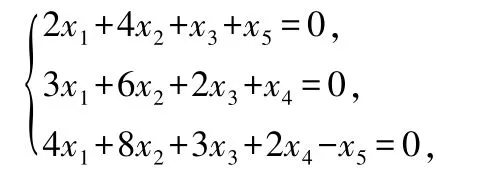
要想得到齐次线性方程组的结构式通解，首先就要求出它的基础解系.

由2.1 节可知，齐次线性方程组的通解为

其中，，是自由未知量.

则，，是原方程组的一个基础解系，所以原方程组的结构式通解为

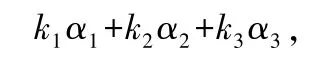
其中，，为任意常数.

课后思考：齐次线性方程组＝0 可以看成是一种比较简单的线性方程组.那么，对于一般的线性方程组＝，当它有无穷多解时，如何求出它的结构式通解呢？容易看出，当一般的线性方程组＝有无穷多个解时，与其对应的齐次线性方程组＝0 也有无穷多个解.那么，可否借用齐次线性方程组＝0 的基础解系给出＝的结构式通解呢？这个问题，我们将在下节课与大家一起探讨.

2.3 内容小结

本次课程通过具体的例子引入了基础解系的概念.并在此基础上，引导学生得到了结构式通解的概念.然后，从秩的角度出发，得到了基础解系的求解方法，进而得到了齐次线性方程组的结构式通解.最后，结合具体的例题，给出了求解齐次线性方程组的结构式通解的方法.本次课程从简单问题入手，通过一步步引导学生，结合学生之前所学知识一步步达到教学目的.这种教学设计思路，不仅能够吸引学生的注意力，提高他们的学习兴趣，而且还能引发他们的思考，培养他们发现问题、分析问题和解决问题的能力.

3 课堂思政

本次课程我们主要学习了齐次线性方程组的基础解系，借助基础解系，我们研究了齐次线性方程组的结构式通解.通过本节课的学习，我们能够发现，结构式通解能够使齐次线性方程组的解的表示变得更加简洁优美.数学中有解的结构，我们在人生的道路上能否取得成功也有解的结构，伟大的科学家爱迪生说过：“成功等于1%的灵感加99%的汗水.”99%的汗水能够使我们的人生变得更加完美.所以，不管是在求学过程中，还是在以后的工作中，想要成功就要付出努力.只要坚定信心，勇往直前，就终将会实现人生理想和目标.